Article contents
Encoder–decoder neural network for solving the nonlinear Fokker–Planck–Landau collision operator in XGC
Published online by Cambridge University Press: 24 March 2021
Abstract
An encoder–decoder neural network has been used to examine the possibility for acceleration of a partial integro-differential equation, the Fokker–Planck–Landau collision operator. This is part of the governing equation in the massively parallel particle-in-cell code XGC, which is used to study turbulence in fusion energy devices. The neural network emphasizes physics-inspired learning, where it is taught to respect physical conservation constraints of the collision operator by including them in the training loss, along with the 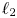 $\ell _2$ loss. In particular, network architectures used for the computer vision task of semantic segmentation have been used for training. A penalization method is used to enforce the ‘soft’ constraints of the system and integrate error in the conservation properties into the loss function. During training, quantities representing the particle density, momentum and energy for all species of the system are calculated at each configuration vertex, mirroring the procedure in XGC. This simple training has produced a median relative loss, across configuration space, of the order of
$\ell _2$ loss. In particular, network architectures used for the computer vision task of semantic segmentation have been used for training. A penalization method is used to enforce the ‘soft’ constraints of the system and integrate error in the conservation properties into the loss function. During training, quantities representing the particle density, momentum and energy for all species of the system are calculated at each configuration vertex, mirroring the procedure in XGC. This simple training has produced a median relative loss, across configuration space, of the order of 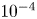 $10^{-4}$, which is low enough if the error is of random nature, but not if it is of drift nature in time steps. The run time for the current Picard iterative solver of the operator is
$10^{-4}$, which is low enough if the error is of random nature, but not if it is of drift nature in time steps. The run time for the current Picard iterative solver of the operator is 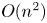 $O(n^2)$, where
$O(n^2)$, where 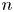 $n$ is the number of plasma species. As the XGC1 code begins to attack problems including a larger number of species, the collision operator will become expensive computationally, making the neural network solver even more important, especially since its training only scales as
$n$ is the number of plasma species. As the XGC1 code begins to attack problems including a larger number of species, the collision operator will become expensive computationally, making the neural network solver even more important, especially since its training only scales as 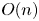 $O(n)$. A wide enough range of collisionality has been considered in the training data to ensure the full domain of collision physics is captured. An advanced technique to decrease the losses further will be subject of a subsequent report. Eventual work will include expansion of the network to include multiple plasma species.
$O(n)$. A wide enough range of collisionality has been considered in the training data to ensure the full domain of collision physics is captured. An advanced technique to decrease the losses further will be subject of a subsequent report. Eventual work will include expansion of the network to include multiple plasma species.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press
References
- 12
- Cited by


