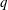Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T23:13:09.212Z Has data issue: false hasContentIssue false
  • English
  • Français

Transverse instability of ion acoustic solitons in a magnetized plasma including $q$ -nonextensive electrons and positrons

Published online by Cambridge University Press:  04 September 2015

N. Akhtar ,
W. F. El-Taibany ,
S. Mahmood ,
E. E. Behery ,
S. A. Khan ,
S. Ali  and
S. Hussain
N. Akhtar*
Affiliation:
Theoretical Physics Division (TPD), PINSTECH P.O. Nilore, Islamabad 44000, Pakistan Department of Physics and Applied Mathematics (DPAM), PIEAS P.O. Nilore, Islamabad 44000, Pakistan
W. F. El-Taibany
Affiliation:
Department of Physics, Faculty of Science, Damietta University, New Damietta, P.O. 34517, Egypt Department of Physics, College of Science for Girls in Abha, King Khalid University, P.O. 960, Abha, Kingdom of Saudi Arabia
S. Mahmood
Affiliation:
Theoretical Physics Division (TPD), PINSTECH P.O. Nilore, Islamabad 44000, Pakistan Department of Physics and Applied Mathematics (DPAM), PIEAS P.O. Nilore, Islamabad 44000, Pakistan National Centre for Physics (NCP), Quaid-i-Azam University Campus, Shahdra Valley Road, Islamabad 44000, Pakistan
E. E. Behery
Affiliation:
Department of Physics, Faculty of Science, Damietta University, New Damietta, P.O. 34517, Egypt
S. A. Khan
Affiliation:
National Centre for Physics (NCP), Quaid-i-Azam University Campus, Shahdra Valley Road, Islamabad 44000, Pakistan
S. Ali
Affiliation:
National Centre for Physics (NCP), Quaid-i-Azam University Campus, Shahdra Valley Road, Islamabad 44000, Pakistan
S. Hussain
Affiliation:
Theoretical Physics Division (TPD), PINSTECH P.O. Nilore, Islamabad 44000, Pakistan Department of Physics and Applied Mathematics (DPAM), PIEAS P.O. Nilore, Islamabad 44000, Pakistan
*
†Email addresses for correspondence: naseemqau@gmail.com, naseem_qau@yahoo.com
Get access Rights & Permissions [Opens in a new window]

Abstract

A nonlinear Zakharov–Kuznetsov (ZK) equation for ion acoustic solitary waves (IASWs) is derived using the reductive perturbation method (RPM) for magnetized plasmas in which the inertialess electrons and positrons are nonextensively 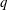$q$ -distributed while ions are assumed to be warm and inertial. It is found that both compressive as well as rarefactive solitons coexist in the present model for different regions of non-extensive electron and positron parameters, 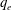$q_{e}$ and 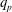$q_{p}$ . The magnetic field has no effect on the amplitude of the IASW, whereas the obliqueness angle of the wave propagation, the ion-to-electron temperature ratio  ${\it\sigma}$ and positron-to-ion density concentration ratio 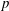$p$ affect both the amplitude and the width of the solitary wave structures. The transverse instability analysis illustrates that the one soliton solution has a constant growth rate, and it suffers from instability in the transverse direction. The relevance of the present study to astrophysical space plasmas is also discussed.

Type
Research Article
Information
Journal of Plasma Physics , Volume 81 , Issue 5 , October 2015 , 905810518
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, S. & Okamoto, Y. 2001 Statistical Mechanics and its Applications. Springer.Google Scholar
Akhtar, N., El-Taibany, W. F. & Mahmood, S. 2013 Electrostatic double layers in a warm negative ion plasma with nonextensive electrons. Phys. Lett. A 377, 1282–1289.Google Scholar
Asbridge, J. R., Bame, S. J. & Strong, I. B. 1968 Outward flow of protons from the Earth’s bow shock. J. Geophys. Res. 73 (17), 5777–5782.Google Scholar
Bains, A. S., Tribeche, M., Saini, N. S. & Gill, T. S. 2011 A nonlinear Zakharov–Kuznetsov equation in magnetized plasma with $q$ -nonextensive electrons velocity distribution. Phys. Plasmas 18, 104503.1–104503.4.Google Scholar
Christon, S. P. et al. 2012 Energy spectra of plasma sheet ions and electrons from ${\sim}50~\text{eV}~\text{e}^{-1}$ to ${\sim}1~\text{MeV}$ during plasma temperature transitions. J. Geophys. Res. 93, 2562–2572.Google Scholar
Das, K. P. & Verheest, F. 1989 Ion-acoustic solitons in magnetized multi-component plasmas including negative ions. J. Plasma Phys. 41, 139–155.Google Scholar
Divine, N. & Garret, H. B. 1983 Charged particle distributions in Jupiter’s magnetosphere. J. Geophys. Res. 88, 6889–6903.Google Scholar
Dodd, R. K. et al. 1982 Solitons and Nonlinear Waves Equations. Academic.Google Scholar
Du, J. 2004 Nonextensivity in nonequilibrium plasma systems with Coulombian long-range interactions. Phys. Lett. A 329, 262–267.Google Scholar
El-Taibany, W. F., El-Bedwehy, N. A. & El-Shamy, E. F. 2011 Three-dimensional stability of dust-ion acoustic solitary waves in a magnetized multicomponent dusty plasma with negative ions. Phys. Plasmas 18, 033703.1–033703.8.Google Scholar
El-Taibany, W. F. & Tribeche, M. 2012 Nonlinear ion-acoustic solitary waves in electronegative plasmas with electrons featuring Tsallis distribution. Phys. Plasmas 19, 024507.1–024507.4.Google Scholar
Futaana, Y. et al. 2003 Moon-related nonthermal ions observed by Nozomi: species, sources, and generation mechanisms. J. Geophys. Res. 108, 15.1–15.10.Google Scholar
Ghosh, S. & Chakrabart, N. 2013 Magnetic electron drift solitons in electron magnetohydrodynamic plasmas. Plasma Phys. Control. Fusion 55, 035008.1–035008.4.Google Scholar
Ghosh, U. N., Chatterjee, P. & Roychoudhury, R. 2012 The effect of $q$ -distributed electrons on the head-on collision of ion acoustic solitary waves. Phys. Plasmas 19, 012113.1–012113.6.Google Scholar
Gosset, W. 1908 The probable error of a mean. Biometrika 6, 1–25.Google Scholar
Haque, Q., Mahmood, S. & Mushtaq, A. 2008 Nonlinear electrostatic drift waves in dense electron–positron–ion plasmas. Phys. Plasmas 15, 082315.1–082315.5.Google Scholar
Hellberg, M. A. et al. 2009 Comment on ‘Mathematical and physical aspects of Kappa velocity distribution’ [Phys. Plasmas 14, 110702 2007]. Phys. Plasmas 16, 094701.1–094701.5.Google Scholar
Hirotani, K. et al. 1999 Pair plasma dominance in the 3c 279 jet on parsec scales. Publ. Astron. Soc. Japan 51 (2), 263–267.Google Scholar
Hussain, S., Akhtar, N. & Mahmood, S. 2013 Propagation of ion acoustic shock waves in negative ion plasmas with nonextensive electrons. Phys. Plasmas 20, 092303.1–092303.7.Google Scholar
Iwamoto, N. 1993 Collective modes in nonrelativistic electron–positron plasmas. Phys. Rev. E 47, 604–611.Google Scholar
Jain, S. L., Tiwari, R. S. & Sharma, S. R. 1990 Large-amplitude ion-acoustic double layers in multispecies plasma. Can. J. Phys. 68, 474–478.Google Scholar
Kourakis, I. et al. 2009 Nonlinear dynamics of rotating multi-component pair plasmas and epi plasmas. Plasma Fusion Res. 4, 018.1–018.11.Google Scholar
Latora, V., Rapisarda, A. & Tsallis, C. 2001 Non-Gaussian equilibrium in a long-range Hamiltonian system. Phys. Rev. E 64, 056134.1–056134.5.Google Scholar
Lazarus, I. J. et al. 2012a Arbitrary amplitude Langmuir solitons in a relativistic electron–positron plasma. J. Plasma Phys. 78 (2), 175–180.Google Scholar
Lazarus, I. J. et al. 2012b Linear electrostatic waves in two-temperature electron–positron plasmas. J. Plasma Phys. 78 (6), 621–628.Google Scholar
Leubner, M. P. 2004 Fundamental issues on kappa-distributions in space plasmas and interplanetary proton distributions. Phys. Plasmas 11, 1308–1316.CrossRefGoogle Scholar
Lima, J. A. S., Silva, J. R. & Santos, J. 2000 Plasma oscillations and nonextensive statistics. Phys. Rev. E 61, 3260–3263.Google Scholar
Liu, J. M. et al. 1994 Measurements of inverse bremsstrahlung absorption and non-Maxwellian electron velocity distributions. Phys. Rev. Lett. 72 (17), 2717–2720.Google Scholar
Liyan, L. & Jiulin, D. 2008 Ion acoustic waves in the plasma with the power-law $q$ -distribution in nonextensive statistics. Physica A 387, 4821–4827.Google Scholar
Lonngren, K. E. 1998 Ion acoustic soliton experiments in a plasma. Opt. Quant. Electron. 30, 615–630.Google Scholar
Mace, R. L. & Hellberg, M. A. 2001 The Korteweg–de Vries–Zakharov–Kuznetsov equation for electron-acoustic waves. Phys. Plasmas 8, 2649–2656.Google Scholar
Mahajan, S. M., Berezhiani, V. I. & Mikilaszewski, R. 1998 On the robustness of the localized spatiotemporal structures in electron–positron–ion plasmas. Phys. Plasmas 5, 3264–3269.CrossRefGoogle Scholar
Mahmood, S. & Akhtar, N. 2008 Ion acoustic solitary waves with adiabatic ions in magnetized electron–positron–ion plasmas. Eur. Phys. J. D 49, 217–222.CrossRefGoogle Scholar
Mahmood, S., Akhtar, N. & Ur-Rehman, H. 2011 Acoustic solitons in magnetized quantum electron–positron plasmas. Phys. Scr. 83, 035505–035510.Google Scholar
Mahmood, S., Mushtaq, A. & Saleem, H. 2003 Ion acoustic solitary wave in homogeneous magnetized electron–positron–ion plasmas. New J. Phys. 5, 28.1–28.10.Google Scholar
Mahmood, S. & Ur-Rehman, H. 2009 Electrostatic solitons in unmagnetized hot electron–positron–ion plasmas. Phys. Lett. A 373, 2255–2259.Google Scholar
Maksimovic, M., Pierrard, V. & Riley, P. 1997 Ulysses electron distributions fitted with kappa functions. Geophys. Res. Lett. 24, 1511–1519.Google Scholar
Miller, H. R. & Wiita, P. J. 1987 Active Galactic Nuclei. Springer.Google Scholar
Moslem, W. M. et al. 2007 Solitary, explosive, and periodic solutions of the quantum Zakharov–Kuznetsov equation and its transverse instability. Phys. Plasmas 14, 082308.1–082308.5.Google Scholar
Munoz, V. 2006 A nonextensive statistics approach for Langmuir waves in relativistic plasmas. Nonlinear Process. Geophys. 13, 237–241.CrossRefGoogle Scholar
Mushtaq, A., Saeed, R. & Haque, Q. 2009 Ion acoustic solitary waves in magnetized pair-ion electron plasmas. Phys. Plasmas 16, 084501.1–084501.4.Google Scholar
Nakamura, Y. 1982 Experiments on ion-acoustic solitons in plasmas invited review article. IEEE Trans. Plasma Sci. 10, 180–195.Google Scholar
Nsengiyumva, F. et al. 2014 Stopbands in the existence domains of acoustic solitons. Phys. Plasmas 21 (10), 102301.1–102301.8.Google Scholar
Pakzad, H. R. & Tribeche, M. 2011 Electron acoustic double layers in a plasma with a $q$ -nonextensive electron velocity distribution. Astrophys. Space Sci. 334, 45–53.Google Scholar
Popel, S. I., Vladimirov, S. V. & Shukla, P. K. 1995 Ion-acoustic solitons in electron–positron–ion plasmas. Phys. Plasmas 2 (3), 716–719.Google Scholar
Renyi, A. 1955 On a new axiomatic theory of probability. Acta Math. Acad. Sci. Hung. 6, 285–335.Google Scholar
Reynolds, C. S. et al. 1996 The matter content of the jet in M87: evidence for an electron–positron jet. Mon. Not. R. Astron. Soc. 283, 873–880.Google Scholar
Sahu, B. 2011 Ion acoustic solitary waves and double layers with nonextensive electrons and thermal positrons. Phys. Plasmas 18, 082302.1–082302.6.Google Scholar
Saini, N. S. & Kholi, R. 2014 Electrostatic envelope excitations under transverse perturbations in a plasma with nonextensive hot electrons. Astrophys. Space Sci. 349, 293–303.CrossRefGoogle Scholar
Saini, N. S. & Shalini 2013 Ion acoustic solitons in a nonextensive plasma with multi-temperature electrons. Astrophys. Space Sci. 346, 155–163.Google Scholar
Saitou, Y. & Nakamura, Y. 2005 Ion-acoustic soliton-like waves undergoing Landau damping. Phys. Lett. A 343, 397–402.Google Scholar
Samanta, U. K., Saha, A. & Chatterjee, P. 2013 Bifurcations of nonlinear ion acoustic travelling waves in the frame of a Zakharov–Kuznetsov equation in magnetized plasma with a kappa distributed electron. Phys. Plasmas 20, 052111.1–052111.5.Google Scholar
Shan, S. A. & Akhtar, N. 2013 Korteweg–de Vries equation for ion acoustic soliton with negative ions in the presence of nonextensive electrons. Astrophys. Space Sci. 346, 367–374.Google Scholar
Silva, R. Jr., Plastino, A. R. & Lima, J. A. S. 1998 A Maxwellian path to the $q$ -nonextensive velocity distribution function. Phys. Lett. A 249 (5), 401–408.Google Scholar
Singh, S. V. et al. 2013 Effect of ion temperature on ion-acoustic solitary waves in a magnetized plasma in presence of superthermal electrons. Phys. Plasmas 20, 012306.1–012306.6.CrossRefGoogle Scholar
Stenflo, L., Shukla, P. K. & Yu, M. Y. 1985 Nonlinear propagation of electromagnetic waves in magnetized electron–positron plasmas. Astrophys. Space Sci. 117 (2), 303–308.Google Scholar
Sultana, S. et al. 2010 Oblique electrostatic excitations in a magnetized plasma in the presence of excess superthermal electrons. Phys. Plasmas 17, 032310.1–032310.10.Google Scholar
Taruya, A. & Sakagami, M. A. 2003 Long-term evolution of stellar self-gravitating systems away from thermal equilibrium: connection with nonextensive statistics. Phys. Rev. Lett. 90, 181101.1–181101.4.CrossRefGoogle ScholarPubMed
Tiwari, R. S., Jain, S. L. & Chawla, J. K. 2007 Ion acoustic cnoidal waves and associated nonlinear ion flux in a warm ion plasma. Phys. Plasmas 14, 022106.1–022106.9.Google Scholar
Tran, M. Q. 1979 Ion acoustic solitons in a plasma: a review of their experimental properties and related theories. Phys. Scr. 20, 317–327.Google Scholar
Tribeche, M., Djebarni, L. & Amour, R. 2010 Ion-acoustic solitary waves in a plasma with a $q$ -nonextensive electron velocity distribution. Phys. Plasmas 17, 042114.1–042114.6.Google Scholar
Tsallis, C. 1988 Possible generalization of Boltzmann–Gibbs statistics. J. Stat. Phys. 52, 479–487.Google Scholar
Tsallis, C. 1995 Non-extensive thermostatistics: brief review and comments. Physica A 221, 277–290.Google Scholar
Vasyliunas, V. M. 1968 A survey of low energy electrons in the evening sector of the magnetosphere with OGO-1 and OGO-3. J. Geophys. Res. 73, 2839–2884.Google Scholar
Verheest, F. et al. 2006 On the existence of ion-acoustic double layers in two-electron temperature plasmas. Phys. Plasmas 13, 042301.1–042301.9.Google Scholar
Verheest, F. 2013 Ambiguities in the Tsallis description of non-thermal plasma species. J. Plasma Phys. 79 (6), 1031–1034.Google Scholar
Washimi, H. & Taniuti, T. 1966 Propagation of ion-acoustic solitary waves of small amplitude. Phys. Rev. Lett. 17, 996–997.Google Scholar
Yu, M. Y., Shukla, P. K. & Stenflo, L. 1986 Alfven vortices in a strongly magnetized electron-position plasma. Astrophys. J. 309, L63–L66.Google Scholar
Zakharov, V. E. & Kuznetsov, E. A. 1974 Three-dimensional solitons. Sov. Phys. JETP 39, 285–286.Google Scholar
Zank, G. P. & Greaves, R. G. 1995 Linear and nonlinear modes in nonrelativistic electron–positron plasmas. Phys. Rev. E 51, 6079–6090.Google Scholar