No CrossRef data available.
Article contents
Characteristics of collisional damping of surface ion-acoustic mode in Divertor Plasma Simulator-2 (DiPS-2)
Published online by Cambridge University Press: 15 December 2021
Abstract
The dissipation of ion-acoustic surface waves propagating in a semi-bounded and collisional plasma which has a boundary with vacuum is theoretically investigated and this result is used for the analysis of edge-relevant plasma simulated by Divertor Plasma Simulator-2 (DiPS-2). The collisional damping of the surface wave is investigated for weakly ionized plasmas by comparing the collisionless Landau damping with the collisional damping as follows: (1) the ratio of ion temperature $({T_i})$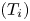 to electron temperature $({T_e})$
to electron temperature $({T_e})$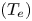 should be very small for the weak collisionality $({T_i}/{T_e} \ll 1)$
should be very small for the weak collisionality $({T_i}/{T_e} \ll 1)$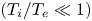 ; (2) the effect of collisionless Landau damping is dominant for the small parallel wavenumber, and the decay constant is given as $\gamma \approx{-} \sqrt {\mathrm{\pi }/2} {k_\parallel }{\lambda _{De}}\omega _{pi}^2/{\omega _{pe}}$
; (2) the effect of collisionless Landau damping is dominant for the small parallel wavenumber, and the decay constant is given as $\gamma \approx{-} \sqrt {\mathrm{\pi }/2} {k_\parallel }{\lambda _{De}}\omega _{pi}^2/{\omega _{pe}}$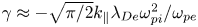 ; and (3) the collisional damping dominates for the large parallel wavenumber, and the decay constant is given as $\gamma \approx{-} {\nu _{in}}/16$
; and (3) the collisional damping dominates for the large parallel wavenumber, and the decay constant is given as $\gamma \approx{-} {\nu _{in}}/16$ , where ${\nu _{in}}$
, where ${\nu _{in}}$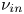 is the ion–neutral collisional frequency. An experimental simulation of the above theoretical prediction has been done in the argon plasma of DiPS-2, which has the following parameters: plasma density ${n_e} = (\textrm{2--9)} \times \textrm{1}{\textrm{0}^{11}}\;\textrm{c}{\textrm{m}^{ - 3}}$
is the ion–neutral collisional frequency. An experimental simulation of the above theoretical prediction has been done in the argon plasma of DiPS-2, which has the following parameters: plasma density ${n_e} = (\textrm{2--9)} \times \textrm{1}{\textrm{0}^{11}}\;\textrm{c}{\textrm{m}^{ - 3}}$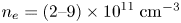 , ${T_e} = 3.7- 3.8\;\textrm{eV}$
, ${T_e} = 3.7- 3.8\;\textrm{eV}$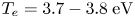 , ${T_i} = 0.2- 0.3\;\textrm{eV}$
, ${T_i} = 0.2- 0.3\;\textrm{eV}$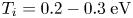 and collision frequency ${\nu _{in}} = 23- 127\;\textrm{kHz}$
and collision frequency ${\nu _{in}} = 23- 127\;\textrm{kHz}$ . Although the wavelength should be specified with the given parameters of DiPS-2, the collisional damping is found to be $\gamma = ( - 0.9\;\textrm{to}\; - 5) \times {10^4}\;\textrm{rad}\;{\textrm{s}^{ - 1}}$
. Although the wavelength should be specified with the given parameters of DiPS-2, the collisional damping is found to be $\gamma = ( - 0.9\;\textrm{to}\; - 5) \times {10^4}\;\textrm{rad}\;{\textrm{s}^{ - 1}}$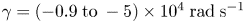 for ${k_\parallel }{\lambda _{De}} = 10$
for ${k_\parallel }{\lambda _{De}} = 10$ , while the Landau damping is found to be $\gamma = ( - 4\;\textrm{to}\; - 9) \times {10^4}\;\textrm{rad}\;{\textrm{s}^{ - 1}}$
, while the Landau damping is found to be $\gamma = ( - 4\;\textrm{to}\; - 9) \times {10^4}\;\textrm{rad}\;{\textrm{s}^{ - 1}}$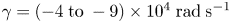 for ${k_\parallel }{\lambda _{De}} = 0.1$
for ${k_\parallel }{\lambda _{De}} = 0.1$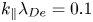 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press


