Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T04:13:55.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Covariant magnetic connection hypersurfaces

Part of: Frontiers in Plasma Physics Conference Premio Vincenzo Ferraro in Space Plasma

Published online by Cambridge University Press:  30 March 2016

F. Pegoraro
F. Pegoraro*
Affiliation:
Department of Physics, University of Pisa, largo Pontecorvo 3, 56127 Pisa, Italy
*
†Email address for correspondence: francesco.pegoraro@unipi.it
Get access Rights & Permissions [Opens in a new window]

Abstract

In the single fluid, non-relativistic, ideal magnetohydrodynamic (MHD) plasma description, magnetic field lines play a fundamental role by defining dynamically preserved ‘magnetic connections’ between plasma elements. Here we show how the concept of magnetic connection needs to be generalized in the case of a relativistic MHD description where we require covariance under arbitrary Lorentz transformations. This is performed by defining 2-D magnetic connection hypersurfaces in the 4-D Minkowski space. This generalization accounts for the loss of simultaneity between spatially separated events in different frames and is expected to provide a powerful insight into the 4-D geometry of electromagnetic fields when 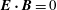$\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}=0$.

Type
Research Article
Information
Journal of Plasma Physics , Volume 82 , Issue 2 , April 2016 , 555820201
Check for updates
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anile, M. 1989 Relativistic Fluids and Magneto-Fluids, Cambridge Monographs on Mathematical Physics.Google Scholar
Asenjo, F. A. & Comisso, L. 2015 Generalized magnetofluid connections in relativistic magnetohydrodynamics. Phys. Rev. Lett. 114, 115003,1–5.Google Scholar
Asenjo, F. A., Comisso, L. & Mahajan, S. M. 2015 Generalized magnetofluid connections in pair plasmas. Phys. Plasmas 22, 122109,1–4.Google Scholar
Askaryan, G. A., Bulanov, S. V., Pegoraro, F. & Pukhov, A. M. 1995 Magnetic interaction of self-focused channels and magnetic wake excitation in high intensity laser pulses. Comments Plasma Phys. Control. Fusion 17, 35–43.Google Scholar
Berger, M. A. 1993 Energy-crossing number relations for braided magnetic fields. Phys. Rev. Lett. 70, 705–708.Google Scholar
Bulanov, S. V., Esirkepov, T. Zh., Habs, D., Pegoraro, F. & Tajima, T. 2009 Relativistic laser-matter interaction and relativistic laboratory astrophysics. Eur. Phys. J. D 55, 483–507.Google Scholar
Bulanov, S. V., Pegoraro, F. & Sakharov, A. S. 1992 Magnetic reconnection in electron magnetohydrodynamics. Phys. Fluids B 4, 2499–2508.Google Scholar
D’Avignon, E., Morrison, P. J. & Pegoraro, F. 2015 Action principle for relativistic magnetohydrodynamics. Phys. Rev. D 91, 084050,1–16.CrossRefGoogle Scholar
Gedalin, M. 1996 Covariant relativistic hydrodynamics of multispecies plasma and generalized Ohm’s law. Phys. Rev. Lett. 76, 3340–3343.Google Scholar
Hesse, M. & Zenitani, S. 2007 Dissipation in relativistic pair-plasma reconnection. Phys. Plasmas 14, 112102,1–8.CrossRefGoogle Scholar
Koide, S. 2010 Generalized general relativistic magnetohydrodynamic equations and distinctive plasma dynamics around rotating black holes. Astrophys. J. 708, 1459–1474.Google Scholar
Lichnerowicz, A. 1967 Relativistic Hydrodynamics and Magnetohydrodynamics. Benjamin.Google Scholar
Mignone, A. & Bodo, G. 2006 An HLLC Riemann solver for relativistic flows – II. Magnetohydrodynamics. Mon. Not. R. Astron. Soc. 368, 1040–1054.Google Scholar
Newcomb, W. A. 1958 Motion of magnetic lines of force. Ann. Phys. 3, 347–385.CrossRefGoogle Scholar
Nilson, P. M., Willingale, L., Kaluza, M. C., Kamperidis, C., Minardi, S., Wei, M. S., Fernandes, P., Notley, M., Bandyopadhyay, S., Sherlock, M. et al. 2006 Magnetic reconnection and plasma dynamics in two-beam laser–solid interactions. Phys. Rev. Lett. 97, 255001,1–4.Google Scholar
Pegoraro, F. 2012 Covariant form of the ideal magnetohydrodynamic ‘connection theorem’ in a relativistic plasma. Europhys. Lett. 99, 35001,1–3.Google Scholar
Pegoraro, F. 2015 Generalised relativistic Ohm’s laws, extended gauge transformations, and magnetic linking. Phys. Plasmas 22, 112106,1–6.Google Scholar
Tavani, M., Bulgarelli, A., Vittorini, V., Pellizzoni, A., Striani, E., Caraveo, P., Weisskopf, M. C., Tennant, A., Pucella, G., Trois, A. et al. 2011 Discovery of powerful gamma-ray flares from the Crab Nebula. Science 331, 736–739.CrossRefGoogle ScholarPubMed
Zenitani, S. & Hoshino, M. 2007 Particle acceleration and magnetic dissipation in relativistic current sheet of pair plasmas. Astrophys. J. 670, 702–726.Google Scholar