Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T13:57:05.741Z Has data issue: false hasContentIssue false
  • English
  • Français

The decay of isotropic magnetohydrodynamics turbulence and the effects of cross-helicity

Published online by Cambridge University Press:  05 February 2018

Antoine Briard Open the ORCID record for Antoine Briard [Opens in a new window]  and
Thomas Gomez Open the ORCID record for Thomas Gomez [Opens in a new window]
Antoine Briard*
Affiliation:
∂’Alembert, CNRS UMR 7190, 4 Place Jussieu, F-75252 Paris CEDEX 5, France Aix Marseille Université, CNRS, Centrale Marseille, M2P2 UMR 7340, 13451 Marseille, France
Thomas Gomez
Affiliation:
USTL, LML, F-59650 Villeneuve d’Ascq, France
*
†Email address for correspondence: antoine.briard92@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Decaying homogeneous and isotropic magnetohydrodynamics (MHD) turbulence is investigated numerically at large Reynolds numbers thanks to the eddy-damped quasi-normal Markovian (EDQNM) approximation. Without any background mean magnetic field, the total energy spectrum 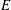$E$ scales as 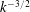$k^{-3/2}$ in the inertial range as a consequence of the modelling. Moreover, the total energy is shown, both analytically and numerically, to decay at the same rate as kinetic energy in hydrodynamic isotropic turbulence: this differs from a previous prediction, and thus physical arguments are proposed to reconcile both results. Afterwards, the MHD turbulence is made imbalanced by an initial non-zero cross-helicity. A spectral modelling is developed for the velocity–magnetic correlation in a general homogeneous framework, which reveals that cross-helicity can contain subtle anisotropic effects. In the inertial range, as the Reynolds number increases, the slope of the cross-helical spectrum becomes closer to 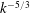$k^{-5/3}$ than 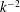$k^{-2}$ . Furthermore, the Elsässer spectra deviate from 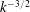$k^{-3/2}$ with cross-helicity at large Reynolds numbers. Regarding the pressure spectrum 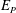$E_{P}$ , its kinetic and magnetic parts are found to scale with 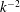$k^{-2}$ in the inertial range, whereas the part due to cross-helicity rather scales in 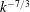$k^{-7/3}$ . Finally, the two 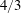$4/3$ rd laws for the total energy and cross-helicity are assessed numerically at large Reynolds numbers.

Keywords

plasma dynamicsplasma nonlinear phenomenaplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 1 , February 2018 , 905840110
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A. 2013 Large-scale magnetic fields in magnetohydrodynamic turbulence. Phys. Rev. Lett. 110 (8), 084502.CrossRefGoogle ScholarPubMed
Alexakis, A., Mininni, P. D. & Pouquet, A. 2005 Shell-to-shell energy transfer in magnetohydrodynamics. I. Steady state turbulence. Phys. Rev. E 72, 046301.CrossRefGoogle ScholarPubMed
André, J. C. & Lesieur, M. 1977 Influence of helicity on the evolution of isotropic turbulence at high Reynolds number. J. Fluid Mech. 81, 187–207.CrossRefGoogle Scholar
Baerenzung, J., Politano, H., Ponty, Y. & Pouquet, A. 2008 Spectral modeling of magnetohydrodynamic turbulent flows. Phys. Rev. E 78 (5), 026310.Google ScholarPubMed
Banerjee, R. & Jedamzik, K. 2004 Evolution of cosmic magnetic fields: from the very early universe, to recombination, to the present. Phys. Rev. D 70, 123003.Google Scholar
Batchelor, G. K. 1950 On the spontaneous magnetic field in a conducting liquid in turbulent motion. Proc. R. Soc. Lond. A 201 (1066), 405–416.Google Scholar
Beresnyak, A. 2011 Spectral slope and kolmogorov constant of MHD turbulence. Phys. Rev. Lett. 106 (7), 075001.CrossRefGoogle ScholarPubMed
Beresnyak, A. 2014 Spectra of strong magnetohydrodynamic turbulence from high-resolution simulations. Astrophys. J. Lett. 784 (2), L20.CrossRefGoogle Scholar
Beresnyak, A. & Lazarian, A. 2008 Strong imbalanced turbulence. Astrophys. J. 682 (2), 1070.CrossRefGoogle Scholar
Betchov, R. 1963 A simplified theory of magnetohydrodynamic isotropic turbulence. J. Fluid Mech. 17, 33–51.CrossRefGoogle Scholar
Biskamp, D. 2003 Magnetohydrodynamic Turbulence. Cambridge University Press.CrossRefGoogle Scholar
Biskamp, D. & Welter, H. 1989 Dynamics of decaying two-dimensional magnetohydrodynamic turbulence. Phys. Fluids B 1 (10), 1964–1979.CrossRefGoogle Scholar
Boldyrev, S. 2006 Spectrum of magnetohydrodynamic turbulence. Phys. Rev. Lett. 96 (11), 115002.CrossRefGoogle ScholarPubMed
Boldyrev, S. & Perez, J. C. 2009 Spectrum of weak magnetohydrodynamic turbulence. Phys. Rev. Lett. 103, 225001.CrossRefGoogle ScholarPubMed
Boldyrev, S., Perez, J. C., Borovsky, J. E. & Podesta, J. J. 2011 Spectral scaling laws in magnetohydrodynamics turbulence simulations and in the solar wind. Astrophys. J. Lett. 741 (1), L19.CrossRefGoogle Scholar
Briard, A. & Gomez, T. 2017 Dynamics of helicity in homogeneous skew-isotropic turbulence. J. Fluid Mech. 821, 539–581.CrossRefGoogle Scholar
Briard, A., Gomez, T. & Cambon, C. 2016 Spectral modelling for passive scalar dynamics in homogeneous anisotropic turbulence. J. Fluid Mech. 799, 159–199.CrossRefGoogle Scholar
Briard, A., Gomez, T., Sagaut, P. & Memari, S. 2015 Passive scalar decay laws in isotropic turbulence: Prandtl effects. J. Fluid Mech. 784, 274–303.CrossRefGoogle Scholar
Briard, A., Iyer, M. & Gomez, T. 2017 Anisotropic spectral modeling for unstably stratified homogeneous turbulence. Phys. Rev. Fluids 2 (4). doi:10.1103/PhysRevFluids.2.044604.CrossRefGoogle Scholar
Cambon, C. & Jacquin, L. 1989 Spectral approach to non-isotropic turbulence subjected to rotation. J. Fluid Mech. 202, 295–317.CrossRefGoogle Scholar
Cambon, C., Mansour, N. N. & Godeferd, F. S. 1997 Energy transfer in rotating turbulence. J. Fluid Mech. 337, 303–332.CrossRefGoogle Scholar
Campanelli, L. 2016 On the self-similarity of nonhelical magnetohydrodynamic turbulence. Eur. Phys. J. C 6 (9), 504.CrossRefGoogle Scholar
Carati, D., Debliquy, O., Knaepen, B., Teaca, B. & Verma, M. 2006 Energy transfers in forced mhd turbulence. J. Turbul. 7 (51), 1–12.Google Scholar
Chandran, B. D. G. 2008 Strong anisotropic mhd turbulence with cross helicity. Astrophys. J. 685 (1), 646.CrossRefGoogle Scholar
Chandrasekhar, S. 1951 The invariant theory of isotropic turbulence in magneto-hydrodynamics. Proc. R. Soc. Lond. A 204 (1079), 435–449.Google Scholar
Diamond, P. H. & Biskamp, D. 1990 Comments on ‘dynamics of decaying two-dimensional magnetohydrodynamic turbulence’ [Phys. Fluids B 1, 1964 (1989)]. Phys. Fluids B 2 (3), 681–682.CrossRefGoogle Scholar
Dobrowolny, M., Mangeney, A. & Veltri, P. 1980 Fully developed anisotropic hydromagnetic turbulence in interplanetary space. Phys. Rev. Lett. 45 (2), 144–147.CrossRefGoogle Scholar
Favier, B., Godeferd, F. S., Cambon, C., Delache, A. & Bos, W. J. T. 2011 Quasi-static magnetohydrodynamic turbulence at high Reynolds number. J. Fluid Mech. 681, 434–461.CrossRefGoogle Scholar
Frisch, U., Pouquet, A., Léorat, J. & Mazure, A. 1975 Possibility of an inverse cascade of magnetic helicity in magnetohydrodynamic turbulence. J. Fluid Mech. 68, 769–778.CrossRefGoogle Scholar
Galtier, S. 2009 Wave turbulence in magnetized plasmas. Nonlinear Process. Geophys. 16 (1), 83–98.CrossRefGoogle Scholar
Galtier, S. 2016 Introduction to Modern Magnetohydrodynamics. Cambridge University Press.CrossRefGoogle Scholar
Galtier, S., Politano, H. & Pouquet, A. 1997 Self-similar energy decay in magnetohydrodynamic turbulence. Phys. Rev. Lett. 79 (15), 2807–2810.CrossRefGoogle Scholar
Galtier, S., Pouquet, A. & Mangeney, A. 2005 On spectral scaling laws for incompressible anisotropic magnetohydrodynamic turbulence. Phys. Plasmas 12 (9), 092310.CrossRefGoogle Scholar
Galtier, S., Zienicke, E., Politano, H. & Pouquet, A. 1999 Parametric investigation of self-similar decay laws in MHD turbulent flows. J. Plasma Phys. 61 (3), 507–541.CrossRefGoogle Scholar
George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids A 7, 1492–1509.CrossRefGoogle Scholar
Goldreich, P. & Sridhar, S. 1995 Toward a theory of interstellar turbulence. 2: strong Alfvenic turbulence. Astrophys. J. 438, 763–775.CrossRefGoogle Scholar
Gomez, T., Politano, H. & Pouquet, A. 1999 On the validity of a nonlocal approach for mhd turbulence. Phys. Fluids 11 (8), 2298–2306.CrossRefGoogle Scholar
Grappin, R., Frisch, U., Léorat, J. & Pouquet, A. 1982 Alfvenic fluctuations as asymptotic states of mhd turbulence. Astron. Astrophys. 105, 6–14.Google Scholar
Grappin, R., Pouquet, A. & Léorat, J. 1983 Dependence of mhd turbulence spectra on the velocity field-magnetic field correlation. Astron. Astrophys. 126, 51–58.Google Scholar
Grappin, R., Müller, W.-C. & Verdini, A. 2016 Alfvén-dynamo balance and magnetic excess in magnetohydrodynamic turbulence. Astron. & Astrophys. 589, A131.CrossRefGoogle Scholar
Haugen, N., Brandenburg, A. & Dobler, W. 2004 High-resolution simulations of nonhelical mhd turbulence. Astrophys. Space Sci. 292 (1), 53–60.CrossRefGoogle Scholar
Hossain, M., Gray, P. C., Pontius, D. H. Jr., Matthaeus, W. H. & Oughton, S. 1995 Phenomenology for the decay of energy-containing eddies in homogeneous mhd turbulence. Phys. Fluids 7 (11), 2886–2904.CrossRefGoogle Scholar
Iroshnikov, P. S. 1964 Turbulence of a conducting fluid in a strong magnetic field. Sov. Astron. 7 (4), 566–571.Google Scholar
Kalelkar, C. & Pandit, R. 2004 Decay of magnetohydrodynamic turbulence from power-law initial conditions. Phys. Rev. E 69, 046304.Google ScholarPubMed
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Kraichnan, R. H. 1965 Inertial-range spectrum of hydromagnetic turbulence. Phys. Fluids 8 (7), 1385–1387.CrossRefGoogle Scholar
Kraichnan, R. H. & Nagarajan, S. 1967 Growth of turbulent magnetic fields. Phys. Fluids 10 (4), 859–870.CrossRefGoogle Scholar
Lee, E., Brachet, M. E., Pouquet, A., Mininni, P. D. & Rosenberg, D. 2010 Lack of universality in decaying magnetohydrodynamic turbulence. Phys. Rev. E 81 (1), 016318.Google ScholarPubMed
Léorat, J., Pouquet, A. & Frisch, U. 1981 Fully developed mhd turbulence near critical magnetic Reynolds number. J. Fluid Mech. 104, 419–443.CrossRefGoogle Scholar
Lesieur, M. 2008 Turbulence in Fluids, 4th edn. Springer.CrossRefGoogle Scholar
Lesieur, M. & Ossia, S. 2000 3D isotropic turbulence at very high Reynolds numbers: EDQNM study. J. Turbul. 1, N7.CrossRefGoogle Scholar
Lesieur, M., Ossia, S. & Metais, O. 1999 Infrared pressure spectra in two- and three-dimensional isotropic incompressible turbulence. Phys. Fluids 11 (6), 1535–1543.CrossRefGoogle Scholar
Mason, J., Cattaneo, F. & Boldyrev, S. 2008 Numerical measurements of the spectrum in magnetohydrodynamic turbulence. Phys. Rev. E 77, 036403.Google ScholarPubMed
Matthaeus, W. H., Pouquet, A., Mininni, P. D., Dmitruk, P. & Breech, B. 2008 Rapid alignment of velocity and magnetic field in magnetohydrodynamic turbulence. Phys. Rev. Lett. 100, 085003.CrossRefGoogle ScholarPubMed
Meldi, M. & Sagaut, P. 2013a Further insights into self-similarity and self-preservation in freely decaying isotropic turbulence. J. Turbul. 14, 24–53.CrossRefGoogle Scholar
Meldi, M. & Sagaut, P. 2013b Pressure statistics in self-similar freely decaying isotropic turbulence. J. Fluid Mech. 717, R2, 1–12.Google Scholar
Mininni, P. D. & Pouquet, A. 2007 Energy spectra stemming from interactions of alfven waves and turbulent eddies. Phys. Rev. Lett. 99, 254502.CrossRefGoogle ScholarPubMed
Müller, W.-C. & Biskamp, D. 2000 Scaling properties of three-dimensional magnetohydrodynamic turbulence. Phys. Rev. Lett. 84 (3), 475–478.CrossRefGoogle ScholarPubMed
Müller, W.-C., Biskamp, D. & Grappin, R. 2003 Statistical anisotropy of magnetohydrodynamic turbulence. Phys. Rev. E 67, 066302.Google ScholarPubMed
Müller, W.-C. & Grappin, R. 2004 The residual energy in freely decaying magnetohydrodynamic turbulence. Plasma Phys. Control. Fusion 46, B91–B96.CrossRefGoogle Scholar
Müller, W.-C. & Grappin, R. 2005 Spectral energy dynamics in magnetohydrodynamic turbulence. Phys. Rev. Lett. 95, 114502.CrossRefGoogle ScholarPubMed
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41, 363–386.CrossRefGoogle Scholar
Perez, J. C. & Boldyrev, S. 2009 Role of cross-helicity in magnetohydrodynamic turbulence. Phys. Rev. Lett. 102, 025003.CrossRefGoogle ScholarPubMed
Perez, J. C., Mason, J., Boldyrev, S. & Cattaneo, F. 2012 On the energy spectrum of strong magnetohydrodynamic turbulence. Phys. Rev. X 2, 041005.Google Scholar
Politano, H., Gomez, T. & Pouquet, A. 2003 von Kármán-Howarth relationship for helical magnetohydrodynamic flows. Phys. Rev. E 68, 026315.Google ScholarPubMed
Politano, H. & Pouquet, A. 1998a Dynamical length scales for turbulent magnetized flows. Geophys. Res. Lett. 25 (3), 273–276.CrossRefGoogle Scholar
Politano, H. & Pouquet, A. 1998b von Kàrmàn-Howarth equation for magnetohydrodynamics and its consequences on third-order longitudinal structure and correlation functions. Phys. Rev. E 57 (1), R21–R24.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Pouquet, A. 1996 Turbulence, statistics and structures: an introduction. In Vth European School in Astrophysics, Lecture Notes in Physics ‘Plasma Astrophysics’, vol. 468, pp. 163–212. Springer.Google Scholar
Pouquet, A., Frisch, U. & Léorat, J.-L. 1976 Strong mhd helical turbulence and the nonlinear dynamo effect. J. Fluid Mech. 77, 321–354.CrossRefGoogle Scholar
Ristorcelli, J. R. 2006 Passive scalar mixing: analytic study of time scale ratio, variance, and mix rate. Phys. Fluids 18, 075101.CrossRefGoogle Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Wan, M., Oughton, S., Servidio, S. & Matthaeus, W. H. 2012 von Kármán self-preservation hypothesis for magnetohydrodynamic turbulence and its consequences for universality. J. Fluid Mech. 697, 296–315.CrossRefGoogle Scholar
Yoshimatsu, K. 2012 Examination of the four-fifths law for longitudinal third-order moments in incompressible magnetohydrodynamic turbulence in a periodic box. Phys. Rev. E 85, 066313.CrossRefGoogle Scholar
Yousef, T. A., Rincon, F. & Schekochihin, A. A. 2007 Exact scaling laws and the local structure of isotropic magnetohydrodynamic turbulence. J. Fluid Mech. 575, 111–120.CrossRefGoogle Scholar
Zhou, Y., Schilling, O. & Ghosh, S. 2002 Subgrid scale and backscatter model for magnetohydrodynamic turbulence based on closure theory: theoretical formulation. Phys. Rev. E 66, 026309.CrossRefGoogle ScholarPubMed