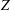1 Introduction
Impurities are always present in fusion plasmas, either due to unavoidable plasma–wall interaction, or through deliberate impurity injection. In the edge of a tokamak or stellarator, impurities can be beneficial, as they radiate energy and thus can mitigate the heat load on plasma-facing components. However, their ability to radiate energy is detrimental in the core of the plasma. It is thus crucial to understand how impurities are transported so that they do not accumulate in the core of the device.
There is a large body of theoretical research on the neoclassical transport of impurities in stellarators (Helander et al. Reference Helander, Newton, Mollén and Smith2017; Velasco et al. Reference Velasco, Calvo, Satake, Alonso, Nunami, Yokoyama, Sato, Estrada, Fontdecaba and Liniers2017; Calvo et al. Reference Calvo, Parra, Velasco, Alonso and na2018), which we shall not describe in detail. Far less has been done to study turbulent particle transport – either of impurities or of the bulk ions and electrons – and most of these studies rely on quasi-linear transport theory (Mikkelsen et al. Reference Mikkelsen, Tanaka, Nunami, Watanabe, Sugama, Yoshinuma, Ida, Suzuki, Goto and Morita2014). Recently, however, there have been direct numerical simulations of turbulence in impure stellarator plasmas using gyrokinetic codes (Nunami et al. Reference Nunami, Nakata, Toda and Sugama2020).
Recent measurement in the stellarator Wendelstein 7-X indicate that the impurity transport is dominated by turbulent diffusion (Langenberg et al. Reference Langenberg, Warmer, Fuchert, Marchuk, Dinklage, Wegner, Alonso, Bozhenkov, Brunner and Burhenn2018; Geiger et al. Reference Geiger, Wegner, Beidler, Burhenn, Buttenschön, Dux, Langenberg, Pablant, Pütterich and Turkin2019). Diffusion coefficients two orders of magnitude larger than those calculated from collisional transport have been measured for iron impurities (Geiger et al. Reference Geiger, Wegner, Beidler, Burhenn, Buttenschön, Dux, Langenberg, Pablant, Pütterich and Turkin2019), and the impurity confinement time appears to be insensitive to the impurity charge number (Langenberg et al. Reference Langenberg, Wegner, Pablant, Marchuk, Geiger, Tamura, Bussiahn, Kubkowska, Mollén and Traverso2020) – in contradiction to predictions for collisional transport (Helander & Sigmar Reference Helander and Sigmar2005).
On the other hand, the experimental observations may be consistent with recent theoretical calculations of the transport due to electrostatic turbulence (Helander & Zocco Reference Helander and Zocco2018), which, for heavy species, give transport coefficients independent of the impurity charge and mass (Angioni et al. Reference Angioni, Bilato, Casson, Fable, Mantica, Odstrcil and Valisa2016; Helander & Zocco Reference Helander and Zocco2018). However, the calculation by Helander & Zocco (Reference Helander and Zocco2018) does not include collisions, which could have a significant effect on heavy impurities due to their high charge and high collision frequency. The present paper addresses this shortcoming by including collisions in the calculation of the quasi-linear impurity flux.
Previous analytical work has shown that collisions with the impurities themselves do not significantly affect the impurity flux in tokamaks (Pusztai et al. Reference Pusztai, Mollén, Fülöp and Candy2013). This calculation can be generalized, without additional complications, to also apply to stellarators, which is done in § 3.1. However, Pusztai et al. (Reference Pusztai, Mollén, Fülöp and Candy2013) considered non-trace impurities, which allowed them to neglect the collisions between impurities and bulk ions, which could, in principle, modify the impurity flux. In § 3.2, we show that impurity–ion collisions provide only a small correction to the previous results unless the charge number of the impurities is comparable to the inverse bulk-ion collisionality. Our result thus strengthens the conclusions of Helander & Zocco (Reference Helander and Zocco2018) and Pusztai et al. (Reference Pusztai, Mollén, Fülöp and Candy2013) for low collisionality plasmas, and generalizes parts of the calculation of Pusztai et al. (Reference Pusztai, Mollén, Fülöp and Candy2013) to stellarator geometry.
2 Equation for heavy impurities
The linearized electrostatic gyrokinetic equation for impurities is
where ![]() $g_{z}$ is the non-adiabatic part of the perturbed impurity distribution function,
$g_{z}$ is the non-adiabatic part of the perturbed impurity distribution function, ![]() $g_{z}=f_{z}-(1-Ze\unicode[STIX]{x1D719}/T_{z})f_{Mz}$,
$g_{z}=f_{z}-(1-Ze\unicode[STIX]{x1D719}/T_{z})f_{Mz}$, ![]() $f_{z}$ the full impurity distribution function,
$f_{z}$ the full impurity distribution function, ![]() $f_{Mz}$ a Maxwellian with temperature
$f_{Mz}$ a Maxwellian with temperature ![]() $T_{z}$ and density
$T_{z}$ and density ![]() $n_{z}$,
$n_{z}$,
with ![]() $m_{z}$ the mass of the impurity,
$m_{z}$ the mass of the impurity, ![]() $\unicode[STIX]{x1D719}$ the fluctuating electrostatic potential and
$\unicode[STIX]{x1D719}$ the fluctuating electrostatic potential and ![]() $e$ the elementary charge. Both
$e$ the elementary charge. Both ![]() $g_{z}$ and
$g_{z}$ and ![]() $\unicode[STIX]{x1D719}$ have been written as
$\unicode[STIX]{x1D719}$ have been written as ![]() $g_{z}={\hat{g}}_{z}(l)\text{e}^{-\text{i}\unicode[STIX]{x1D714}t+\text{i}S}$, where (in ballooning space)
$g_{z}={\hat{g}}_{z}(l)\text{e}^{-\text{i}\unicode[STIX]{x1D714}t+\text{i}S}$, where (in ballooning space) ![]() $S$ satisfies
$S$ satisfies ![]() $\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}S=0$ and
$\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}S=0$ and ![]() $\unicode[STIX]{x1D735}S=\boldsymbol{k}_{\bot }$, where
$\unicode[STIX]{x1D735}S=\boldsymbol{k}_{\bot }$, where ![]() $\boldsymbol{B}$ is the magnetic field and
$\boldsymbol{B}$ is the magnetic field and ![]() $l$ is the arc length along
$l$ is the arc length along ![]() $\boldsymbol{B}$. The magnetic field is written as
$\boldsymbol{B}$. The magnetic field is written as ![]() $\boldsymbol{B}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}$, and the wave vector as
$\boldsymbol{B}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}$, and the wave vector as ![]() $\boldsymbol{k}_{\bot }=k_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}+k_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}$. The drift frequency is
$\boldsymbol{k}_{\bot }=k_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}+k_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}$. The drift frequency is ![]() $\unicode[STIX]{x1D714}_{d}=\boldsymbol{k}_{\bot }\boldsymbol{\cdot }\boldsymbol{v}_{d}$, where
$\unicode[STIX]{x1D714}_{d}=\boldsymbol{k}_{\bot }\boldsymbol{\cdot }\boldsymbol{v}_{d}$, where ![]() $\boldsymbol{v}_{d}$ is the drift velocity
$\boldsymbol{v}_{d}$ is the drift velocity
where ![]() $\boldsymbol{b}=\boldsymbol{B}/B$,
$\boldsymbol{b}=\boldsymbol{B}/B$, ![]() $B=|\boldsymbol{B}|$,
$B=|\boldsymbol{B}|$, ![]() $\unicode[STIX]{x1D6FA}_{z}=ZeB/m_{z}$;
$\unicode[STIX]{x1D6FA}_{z}=ZeB/m_{z}$; ![]() $v_{\Vert }$ and
$v_{\Vert }$ and ![]() $v_{\bot }$ are the speeds in the directions parallel and perpendicular to
$v_{\bot }$ are the speeds in the directions parallel and perpendicular to ![]() $\boldsymbol{B}$. The collision operator
$\boldsymbol{B}$. The collision operator ![]() $C$ will be specified explicitly in § 3. The diamagnetic frequency is
$C$ will be specified explicitly in § 3. The diamagnetic frequency is ![]() $\unicode[STIX]{x1D714}_{\ast z}^{\text{T}}=\unicode[STIX]{x1D714}_{\ast z}(1+\unicode[STIX]{x1D702}_{z}[x^{3}-3/2])$, where
$\unicode[STIX]{x1D714}_{\ast z}^{\text{T}}=\unicode[STIX]{x1D714}_{\ast z}(1+\unicode[STIX]{x1D702}_{z}[x^{3}-3/2])$, where ![]() $\unicode[STIX]{x1D714}_{\ast z}=(k_{\unicode[STIX]{x1D6FC}}T_{z}/Ze)\,\text{d}\,\ln \,n_{z}/\text{d}\unicode[STIX]{x1D713}$,
$\unicode[STIX]{x1D714}_{\ast z}=(k_{\unicode[STIX]{x1D6FC}}T_{z}/Ze)\,\text{d}\,\ln \,n_{z}/\text{d}\unicode[STIX]{x1D713}$, ![]() $\unicode[STIX]{x1D702}_{z}=\text{d}\,\ln \,T_{z}/\text{d}\,\ln \,n_{z}$ and
$\unicode[STIX]{x1D702}_{z}=\text{d}\,\ln \,T_{z}/\text{d}\,\ln \,n_{z}$ and ![]() $x=v/v_{Tz}$ with
$x=v/v_{Tz}$ with ![]() $v_{Tz}=\sqrt{2T_{z}/m_{z}}$.
$v_{Tz}=\sqrt{2T_{z}/m_{z}}$. ![]() $\text{J}_{0}=\text{J}_{0}(k_{\bot }v_{\bot }/\unicode[STIX]{x1D6FA}_{z})$, where
$\text{J}_{0}=\text{J}_{0}(k_{\bot }v_{\bot }/\unicode[STIX]{x1D6FA}_{z})$, where ![]() $\text{J}_{0}$ is the zeroth-order Bessel function of the first kind. In (2.1) and throughout the rest of this paper, gradients are taken with
$\text{J}_{0}$ is the zeroth-order Bessel function of the first kind. In (2.1) and throughout the rest of this paper, gradients are taken with ![]() $\unicode[STIX]{x1D706}=v_{\bot }^{2}/(Bv^{2})$ and
$\unicode[STIX]{x1D706}=v_{\bot }^{2}/(Bv^{2})$ and ![]() $v$ fixed. The derivation of (2.1) assumes that the electrostatic potential perturbations have low amplitude, in the sense that
$v$ fixed. The derivation of (2.1) assumes that the electrostatic potential perturbations have low amplitude, in the sense that ![]() $Ze\hat{\unicode[STIX]{x1D719}}/T_{z}\ll 1$, and that the deviation of the background potential from a flux function is similarly small. If these conditions are violated, the potential variations would cause
$Ze\hat{\unicode[STIX]{x1D719}}/T_{z}\ll 1$, and that the deviation of the background potential from a flux function is similarly small. If these conditions are violated, the potential variations would cause ![]() $n_{z}$ to vary on the flux surface, and (2.1) would not be valid. Such large variations in the background potential have been observed experimentally and studied theoretically for both tokamaks (Fülöp & Moradi Reference Fülöp and Moradi2011; Reinke et al. Reference Reinke, Hutchinson, Rice, Howard, Bader, Wukitch, Lin, Pace, Hubbard and Hughes2012) and stellarators (Pedrosa et al. Reference Pedrosa, Alonso, García-Regaña, Hidalgo, Velasco, Calvo, Kleiber, Silva and Helander2015; García-Regaña et al. Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maaßberg, Smith and Turkin2017), but will not be considered here.
$n_{z}$ to vary on the flux surface, and (2.1) would not be valid. Such large variations in the background potential have been observed experimentally and studied theoretically for both tokamaks (Fülöp & Moradi Reference Fülöp and Moradi2011; Reinke et al. Reference Reinke, Hutchinson, Rice, Howard, Bader, Wukitch, Lin, Pace, Hubbard and Hughes2012) and stellarators (Pedrosa et al. Reference Pedrosa, Alonso, García-Regaña, Hidalgo, Velasco, Calvo, Kleiber, Silva and Helander2015; García-Regaña et al. Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maaßberg, Smith and Turkin2017), but will not be considered here.
Given a solution to (2.1), we calculate the quasi-linear impurity flux using (Helander & Zocco Reference Helander and Zocco2018)
where ![]() ${\mathcal{I}}$ denotes the imaginary part and the brackets denote a flux-surface average
${\mathcal{I}}$ denotes the imaginary part and the brackets denote a flux-surface average
2.1 Expansion in powers of  $Z^{-1}$
$Z^{-1}$
Like Pusztai et al. (Reference Pusztai, Mollén, Fülöp and Candy2013), we solve (2.1) for a highly charged impurity species by expanding the equation in powers of ![]() $Z$. We assume
$Z$. We assume
corresponding to a highly charged, heavy trace impurity species. As the impurities are only a trace, they will not affect the electrostatic potential, which is set by the bulk ions and electrons. Thus, we assume that the impurities merely respond to ion-scale turbulence, and that ![]() $\unicode[STIX]{x1D714}$ is comparable to the ion diamagnetic frequency
$\unicode[STIX]{x1D714}$ is comparable to the ion diamagnetic frequency ![]() $\unicode[STIX]{x1D714}_{\ast i}$. We order the impurity frequencies in powers of
$\unicode[STIX]{x1D714}_{\ast i}$. We order the impurity frequencies in powers of ![]() $Z$ by relating them to the corresponding bulk-ion frequencies
$Z$ by relating them to the corresponding bulk-ion frequencies
where we order the bulk-ion frequencies as similar ![]() $\unicode[STIX]{x1D714}_{bi}\sim \unicode[STIX]{x1D714}_{di}$. Here,
$\unicode[STIX]{x1D714}_{bi}\sim \unicode[STIX]{x1D714}_{di}$. Here, ![]() $\unicode[STIX]{x1D714}_{ba}$ is the bounce or transit frequency of species
$\unicode[STIX]{x1D714}_{ba}$ is the bounce or transit frequency of species ![]() $a$,
$a$, ![]() $v_{\Vert }\unicode[STIX]{x1D735}_{\Vert }g_{a}\sim \unicode[STIX]{x1D714}_{ba}g_{a}$. The collision operator is ordered as
$v_{\Vert }\unicode[STIX]{x1D735}_{\Vert }g_{a}\sim \unicode[STIX]{x1D714}_{ba}g_{a}$. The collision operator is ordered as
As the turbulence is set by the bulk species, ![]() $k_{\bot }$ is independent of
$k_{\bot }$ is independent of ![]() $Z$ and
$Z$ and ![]() $k_{\bot }v_{\bot }\unicode[STIX]{x1D6FA}_{z}$ thus scales as
$k_{\bot }v_{\bot }\unicode[STIX]{x1D6FA}_{z}$ thus scales as ![]() $Z^{-1}$.
$Z^{-1}$.
We expand ![]() ${\hat{g}}_{z}$ and (2.1) in powers of
${\hat{g}}_{z}$ and (2.1) in powers of ![]() $Z^{-1}$,
$Z^{-1}$,
where ![]() ${\hat{g}}_{z}^{(n)}/{\hat{g}}_{z}^{(0)}\sim Z^{-n}$.
${\hat{g}}_{z}^{(n)}/{\hat{g}}_{z}^{(0)}\sim Z^{-n}$.
The ![]() $Z^{0}$-order equation becomes
$Z^{0}$-order equation becomes
which has the solution ![]() ${\hat{g}}_{z}^{(0)}=(Ze\hat{\unicode[STIX]{x1D719}}/T_{z})\,f_{Mz}$, and gives no impurity flux when inserted into (2.4).
${\hat{g}}_{z}^{(0)}=(Ze\hat{\unicode[STIX]{x1D719}}/T_{z})\,f_{Mz}$, and gives no impurity flux when inserted into (2.4).
The ![]() $Z^{-1/2}$-order equation is
$Z^{-1/2}$-order equation is
so that also ![]() ${\hat{g}}_{z}^{(1/2)}$ yields no flux when inserted into (2.4), since
${\hat{g}}_{z}^{(1/2)}$ yields no flux when inserted into (2.4), since
for collisions that preserve the number of impurities.
The ![]() $Z^{-1}$-order equation is
$Z^{-1}$-order equation is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D714}{\hat{g}}_{z}^{(1)}-\text{i}C[{\hat{g}}_{z}^{(1)}]\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D714}_{\text{d}z}{\hat{g}}_{z}^{(0)}-\text{i}v_{\Vert }\unicode[STIX]{x1D735}_{\Vert }{\hat{g}}_{z}^{(1/2)}-\unicode[STIX]{x1D714}_{\ast z}^{\text{T}}\frac{Ze\hat{\unicode[STIX]{x1D719}}}{T_{z}}f_{Mz}-\unicode[STIX]{x1D714}\frac{k_{\bot }^{2}v_{\bot }^{2}}{4\unicode[STIX]{x1D6FA}_{z}^{2}}\frac{Ze\hat{\unicode[STIX]{x1D719}}}{T_{z}}f_{Mz},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D714}{\hat{g}}_{z}^{(1)}-\text{i}C[{\hat{g}}_{z}^{(1)}]\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D714}_{\text{d}z}{\hat{g}}_{z}^{(0)}-\text{i}v_{\Vert }\unicode[STIX]{x1D735}_{\Vert }{\hat{g}}_{z}^{(1/2)}-\unicode[STIX]{x1D714}_{\ast z}^{\text{T}}\frac{Ze\hat{\unicode[STIX]{x1D719}}}{T_{z}}f_{Mz}-\unicode[STIX]{x1D714}\frac{k_{\bot }^{2}v_{\bot }^{2}}{4\unicode[STIX]{x1D6FA}_{z}^{2}}\frac{Ze\hat{\unicode[STIX]{x1D719}}}{T_{z}}f_{Mz},\end{eqnarray}$$ where we have expanded the Bessel function ![]() $\text{J}_{0}$. The corresponding particle flux receives contributions from all but the last term on the right-hand side
$\text{J}_{0}$. The corresponding particle flux receives contributions from all but the last term on the right-hand side
The terms in this expression are fluxes due to magnetic curvature, parallel compressibility (Angioni & Peeters Reference Angioni and Peeters2006) and ordinary diffusion. The curvature and diffusion terms were also found by Helander & Zocco (Reference Helander and Zocco2018), along with a thermodiffusion term, which is smaller in ![]() $Z^{-1}$ and thus absent to this order. The parallel compressibility term is absent in the calculation of Helander & Zocco (Reference Helander and Zocco2018), since no distinction was made between the smallness of the impurity bounce and drift frequencies, but our results otherwise agree with those of Helander & Zocco (Reference Helander and Zocco2018).
$Z^{-1}$ and thus absent to this order. The parallel compressibility term is absent in the calculation of Helander & Zocco (Reference Helander and Zocco2018), since no distinction was made between the smallness of the impurity bounce and drift frequencies, but our results otherwise agree with those of Helander & Zocco (Reference Helander and Zocco2018).
In (2.17), collisions give no direct contribution to the flux, but will affect the flux indirectly through ![]() $g_{z}^{(1/2)}$ in the parallel compressibility term. To quantify the effects of collisions, we thus have to solve (2.14) for
$g_{z}^{(1/2)}$ in the parallel compressibility term. To quantify the effects of collisions, we thus have to solve (2.14) for ![]() $g_{z}^{(1/2)}$, which we do in the next section. Once an expression for
$g_{z}^{(1/2)}$, which we do in the next section. Once an expression for ![]() $g_{z}^{(1/2)}$ has been obtained, we can then estimate the importance of collisions by comparing the flux due to the parallel compressibility with the ordinary diffusive flux.
$g_{z}^{(1/2)}$ has been obtained, we can then estimate the importance of collisions by comparing the flux due to the parallel compressibility with the ordinary diffusive flux.
3 Solving for  ${\hat{g}}_{z}^{(1/2)}$
${\hat{g}}_{z}^{(1/2)}$
Before solving (2.14), we note that only the part of ![]() ${\hat{g}}_{z}^{(1/2)}$ that is odd in
${\hat{g}}_{z}^{(1/2)}$ that is odd in ![]() $v_{\Vert }$ will contribute to the flux (2.17). We thus split (2.14) into an odd and even part, where the odd part is
$v_{\Vert }$ will contribute to the flux (2.17). We thus split (2.14) into an odd and even part, where the odd part is
where the ‘![]() $-$’ superscript indicates the part of
$-$’ superscript indicates the part of ![]() ${\hat{g}}_{z}$ and
${\hat{g}}_{z}$ and ![]() $C[{\hat{g}}_{z}^{(1/2)}]$ that is odd in
$C[{\hat{g}}_{z}^{(1/2)}]$ that is odd in ![]() $v_{\Vert }$.
$v_{\Vert }$.
To solve (3.1), we need an explicit expression for the collision operator. We write
where ![]() $C_{zz}$ and
$C_{zz}$ and ![]() $C_{zi}$ are the impurity–impurity and impurity–ion collision operators, respectively. In the limit where finite Larmor-radius effects can be neglected, we can use the expressions for the Fokker–Planck collision operator from collisional transport theory directly on
$C_{zi}$ are the impurity–impurity and impurity–ion collision operators, respectively. In the limit where finite Larmor-radius effects can be neglected, we can use the expressions for the Fokker–Planck collision operator from collisional transport theory directly on ![]() ${\hat{g}}_{z}$. This is easily justifiable for the impurities, which have a small Larmor radius due to their large charge. For the reminder of this paper, we thus simplify the notation by omitting the hats on
${\hat{g}}_{z}$. This is easily justifiable for the impurities, which have a small Larmor radius due to their large charge. For the reminder of this paper, we thus simplify the notation by omitting the hats on ![]() $g_{z}$ and
$g_{z}$ and ![]() $\unicode[STIX]{x1D719}$.
$\unicode[STIX]{x1D719}$.
The relative size of the impurity–impurity and impurity–ion operators is (Helander & Sigmar Reference Helander and Sigmar2005)
and will be taken to be ![]() $O(1)$ in our orderings. For purely illustrative purposes, it is nevertheless instructive to consider the limit where
$O(1)$ in our orderings. For purely illustrative purposes, it is nevertheless instructive to consider the limit where ![]() $C_{zz}[g_{z}]\gg C_{zi}[g_{z}]$, to demonstrate why impurity–impurity collisions cannot affect the impurity flux.
$C_{zz}[g_{z}]\gg C_{zi}[g_{z}]$, to demonstrate why impurity–impurity collisions cannot affect the impurity flux.
3.1 Impurity–impurity collisions only
For ![]() $C[g_{z}^{(1/2)}]\approx C_{zz}[g_{z}^{(1/2)}]$,
$C[g_{z}^{(1/2)}]\approx C_{zz}[g_{z}^{(1/2)}]$, ![]() $g_{z}^{(1/2)}\propto v_{\Vert }\,f_{M}$ is in the null space of the collision operator (Helander & Sigmar Reference Helander and Sigmar2005), in the sense that
$g_{z}^{(1/2)}\propto v_{\Vert }\,f_{M}$ is in the null space of the collision operator (Helander & Sigmar Reference Helander and Sigmar2005), in the sense that ![]() $C_{zz}[v_{\Vert }\,f_{M}]=0$. The solution to (3.1) then becomes
$C_{zz}[v_{\Vert }\,f_{M}]=0$. The solution to (3.1) then becomes
This result, previously found by Pusztai et al. (Reference Pusztai, Mollén, Fülöp and Candy2013), would also have been obtained from (3.1) without the collision operator, and is thus not affected by impurity–impurity collisions.
Inserting (3.4) into (2.17) and writing ![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{r}+\text{i}\unicode[STIX]{x1D6FE}$, the parallel compressibility contribution to the particle flux becomes
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{r}+\text{i}\unicode[STIX]{x1D6FE}$, the parallel compressibility contribution to the particle flux becomes
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{z}^{\text{comp}} & = & \displaystyle k_{\unicode[STIX]{x1D6FC}}{\mathcal{I}}\frac{Ze}{T_{z}}\left\langle \int f_{Mz}\frac{v_{\Vert }}{\unicode[STIX]{x1D714}^{2}}\unicode[STIX]{x1D735}_{\Vert }\left(v_{\Vert }\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D719}\right)\unicode[STIX]{x1D719}^{\ast }\text{d}^{3}v\right\rangle \nonumber\\ \displaystyle & = & \displaystyle -k_{\unicode[STIX]{x1D6FC}}\frac{Ze}{m_{z}}n_{z}\left\langle |\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D719}|^{2}\right\rangle {\mathcal{I}}\frac{1}{\unicode[STIX]{x1D714}^{2}}.\nonumber\\ \displaystyle & = & \displaystyle \frac{2\unicode[STIX]{x1D714}_{r}\unicode[STIX]{x1D6FE}k_{\unicode[STIX]{x1D6FC}}}{(\unicode[STIX]{x1D714}_{r}^{2}+\unicode[STIX]{x1D6FE}^{2})^{2}}\frac{Ze}{m_{z}}n_{z}\left\langle |\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D719}|^{2}\right\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{z}^{\text{comp}} & = & \displaystyle k_{\unicode[STIX]{x1D6FC}}{\mathcal{I}}\frac{Ze}{T_{z}}\left\langle \int f_{Mz}\frac{v_{\Vert }}{\unicode[STIX]{x1D714}^{2}}\unicode[STIX]{x1D735}_{\Vert }\left(v_{\Vert }\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D719}\right)\unicode[STIX]{x1D719}^{\ast }\text{d}^{3}v\right\rangle \nonumber\\ \displaystyle & = & \displaystyle -k_{\unicode[STIX]{x1D6FC}}\frac{Ze}{m_{z}}n_{z}\left\langle |\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D719}|^{2}\right\rangle {\mathcal{I}}\frac{1}{\unicode[STIX]{x1D714}^{2}}.\nonumber\\ \displaystyle & = & \displaystyle \frac{2\unicode[STIX]{x1D714}_{r}\unicode[STIX]{x1D6FE}k_{\unicode[STIX]{x1D6FC}}}{(\unicode[STIX]{x1D714}_{r}^{2}+\unicode[STIX]{x1D6FE}^{2})^{2}}\frac{Ze}{m_{z}}n_{z}\left\langle |\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D719}|^{2}\right\rangle .\end{eqnarray}$$ The right-hand side of (3.5) follows from ![]() $\langle B\unicode[STIX]{x1D735}_{\Vert }X\rangle =0$ for any single valued
$\langle B\unicode[STIX]{x1D735}_{\Vert }X\rangle =0$ for any single valued ![]() $X$; also recall that
$X$; also recall that ![]() $\unicode[STIX]{x1D706}$ and
$\unicode[STIX]{x1D706}$ and ![]() $v$ are kept fixed when evaluating
$v$ are kept fixed when evaluating ![]() $\unicode[STIX]{x1D735}v_{\Vert }$. We compare this flux to the flux due to ordinary diffusion. From the last term in (2.17), the diffusive flux is of the size
$\unicode[STIX]{x1D735}v_{\Vert }$. We compare this flux to the flux due to ordinary diffusion. From the last term in (2.17), the diffusive flux is of the size
whereupon the relative contribution of (3.5) to the flux becomes
where we have used ![]() $\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D719}\sim k_{\Vert }\unicode[STIX]{x1D719}$, recalled
$\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D719}\sim k_{\Vert }\unicode[STIX]{x1D719}$, recalled ![]() $\unicode[STIX]{x1D714}\sim \unicode[STIX]{x1D714}_{\ast i}\sim k_{\bot }\unicode[STIX]{x1D70C}_{i}v_{Ti}/a$, used
$\unicode[STIX]{x1D714}\sim \unicode[STIX]{x1D714}_{\ast i}\sim k_{\bot }\unicode[STIX]{x1D70C}_{i}v_{Ti}/a$, used ![]() $k_{\unicode[STIX]{x1D6FC}}\sim k_{\bot }a$ and
$k_{\unicode[STIX]{x1D6FC}}\sim k_{\bot }a$ and ![]() $\text{d}\ln n_{z}/\text{d}\unicode[STIX]{x1D713}\sim 1/(Ba^{2})$. Here,
$\text{d}\ln n_{z}/\text{d}\unicode[STIX]{x1D713}\sim 1/(Ba^{2})$. Here, ![]() $a$ is the minor radius. For a stellarator with
$a$ is the minor radius. For a stellarator with ![]() $N$ field periods and major radius
$N$ field periods and major radius ![]() $R$, we can use the rough estimate
$R$, we can use the rough estimate
based on the picture of ![]() $\unicode[STIX]{x1D719}$ as a standing wave on each period of the stellarator (Kornilov et al. Reference Kornilov, Kleiber, Hatzky, Villard and Jost2004; Helander et al. Reference Helander, Beidler, Bird, Drevlak, Feng, Hatzky, Jenko, Kleiber, Proll and Turkin2012). The ratio (3.7) thus scales as the inverse aspect ratio squared. For parameters typical of ion-temperature-gradient turbulence in Wendelstein 7-X (
$\unicode[STIX]{x1D719}$ as a standing wave on each period of the stellarator (Kornilov et al. Reference Kornilov, Kleiber, Hatzky, Villard and Jost2004; Helander et al. Reference Helander, Beidler, Bird, Drevlak, Feng, Hatzky, Jenko, Kleiber, Proll and Turkin2012). The ratio (3.7) thus scales as the inverse aspect ratio squared. For parameters typical of ion-temperature-gradient turbulence in Wendelstein 7-X (![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim 10^{-1}$ to
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim 10^{-1}$ to ![]() $10^{0}$;
$10^{0}$; ![]() $k_{\Vert }a\sim 2.5\times 10^{-1}$), the ratio (3.7) is approximately 5 to
$k_{\Vert }a\sim 2.5\times 10^{-1}$), the ratio (3.7) is approximately 5 to ![]() $5\times 10^{-2}$, where the larger value corresponds to turbulence with smaller
$5\times 10^{-2}$, where the larger value corresponds to turbulence with smaller ![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}$.
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$.
We thus conclude that parallel compressibility could contribute significantly to the impurity flux. In the next section, we show how this contribution is modified by impurity–ion collisions.
3.2 Effects of impurity–ion collisions
We have shown that impurity self-collisions have no effect on the quasi-linear particle flux of highly charged impurities. This result is applicable in the limit where highly charged impurities are a trace ![]() $Z^{2}n_{z}/n_{i}\ll 1$ with exceptionally large mass,
$Z^{2}n_{z}/n_{i}\ll 1$ with exceptionally large mass, ![]() $\sqrt{m_{z}/m_{i}}\gg n_{i}/(Z^{2}n_{z})$, and hinges on the fact that the solution to (3.1) without impurity–impurity collisions is in the null space of
$\sqrt{m_{z}/m_{i}}\gg n_{i}/(Z^{2}n_{z})$, and hinges on the fact that the solution to (3.1) without impurity–impurity collisions is in the null space of ![]() $C_{zz}$. To generalize these results to impurities without exceptionally large mass, we need to include the effects of impurity–ion collisions.
$C_{zz}$. To generalize these results to impurities without exceptionally large mass, we need to include the effects of impurity–ion collisions.
Neglecting finite Larmor-radius effects, the impurity–ion collision operator is (to lowest order in ![]() $\sqrt{m_{i}/m_{z}}$) (Calvo et al. Reference Calvo, Parra, Velasco and García-Regaña2019)
$\sqrt{m_{i}/m_{z}}$) (Calvo et al. Reference Calvo, Parra, Velasco and García-Regaña2019)
 $$\begin{eqnarray}\displaystyle & & \displaystyle C_{zi}^{-}[g_{z}^{(1/2)}]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{4}{3\sqrt{\unicode[STIX]{x03C0}}}\sqrt{\frac{m_{i}}{m_{z}}}\hat{\unicode[STIX]{x1D708}}_{zi}\left({\mathcal{K}}[g_{z}^{(1/2)-}]+\frac{m_{z}v_{\Vert }A}{T_{z}}f_{Mz}\right);\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle C_{zi}^{-}[g_{z}^{(1/2)}]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{4}{3\sqrt{\unicode[STIX]{x03C0}}}\sqrt{\frac{m_{i}}{m_{z}}}\hat{\unicode[STIX]{x1D708}}_{zi}\left({\mathcal{K}}[g_{z}^{(1/2)-}]+\frac{m_{z}v_{\Vert }A}{T_{z}}f_{Mz}\right);\end{eqnarray}$$where
with ![]() $\unicode[STIX]{x1D735}_{v}$ the gradient operator in velocity space; and
$\unicode[STIX]{x1D735}_{v}$ the gradient operator in velocity space; and
where ![]() $f_{i}$ is the bulk-ion distribution;
$f_{i}$ is the bulk-ion distribution; ![]() $A$ can be interpreted as the flow velocity the impurities would reach due to collisions with the bulk ions, in the absence of other forces (Calvo et al. Reference Calvo, Parra, Velasco and García-Regaña2019). The collision frequency is
$A$ can be interpreted as the flow velocity the impurities would reach due to collisions with the bulk ions, in the absence of other forces (Calvo et al. Reference Calvo, Parra, Velasco and García-Regaña2019). The collision frequency is
with ![]() $\ln \unicode[STIX]{x1D6EC}$ the Coulomb logarithm and
$\ln \unicode[STIX]{x1D6EC}$ the Coulomb logarithm and ![]() $\unicode[STIX]{x1D716}_{0}$ the permittivity of vacuum. To simplify the notation, we also introduce the modified impurity–ion collision frequency
$\unicode[STIX]{x1D716}_{0}$ the permittivity of vacuum. To simplify the notation, we also introduce the modified impurity–ion collision frequency
The operator (3.9) is a mass-ratio expanded Fokker–Planck operator; the general Fokker–Planck operator implemented in several gyrokinetic codes (Candy, Belli & Bravenec Reference Candy, Belli and Bravenec2016; Pan & Ernst Reference Pan and Ernst2019) should thus reduce to the above operator in the appropriate limit.
With ![]() $C=C_{zz}+C_{zi}$ in (3.1), the ansatz
$C=C_{zz}+C_{zi}$ in (3.1), the ansatz ![]() $g_{z}^{(1/2)-}\propto v_{\Vert }\,f_{Mz}(v)$ yields
$g_{z}^{(1/2)-}\propto v_{\Vert }\,f_{Mz}(v)$ yields
where we have used ![]() $C_{zz}[v_{\Vert }\,f_{Mz}]=0$ and
$C_{zz}[v_{\Vert }\,f_{Mz}]=0$ and ![]() ${\mathcal{K}}[v_{\Vert }f_{Mz}]=-v_{\Vert }\,f_{Mz}$. Note that impurity–impurity collisions again have no effect, as the solution is in the null space of
${\mathcal{K}}[v_{\Vert }f_{Mz}]=-v_{\Vert }\,f_{Mz}$. Note that impurity–impurity collisions again have no effect, as the solution is in the null space of ![]() $C_{zz}$. Impurity–ion collisions, on the other hand, both modify the response to the parallel electric field, and provide a new source for
$C_{zz}$. Impurity–ion collisions, on the other hand, both modify the response to the parallel electric field, and provide a new source for ![]() $g_{z}^{(1/2)-}$ through the friction force between the impurities and bulk ions.
$g_{z}^{(1/2)-}$ through the friction force between the impurities and bulk ions.
The relative size of the ion–impurity friction and the electric field terms in (3.14) is, assuming ![]() $e\unicode[STIX]{x1D719}/T_{z}\sim \unicode[STIX]{x1D70C}_{i}/a$,
$e\unicode[STIX]{x1D719}/T_{z}\sim \unicode[STIX]{x1D70C}_{i}/a$, ![]() $A\sim \unicode[STIX]{x1D70C}_{i}v_{Ti}/a$ (appropriate since
$A\sim \unicode[STIX]{x1D70C}_{i}v_{Ti}/a$ (appropriate since ![]() $A$ is a flow velocity),
$A$ is a flow velocity),
which is essentially ![]() $Z$ times the bulk-ion collisionality divided by
$Z$ times the bulk-ion collisionality divided by ![]() $k_{\Vert }a$. As any fusion reactor will be in a low collisionality regime
$k_{\Vert }a$. As any fusion reactor will be in a low collisionality regime ![]() $a\hat{\unicode[STIX]{x1D708}}_{ii}/v_{Ti}\ll 1$, the above ratio will likely be small. However, it can be significant in smaller fusion experiments, such as TJ-II, as shown in table 1. Likewise, the effect of the
$a\hat{\unicode[STIX]{x1D708}}_{ii}/v_{Ti}\ll 1$, the above ratio will likely be small. However, it can be significant in smaller fusion experiments, such as TJ-II, as shown in table 1. Likewise, the effect of the ![]() $\text{i}\unicode[STIX]{x1D708}_{zi}^{\prime }$ in the denominator can be estimated as
$\text{i}\unicode[STIX]{x1D708}_{zi}^{\prime }$ in the denominator can be estimated as
which again scales as ![]() $Z$ times the bulk-ion collisionality. Thus, in the limit where
$Z$ times the bulk-ion collisionality. Thus, in the limit where ![]() $\unicode[STIX]{x1D6E4}_{z}^{\text{comp}}$ is significant (the ratio (3.7) is large,
$\unicode[STIX]{x1D6E4}_{z}^{\text{comp}}$ is significant (the ratio (3.7) is large, ![]() $k_{\Vert }a>k_{\bot }\unicode[STIX]{x1D70C}_{i}$), the collisional modification of the response to
$k_{\Vert }a>k_{\bot }\unicode[STIX]{x1D70C}_{i}$), the collisional modification of the response to ![]() $\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D719}$ in (3.14) is more important than the drive due to ion–impurity friction, but both of these modifications are likely small in the Large Helical Device and Wendelstein 7-X, and will be yet smaller in a fusion reactor.
$\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D719}$ in (3.14) is more important than the drive due to ion–impurity friction, but both of these modifications are likely small in the Large Helical Device and Wendelstein 7-X, and will be yet smaller in a fusion reactor.
Table 1. Collisionality ![]() $\hat{\unicode[STIX]{x1D708}}_{ii}a/v_{Ti}$ calculated for different scenarios.
$\hat{\unicode[STIX]{x1D708}}_{ii}a/v_{Ti}$ calculated for different scenarios. ![]() $Z_{u}\equiv 0.3v_{Ti}/(\hat{\unicode[STIX]{x1D708}}_{ii}a)$ refers to the charge number at which impurity–ion collisions are expected to have an order-unity effect on the flux due to parallel compressibility (3.17). The parameters are taken form the following scenarios: W7-X – LBO impurity study (Langenberg et al. Reference Langenberg, Wegner, Pablant, Marchuk, Geiger, Tamura, Bussiahn, Kubkowska, Mollén and Traverso2020); TJ-II – LBO impurity study (Zurro et al. Reference Zurro, Hollmann, Baciero, Ochando, McCarthy, Medina, Velasco, Pastor, Baião and de la Cal2014); LHD – TESPEL impurity study (Tamura et al. Reference Tamura, Sudo, Suzuki, Funaba, Nakamura, Tanaka, Yoshinuma and Ida2016). In
$Z_{u}\equiv 0.3v_{Ti}/(\hat{\unicode[STIX]{x1D708}}_{ii}a)$ refers to the charge number at which impurity–ion collisions are expected to have an order-unity effect on the flux due to parallel compressibility (3.17). The parameters are taken form the following scenarios: W7-X – LBO impurity study (Langenberg et al. Reference Langenberg, Wegner, Pablant, Marchuk, Geiger, Tamura, Bussiahn, Kubkowska, Mollén and Traverso2020); TJ-II – LBO impurity study (Zurro et al. Reference Zurro, Hollmann, Baciero, Ochando, McCarthy, Medina, Velasco, Pastor, Baião and de la Cal2014); LHD – TESPEL impurity study (Tamura et al. Reference Tamura, Sudo, Suzuki, Funaba, Nakamura, Tanaka, Yoshinuma and Ida2016). In ![]() $Z_{u}$ we used
$Z_{u}$ we used ![]() $k_{\Vert }a\sim k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim 0.3$ to obtain one estimate for both (3.15) and (3.16).
$k_{\Vert }a\sim k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim 0.3$ to obtain one estimate for both (3.15) and (3.16).

Including both of the impurity–ion collisional modifications, the parallel compressibility flux becomes
It is difficult to draw any detailed conclusions from this expression, as the ![]() $A\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D719}^{\ast }$ term causes the flux to both depend on the phase of the imaginary
$A\unicode[STIX]{x1D735}_{\Vert }\unicode[STIX]{x1D719}^{\ast }$ term causes the flux to both depend on the phase of the imaginary ![]() $\unicode[STIX]{x1D719}$ and the ion–impurity friction force, which are beyond the scope of this work.
$\unicode[STIX]{x1D719}$ and the ion–impurity friction force, which are beyond the scope of this work.
4 Summary and conclusions
We have included impurity–ion collisions in the calculation of the quasi-linear particle flux of highly charged impurities. The lack of collisions was thought to be one of the main shortcomings of previous analytical calculations (Helander & Zocco Reference Helander and Zocco2018), and it can indeed affect the impurity flux if the bulk-ion collisionality times the charge number of the impurity is not small. This effect could thus be significant in present day experiments, in particular experiments with low ion temperature, such as TJ-II, but is not expected to be important in a fusion reactor or in larger fusion experiments.
As this result was based on an expansion in the largeness of the impurity charge number, it is not applicable to species with low charge – such as carbon – at least not in a quantitative sense. Indeed, for electrons, collisions can have a large effect on the electron particle transport (Angioni et al. Reference Angioni, Peeters, Jenko and Dannert2005; Fülöp, Pusztai & Helander Reference Fülöp, Pusztai and Helander2008), especially at low ![]() $k_{y}\unicode[STIX]{x1D70C}_{i}$-values (Angioni et al. Reference Angioni, Candy, Fable, Maslov, Peeters, Waltz and Weisen2009), if the electron–ion collision frequency is comparable to the mode frequency and/or drift frequency. However, for a highly charged species, the distribution function is predominantly set by the local value of the electrostatic potential and its parallel derivative, and collisions have a small effect.
$k_{y}\unicode[STIX]{x1D70C}_{i}$-values (Angioni et al. Reference Angioni, Candy, Fable, Maslov, Peeters, Waltz and Weisen2009), if the electron–ion collision frequency is comparable to the mode frequency and/or drift frequency. However, for a highly charged species, the distribution function is predominantly set by the local value of the electrostatic potential and its parallel derivative, and collisions have a small effect.
There are a few extensions to this work that may modify the above conclusion.
Firstly, if the impurities are not a trace, their distribution would affect the electrostatic potential fluctuation through the quasi-neutrality equation, and the potential would have to be expanded in ![]() $Z^{-1}$. However, the effect of collisions would then be smaller, as impurity self-collisions would dominate over ion–impurity collisions, according to (3.3). Thus, the conclusions of this paper apply even more strongly to highly charged non-trace impurities, as noted in Pusztai et al. (Reference Pusztai, Mollén, Fülöp and Candy2013). Of course, impurities would also affect the turbulence itself, but such effects are beyond the scope of the present paper.
$Z^{-1}$. However, the effect of collisions would then be smaller, as impurity self-collisions would dominate over ion–impurity collisions, according to (3.3). Thus, the conclusions of this paper apply even more strongly to highly charged non-trace impurities, as noted in Pusztai et al. (Reference Pusztai, Mollén, Fülöp and Candy2013). Of course, impurities would also affect the turbulence itself, but such effects are beyond the scope of the present paper.
Secondly, if the background impurity density were to vary on the flux surface, the Maxwellian in (3.4) and (3.14) would weight different parts of the flux surface differently, which could affect the relative importance of the impurity–ion friction and the parallel electric field.
Lastly, collisions also play an important role in saturating nonlinear gyrokinetic turbulence (Krommes Reference Krommes1999; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Plunk, Quataert and Tatsuno2008), which has not been considered in this work.