Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T16:41:49.354Z Has data issue: false hasContentIssue false
  • English
  • Français

Implicit role of Cairns distributed ions and weak relativistic effects of electrons in the formation of dust acoustic waves in plasma

Published online by Cambridge University Press:  03 March 2016

Bhaben Chandra Kalita  and
Rekha Kalita
Bhaben Chandra Kalita
Affiliation:
Department of Mathematics, Gauhati University, Guwahati-781014, Assam, India
Rekha Kalita*
Affiliation:
Department of Mathematics, Gauhati University, Guwahati-781014, Assam, India
*
†Email address for correspondence: rekhakalita973@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this model of a dusty plasma, we have investigated dust acoustic waves consisting of electrons with weak relativistic effects, Cairns distributed cold ions and negatively charged mobile dust. Dust acoustic (DA) compressive and rarefactive solitons of various amplitudes are established. The parameter 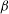${\it\beta}$ involved in Cairns distribution is related to the non-thermal parameter ${\it\alpha}$. However, the increase of 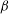${\it\beta}$, which is independent of temperature, becomes instrumental for complete linear increase or decrease of the amplitudes of both the compressive and rarefactive relativistic solitons. Hence it is worthwhile to note that the increase of 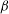${\it\beta}$ is solely due to the rest energy and not due to kinetic energy in this relativistic plasma. This is one of the most significant results of our investigation. Also, the flux of negative charges from the dust particles, together with the effect of the relativistic electrons, appears to balance the positive charges of Cairns distributed ions for nearly constant growth of amplitudes.

Type
Research Article
Information
Journal of Plasma Physics , Volume 82 , Issue 2 , April 2016 , 905820201
Check for updates
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ali, S. & Shukla, P. K. 2006 Dust acoustic solitary waves in a quantum plasma. Phys. Plasmas 13, 022313.Google Scholar
Asgari, H., Muniandy, S. V. & Wong, C. S. 2013 Dust-acoustic solitary waves in dusty plasmas with non-thermal ions. Phys. Plasmas 20, 023705.Google Scholar
Cairns, R. A., Mamun, A. A., Bingham, R., Dendy, R., Boström, R., Nairns, C. M. C. & Shukla, P. K. 1995 Electrostatic solitary structures in non-thermal plasmas. Geophys. Res. Lett. 22, 2709.Google Scholar
Choi, C. R., Lee, D.-Y., Kim, Y.-H. & Lee, C. 2009 Effects of charged dust particles on nonlinear ion acoustic solitary waves in a relativistic plasma. Phys. Plasmas 16, 043701.Google Scholar
Chow, V. W., Mendis, D. A. & Rosenberg, M. J. 1993 Role of grain size and particle velocity distribution in secondary electron emission in space plasmas. J. Geophys. Res. 98, 19065–19076.Google Scholar
Futaana, Y., Machida, S., Saito, Y., Matsuoka, A. & Hayakawa, H. 2001 Counterstreaming electrons in the near viscinity of the Moon observed by plasma instruments on board NOZOMI. J. Geophys. Res. 106, 18725–18740.Google Scholar
Haider, M. M., Ferdous, T., Duha, S. S. & Mamun, A. A. 2014 Dust-ion-acoustic solitary waves in multi-component magnetized plasmas. Open. Jr. Mod. Phys. 1, 2372.Google Scholar
Kalita, B. C. & Choudhury, M. 2013 The role of unidirected relativistic electrons with inertia in the formation of weakly relativistic ion acoustic solitons in magnetized plasma. Astrophys. Space Sci. 346, 375–382.Google Scholar
Kalita, B. C. & Das, S. 2014 Dust ion acoustic (DIA) solitary waves in plasmas with weak relativistic effects in electrons and ions. Astrophys. Space Sci. 352, 585–592.Google Scholar
Kalita, B. C. & Deka, M. 2013 Investigation of solitary waves in warm plasma for smaller order relativistic effects with variable pressures and inertia of electrons. Astrophys. Space Sci. 343 (2), 609–614.Google Scholar
Kalita, B. C. & Kalita, R. 2015 A new approach to energy integral for investigation of dust–ion acoustic (DIA) waves in multi-component plasmas with quantum effects in inertia less electrons. Commun. Theor. Phys. 63, 761–768.Google Scholar
Kundu, N. R., Masud, M. M., Ashraf, K. S. & Mamun, A. A. 2013 Dust-ion-acoustic solitary waves and their multi-dimensional instability in a magnetized nonthermal dusty electronegative plasma. Astrophys. Space Sci. 343, 279–287.Google Scholar
Liu, H. F., Wang, S. Q., Li, C. Z., Xiang, Q., Yang, F. Z. & Liu, Y. 2010 Cylindrical and spherical dust-ion acoustic solitary waves in a relativistic dust plasma. Phys. Scr. 82, 065402.CrossRefGoogle Scholar
Liu, H. F., Wang, S. Q., Wang, Z., Yang, F. Z., Liu, Y. & Li, S. 2013 Propagation of cylindrical and spherical dust-ion-acoustic solitary waves in a relativistic dusty plasma. Adv. Space Res. 51, 2368–2373.CrossRefGoogle Scholar
Lundin, R., Zakharov, A., Pellinen, R., Borg, H., Hultqvist, B., Pissarenko, N., Dubinin, E. M., Barabash, S. W., Liede, I. & Koskinen, H. 1989 First measurements of the ionospheric plasma escape from Mars. Nature 341 (6243), 609–612.Google Scholar
Mamun, A. A. 1998 Nonlinear propagation of dust-acoustic waves in a magnetized dusty plasma with vortex-like ion distribution. J. Plasma Phys. 59, 575–580.CrossRefGoogle Scholar
Mamun, A. A., Cairns, R. A. & D’Angelo, N. 1996 Effects of vortex-like and non-thermal ion distributions on non-linear dust-acoustic waves. Phys. Plasmas 3 (7), 2610.Google Scholar
Masud, M. M., Asaduzzaman, M. & Mamun, A. A. 2012 Dust-ion-acoustic Gardner solitons in a dusty plasma with bi-Maxwellian electrons. Phys. Plasma 19, 103706.CrossRefGoogle Scholar
Mendis, D. A.2005 Dust–plasma interactions in space in New Vistas in Dusty plasmas. In 4th International Conference’ Physics of Dusty Plasmas.Google Scholar
Mendis, D. A. & Rosenberg, M. 1994 Cosmic dusty plasma. Annu. Rev. Astron. Astrophys. 32, 419–463.Google Scholar
Misra, A. P. & Chowdhury, A. R. 2006 Modulation of dust acoustic waves with a quantum correction. Phys. Plasmas 13, 072305.CrossRefGoogle Scholar
Moslem, W. M., Shukla, P. K., Ali, S. & Schlickeiser, R. 2007 Quantum dust-acoustic double layers. Phys. Plasmas 14, 042107.Google Scholar
Pakzad, H. R. 2009 Dust acoustic solitary waves in dusty plasma with nonthermal ions. Astrophys. Space Sci. 324, 41–45.Google Scholar
Rao, N. N., Shukla, P. K. & Yu, M. Y. 1990 Dust-acoustic waves in dusty plasmas. Planet. Space Sci. 38, 543–546.Google Scholar
Rosenberg, M. 1993 Ion-and dust-acoustic instabilities in dusty plasmas. Planet. Space Sci. 41, 229–233.Google Scholar
Shukla, P. K. & Mamun, A. A. 2002 Introduction to Dusty Plasma Physics. IOP.Google Scholar
Shukla, P. K. & Silin, V. P. 1992 Dust ion-acoustic wave. Phys. Scr. 45, 508.CrossRefGoogle Scholar
Tokar, R. L. & Gary, S. P. 1984 Electrostatic hiss and the beam driven electron acoustic instability in the dayside polar cusp. Geophys. Res. Lett. 11, 1180–1183.Google Scholar
Verheest, F. 2000 Waves in Dusty Space Plasmas. Kluwer Academic.Google Scholar
Verheest, F. & Heillberg, M. 2009 Comment on ‘Effects of charged dust particles on nonlinear ion acoustic solitary waves in a relativistic plasma’. Phys. Plasmas 16 (6), 064701.Google Scholar
Verheest, F. & Pillay, S. R. 2008a Large amplitude dust-acoustic solitary waves and double layers in nonthermal plasmas. Phys. Plasmas 15, 013703.Google Scholar
Verheest, F. & Pillay, S. R. 2008b Dust-acoustic solitary structures in plasmas with nonthermal electrons and positive dust. Nonlinear Process. Geophys. 15, 551–555.CrossRefGoogle Scholar
Vette, J. I. 1970 Summary of Particle Population in the Magnetosphere, vol. 17, pp. 305–318. Reidel.Google Scholar
Yaroshenko, V. V., Verheest, F. & Morfill, G. E. 2007 Dust-acoustic waves in collisional dusty plasmas of planetary rings. Astron. Astrophys. 461, 385–391.Google Scholar
Zhao, Y., Zheng, J., Chen, M., Yu, L.-L., Weng, S.-M., Ren, C., Liu, C.-S. & Sheng, Z.-M. 2014 Effects of relativistic electron temperature on parametric instabilities for intense laser propagation in underdense plasma. Phys. Plasmas 21, 112114.Google Scholar