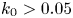Modulational instability of the interacting electron whistlers and magnetosonic perturbations

Abstract

A modulational instability of nonlinearly interacting electron whistlers and magnetosonic perturbations is studied in the present paper. For typical parameters, there is no modulational instability. However, modulational instability appears in special cases. For example, when the whistler wavenumber is small enough, there is modulational instability. Its growth rate decreases as the angle between the external magnetic field and the perturbed wave's direction increases, while it increases as the whistler wavenumber increases. It is also found that there is no modulational instability when the whistler wavenumber is larger than a critical value ($k_0 > 0.05$), in which the perturbed wave frequency increases as the angle between the external magnetic field and the perturbed wave's direction increases when the angle between the external magnetic field and the perturbed wave's direction is large enough. Whereas, the perturbed wave frequency first increases as the whistler wavenumber increases, reaches a peak value and then decreases as whistler wavenumber increases.

1. Introduction

Whistler waves are commonly observed phenomena in both space plasma and laboratory plasma (Stenzel 1999). They are a special type of electromagnetic wave found in various plasma environments, including atmospheric lightning, intense particle flows, magnetospheric turbulence, shock waves and even antennas in laboratory experiments. The formation of whistler waves involves multiple factors in plasma physics, such as electron beams, magnetic field instability and magnetic reconnection (Fujimoto & Sydora 2008; Choi et al. 2022). Non-thermal whistler waves are a unique type of electromagnetic wave propagating in plasmas, primarily along geomagnetic field lines, playing a crucial role in fast magnetic reconnection processes. Particularly in the presence of sheared magnetic fields, two-dimensional whistler waves demonstrate remarkable abilities, serving as a medium to facilitate fast magnetic reconnection (Li et al. 2014; Li, Wang & Lu 2023), a fundamental process in rapidly rearranging magnetic field lines. This process is essential for the energization and acceleration of electrons in the plasma (Hoshino et al. 2001). Simultaneously, the energy released during magnetic reconnection may excite two-dimensional whistler waves, and the presence of these waves can, in turn, influence the dynamical evolution of magnetic reconnection (Bell et al. 2002; Horne et al. 2005). This interaction involves energy release, dynamical evolution and potential observation of nonlinear effects, contributing significantly to a deeper understanding of wave phenomena and magnetic field structure evolution in plasmas.

In plasma physics, whistler waves and magnetosonic perturbations play a crucial role in understanding the complex dynamics of space and laboratory plasmas. Extensive scholarly research has been dedicated to unravelling the intricate properties and behaviours of whistler waves. Notably, a recent laboratory experiment employed a non-stationary magnetic field (Kostrov et al. 2003; Gushchin et al. 2004), yielding significant insights into the self-focusing phenomenon exhibited by whistlers propagating parallel to the magnetic field direction (Karpman & Shagalov 1984; Karpman, Kaufman & Shagalov 1992; Eliasson & Shukla 2005a; Gupta, Choudhry & Bhardwaj 2023). This unique behaviour resulted in the formation of isolated wave packets (Gaster & Grant 1975). Experiments also have revealed the capture of whistlers within ducts characterized by depleted plasma density, highlighting the interplay between wave propagation and plasma density variations (Nassiri 2008; Singh 2013). Moreover, the confinement of whistlers within magnetic tubes, characterized by localized regions of enhanced magnetic fields in a uniform plasma density environment, has been experimentally demonstrated (Gushchin et al. 2005). Additionally, the generation of electrostatic ion cyclotron waves has been observed in large-volume spiral reactors, indicative of the parametric instability associated with high-amplitude whistlers (Sutherland, Giles & Boswell 2005; Tripathi & Kumara 2008). Findings from the Freja satellite (Huang, Wang & Song 2004) also reveal the occurrence of envelope whistler solitary waves accompanied by plasma density cavities.

Modulational instability refers to the phenomenon in nonlinear systems where, due to the interaction between nonlinear effects and dispersion effects, plane waves undergo filamentation under high-intensity conditions. This results in small-amplitude perturbations experiencing exponential growth, ultimately leading to the modulation or formation of spatial structures in the wave (Inan 1987; Meier et al. 2004; Shukla et al. 2005). Modulational instability is widely observed in various fields of physics, including fluid dynamics, nonlinear optics and plasma physics. Therefore, investigating the development of modulational instability and its propagation in plasmas holds significant importance (Gurovich & Karpman 1969; Tai, Hasegawa & Tomita 1986; Kivshar 1992). Considering the mass potential of spatiotemporal correlation in whistler waves (Tskhakaya 1981; Zhu et al. 2023), the modulational instability of nonlinearly interacting electron whistlers and magnetosonic perturbations is studied in the present paper (Karpman et al. 1995; Das et al. 2002). It is found that, for typical plasma parameters, there is no modulational instability. However, modulational instability appears in special cases. It is shown that when the whistler wavenumber is small enough, there is modulational instability. It is also found that there is no modulational instability when the whistler wavenumber is larger than a critical value.

The content of the paper is organized as follows. In § 2, the coupled nonlinear equations which describe the dynamics of the whistler envelope in the presence of the slowly varying magnetic field have been presented. Section 3 obtains solutions for background and perturbation waves. Section 4 discusses various special cases. Section 5 establishes the instability conditions for perturbation waves and § 6 provides a summary and conclusions.

2. Theoretical model

We start by obtaining the relevant equations for nonlinearly coupled whistlers and magnetosonic perturbations in a fully ionized electron–ion plasma. The fundamental equations for the plasma slow response concerning magnetosonic disturbances can be expressed as follows (Eliasson & Shukla 2005b):

(2.1)\begin{gather} \frac{\partial n_1 }{\partial t} +n_0\boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{v_1}=0, \end{gather}

(2.2)\begin{gather}\frac{\partial \boldsymbol{v_1} }{\partial t} ={-}\frac{C_s^2 \boldsymbol{\nabla} n_1 }{n_0} -\frac{1 }{4{\rm \pi} m_in_0}\boldsymbol{B}_{\boldsymbol{0}}\times (\boldsymbol{\nabla} \times \boldsymbol{B}_{\boldsymbol{1}}) + \frac{\boldsymbol{F} }{m_i}, \end{gather}

(2.3)\begin{gather}\frac{\partial \boldsymbol{B}_{\boldsymbol{1}} }{\partial t} -\boldsymbol{\nabla}\times (\boldsymbol{v_1}\times\boldsymbol{B}_{\boldsymbol{0}})=0. \end{gather}

The total quantities for ion density, ion fluid velocity and magnetic field can be expressed as follows: $n=n_0+n_1$, $\boldsymbol {B}=\boldsymbol {B}_0+\boldsymbol {B}_1$; where $n$ is the total electron number density, $n_1$ is the electron density perturbation, $\boldsymbol {B}$ is the total magnetic field vector, $\boldsymbol {B}_{\boldsymbol {1}}$ is the magnetic field perturbation, $\boldsymbol {v}_{\boldsymbol {1}}$ is the velocity, $n_0$ denotes the electron number density in the absence of any perturbations, $\boldsymbol {B}_{\boldsymbol {0}} = B_0\hat {\boldsymbol {z}}$ represents the uniform magnetic field in the direction of $z$, where $\hat {\boldsymbol {z}}$ is a unit vector along the $z$ axis, $C_s$ is the speed of ion acoustic waves, $m_i$ is the mass of ions.

The ponderomotive force associated with whistler waves can be expressed as follows:

(2.4)\begin{equation} \boldsymbol{F} =\hat{\boldsymbol{z}}\epsilon\left(\frac{\partial }{\partial z}+ \frac{2 }{V_g}\frac{\partial }{\partial t}\right) \frac{| E|^2 }{8{\rm \pi} n_0}-\frac{\epsilon \alpha }{1-\alpha} \boldsymbol{\nabla}_\bot \frac{| E|^2 }{8{\rm \pi} n_0}, \end{equation}

the differentiation operator in this context is defined as $\boldsymbol {\nabla }_\bot =\hat {\boldsymbol {x}}{\partial / \partial x}+\hat {\boldsymbol {y}}{\partial / \partial y}$, where $\hat {\boldsymbol {x}}$ and $\hat {\boldsymbol {y}}$ are unit vectors along the $x$ and $y$ directions, respectively. Additionally, the following parameters are defined: $\epsilon ={\omega _{{\rm pe}}^2 / \omega _0(\omega _{{\rm ce}}-\omega _0)}$ and $\alpha ={\omega _0 / \omega _{{\rm ce}}}$; where $\omega _{{\rm pe}}$ is the electron plasma frequency, $\omega _{{\rm ce}}$ is the electron cyclotron frequency and $\omega _0$ is the whistler waves frequency. The frequency of whistler waves with wavenumber $k_0$ is given by $\omega _0=c^2k_0^2\omega _{{\rm ce}}/(\omega _{{\rm pe}}^2+c^2k_0^2)$, where $c$ is the speed of light in a vacuum.

These equations can be further simplified to study the behaviour of nonlinearly coupled whistlers and magnetosonic perturbations in an electron–ion plasma. By eliminating the perpendicular components of the magnetic field, $B_{1x}$ and $B_{1y}$, and velocity, $v_{1x}$ and $v_{1y}$, the system of equations (2.1)–(2.3) can be given by

(2.5)\begin{gather} \frac{\partial^2 b}{\partial t^2}=C_s^2\nabla_\bot^2N +C_A^2\left(\nabla_\bot^2+ \frac{\partial^2}{\partial z^2}\right)b + \frac{\epsilon \alpha }{1-\alpha}\nabla_\bot^2\frac{| E|^2}{8{\rm \pi} m_in_0}, \end{gather}

(2.6)\begin{gather}\frac{\partial }{\partial t}(N-b)={-}\frac{\partial v_{1z} }{\partial z}, \end{gather}

(2.7)\begin{gather}\frac{\partial v_{1z} }{\partial t} ={-}C_s^2 \frac{\partial N }{\partial z}+\epsilon \left(\frac{\partial }{\partial z}+\frac{2 }{V_g}\frac{\partial }{\partial t}\right) \frac{| E|^2 }{8{\rm \pi} m_in_0}, \end{gather}

where $C_A={B_0 / {(4{\rm \pi} m_in_0)}^{1/2}}$ is the Alfvén speed; and we have denoted $b={B_{1z} / B_0}$ and $N={n_1 / n_0}$.

We now focus on the modulated whistlers with right-hand circular polarization and assume that $\boldsymbol {E}={(1/2)}E(x,y,z,t)(\hat {\boldsymbol {x}}+{\rm i}\hat {\boldsymbol {y}})\exp {[{\rm i}(k_0z-\omega _0t)]}+c.c.$, where $E$ represents the slowly varying envelope of the whistler electric field and $c.c.$ denotes the complex conjugate. The equation governing the whistler field envelope is given by (Shukla & Stenflo 1995)

(2.8)\begin{equation} {\rm i}\left(\frac{\partial E }{\partial t}+ V_g\frac{\partial E }{\partial z}\right)+ \frac{V_g' }{2}\frac{\partial^2 E }{\partial z^2}+\frac{T }{2} \nabla_\bot^2E +\{\omega_0[(1-\alpha)N-b]-k_0v_{1z}\} E=0, \end{equation}

where $V_g={2(1-\alpha )\omega _0 / k_0}$ is the group velocity, $V_g'={2(1-\alpha )(1-4\alpha )\omega _0 / k_0^2}$ and $T={ (1-2\alpha ) \omega _0 / k_0^2}$ are the group dispersion coefficients. Notice that $V_g$, $V_g'$ and $T$ can change sign depending on the ratio $\alpha$, which is critical for the formation of localized nonlinear wave packets at different frequencies. The $k_0v_{1z}$ term represents the Doppler shift due to the plasma streaming along the magnetic field.

In the special case where the wave packet is modulated along the $z$ axis and moving at a speed close to the group velocity $V_g$, we can make certain assumptions to simplify the equations. Assuming $b=0$ and $N$ depends only on $\xi =z-V_gt$, we can integrate (2.6) to obtain $v_{1z}=NV_g$, and subsequently, $k_0v_{1z}=2\omega _0(1-\alpha )N$.

Assuming that $N$, $b$, $v_{1z}$ and $| E|$ are functions of the variables $(\xi, \boldsymbol {x}_\bot, \tau )$, where $\tau =t$ and that ${\partial / \partial \tau }<<{\partial / \partial \xi }$, (2.6)–(2.8) can be rewritten as follows:

(2.9)\begin{gather} V_g^2\frac{\partial^2 b}{\partial \xi^2} =C_s^2\nabla_\bot^2N +C_A^2\left(\nabla_\bot^2+ \frac{\partial^2}{\partial \xi^2}\right)b +\frac{\epsilon \alpha }{1-\alpha}\nabla_\bot^2\frac{| E|^2}{8{\rm \pi} m_in_0}, \end{gather}

(2.10)\begin{gather}-V_g \frac{\partial }{\partial \xi}(N-b)={-}\frac{\partial v_{1z} }{\partial \xi}, \end{gather}

(2.11)\begin{gather}-V_g \frac{\partial v_{1z} }{\partial \xi} ={-}C_s^2 \frac{\partial N }{\partial \xi}-\epsilon \frac{\partial }{\partial \xi}\frac{| E|^2 }{8{\rm \pi} m_in_0}. \end{gather}

By integrating (2.10) and (2.11), we have $V_g(N-b)=v_{1z}$ and $V_gv_{1z}=C_s^2N+\epsilon {| E|^2 / 8{\rm \pi} m_in_0}$, then, (2.9) becomes

(2.12)\begin{equation} \frac{\partial^2 b }{\partial \xi^2}-\nu^2 \nabla_\bot^2b = Q\epsilon \nabla_\bot^2 \frac{| E|^2 }{8{\rm \pi} m_in_0}, \end{equation}

where $\nu ^2=[{C_s^2V_g^2 / (V_g^2-C_s^2)}+C_A^2] / (V_g^2-C_A^2)$ and $Q=[{C_s^2 / (V_g^2-C_s^2)}+{\alpha / (1-\alpha )}] / (V_g^2-C_A^2)$. Furthermore, (2.8) becomes

(2.13)\begin{equation} {\rm i} \frac{\partial E }{\partial \tau} +\frac{V_g'}{2} \frac{\partial^2 E}{\partial \xi^2}+\frac{T }{2} \nabla_\bot^2E -\frac{\omega_0}{V_g^2-C_s^2}\left\{[\alpha V_g^2+(1-2\alpha)C_s^2]b +(1-\alpha)\epsilon\frac{| E|^2 }{8{\rm \pi} m_in_0}\right\}E=0. \end{equation}

Equations (2.12) and (2.13) are the coupled nonlinear equations which describes the dynamics of the whistler envelope in the presence of the slowly varying magnetic field.

3. Instability of the whistler envelope waves

3.1. Linear background wave

To understand the linear background wave, we make the assumptions $E=a_0\exp ({{\rm i}\theta _0(\tau )})$, $G=d_0\exp ({{\rm i}\beta _0(\tau )})$, $b=| G |^2$, where $a_0$ and $d_0$ are constants. Consequently, we obtain $| E|^2=a_0^2$, $b=d_0^2$, ${\nabla }_\bot ^2b=0$. Additionally, we have ${\nabla }_\bot ^2E=0$, ${\partial ^2 b / \partial \xi ^2}=0$, ${\partial ^2 E / \partial \xi ^2}=0$, ${\partial E / \partial \tau }={\rm i}E{\partial \theta _0 / \partial \tau }$, ${\partial ^2 E /\partial \tau ^2} = - E{ ({\partial \theta _0 / \partial \tau }) ^2} + {\rm i}E{{\partial ^2} \theta _0 /\partial {\tau ^2}}$. After substituting these equations into (2.12) and (2.13), we have

(3.1)\begin{equation} {\theta _0(\tau)}={-}\frac{\omega_0 \tau }{V_g^2-C_s^2} \left\{[\alpha V_g^2+(1-2\alpha)C_s^2]d_0^2 +(1-\alpha)\epsilon\frac{a_0^2 }{8{\rm \pi} m_in_0}\right\}. \end{equation}

Then, we have

(3.2)\begin{gather} E = a_0{\exp\left({-{\rm i}\frac{\omega _0 }{V_g^2 - C_s^2} \left\{{[{\alpha V_g^2 + (1 - 2\alpha)C_s^2}]d_0^2 + (1 - \alpha) \epsilon \frac{c_0^2 }{8{\rm \pi} m_in_0}}\right\} \tau}\right)}, \end{gather}

(3.3)\begin{gather}b = d_0^2. \end{gather}

Equations (3.2) and (3.3) represent the linear background wave. Its frequency is

(3.4)\begin{equation} \omega_{bc}=\frac{\omega _0 }{V_g^2 - C_s^2}\left\{{[ {\alpha V_g^2 + (1 - 2\alpha)C_s^2}]d_0^2 + (1 - \alpha) \epsilon \frac{a_0^2 }{8{\rm \pi} m_in_0}}\right\}. \end{equation}

3.2. Nonlinear wave

For more general case of the nonlinear wave, we assume

(3.5)\begin{gather} E(x,y,\xi ,\tau) = a(x,y,\xi,\tau) \exp{[{\rm i}\theta(x,y,\xi ,\tau)]}, \end{gather}

(3.6)\begin{gather}G(x,y,\xi ,\tau) = d(x,y,\xi ,\tau)\exp{[{\rm i}\beta(x,y,\xi , \tau)]}, \end{gather}

(3.7)\begin{gather}b(x,y,\xi ,\tau) =| G(x,y,\xi ,\tau) |^2. \end{gather}

Then we have $| E|^2=| a(x,y,\xi,\tau )|^2$, $b=| d(x,y,\xi,\tau )|^2$, and the following equations:

(3.8)\begin{equation} \frac{\partial^2 | d | ^2 }{\partial \xi ^2} - {\nu ^2} \left(\frac{\partial ^2 | d | ^2}{\partial x^2} + \frac{\partial ^2 | d | ^2 }{\partial y^2}\right) = Q \epsilon \frac{\dfrac{\partial ^2 | a |^2}{\partial x^2}+ \dfrac{\partial ^2 | a | ^2 }{\partial y^2}}{8{\rm \pi} m_in_0}, \end{equation}

(3.9)\begin{align} & {\rm i}\left(\frac{\partial a }{\partial \tau} + {\rm i}a\frac{\partial \theta }{\partial \tau}\right)+ \frac{V_g'}{2}\left[\frac{\partial ^2a }{\partial \xi ^2}+ 2{\rm i}\frac{\partial a }{\partial \xi } \frac{\partial\theta }{\partial \xi }- a{\left(\frac{\partial \theta }{\partial \xi }\right)^2}+ {\rm i}a\frac{\partial ^2 \theta}{\partial \xi ^2}\right] +\frac{T }{2} \left\{\frac{\partial ^2a }{\partial x^2} + \frac{\partial ^2a}{\partial y^2} \vphantom{\left[{\left(\frac{\partial \theta}{\partial x}\right)^2} + {\left(\frac{\partial \theta}{\partial y}\right)^2}\right]}\right.\nonumber\\ & \quad \left.+ 2{\rm i}\left(\frac{\partial a}{\partial x} \frac{\partial \theta}{\partial x} + \frac{\partial a}{\partial y} \frac{\partial \theta}{\partial y}\right)- a\left[{\left(\frac{\partial \theta}{\partial x}\right)^2} + {\left(\frac{\partial \theta}{\partial y}\right)^2}\right] +{\rm i}a\left(\frac{\partial ^2 \theta}{\partial x^2} + \frac{\partial ^2 \theta}{\partial y^2}\right)\right\} \nonumber\\ & \quad - \frac{a\omega_0}{V_g^2-C_s^2} \left\{[\alpha V_g^2+(1-2\alpha)C_s^2]| d |^2 +(1-\alpha)\epsilon\frac{| a |^2}{8{\rm \pi} m_in_0}\right\}=0. \end{align}

We obtain two equations from both real and imaginary terms of (3.9) as follows:

(3.10)\begin{align} & - a\frac{\partial \theta }{\partial \tau}+\frac{V_g' }{2} \frac{\partial ^2a }{\partial \xi ^2}- \frac{aV_g'^2 }{2} {\left(\frac{\partial \theta }{\partial \xi }\right)^2}+\frac{T }{2} \frac{\partial ^2a }{\partial x^2} + \frac{T }{2}\frac{\partial ^2a }{\partial y^2} - \frac{aT }{2}{\left(\frac{\partial \theta }{\partial x}\right)^2} \nonumber\\ & \quad -\frac{aT}{2}{\left(\frac{\partial \theta}{\partial y}\right)^2} - \frac{a\omega_0}{V_g^2-C_s^2} \left\{[\alpha V_g^2 +(1-2\alpha)C_s^2]| d |^2+(1-\alpha) \epsilon\frac{| a|^2}{8{\rm \pi} m_in_0}\right\}=0, \end{align}

(3.11)\begin{align} & \frac{\partial a }{\partial \tau} + V_g'\frac{\partial a }{\partial \xi } \frac{\partial \theta }{\partial \xi }+ \frac{aV_g' }{2} \frac{\partial ^2 \theta }{\partial \xi ^2}+ T\frac{\partial a }{\partial x} \frac{\partial \theta }{\partial x}+ T\frac{\partial a }{\partial y} \frac{\partial \theta }{\partial y}+\frac{aT }{2} \frac{\partial ^2 \theta }{\partial x^2} +\frac{aT }{2} \frac{\partial ^2 \theta }{\partial y^2}=0. \end{align}

We rewrote (3.8) as follows:

(3.12)\begin{equation} \frac{\partial ^2 | d | ^2 }{\partial \xi ^2} - {\nu ^2} \left(\frac{\partial ^2 | d | ^2 }{\partial x^2} + \frac{\partial ^2 | d | ^2 }{\partial y^2}\right) = Q \epsilon \frac{\dfrac{\partial ^2 | a |^2 }{\partial x^2}+ \dfrac{\partial ^2 | a | ^2 }{\partial y^2}}{8{\rm \pi} m_in_0}. \end{equation}

Further, we assume that

(3.13)\begin{gather} a(x,y,\xi ,\tau)= a_0(\tau) + \varepsilon a_1(x,y,\xi ,\tau), \end{gather}

(3.14)\begin{gather}d(x,y,\xi ,\tau)= d_0(\tau) + \varepsilon d_1(x,y,\xi ,\tau), \end{gather}

(3.15)\begin{gather}\theta(x,y,\xi ,\tau)= \theta_0(\tau) + \varepsilon \theta_1(x,y,\xi ,\tau), \end{gather}

where all the variables are complex, as later indicated by their complex conjugates.

Then (3.10)–(3.12) become

(3.16)\begin{align} & (a_0 + \varepsilon a_1)\left(\frac{\partial \theta _0 }{\partial \tau} + \varepsilon \frac{\partial \theta _1 }{\partial \tau}\right) +\frac{\varepsilon ^2 V_g' }{2}(a_0 + \varepsilon a_1) {\left(\frac{\partial \theta _1 }{\partial \xi}\right)^2}+ \frac{\varepsilon ^2T }{2}(a_0 + \varepsilon a_1){\left(\frac{\partial \theta _1 }{\partial x}\right)^2} \nonumber\\ & \quad +\frac{\varepsilon ^2T}{2}(a_0 + \varepsilon a_1) {\left(\frac{\partial \theta _1}{\partial y}\right)^2} -\frac{\varepsilon V_g'}{2}\frac{\partial^2a_1}{\partial \xi ^2}- \frac{\varepsilon T}{2}\frac{\partial ^2a_1}{\partial x^2} - \frac{\varepsilon T}{2}\frac{\partial ^2a_1}{\partial y^2} \nonumber\\ & \quad + \frac{\omega _0}{V_g^2 - C_s^2}(a_0 + \varepsilon a_1) [{\alpha V_g^2 + ( 1 - 2\alpha )C_s^2} ] [{{| d_0 | ^2} + \varepsilon (d_0d_1^ * + d_1d_0^ * ) + {\varepsilon ^2}{| d_1 | } ^2}] \nonumber\\ & \quad +\frac{\omega _0}{V_g^2 - C_s^2}(a_0 + \varepsilon a_1)( 1 - \alpha ) \epsilon \frac{1}{8{\rm \pi} m_in_0} [ {{| a_0 | ^2} + \varepsilon (a_0a_1^ * + a_1a_0^ * ) {\varepsilon ^2}{| a_1 | } ^2}]=0, \end{align}

(3.17)\begin{align} & \frac{a_0}{\partial \tau} + \varepsilon \frac{\partial a_1 }{\partial \tau} + {\varepsilon ^2 V_g'} \frac{\partial a_1 }{\partial \xi }\frac{\partial \theta _1 }{\partial \xi } + \varepsilon \frac{a_0V_g' }{2}\frac{\partial ^2 \theta _1 }{\partial \xi ^2}+ \varepsilon ^2 \frac{a_1V_g' }{2}\frac{\partial ^2 \theta _1 }{\partial \xi ^2} + {\varepsilon ^2 T} \frac{\partial a_1 }{\partial x}\frac{\partial \theta _1 }{\partial x} \nonumber\\ & \quad + {\varepsilon ^2T}\frac{\partial a_1}{\partial y} \frac{\partial \theta _1}{\partial y}+{\varepsilon} \frac{a_0T}{2} \frac{\partial ^2 \theta _1}{\partial x^2} + \varepsilon ^2 \frac{a_1T}{2}\frac{\partial ^2 \theta_1}{\partial x^2} + \varepsilon \frac{a_0T}{2}\frac{\partial^2\theta _1}{\partial y^2} + \varepsilon ^2 \frac{a_1T}{2}\frac{\partial ^2 \theta _1}{\partial y^2}=0, \end{align}

(3.18)\begin{align} & {\varepsilon d_0}\frac{\partial ^2d_1^ * }{\partial \xi ^2} + \varepsilon d_0^ * \frac{\partial ^2d_1 }{\partial \xi ^2} + {\varepsilon ^2} \frac{\partial ^2 | d_1 | ^2 }{\partial \xi ^2} - {\varepsilon \nu ^2 d_0} \frac{\partial ^2d_1^ * }{\partial x^2} - {\varepsilon \nu ^2d_0^ *} \frac{\partial ^2d_1 }{\partial x^2}- {\varepsilon ^2\nu ^2} \frac{\partial ^2 | d_1 | ^2 }{\partial x^2} \nonumber\\ & \quad -{\varepsilon \nu ^2d_0}\frac{\partial ^2d_1^ *}{\partial y^2} - {\varepsilon \nu ^2d_0^ *}\frac{\partial ^2d_1}{\partial y^2} - {\varepsilon ^2 \nu ^2}\frac{\partial ^2 | d_1 | ^2}{\partial y^2} - \varepsilon \frac{Qa_0 \epsilon}{8{\rm \pi} m_in_0}\frac{\partial ^2a_1^ *}{\partial x^2} - \varepsilon \frac{Qa_0^ * \epsilon}{8{\rm \pi} m_in_0} \frac{\partial ^2a_1}{\partial x^2} \nonumber\\ & \quad - {\varepsilon ^2}\frac{Q \epsilon}{8{\rm \pi} m_in_0} \frac{\partial ^2 | a_1 | ^2}{\partial x^2}- \varepsilon \frac{Qa_0 \epsilon}{8{\rm \pi} m_in_0} \frac{\partial^2a_1^*}{\partial y^2} - \varepsilon\frac{Qa_0^ * \epsilon}{8{\rm \pi} m_in_0} \frac{\partial^2a_1}{\partial y^2} - {\varepsilon ^2} \frac{Q\epsilon}{8{\rm \pi} m_in_0}\frac{\partial ^2 | a_1 | ^2}{\partial y^2}=0. \end{align}

The solutions for the lowest order ${\varepsilon ^0}$ of (3.16)–(3.18) are as follows:

(3.19)\begin{gather} {\theta _0 (\tau)} ={-}\left[\frac{\omega _0 \alpha V_g^2 | d_0 | ^2 }{{V_g^2 - C_s}} + \frac{\omega _0 (1-2\alpha) C_s^2 | d_0 | ^2 }{{V_g^2 - C_s^2}} +\frac{ \epsilon \omega _0 (1-\alpha) | a_0 | ^2 }{{8{\rm \pi} m_in_)} (V_g^2 - C_s^20)}\right]\tau, \end{gather}

(3.20)\begin{gather}{a_0(\tau)}={E_{00}}, \end{gather}

where $E_{00}$ is any arbitrary constant and we assumed that ${a_0 = 1}$ in the numerical simulations.

We have the following equations at the next lowest order of ${\varepsilon ^1}$:

(3.21)\begin{align} & a_0\frac{\partial \theta _1 }{\partial \tau} + a_1 \frac{\partial \theta _0 }{\partial \tau} - \frac{V_g' }{2} \frac{\partial ^2a_1 }{\partial \xi ^2} - \frac{T }{2} \frac{\partial ^2a_1 }{\partial x^2} - \frac{T }{2}\frac{\partial ^2a_1 }{\partial y^2} + \frac{a_0\omega _0 \alpha V_g^2d_0d_1^ * }{V_g^2 - C_s^2} \nonumber\\ & \quad + \frac{a_0\omega _0 \alpha V_g^2d_1d_0^ *}{V_g^2 - C_s^2} + \frac{a_1\omega _0 \alpha V_g^2 | d_0 | ^2}{V_g^2 - C_s^2} + \frac{a_0\omega _0C_s^2d_0d_1^ *}{V_g^2 - C_s^2} + \frac{a_0\omega _0C_s^2d_1d_0^*}{V_g^2 - C_s^2} \nonumber\\ & \quad + \frac{a_1\omega _0C_s^2 | d_0 | ^2}{V_g^2 - C_s^2} - \frac{2a_0\alpha \omega _0C_s^2d_0d_1^ *}{V_g^2 - C_s^2} - \frac{2a_0\alpha \omega _0C_s^2d_1d_0^ *}{V_g^2 - C_s^2} - \frac{2a_1\alpha \omega_0C_s^2 | d_0 | ^2}{V_g^2 - C_s^2} \nonumber\\ & \quad + \frac{\epsilon \omega _0a_0^2a_1^ *}{V_g^2 - C_s^2} \frac{1}{8{\rm \pi} m_in_0} + \frac{\epsilon | a_0 | ^2\omega _0a_1}{V_g^2 - C_s^2} \frac{1}{8{\rm \pi} m_in_0} + \frac{\epsilon a_1\omega _0 | a_0 | ^2}{V_g^2 - C_s^2} \frac{1}{8{\rm \pi} m_in_0} \nonumber\\ & \quad - \frac{\alpha \omega _0 \epsilon a_0^2a_1^ *}{V_g^2 - C_s^2} \frac{1}{8{\rm \pi} m_in_0} - \frac{| a_0 | ^2\alpha \omega _0 \epsilon a_1}{V_g^2 - C_s^2} \frac{1}{8{\rm \pi} m_in_0} - \frac{\epsilon a_1 \alpha\omega _0 | a_0 | ^2}{V_g^2 - C_s^2} \frac{1}{8{\rm \pi} m_in_0}=0, \end{align}

(3.22)\begin{equation} \frac{\partial a_1 }{\partial \tau} + \frac{a_0V_g' }{2} \frac{\partial ^2 \theta _1 }{\partial \xi ^2} + \frac{a_0 T }{2} \frac{\partial ^2 \theta _1 }{\partial x^2} + \frac{a_0T }{2} \frac{\partial ^2 \theta _1 }{\partial y^2} = 0, \end{equation}

(3.23)\begin{align} & d_0\frac{\partial ^2d_1^ * }{\partial \xi ^2} + d_0^ * \frac{\partial ^2d_1 }{\partial \xi ^2} - {\nu ^2}d_0 \frac{\partial ^2d_1^ * }{\partial x^2} - {\nu ^2}d_0^ * \frac{\partial ^2d_1 }{\partial x^2}- {\nu ^2}d_0 \frac{\partial ^2d_1^* }{\partial y^2} - {\nu ^2}d_0^ * \frac{\partial ^2d_1 }{\partial y^2} \nonumber\\ & \quad - \frac{Qa_0 \epsilon}{8{\rm \pi} m_in_0}\frac{\partial ^2a_1^ *}{\partial x^2} - \frac{Qa_0^ * \epsilon}{8{\rm \pi} m_in_0}\frac{\partial ^2a_1}{\partial x^2} - \frac{Qa_0 \epsilon}{8{\rm \pi} m_in_0}\frac{\partial ^2a_1^ *}{\partial y^2} - \frac{Qa_0^ * \epsilon}{8{\rm \pi} m_in_0}\frac{\partial ^2a_1}{\partial y^2} = 0. \end{align}

We now assume that the perturbations have a sinusoidal waveform with wavenumber $k=(k_x,k_y,k_\xi )$ and frequency ${\omega }$ as follows:

(3.24)\begin{align} a_1 = A{\exp({{\rm i}(k_x x + k_y y + k_\xi \xi - \omega \tau)}} + A^ * {\exp({- {\rm i}( k_xx + k_yy + k_\xi \xi - \omega \tau)})}, \end{align}

(3.25)\begin{align} d_1 = D{\exp({{\rm i}( k_x x + k_y y + k_\xi \xi - \omega \tau)})} + D^ * {\exp({ - {\rm i}( k_xx + k_yy+ k_\xi \xi - \omega \tau)})}, \end{align}

(3.26)\begin{align} \theta_1 = \varTheta{\exp({{\rm i}( k_x x + k_y y + k_\xi \xi - \omega \tau)})} + \varTheta^ * {\exp({ - {\rm i}( k_xx + k_yy + k_\xi \xi - \omega \tau)})}. \end{align}

Substituting these equations into (3.21)–(3.23) we have

(3.27)\begin{align} & \frac{\partial \theta_0 }{\partial \tau}({A{{\rm e}^{{\rm i}\chi }} + A^ * {{\rm e}^{ - {\rm i}\chi }}})+\left({\frac{k_x^2 T }{2} + \frac{k_y^2T }{2}+\frac{k_\xi ^2V_g' }{2}}\right)({A{{\rm e}^{{\rm i}\chi }} + A^ * {{\rm e}^{ - {\rm i}\chi }}}) \nonumber\\ & \quad +\frac{\omega _0 \alpha V_g^2 d_0^2}{V_g^2 - C_s^2}( {C{{\rm e}^{{\rm i}\chi }} + C^ * {{\rm e}^{ - {\rm i}\chi }}})+ \frac{\omega _0 C_s^2 d_0^2 ({1-2\alpha})}{V_g^2 - C_s^2} ({C{{\rm e}^{{\rm i}\chi }} + C^ * {{\rm e}^{ - {\rm i}\chi }}}) \nonumber\\ & \quad + \frac{3 \epsilon \omega _0a_0^2 ({1-\alpha})}{8{\rm \pi} m_in_0 (V_g^2 - C_s^2)} ({C{{\rm e}^{{\rm i}\chi }} + C^ * {{\rm e}^{ - {\rm i}\chi }}}) + \frac{2a_0 \omega _0 C_s^2 d_0({1-2\alpha})}{V_g^2 - C_s^2} ({D{{\rm e}^{{\rm i}\chi }}+ D^ * {{\rm e}^{ - {\rm i}\chi }}}) \nonumber\\ & \quad +\frac{2\alpha \omega _0 a_0 V_g^2d_0}{V_g^2 - C_s^2} ({D{{\rm e}^{{\rm i}\chi }} + D^ * {{\rm e}^{ - {\rm i}\chi }}}) +{\rm i}\omega a_0 ( {\varTheta ^ * {\rm e}^{ - {\rm i}\chi } - \varTheta {{\rm e}^{{\rm i}\chi }}})=0, \end{align}

(3.28)\begin{gather} {\rm i}\omega ( A^ * {{\rm e}^{ - {\rm i}\chi }} - A{{\rm e}^{{\rm i}\chi }}) - \left(\frac{a_0 k_\xi ^2V_g' }{2} + \frac{a_0 k_x^2T }{2} + \frac{a_0 k_y^2T }{2}\right) ({\varTheta {\rm e}^{{\rm i}\chi } + \varTheta ^ * {\rm e}^{ - {\rm i}\chi }}) = 0, \end{gather}

(3.29)\begin{gather}\left({\frac{Q a_0 \epsilon k_x^2 }{8{\rm \pi} m_in_0} + \frac{Qa_0 \epsilon k_y^2 }{8{\rm \pi} m_in_0}}\right)( {{A \,{\rm e}^{{\rm i}\chi }} + A^ * {{\rm e}^{ - {\rm i}\chi }}}) +( {\nu ^2d_0 k_x^2 + \nu ^2 d_0 k_y^2 - d_0k_\xi ^2}) ({{De^{{\rm i}\chi }} + D^ * {{\rm e}^{ - {\rm i}\chi }}}) = 0, \end{gather}

where ${\chi = k_x x + k_y y + k_\xi \xi - \omega \tau }$.

We have the following equations from the coefficient of the term of ${{\rm e}^{{\rm i}\chi }}$:

(3.30)\begin{align} & \left(\frac{k_x^2T }{2} + \frac{k_y^2T }{2} +\frac{k_\xi ^2V_g' }{2} +\frac{2 \epsilon \omega _0a_0^2 ({1-\alpha}) }{8{\rm \pi} m_in_0 (V_g^2 - C_s^2)}\right)A \nonumber\\ & \quad +\left[\frac{{2 a_0 \omega_0 \alpha V_g^2 d_0}}{V_g^2 - C_s^2}+{{2 a_0 \omega _0 C_s^2 d_0 (1-2 \alpha)} \over V_g^2 - C_s^2}\right]D - {{\rm i}\omega a_0} \varTheta = 0, \end{align}

(3.31)\begin{gather} {{\rm i}\omega A }+ \left(\frac{a_0 k_x^2T }{2} + \frac{a_0 k_y^2T }{2} +\frac{a_0 k_\xi ^2V_g'}{2}\right)\varTheta= 0, \end{gather}

(3.32)\begin{gather}\frac{Q a_0 \epsilon ({k_x^2 +k_y^2})}{8{\rm \pi} m_in_0}A + ({\nu ^2 d_0k_x^2} + {\nu ^2 d_0k_y^2} -{d_0k_\xi ^2})D = 0. \end{gather}

In order to obtain the non-trivial solution from (3.30)–(3.32), we have the following equation:

(3.33)\begin{align} {\omega ^2} & = \left[\frac{1 }{4}{(k_x^2 T +k_y^2 T + k_\xi^2 V_g')} +\frac{\epsilon \omega _0a_0^2 ({1-\alpha}) }{8{\rm \pi} m_in_0 (V_g^2 - C_s^2)} \right. \nonumber\\ & \quad \left.-\frac{\omega _0a_0^2 Q \epsilon (\alpha V_g^2 +C_s^2 -2 \alpha C_s^2)}{8{\rm \pi} m_in_0 (V_g^2 - C_s^2)} \frac{{k_x^2 +k_y^2}}{{k_\xi-\nu^2 k_x^2 - \nu^2 k_y^2}}\right] {(k_x^2 T + k_y^2 T + k_\xi V_g')}, \end{align}

where $\omega _0 = c^2k_0^2 \omega _{{\rm ce}} / ({\omega _{{\rm pe}}^2 + c^2 k_0^2})$, $\epsilon = \omega _{{\rm pe}}^2 / \omega _0({\omega _{{\rm ce}} - \omega _0})$, $k_0= \lambda _e^{-1} \alpha ^{1/2}(1-\alpha )^{-1/2}$, $V_g = 2(1-\alpha ) \omega _0 / k_0$, $V_g' = 2( {1 - \alpha } ) ( {1 - 4\alpha } ){\omega _0} / {k_0^2}$, $T={{(1-2\alpha ){\omega _0}} / {k_0^2}}$, $\lambda _e = c / \omega _{{\rm pe}}$, $\alpha = {\omega _0 / \omega _{{\rm ce}} }$, $\omega _{{\rm pe}} = {(4{\rm \pi} n_ee^2 / m_e)}^{1/2}$, $\omega _{{\rm ce}} = eB_0/m_e$, $C_s = {(\gamma kT_i /m_i )}^{1/2}$, $C_A = {B_0 / (4{\rm \pi} m_i n_e)^{1/2}}$, $\nu ^2 = [C_s^2V_g^2 / (V_g^2 - C_s^2) + C_A^2] / (V_g^2 - C_A^2)$, $Q=[C_s^2 / (V_g^2 - C_s^2) + \alpha / (1-\alpha )] / (V_g^2 - C_A^2)$.

Equation (3.33) is the dispersion relation of the perturbed wave.

4. Discussion for some special cases

To study the dispersion relation of the perturbed wave of (3.33), we consider three typical cases.

First, $(k_x, k_y, k_\xi )=(0, 0, k_\xi )$, in which the wave propagates in the direction of $\xi =z-V_gt$, i.e. in the $z$ direction. In other words, the perturbed wave propagates in the direction of the external magnetic field. For this case, (3.33) becomes

(4.1)\begin{equation} {\omega ^2} = \left[\frac{1 }{4}k_\xi^2 V_g' +\frac{\epsilon \omega _0a_0^2 ({1-\alpha}) }{8{\rm \pi} m_in_0 (V_g^2 - C_s^2)}\right]k_\xi^2 V_g'. \end{equation}

In the following, we study the frequency of the perturbed wave from (4.1) by using the plasma parameters (Kostrov et al. 2003) $B_0 = 6.5\times 10^{-3}$ T, $n_0 = 1.2\times 10^{18}$ m$^{-3}$, $\omega _{{\rm pe}} = 6.7\times 10^{10}$ s$^{-1}$, $\omega _{{\rm ce}} = 1.76\times 10^9$ s$^{-1}$, $T_e = 1.16\times 10^5$ K, $T_i = 5.8\times 10^3$ K, $C_s = 5.25\times 10^3$ m s$^{-1}$, $C_A = 2.9\times 10^4$ m s$^{-1}$, $m_i / m_e = 73\,400$, $m_e = 9.11\times 10^{-31}$ kg, $a_0 = 1$.

Figure 1 shows the dependence of $\omega ^2$ on parameters of both $k$ and $\alpha$. It is observed that the frequency approaches zero as both $k$ and $\alpha$ tend to zero. The frequency increases as $k$ increases. Furthermore, it is zero when $k<1.78$. However, the frequency decreases as $\alpha$ increases.

Figure 1. Dependence of $\omega ^2$ on both perturbed wavenumber $k$ and $\alpha$ with $B_0 = 6.5\times 10^{-3}$ T, $n_0 = 1.2\times 10^{18}$ m$^{-3}$, $\omega _{{\rm pe}} = 6.7\times 10^{10}$ s$^{-1}$, $\omega _{{\rm ce}} = 1.76\times 10^{9}$ s$^{-1}$, $T_e = 1.16\times 10^5$ K, $T_i = 5.8\times 10^3$ K, $C_s = 5.25\times 10^3$ m s$^{-1}$, $C_A = 2.9\times 10^4$ m s$^{-1}$, $m_i / m_e = 73\,400$, $m_e = 9.11\times 10^{31}$ kg, $a_0 = 1$.

In order to further understand the variation of the frequency with respect to both $k$ and $\alpha$, figure 2 shows the dependence of $\alpha$ on $k$ when $\omega$ remains a constant.

Figure 2. Dependence of $\alpha$ on $k$ where $\omega ^2 = 7.4\,{\rm s}^{-2}$ and $\omega ^2 = 1.5\,{\rm s}^{-2}$ in two curves, respectively, the other parameters are $B_0 = 6.5\times 10^{-3}$ T, $n_0 =1.2\times 10^{18}$ m$^{-1}$, $\omega _{{\rm pe}} = 6.7\times 10^{10}$ s$^{-1}$, $\omega _{{\rm ce}} = 1.76\times 10^9$ s$^{-1}$, $T_e = 1.16\times 10^5$ K, $T_i = 5.8\times 10^3$ K, $C_s = 5.25\times 10^3$ m s$^{-1}$, $C_A = 2.9\times 10^4$ m s$^{-1}$, $m_i / m_e = 73\,400$, $m_e = 9.11\times 10^{-31}$ k, $a_0 = 1$.

The fitted equations of two curves in figure 2 are as follows:

(4.2)\begin{equation} \left.\begin{gathered} {\alpha_1} = ({-}0.92)\exp({-}k_1 / 1.22) +0.21,\\ {\alpha_2} = ({-}0.97)\exp({-}k_2 / 1.31) +0.20. \end{gathered}\right\} \end{equation}

Second, $(k_x, k_y, k_\xi )=(k_x, 0, 0)$, about which the propagation direction of the perturbed wave is perpendicular to that of the external magnetic field. Then (3.33) becomes

(4.3)\begin{align} {\omega ^2} & = \left[\frac{1 }{4}k_x^2 T +\frac{\epsilon \omega _0a_0^2 ({1-\alpha}) }{8{\rm \pi} m_in_0 (V_g^2 - C_s^2)} \right. \nonumber\\ & \quad \left.+\frac{\omega _0a_0^2 Q \epsilon (\alpha V_g^2 +C_s^2 -2 \alpha C_s^2)}{8{\rm \pi} m_in_0 (V_g^2 - C_s^2)}\right]k_x^2 T. \end{align}

We also use the same system parameters (Kostrov et al. 2003): $B_0 = 6.5\times 10^{-3}$ T, $n_0 = 1.2\times 10^{18}$ m$^{-3}$, $\omega _{\textrm {pe}} = 6.7\times 10^{10}$ s$^{-1}$, $\omega _{\textrm {ce}} = 1.76\times 10^9$ s$^{-1}$, $T_e = 1.16\times 10^5$ K, $T_i = 5.8\times 10^3$ K, $C_s = 5.25\times 10^3$ m s$^{-1}$, $C_A = 2.9\times 10^4$ m s$^{-1}$, $m_i / m_e = 73\,400$, $m_e = 9.11\times 10^{-31}$ kg, $a_0 = 1$.

Figure 3 shows the dependence of $\omega ^2$ on parameters of both $k$ and $\alpha$. It is observed that the frequency approaches zero as both $k$ and $\alpha$ tend to zero. The frequency increases as $k$ increases. Furthermore, it is zero when $k<1.78$. However, the frequency decreases as $\alpha$ increases.

Figure 3. Dependence of $\omega ^2$ on both perturbed wavenumber $k$ and $\alpha$ with $B_0 = 6.5\times 10^{-3}$ T, $n_0 = 1.2\times 10^{18}$ m$^{-3}$, $\omega _{\textrm {pe}} = 6.7\times 10^{10}$ s$^{-1}$, $\omega _{\textrm {ce}} = 1.76\times 10^{9}$ s$^{-1}$, $T_e = 1.16\times 10^{5}$ K, $T_i = 5.8\times 10^3$ K, $C_s = 5.25\times 10^{3}$ m s$^{-1}$, $C_A = 2.9\times 10^{4}$ m s$^{-1}$, $m_i / m_e = 73\,400$, $m_e = 9.11\times 10^{-31}$ kg, $a_0 = 1$.

In order to further understand the variation of the frequency with respect to both $k$ and $\alpha$, figure 4 shows the dependence of $\alpha$ on $k$ when $\omega$ remains a constant.

Figure 4. Dependence of $\alpha$ on $k$ where $\omega ^2 = 3.7\,\textrm {s}^{-2}$ and $\omega ^2 = 5.6\,\textrm {s}^{-2}$ in two curves, respectively, the other parameters are $B_0 = 6.5\times 10^{-3}$ T, $n_0 = 1.2\times 10^{18}$ m$^{-3}$, $\omega _{\textrm {pe}} = 6.7\times 10^{10}$ s$^{-1}$, $\omega _{\textrm {ce}} = 1.76\times 10^{9}$ s$^{-1}$, $T_e = 1.16\times 10^{5}$ K, $T_i = 5.8\times 10^{3}$ K, $C_s = 5.25\times 10^{3}$ m s$^{-1}$, $C_A = 2.9\times 10^{4}$ m s$^{-1}$, $m_i / m_e = 73\,400$, $m_e = 9.11\times 10^{-31}$ kg, $a_0 = 1$.

The fitted equations of two curves in figure 4 are as follows:

(4.4)\begin{equation} \left.\begin{gathered} {\alpha_1} = ({-}2.04)\exp({-}k_1 / 1.28) +0.40,\\ {\alpha_2} = ({-}2.04)\exp({-}k_2 / 1.34) +0.39. \end{gathered}\right\} \end{equation}

Third, $(k_x, k_y, k_\xi )= (k, 0, \sigma k)$, where $\sigma =\tan \theta _{xz}$, and $\theta _{xz}$ is the angle between the direction of the external magnetic field and the vector of the wavenumber. It stands for the case in which the perturbed waves propagates in an arbitrary direction, i.e. $0\leq \theta \leq {{\rm \pi} }/{2}$. For this case, (3.33) becomes

(4.5)\begin{align} {\omega ^2} & = \left[\frac{1}{4}{(\sigma^2 k^2 V_g' + k^2 T)} +\frac{\epsilon \omega _0a_0^2 ({1-\alpha}) }{8{\rm \pi} m_in_0 (V_g^2 - C_s^2)} \right.\nonumber\\ & \quad \left. -\frac{\omega _0a_0^2 Q \epsilon (\alpha V_g^2 +C_s^2 -2 \alpha C_s^2)}{8{\rm \pi} m_in_0 (V_g^2 -C_s^2)(\sigma^2-\nu^2)}\right]{(\sigma^2 k^2 V_g' + k^2 T)}. \end{align}

We also use the same system parameters (Kostrov et al. 2003): $B_0 = 6.5\times 10^{-3}$ T, $n_0 = 1.2\times 10^{18}$ m$^{-3}$, $\omega _{\textrm {pe}} = 6.7\times 10^{10}$ s$^{-1}$, $\omega _{\textrm {ce}} = 1.76\times 10^{9}$ s$^{-1}$, $T_e = 1.16\times 10^{5}$ K, $T_i = 5.8\times 10^{3}$ K, $C_s = 5.25\times 10^{3}$ m s$^{-1}$, $C_A = 2.9\times 10^{4}$ m s$^{-1}$, $m_i / m_e = 73\,400$, $m_e = 9.11\times 10^{-31}$ kg, $a_0 = 1$, $\sigma = 1$.

Figure 5 shows the dependence of $\omega ^2$ on parameters of both $k$ and $\alpha$. It is observed that the frequency approaches zero as both $k$ and $\alpha$ tend to zero. The frequency increases as $k$ increases. Furthermore, it is zero when $k<1.78$. However, the frequency decreases as $\alpha$ increases.

Figure 5. Dependence of $\omega ^2$ on both perturbed wavenumber $k$ and $\alpha$ with $B_0 = 6.5\times 10^{-3}$ T, $n_0 = 1.2\times 10^{18}$ m$^{-3}$, $\omega _{\textrm {pe}} = 6.7\times 10^{10}$ s$^{-1}$, $\omega _{\textrm {ce}} = 1.76\times 10^{9}$ s$^{-1}$, $T_e = 1.16\times 10^{5}$ K, $T_i = 5.8\times 10^{3}$ K, $C_s = 5.25\times 10^{3}$ m s$^{-1}$, $C_A = 2.9\times 10^{4}$ m s$^{-1}$, $m_i / m_e = 73\,400$, $m_e = 9.11\times 10^{-31}$ kg, $a_0 = 1$, $\sigma = 1$.

In order to further understand the variation of the frequency with respect to both $k$ and $\alpha$, figure 6 shows the dependence of $\alpha$ on $k$ when $\omega$ remains a constant.

Figure 6. Dependence of $\alpha$ on $k$ where $\omega ^2 = 3.3\,\textrm {s}^{-2}$ and $\omega ^2 = 5.0\,\textrm {s}^{-2}$ in two curves, respectively, the other parameters are $B_0 = 6.5\times 10^{-3}$ T, $n_0 =1.2\times 10^{18}$ m$^{-3}$, $\omega _{\textrm {pe}} = 6.7\times 10^{10}$ s$^{-1}$, $\omega _{\textrm {ce}} = 1.76\times 10^{9}$ s$^{-1}$, $T_e = 1.16\times 10^{5}$ K, $T_i = 5.8\times 10^{3}$ K, $C_s = 5.25\times 10^{3}$ m s$^{-1}$, $C_A = 2.9\times 10^{4}$ m s$^{-1}$, $m_i / m_e = 73\,400$, $m_e = 9.11\times 10^{-31}$ kg, $a_0 = 1$, $\sigma = 1$.

The fitted equations of two curves in figure 6 are as follows:

(4.6)\begin{equation} \left.\begin{gathered} {\alpha_1} = ({-}1.23)\exp({-}k_1 / 1.38) +0.24,\\ {\alpha_2} = ({-}1.23)\exp({-}k_2 / 1.44) +0.24. \end{gathered}\right\} \end{equation}

5. Instability conditions of the perturbed wave

The above study shows that $\omega ^2>0$, which indicates that there is no instability. However, for different parameters, instability may exist. Figure 7 shows the dependence of $\omega ^2$ on the parameters of both $\sigma$ and $k_0$, where $\alpha <1$ since $\omega _0 < \omega _{\textrm {ce}}$ and $\alpha = \omega _0 / \omega _{\textrm {ce}}$. It is shown in figure 7 that $\omega ^2 < 0$ for both the first case and the second case in certain regions, where $k=0.001$. It seems from figure 7 that $\omega ^2$ may be negative in some regions when $k_0 < 0.05$. Furthermore, $\omega ^2$ decreases as the $\sigma$ increases. However, $\omega ^2$ increases as the whistler wavenumber $k_0$ increases. It suggests that there is instability when the whistler wave propagates perpendicular to or parallel to the direction of the external magnetic field. However, it is found that $\omega ^2 >0$ is always satisfied for the third case, which means that it is stable if the angle between the external magnetic field and the perturbed wave's direction is ${{\rm \pi} }/{4}$ ($\sigma =1$).

Figure 7. Dependence of $\omega ^2$ on the wave propagation direction $\sigma$ and the whistle wave number $k_0$ where $k=0.001$, $B_0 = 6.5\times 10^{-3}$ T, $n_0 = 1.2\times 10^{18}$ m$^{-3}$, $\omega _{\textrm {pe}} = 6.7\times 10^{10}$ s$^{-1}$, $\omega _{\textrm {ce}} = 1.76\times 10^{9}$ s$^{-1}$, $T_e = 1.16\times 10^{5}$ K, $T_i = 5.8\times 10^{3}$ K, $C_s = 5.25\times 10^{3}$ m s$^{-1}$, $C_A = 2.9\times 10^4$ m s$^{-1}$, $m_i / m_e = 73\,400$, $m_e = 9.11\times 10^{-31}$ kg, $a_0 = 1$, $k_b = 1.38\times 10^{-23}$ J K$^{-1}$, $\epsilon _0 = 8.85\times 10^{-12}$ F m$^{-1}$, $\mu _0 = 1.26\times 10^{-6}$ H m$^{-1}$.

Figure 8 shows $\omega ^2$ is positive when $k_0 > 0.05$. Here $\omega ^2$ increases as the $\sigma$ increases when $\sigma > 25$. Whereas, $\omega ^2$ first increases as $k_0$ increases, reaches a peak value, and then decreases as $k_0$ increases.

Figure 8. Dependence of $\omega ^2$ on $k_0$ where $k = 0.001$, $\sigma = 180$, $k=0.001$, $B_0 = 6.5\times 10^{-3}$ T, $n_0 = 1.2\times 10^{18}$ m$^{-3}$, $\omega _{\textrm {pe}} = 6.7\times 10^{10}$ s$^{-1}$, $\omega _{\textrm {ce}} = 1.76\times 10^{9}$ s$^{-1}$, $T_e = 1.16\times 10^{5}$ K, $T_i = 5.8\times 10^{3}$ K, $C_s = 5.25\times 10^{3}$ m s$^{-1}$, $C_A = 2.9\times 10^{4}$ m s$^{-1}$, $m_i / m_e = 73\,400$, $m_e = 9.11\times 10^{-31}$ kg, $a_0 = 1$, $k_b = 1.38\times 10^{-23}$ J K$^{-1}$, $\epsilon _0 = 8.85\times 10^{-12}$ F m$^{-1}$, $\mu _0 = 1.26\times 10^{-6}$ H m$^{-1}$.

6. Conclusion

The present investigation focuses on the modulational instability of the nonlinearly interacting electron whistlers and magnetosonic perturbations. It is found that the wave is modulational stable for typical plasma parameters. However, modulational instability appears in special cases. The results show that modulational instability appears in some regions when the whistler wavenumber satisfies $k_0 < 0.05$. Moreover, the growth rate decreases as the angle between the external magnetic field and the perturbed wave's direction increases. However, the growth rate increases as the whistler wavenumber $k_0$ increases.

It is also found that there is no modulational instability when the whistler wavenumber satisfies $k_0 > 0.05$. In this case, the perturbed wave frequency increases as the angle between the external magnetic field and the perturbed wave's direction increases when the angle between the external magnetic field and the perturbed wave's direction is large enough. Whereas, the perturbed wave frequency first increases as the whistler wavenumber increases, reaches a peak value and then decreases as whistler wavenumber increases.