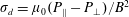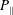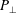1 Introduction
For favourable confinement, it is desirable that the equilibrium states of fusion plasmas are stable and therefore their stability study is of great importance. Such low entropy states are susceptible to numerous instabilities such as strong ideal pressure and current driven modes, resistive instabilities often associated with magnetic reconnection, and kinetic micro-instabilities which occur when the distribution functions depart from Maxwellians. Also, certain instabilities are a source of turbulence, which can drive transport. Investigation of macro-instabilities is usually performed within the framework of ideal magnetohydrodynamics (MHD), since this model is a good approximation in describing the plasma as a macroscopic fluid and capturing most of the physics of the force balance.
There are two main methods for studying MHD stability: first, for small perturbations from the equilibrium, linear stability is examined by the normal mode analysis which can calculate the perturbation growth rate and, second, the use of variational principles, involving perturbations of arbitrary amplitude and therefore covering the nonlinear regime, in connection with the sign of the perturbation potential energy. For static equilibria Bernstein et al. (Reference Bernstein, Frieman, Kruskal and Kulsrud1958) have derived a well-known energy principle which provides necessary and sufficient conditions for linear stability.
It is also known that plasma flows in magnetic confinement devices, either induced by external heating sources, such as electromagnetic waves and neutral beams, or developed intrinsically, play an important role in the formation of transport barriers and the transitions to improved confinement regimes, such as the low-to-high confinement (L-H) transition. In the presence of flow, however, the problem of stability becomes much tougher because of the anti-Hermitian convective flow term in the momentum equation. As a result, only sufficient conditions for the linear stability of stationary equilibria were previously obtained; see Frieman & Rotenberg (Reference Frieman and Rotenberg1960), Hameiri (Reference Hameiri1998), Vladimirov & Ilin (Reference Vladimirov and Ilin1998), Ilin & Vladimirov (Reference Ilin and Vladimirov2004) and Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007). Particularly, in connection with the present study, the derivation of a sufficient condition for the linear stability of ideal MHD equilibria and plasmas of constant density, isotropic pressure and incompressible flow parallel to the magnetic field, was initiated in Vladimirov & Ilin (Reference Vladimirov and Ilin1998) and Ilin & Vladimirov (Reference Ilin and Vladimirov2004) and completed in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007). A key element to obtain this condition is that the pressure perturbation remains arbitrary, that is, there is no need to express the perturbation in terms of the Lagrangian displacement vector.
Also, in high temperature plasmas, the collision time is so long that collisions can be neglected. Owing to the low collision frequency, a high temperature plasma remains anisotropic for a long time, once anisotropy is induced, e.g. by external heating sources. Macroscopic equations for a collisionless plasma with pressure anisotropy have been derived in Chew, Goldberger & Low (Reference Chew, Goldberger and Low1956). A detailed review of the anisotropic Chew–Goldberger-Low (CGL) model as well as of other collisionless fluid models is provided in Hunana et al. (Reference Hunana, Tenerani, Zank, Khomenko, Goldstein, Webb, Cally, Collados, Velli and Adhikari2019). Pressure anisotropy is usually responsible for various instabilities, such as the firehose and the mirror instabilities. Therefore, investigation of the stability properties of anisotropic plasmas, either static or stationary, is also a significant objective.
In the present work we derive a sufficient condition for the linear stability of equilibria with field-aligned incompressible flows associated with plasmas of constant density and constant anisotropy function,
![]() $\unicode[STIX]{x1D70E}_{d}$
, working along the same lines as in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007). Then, we examine the stability properties of such anisotropic equilibria. Specifically, in § 2 we present the basic dynamical MHD equations with anisotropic pressure and their equilibrium counterparts, while in § 3 we linearise the time dependent equations for small perturbations around the equilibrium quantities, and obtain a pertinent functional of the perturbation potential energy. In § 4 the sufficient condition is obtained in the presence of pressure anisotropy, which generalises the one of Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007) being valid for isotropic pressure. To derive that condition it is also important that the perturbation of the effective pressure,
$\unicode[STIX]{x1D70E}_{d}$
, working along the same lines as in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007). Then, we examine the stability properties of such anisotropic equilibria. Specifically, in § 2 we present the basic dynamical MHD equations with anisotropic pressure and their equilibrium counterparts, while in § 3 we linearise the time dependent equations for small perturbations around the equilibrium quantities, and obtain a pertinent functional of the perturbation potential energy. In § 4 the sufficient condition is obtained in the presence of pressure anisotropy, which generalises the one of Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007) being valid for isotropic pressure. To derive that condition it is also important that the perturbation of the effective pressure,
![]() ${\mathcal{P}}=(P_{\Vert }+P_{\bot })/2$
, remains arbitrary. Furthermore, in § 5 we show that, whenever a given equilibrium is linearly stable, then all families of equilibria derived by the symmetry transformations introduced in Bogoyavlenskij (Reference Bogoyavlenskij2001) and Evangelias & Throumoulopoulos (Reference Evangelias and Throumoulopoulos2019), are also linearly stable provided that a parameter involved in those transformations is positive. In addition, in § 6 we apply the derived sufficient condition to a class of analytic helically symmetric equilibria in order to examine the impact of pressure anisotropy, flow, and certain geometrical parameters characterising helical configurations, such as the torsion and pitch length, on the stability of those equilibria. Finally, § 7 summarises the main results.
${\mathcal{P}}=(P_{\Vert }+P_{\bot })/2$
, remains arbitrary. Furthermore, in § 5 we show that, whenever a given equilibrium is linearly stable, then all families of equilibria derived by the symmetry transformations introduced in Bogoyavlenskij (Reference Bogoyavlenskij2001) and Evangelias & Throumoulopoulos (Reference Evangelias and Throumoulopoulos2019), are also linearly stable provided that a parameter involved in those transformations is positive. In addition, in § 6 we apply the derived sufficient condition to a class of analytic helically symmetric equilibria in order to examine the impact of pressure anisotropy, flow, and certain geometrical parameters characterising helical configurations, such as the torsion and pitch length, on the stability of those equilibria. Finally, § 7 summarises the main results.
2 Basic equations and background equilibria
The dynamics of a perfectly conducting plasma with anisotropic pressure is determined by the following set of equations:
Here,
![]() $\boldsymbol{B}^{\ast }(\boldsymbol{r},t)$
is the magnetic field,
$\boldsymbol{B}^{\ast }(\boldsymbol{r},t)$
is the magnetic field,
![]() $\boldsymbol{J}^{\ast }(\boldsymbol{r},t)$
the current density,
$\boldsymbol{J}^{\ast }(\boldsymbol{r},t)$
the current density,
![]() $\unicode[STIX]{x1D707}_{0}$
the magnetic constant,
$\unicode[STIX]{x1D707}_{0}$
the magnetic constant,
![]() $\boldsymbol{V}^{\ast }(\boldsymbol{r},t)$
the plasma velocity,
$\boldsymbol{V}^{\ast }(\boldsymbol{r},t)$
the plasma velocity,
![]() $\unicode[STIX]{x1D71A}^{\ast }(\boldsymbol{r},t)$
the mass density and
$\unicode[STIX]{x1D71A}^{\ast }(\boldsymbol{r},t)$
the mass density and
![]() $\unicode[STIX]{x1D64B}^{\ast }$
the pressure tensor defined as
$\unicode[STIX]{x1D64B}^{\ast }$
the pressure tensor defined as
where
![]() $\unicode[STIX]{x1D644}$
is the unit tensor;
$\unicode[STIX]{x1D644}$
is the unit tensor;
![]() $\unicode[STIX]{x2202}_{t}$
denotes the time derivative, while the Lagrangian derivative is defined as
$\unicode[STIX]{x2202}_{t}$
denotes the time derivative, while the Lagrangian derivative is defined as
![]() $D_{t}\equiv \unicode[STIX]{x2202}_{t}+(\boldsymbol{V}^{\ast }\boldsymbol{\cdot }\unicode[STIX]{x1D735})$
. The pressure tensor is diagonal in a local rectangular system with respect to
$D_{t}\equiv \unicode[STIX]{x2202}_{t}+(\boldsymbol{V}^{\ast }\boldsymbol{\cdot }\unicode[STIX]{x1D735})$
. The pressure tensor is diagonal in a local rectangular system with respect to
![]() $\boldsymbol{B}^{\ast }$
, and consists of the scalar pressure elements
$\boldsymbol{B}^{\ast }$
, and consists of the scalar pressure elements
![]() $P_{\Vert }^{\ast }(\boldsymbol{r},t)$
and
$P_{\Vert }^{\ast }(\boldsymbol{r},t)$
and
![]() $P_{\bot }^{\ast }(\boldsymbol{r},t)$
along and across
$P_{\bot }^{\ast }(\boldsymbol{r},t)$
along and across
![]() $\boldsymbol{B}^{\ast }(\boldsymbol{r},t)$
, respectively, while the dimensionless function
$\boldsymbol{B}^{\ast }(\boldsymbol{r},t)$
, respectively, while the dimensionless function
is a measure of the pressure anisotropy. Particle collisions equilibrating parallel and perpendicular energies lower the value of
![]() $\unicode[STIX]{x1D70E}_{d}^{\ast }$
and, therefore a highly collisional plasma is described accurately by a single scalar pressure,
$\unicode[STIX]{x1D70E}_{d}^{\ast }$
and, therefore a highly collisional plasma is described accurately by a single scalar pressure,
![]() $P_{\text{isotropic}}^{\ast }$
. In view of this fact, when pressure anisotropy is present it is useful to introduce an effective isotropic pressure,
$P_{\text{isotropic}}^{\ast }$
. In view of this fact, when pressure anisotropy is present it is useful to introduce an effective isotropic pressure,
that reduces to
![]() $P_{\text{isotropic}}^{\ast }$
in the absence of anisotropy. By substituting (2.3) and (2.4) into the momentum equation of set (2.1) we obtain
$P_{\text{isotropic}}^{\ast }$
in the absence of anisotropy. By substituting (2.3) and (2.4) into the momentum equation of set (2.1) we obtain
in which the scalar pressures
![]() $P_{\Vert }^{\ast }$
and
$P_{\Vert }^{\ast }$
and
![]() $P_{\bot }^{\ast }$
do not appear explicitly. This is very useful for the stability analysis to follow in the next sections.
$P_{\bot }^{\ast }$
do not appear explicitly. This is very useful for the stability analysis to follow in the next sections.
The counterparts to set (2.1) equilibrium equations are
where the absence of the superscript
![]() $\ast$
denotes equilibrium and therefore no dependence on time.
$\ast$
denotes equilibrium and therefore no dependence on time.
In the special case of collinear velocity and magnetic fields related through
with
![]() $\unicode[STIX]{x1D706}$
an arbitrary dimensionless scalar function, the continuity equation of the set (2.6) takes the form
$\unicode[STIX]{x1D706}$
an arbitrary dimensionless scalar function, the continuity equation of the set (2.6) takes the form
![]() $(\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D71A})/\unicode[STIX]{x1D71A}=-2(\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D706})/\unicode[STIX]{x1D706}$
; substitution of the latter relation in the counterpart to (2.5), the equilibrium momentum equation, yields
$(\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D71A})/\unicode[STIX]{x1D71A}=-2(\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D706})/\unicode[STIX]{x1D706}$
; substitution of the latter relation in the counterpart to (2.5), the equilibrium momentum equation, yields
 $$\begin{eqnarray}\displaystyle (1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})\boldsymbol{J}\times \boldsymbol{B} & = & \displaystyle \unicode[STIX]{x1D735}\left({\mathcal{P}}+\unicode[STIX]{x1D706}^{2}\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}\unicode[STIX]{x1D735}(1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})-\frac{\boldsymbol{B}}{\unicode[STIX]{x1D707}_{0}}[\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})\boldsymbol{J}\times \boldsymbol{B} & = & \displaystyle \unicode[STIX]{x1D735}\left({\mathcal{P}}+\unicode[STIX]{x1D706}^{2}\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}\unicode[STIX]{x1D735}(1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})-\frac{\boldsymbol{B}}{\unicode[STIX]{x1D707}_{0}}[\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})].\end{eqnarray}$$
Equation (2.8) is valid for arbitrary functions
![]() $\unicode[STIX]{x1D71A}$
and
$\unicode[STIX]{x1D71A}$
and
![]() $\unicode[STIX]{x1D70E}_{d}$
, and therefore for compressible flows.
$\unicode[STIX]{x1D70E}_{d}$
, and therefore for compressible flows.
Furthermore, we assume that the mass density and the anisotropy function remain constant everywhere inside a volume
![]() ${\mathcal{D}}$
:
${\mathcal{D}}$
:
![]() $\unicode[STIX]{x1D71A},\unicode[STIX]{x1D70E}_{d}=\text{const.}$
Consequently, the corresponding field-aligned equilibrium flow becomes incompressible and the function
$\unicode[STIX]{x1D71A},\unicode[STIX]{x1D70E}_{d}=\text{const.}$
Consequently, the corresponding field-aligned equilibrium flow becomes incompressible and the function
![]() $\unicode[STIX]{x1D706}$
is constant on magnetic surfaces
$\unicode[STIX]{x1D706}$
is constant on magnetic surfaces
![]() $\unicode[STIX]{x1D713}=\text{const.}$
, whenever such surfaces exist. Also, both the magnetic and velocity fields lie on those surfaces,
$\unicode[STIX]{x1D713}=\text{const.}$
, whenever such surfaces exist. Also, both the magnetic and velocity fields lie on those surfaces,
![]() $\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D713})=\boldsymbol{V}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D713})=0$
. It is known that the existence of three-dimensional equilibria with nested toroidal magnetic surfaces is not guaranteed and, in general, irrespective of the existence of magnetic surfaces, the function
$\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D713})=\boldsymbol{V}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D713})=0$
. It is known that the existence of three-dimensional equilibria with nested toroidal magnetic surfaces is not guaranteed and, in general, irrespective of the existence of magnetic surfaces, the function
![]() $\unicode[STIX]{x1D706}$
is constant on both the magnetic field lines and the velocity streamlines. Henceforth, we will presume the existence of well-defined equilibrium magnetic surfaces. Under these assumptions, equation (2.8) takes the simpler form
$\unicode[STIX]{x1D706}$
is constant on both the magnetic field lines and the velocity streamlines. Henceforth, we will presume the existence of well-defined equilibrium magnetic surfaces. Under these assumptions, equation (2.8) takes the simpler form
where the prime denotes differentiation with respect to
![]() $\unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D713}$
and
![]() ${\mathcal{P}}_{s}$
is the total effective pressure in the absence of flow
${\mathcal{P}}_{s}$
is the total effective pressure in the absence of flow
![]() $(\unicode[STIX]{x1D706}=0)$
, defined as
$(\unicode[STIX]{x1D706}=0)$
, defined as
Moreover, projection of (2.9) along
![]() $\boldsymbol{B}$
implies that the static total effective pressure is a surface quantity,
$\boldsymbol{B}$
implies that the static total effective pressure is a surface quantity,
![]() ${\mathcal{P}}_{s}={\mathcal{P}}_{s}(\unicode[STIX]{x1D713})$
, and therefore, the momentum equation (2.9) can be cast into the useful form
${\mathcal{P}}_{s}={\mathcal{P}}_{s}(\unicode[STIX]{x1D713})$
, and therefore, the momentum equation (2.9) can be cast into the useful form
where
Equation (2.11) implies that, for equilibria with field-aligned incompressible flows, constant density and constant anisotropy function, the current surfaces coincide with the magnetic surfaces, that is, the vectors
![]() $\boldsymbol{J}$
,
$\boldsymbol{J}$
,
![]() $\boldsymbol{B}$
lie on common surfaces
$\boldsymbol{B}$
lie on common surfaces
![]() $\unicode[STIX]{x1D713}=\text{const.}$
In the subsequent sections we examine the stability of the aforementioned equilibria to small three-dimensional perturbations. To this end, we define the following quantities:
$\unicode[STIX]{x1D713}=\text{const.}$
In the subsequent sections we examine the stability of the aforementioned equilibria to small three-dimensional perturbations. To this end, we define the following quantities:
from which it follows that
3 Energy principle and perturbation potential energy
In order to examine the linear stability of a given equilibrium with anisotropic pressure and incompressible flow,
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{V}=0$
, we assume that the equilibrium position,
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{V}=0$
, we assume that the equilibrium position,
![]() $\boldsymbol{r}$
, is perturbed to a position
$\boldsymbol{r}$
, is perturbed to a position
![]() $\boldsymbol{r}^{\ast }(\boldsymbol{r},t)$
, through the usual Lagrangian displacement vector
$\boldsymbol{r}^{\ast }(\boldsymbol{r},t)$
, through the usual Lagrangian displacement vector
![]() $\unicode[STIX]{x1D743}(\boldsymbol{r},t)\equiv \boldsymbol{r}^{\ast }-\boldsymbol{r}$
, so that
$\unicode[STIX]{x1D743}(\boldsymbol{r},t)\equiv \boldsymbol{r}^{\ast }-\boldsymbol{r}$
, so that
Here,
![]() $\boldsymbol{b},\boldsymbol{j},p,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D716}$
and
$\boldsymbol{b},\boldsymbol{j},p,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D716}$
and
correspond to small perturbations of the respective equilibrium quantities. Note that we have assumed perturbations of the effective pressure,
![]() ${\mathcal{P}}$
, and the anisotropy function,
${\mathcal{P}}$
, and the anisotropy function,
![]() $\unicode[STIX]{x1D70E}_{d}$
, instead of explicit perturbations of the scalar pressures
$\unicode[STIX]{x1D70E}_{d}$
, instead of explicit perturbations of the scalar pressures
![]() $P_{\Vert }$
and
$P_{\Vert }$
and
![]() $P_{\bot }$
. Also, on the fixed boundary
$P_{\bot }$
. Also, on the fixed boundary
![]() $\unicode[STIX]{x2202}{\mathcal{D}}$
surrounding a plasma domain
$\unicode[STIX]{x2202}{\mathcal{D}}$
surrounding a plasma domain
![]() ${\mathcal{D}}$
of interest, we adopt the following conditions:
${\mathcal{D}}$
of interest, we adopt the following conditions:
where
![]() $\hat{\boldsymbol{n}}$
is the perpendicular outward unit vector on the boundary. Introducing perturbations (3.1) into the dynamical equations (2.1) and employing the equilibrium equations (2.6), we obtain the following linearised equations:
$\hat{\boldsymbol{n}}$
is the perpendicular outward unit vector on the boundary. Introducing perturbations (3.1) into the dynamical equations (2.1) and employing the equilibrium equations (2.6), we obtain the following linearised equations:
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b}=0,\quad \boldsymbol{j}=\frac{1}{\unicode[STIX]{x1D707}_{0}}\unicode[STIX]{x1D735}\times \boldsymbol{b},\quad \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x2202}t}+\boldsymbol{V}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D71A}\boldsymbol{v})=0,\\ \displaystyle \unicode[STIX]{x1D71A}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D71A}[(\boldsymbol{V}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{v}+(\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{V}]-(1-\unicode[STIX]{x1D70E}_{d})(\boldsymbol{J}\times \boldsymbol{b}+\boldsymbol{j}\times \boldsymbol{B})+\unicode[STIX]{x1D735}p=G(\boldsymbol{r},t),\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b}=0,\quad \boldsymbol{j}=\frac{1}{\unicode[STIX]{x1D707}_{0}}\unicode[STIX]{x1D735}\times \boldsymbol{b},\quad \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x2202}t}+\boldsymbol{V}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D71A}\boldsymbol{v})=0,\\ \displaystyle \unicode[STIX]{x1D71A}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D71A}[(\boldsymbol{V}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{v}+(\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{V}]-(1-\unicode[STIX]{x1D70E}_{d})(\boldsymbol{J}\times \boldsymbol{b}+\boldsymbol{j}\times \boldsymbol{B})+\unicode[STIX]{x1D735}p=G(\boldsymbol{r},t),\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle G & := & \displaystyle -\unicode[STIX]{x1D6FF}(\boldsymbol{V}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{V}-\unicode[STIX]{x1D716}\boldsymbol{J}\times \boldsymbol{B}+\frac{1}{\unicode[STIX]{x1D707}_{0}}\left[\vphantom{\left(\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{b}+\frac{\boldsymbol{b}^{2}}{2}\right)}\frac{\boldsymbol{B}^{2}}{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D716}-(\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D716}+\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D70E}_{d})\boldsymbol{B}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\left(\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{b}+\frac{\boldsymbol{b}^{2}}{2}\right)\unicode[STIX]{x1D735}\unicode[STIX]{x1D70E}_{d}-(\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D716})\boldsymbol{b}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G & := & \displaystyle -\unicode[STIX]{x1D6FF}(\boldsymbol{V}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{V}-\unicode[STIX]{x1D716}\boldsymbol{J}\times \boldsymbol{B}+\frac{1}{\unicode[STIX]{x1D707}_{0}}\left[\vphantom{\left(\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{b}+\frac{\boldsymbol{b}^{2}}{2}\right)}\frac{\boldsymbol{B}^{2}}{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D716}-(\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D716}+\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D70E}_{d})\boldsymbol{B}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\left(\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{b}+\frac{\boldsymbol{b}^{2}}{2}\right)\unicode[STIX]{x1D735}\unicode[STIX]{x1D70E}_{d}-(\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D716})\boldsymbol{b}\right].\end{eqnarray}$$
At this point we note that, in order that the set of dynamical equations (2.1) be closed, one needs, in connection with the pressures
![]() $P_{\Vert }^{\ast }$
and
$P_{\Vert }^{\ast }$
and
![]() $P_{\bot }^{\ast }$
, a couple of energy equations or equations of state, e.g. the double adiabatic equations Chew et al. (Reference Chew, Goldberger and Low1956) associated with the known CGL model. In the present study, one such equation of state corresponds to incompressibility in connection with an evolution with constant mass density,
$P_{\bot }^{\ast }$
, a couple of energy equations or equations of state, e.g. the double adiabatic equations Chew et al. (Reference Chew, Goldberger and Low1956) associated with the known CGL model. In the present study, one such equation of state corresponds to incompressibility in connection with an evolution with constant mass density,
![]() $\unicode[STIX]{x1D71A}^{\ast }=\unicode[STIX]{x1D71A}=\text{const.}$
,
$\unicode[STIX]{x1D71A}^{\ast }=\unicode[STIX]{x1D71A}=\text{const.}$
,
![]() $(\unicode[STIX]{x1D6FF}=0)$
. Also, the fact that the momentum equation can be cast in the form (2.5) involving the pressures
$(\unicode[STIX]{x1D6FF}=0)$
. Also, the fact that the momentum equation can be cast in the form (2.5) involving the pressures
![]() $P_{\Vert }^{\ast }$
and
$P_{\Vert }^{\ast }$
and
![]() $P_{\bot }^{\ast }$
only implicitly through the effective pressure,
$P_{\bot }^{\ast }$
only implicitly through the effective pressure,
![]() ${\mathcal{P}}^{\ast }$
, and the anisotropy function,
${\mathcal{P}}^{\ast }$
, and the anisotropy function,
![]() $\unicode[STIX]{x1D70E}_{d}$
, motivated us to adopt as second equation of state the constrain that the latter function remains constant,
$\unicode[STIX]{x1D70E}_{d}$
, motivated us to adopt as second equation of state the constrain that the latter function remains constant,
![]() $\unicode[STIX]{x1D70E}_{d}^{\ast }=\unicode[STIX]{x1D70E}_{d}=\text{const.}$
,
$\unicode[STIX]{x1D70E}_{d}^{\ast }=\unicode[STIX]{x1D70E}_{d}=\text{const.}$
,
![]() $(\unicode[STIX]{x1D716}=0)$
. This implies that
$(\unicode[STIX]{x1D716}=0)$
. This implies that
![]() $P_{\Vert }^{\ast }$
and
$P_{\Vert }^{\ast }$
and
![]() $P_{\bot }^{\ast }$
(precisely their difference) evolve in such a way that they keep proportional to the magnetic pressure
$P_{\bot }^{\ast }$
(precisely their difference) evolve in such a way that they keep proportional to the magnetic pressure
![]() $B^{2}/(2\unicode[STIX]{x1D707}_{0})$
, which, on physical grounds, is an acceptable approximation. Consequently, equation (3.5) implies that
$B^{2}/(2\unicode[STIX]{x1D707}_{0})$
, which, on physical grounds, is an acceptable approximation. Consequently, equation (3.5) implies that
![]() $G=0$
, while the third of the linearised equations (3.4) reduces to
$G=0$
, while the third of the linearised equations (3.4) reduces to
In view of this relation, we consider incompressible perturbations,
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}=0$
, such that the condition
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D743}=0$
, such that the condition
![]() $\unicode[STIX]{x1D743}\boldsymbol{\cdot }\hat{\boldsymbol{n}}=0$
is satisfied on the boundary. Then, equation (3.6) implies that
$\unicode[STIX]{x1D743}\boldsymbol{\cdot }\hat{\boldsymbol{n}}=0$
is satisfied on the boundary. Then, equation (3.6) implies that
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0$
. Subsequently, the perturbations of the magnetic and velocity fields can be expressed in terms of
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0$
. Subsequently, the perturbations of the magnetic and velocity fields can be expressed in terms of
![]() $\unicode[STIX]{x1D743}$
, as
$\unicode[STIX]{x1D743}$
, as
while the linearised force balance equation of the set (3.4) is put in the form
Here,
is the symmetric force operator and the scalar function
![]() $f$
is defined as
$f$
is defined as
The energy principle is based of the fact that the total perturbation energy
is conserved, where
![]() $K$
is the kinetic energy and
$K$
is the kinetic energy and
![]() $W$
the potential energy. Stability is related to the sign of
$W$
the potential energy. Stability is related to the sign of
![]() $E$
. Since
$E$
. Since
![]() $K$
is quadratic in velocity, and therefore non-negative–definite, a sufficient condition for a given equilibrium to be linearly stable is
$K$
is quadratic in velocity, and therefore non-negative–definite, a sufficient condition for a given equilibrium to be linearly stable is
![]() $W\geqslant 0$
. On account of (3.3)–(3.10),
$W\geqslant 0$
. On account of (3.3)–(3.10),
![]() $W$
is expected to depend only on the physical quantities of the background equilibrium and the displacement vector,
$W$
is expected to depend only on the physical quantities of the background equilibrium and the displacement vector,
![]() $\unicode[STIX]{x1D743}$
, with the exception of the perturbation,
$\unicode[STIX]{x1D743}$
, with the exception of the perturbation,
![]() $p$
, of the effective pressure, appearing in the gradient of the quantity
$p$
, of the effective pressure, appearing in the gradient of the quantity
![]() $f$
. However, the contribution of the latter term to
$f$
. However, the contribution of the latter term to
![]() $W$
vanishes due to the implied boundary conditions on
$W$
vanishes due to the implied boundary conditions on
![]() $\unicode[STIX]{x2202}{\mathcal{D}}$
. Thus, one finds for the perturbation potential energy
$\unicode[STIX]{x2202}{\mathcal{D}}$
. Thus, one finds for the perturbation potential energy
Now we focus our study on the investigation of the linear stability for the equilibria with field-aligned incompressible flows, defined by (2.7). In this case (3.12) becomes
In the next section, we employ the form of
![]() $W$
given in (3.13) to derive a sufficient condition for the linear stability of the respective kinds of equilibria.
$W$
given in (3.13) to derive a sufficient condition for the linear stability of the respective kinds of equilibria.
4 Sufficient condition for linear stability
It is recalled that for equilibria with field-aligned incompressible flows, constant mass density and constant pressure anisotropy function,
![]() $\unicode[STIX]{x1D70E}_{d}$
, defined by (2.7)–(2.13), the current density stays on magnetic surfaces,
$\unicode[STIX]{x1D70E}_{d}$
, defined by (2.7)–(2.13), the current density stays on magnetic surfaces,
![]() $\unicode[STIX]{x1D713}=\text{const.}$
and, thus, the vectors
$\unicode[STIX]{x1D713}=\text{const.}$
and, thus, the vectors
![]() $\boldsymbol{B}$
,
$\boldsymbol{B}$
,
![]() $\boldsymbol{J}$
and
$\boldsymbol{J}$
and
![]() $\boldsymbol{N}=\boldsymbol{B}\times \boldsymbol{J}$
, form a basis in
$\boldsymbol{N}=\boldsymbol{B}\times \boldsymbol{J}$
, form a basis in
![]() $\mathbb{R}^{3}$
space. Accordingly, following the analysis in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007) we expand the displacement vector in this basis, as
$\mathbb{R}^{3}$
space. Accordingly, following the analysis in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007) we expand the displacement vector in this basis, as
where
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D6FE}$
are arbitrary, appropriately dimensional scalar functions. We note that in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007) a sufficient condition was derived for the linear stability of equilibria with field-aligned incompressible flows, isotropic pressure and constant density; in fact, the constant density and the vacuum magnetic permeability constant were set to unity therein. These equilibria are recovered from the respective anisotropic pressure equilibria described in § 2 for
$\unicode[STIX]{x1D6FE}$
are arbitrary, appropriately dimensional scalar functions. We note that in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007) a sufficient condition was derived for the linear stability of equilibria with field-aligned incompressible flows, isotropic pressure and constant density; in fact, the constant density and the vacuum magnetic permeability constant were set to unity therein. These equilibria are recovered from the respective anisotropic pressure equilibria described in § 2 for
![]() $\unicode[STIX]{x1D70E}_{d}=0$
. Also, we observe that the form (3.13) of the potential energy for
$\unicode[STIX]{x1D70E}_{d}=0$
. Also, we observe that the form (3.13) of the potential energy for
![]() $\unicode[STIX]{x1D70E}_{d}=0$
(and
$\unicode[STIX]{x1D70E}_{d}=0$
(and
![]() $\unicode[STIX]{x1D71A}=\unicode[STIX]{x1D707}_{0}=1$
) recovers the one obtained in equation (13) of Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007) for respective isotropic equilibria. Thus, it is straightforward to derive, along the same lines as in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007), a sufficient condition for the linear stability of the present anisotropic equilibria. Specifically, we decompose the potential energy of (3.13) into two integrals as
$\unicode[STIX]{x1D71A}=\unicode[STIX]{x1D707}_{0}=1$
) recovers the one obtained in equation (13) of Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007) for respective isotropic equilibria. Thus, it is straightforward to derive, along the same lines as in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007), a sufficient condition for the linear stability of the present anisotropic equilibria. Specifically, we decompose the potential energy of (3.13) into two integrals as
and, following step by step the procedure in the Appendix of Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007), we obtain
and
where
 $$\begin{eqnarray}\displaystyle {\mathcal{A}} & := & \displaystyle -(1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})\{|\unicode[STIX]{x1D707}_{0}\boldsymbol{J}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}-(\unicode[STIX]{x1D707}_{0}\boldsymbol{J}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713})\boldsymbol{\cdot }[(\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{B}]\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D707}_{0}}{2}[\ln (1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})]^{\prime }|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(P_{\bot }+\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}} & := & \displaystyle -(1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})\{|\unicode[STIX]{x1D707}_{0}\boldsymbol{J}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}-(\unicode[STIX]{x1D707}_{0}\boldsymbol{J}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713})\boldsymbol{\cdot }[(\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{B}]\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D707}_{0}}{2}[\ln (1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})]^{\prime }|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(P_{\bot }+\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}\right).\end{eqnarray}$$
Equations (4.3) and (4.4) imply that
![]() $W$
is non-negative if both quantities
$W$
is non-negative if both quantities
![]() $1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2}$
and
$1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2}$
and
![]() ${\mathcal{A}}$
are also non-negative–definite in
${\mathcal{A}}$
are also non-negative–definite in
![]() ${\mathcal{D}}$
. Thus, we conclude with the following statement: an equilibrium with anisotropic pressure with
${\mathcal{D}}$
. Thus, we conclude with the following statement: an equilibrium with anisotropic pressure with
![]() $\unicode[STIX]{x1D70E}_{d}=\text{const.}$
, of a field-aligned incompressible flow in connection with a constant plasma density is linearly stable if both of the following conditions are satisfied:
$\unicode[STIX]{x1D70E}_{d}=\text{const.}$
, of a field-aligned incompressible flow in connection with a constant plasma density is linearly stable if both of the following conditions are satisfied:
Conditions (4.6) and (4.7) can be applied to any steady state without geometrical restriction. They generalise the ones derived in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007) for isotropic pressure, since for
![]() $\unicode[STIX]{x1D70E}_{d}=0$
condition (4.6) reduces to sub-Afvénic flows,
$\unicode[STIX]{x1D70E}_{d}=0$
condition (4.6) reduces to sub-Afvénic flows,
![]() $\unicode[STIX]{x1D706}^{2}<1$
, while (4.7) reduces to equation (22) in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007). In fact, the expression (4.5) is more compact because it consists of three terms, instead of the four terms in equation (22) of Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007). The first of these terms,
$\unicode[STIX]{x1D706}^{2}<1$
, while (4.7) reduces to equation (22) in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007). In fact, the expression (4.5) is more compact because it consists of three terms, instead of the four terms in equation (22) of Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007). The first of these terms,
is negative and therefore always destabilising, in potential connection with current-driven modes. The second term,
is related to the magnetic shear (i.e. it depends on the variation of
![]() $\boldsymbol{B}$
across the magnetic surfaces), and can be either stabilising or destabilising. The third term,
$\boldsymbol{B}$
across the magnetic surfaces), and can be either stabilising or destabilising. The third term,
can be regarded as a flow term, although it is affected by anisotropy, since it vanishes in the absence of flow (
![]() $\unicode[STIX]{x1D706}=0$
). Note that it relates to the variation of the total pressure perpendicular to the magnetic surfaces; indeed, on account of (2.7) and (2.10) one finds
$\unicode[STIX]{x1D706}=0$
). Note that it relates to the variation of the total pressure perpendicular to the magnetic surfaces; indeed, on account of (2.7) and (2.10) one finds
 $$\begin{eqnarray}P_{\bot }+\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}=\underbrace{{\mathcal{P}}_{s}(\unicode[STIX]{x1D713})}_{\text{static}}-\underbrace{\frac{1}{2}\unicode[STIX]{x1D71A}\boldsymbol{V}^{2}}_{\text{flow}}+\underbrace{(1-\unicode[STIX]{x1D70E}_{d})\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}}_{\text{magnetic}},\end{eqnarray}$$
$$\begin{eqnarray}P_{\bot }+\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}=\underbrace{{\mathcal{P}}_{s}(\unicode[STIX]{x1D713})}_{\text{static}}-\underbrace{\frac{1}{2}\unicode[STIX]{x1D71A}\boldsymbol{V}^{2}}_{\text{flow}}+\underbrace{(1-\unicode[STIX]{x1D70E}_{d})\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}}_{\text{magnetic}},\end{eqnarray}$$
which involves all three pressures, static effective, flow and magnetic, the latter being influenced by the pressure anisotropy through the factor (
![]() $1-\unicode[STIX]{x1D70E}_{d}$
). In addition, satisfaction of condition (4.6) in the absence of flow,
$1-\unicode[STIX]{x1D70E}_{d}$
). In addition, satisfaction of condition (4.6) in the absence of flow,
![]() $\unicode[STIX]{x1D70E}_{d}\leqslant 1$
, implies that the corresponding static anisotropic equilibria are stable under the firehose instability (see Cheviakov & Bogoyavlenskij Reference Cheviakov and Bogoyavlenskij2004).
$\unicode[STIX]{x1D70E}_{d}\leqslant 1$
, implies that the corresponding static anisotropic equilibria are stable under the firehose instability (see Cheviakov & Bogoyavlenskij Reference Cheviakov and Bogoyavlenskij2004).
Before closing this section we note that every equilibrium state with incompressible flow and an anisotropy function that is uniform on the magnetic surfaces,
![]() $\unicode[STIX]{x1D70E}_{d}=\unicode[STIX]{x1D70E}_{d}(\unicode[STIX]{x1D713})$
having certain continuous geometrical symmetry, is governed by a generalised Grad–Shafranov (GS) equation for the flux function
$\unicode[STIX]{x1D70E}_{d}=\unicode[STIX]{x1D70E}_{d}(\unicode[STIX]{x1D713})$
having certain continuous geometrical symmetry, is governed by a generalised Grad–Shafranov (GS) equation for the flux function
![]() $\unicode[STIX]{x1D713}$
, e.g. equation (28) in Evangelias, Kuiroukidis & Throumoulopoulos (Reference Evangelias, Kuiroukidis and Throumoulopoulos2018) governing helically symmetric equilibria. That equation contains a quadratic
$\unicode[STIX]{x1D713}$
, e.g. equation (28) in Evangelias, Kuiroukidis & Throumoulopoulos (Reference Evangelias, Kuiroukidis and Throumoulopoulos2018) governing helically symmetric equilibria. That equation contains a quadratic
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}$
-term. For this reason we have introduced the integral transformation,
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}$
-term. For this reason we have introduced the integral transformation,
under which the respective transformed GS equation, becomes free of a quadratic term as
![]() $|\unicode[STIX]{x1D735}U|^{2}$
, and can be solved by analytical techniques in the
$|\unicode[STIX]{x1D735}U|^{2}$
, and can be solved by analytical techniques in the
![]() $U$
-space. Transformation (4.12) does not change the topology of the magnetic surfaces, but just relabels them by the flux function
$U$
-space. Transformation (4.12) does not change the topology of the magnetic surfaces, but just relabels them by the flux function
![]() $U$
, and consists of a generalisation of the transformation in Clemente (Reference Clemente1993) for static anisotropic equilibria
$U$
, and consists of a generalisation of the transformation in Clemente (Reference Clemente1993) for static anisotropic equilibria
![]() $(\unicode[STIX]{x1D706}=0)$
and that in Simintzis, Throumoulopoulos & Pantis (Reference Simintzis, Throumoulopoulos and Pantis2001) for respective stationary, isotropic equilibria
$(\unicode[STIX]{x1D706}=0)$
and that in Simintzis, Throumoulopoulos & Pantis (Reference Simintzis, Throumoulopoulos and Pantis2001) for respective stationary, isotropic equilibria
![]() $(\unicode[STIX]{x1D70E}_{d}=0)$
. Under transformation (4.12), condition (4.6) is trivially satisfied, while condition (4.7), valid for
$(\unicode[STIX]{x1D70E}_{d}=0)$
. Under transformation (4.12), condition (4.6) is trivially satisfied, while condition (4.7), valid for
![]() $\unicode[STIX]{x1D70E}_{d}=\text{const.}$
, is expressed in
$\unicode[STIX]{x1D70E}_{d}=\text{const.}$
, is expressed in
![]() $U$
-space as
$U$
-space as
 $$\begin{eqnarray}\displaystyle {\mathcal{A}} & = & \displaystyle -|\unicode[STIX]{x1D707}_{0}\boldsymbol{J}\times \unicode[STIX]{x1D735}U|^{2}+(\unicode[STIX]{x1D707}_{0}\boldsymbol{J}\times \unicode[STIX]{x1D735}U)\boldsymbol{\cdot }[(\unicode[STIX]{x1D735}U\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{B}]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D707}_{0}}{2(1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})}\frac{\text{d}\ln (1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})}{\text{d}U}|\unicode[STIX]{x1D735}U|^{2}\unicode[STIX]{x1D735}U\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(P_{\bot }+\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}} & = & \displaystyle -|\unicode[STIX]{x1D707}_{0}\boldsymbol{J}\times \unicode[STIX]{x1D735}U|^{2}+(\unicode[STIX]{x1D707}_{0}\boldsymbol{J}\times \unicode[STIX]{x1D735}U)\boldsymbol{\cdot }[(\unicode[STIX]{x1D735}U\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{B}]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D707}_{0}}{2(1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})}\frac{\text{d}\ln (1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2})}{\text{d}U}|\unicode[STIX]{x1D735}U|^{2}\unicode[STIX]{x1D735}U\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(P_{\bot }+\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}\right).\end{eqnarray}$$
Condition
![]() ${\mathcal{A}}\geqslant 0$
in connection with form (4.13) will be employed in § 6 to examine the stability of specific helically symmetric equilibria.
${\mathcal{A}}\geqslant 0$
in connection with form (4.13) will be employed in § 6 to examine the stability of specific helically symmetric equilibria.
5 Stability under symmetry transformations
In a recent work (Evangelias & Throumoulopoulos Reference Evangelias and Throumoulopoulos2019) a set of symmetry transformations that map anisotropic plasma equilibria with field-aligned incompressible flows was introduced; specifically, these transformations, when applied to a given equilibrium with parallel incompressible flow and anisotropy function,
![]() $\unicode[STIX]{x1D70E}_{d}$
, uniform on the magnetic surfaces labelled by the function
$\unicode[STIX]{x1D70E}_{d}$
, uniform on the magnetic surfaces labelled by the function
![]() $\unicode[STIX]{x1D713}$
,
$\unicode[STIX]{x1D713}$
,
![]() $\{\boldsymbol{B},\unicode[STIX]{x1D71A}(\unicode[STIX]{x1D713}),\boldsymbol{V}=\unicode[STIX]{x1D706}\boldsymbol{B}/(\sqrt{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D71A}}),{\mathcal{P}},\unicode[STIX]{x1D70E}_{d}(\unicode[STIX]{x1D713})\}$
, produce an infinite family of respective equilibria with field-aligned incompressible flows, but a density and anisotropy function that may vary on the magnetic surfaces,
$\{\boldsymbol{B},\unicode[STIX]{x1D71A}(\unicode[STIX]{x1D713}),\boldsymbol{V}=\unicode[STIX]{x1D706}\boldsymbol{B}/(\sqrt{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D71A}}),{\mathcal{P}},\unicode[STIX]{x1D70E}_{d}(\unicode[STIX]{x1D713})\}$
, produce an infinite family of respective equilibria with field-aligned incompressible flows, but a density and anisotropy function that may vary on the magnetic surfaces,
![]() $\{\boldsymbol{B}_{1},\unicode[STIX]{x1D71A}_{1},\boldsymbol{V}_{1},{\mathcal{P}}_{1},\unicode[STIX]{x1D70E}_{d_{1}}\}$
. These transformations are defined by
$\{\boldsymbol{B}_{1},\unicode[STIX]{x1D71A}_{1},\boldsymbol{V}_{1},{\mathcal{P}}_{1},\unicode[STIX]{x1D70E}_{d_{1}}\}$
. These transformations are defined by
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{B}_{1}=\frac{b_{1}(\boldsymbol{r})}{n_{1}(\boldsymbol{r})}\boldsymbol{B},\quad \boldsymbol{V}_{1}=\frac{c_{1}(\boldsymbol{r})\sqrt{1-\unicode[STIX]{x1D70E}_{d}}}{a_{1}(\boldsymbol{r})\sqrt{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D71A}}}\boldsymbol{B},\\ \displaystyle \unicode[STIX]{x1D71A}_{1}(\boldsymbol{r})=a_{1}^{2}(\boldsymbol{r})\unicode[STIX]{x1D71A},\quad {\mathcal{P}}_{1}=C{\mathcal{P}}+(1-\unicode[STIX]{x1D70E}_{d})(C-b_{1}^{2}(\boldsymbol{r}))\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}},\\ \displaystyle \unicode[STIX]{x1D70E}_{d_{1}}=1-n_{1}^{2}(\boldsymbol{r})(1-\unicode[STIX]{x1D70E}_{d}),\quad C=\frac{[b_{1}^{2}(\boldsymbol{r})-c_{1}^{2}(\boldsymbol{r})](1-\unicode[STIX]{x1D70E}_{d})}{1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2}}=\text{const.}\neq 0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{B}_{1}=\frac{b_{1}(\boldsymbol{r})}{n_{1}(\boldsymbol{r})}\boldsymbol{B},\quad \boldsymbol{V}_{1}=\frac{c_{1}(\boldsymbol{r})\sqrt{1-\unicode[STIX]{x1D70E}_{d}}}{a_{1}(\boldsymbol{r})\sqrt{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D71A}}}\boldsymbol{B},\\ \displaystyle \unicode[STIX]{x1D71A}_{1}(\boldsymbol{r})=a_{1}^{2}(\boldsymbol{r})\unicode[STIX]{x1D71A},\quad {\mathcal{P}}_{1}=C{\mathcal{P}}+(1-\unicode[STIX]{x1D70E}_{d})(C-b_{1}^{2}(\boldsymbol{r}))\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}},\\ \displaystyle \unicode[STIX]{x1D70E}_{d_{1}}=1-n_{1}^{2}(\boldsymbol{r})(1-\unicode[STIX]{x1D70E}_{d}),\quad C=\frac{[b_{1}^{2}(\boldsymbol{r})-c_{1}^{2}(\boldsymbol{r})](1-\unicode[STIX]{x1D70E}_{d})}{1-\unicode[STIX]{x1D70E}_{d}-\unicode[STIX]{x1D706}^{2}}=\text{const.}\neq 0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
![]() $a_{1},b_{1},c_{1}$
and
$a_{1},b_{1},c_{1}$
and
![]() $n_{1}$
are scalar functions, which must satisfy the relations
$n_{1}$
are scalar functions, which must satisfy the relations
Transformations (5.1), consisting a generalisation of those introduced in Bogoyavlenskij (Reference Bogoyavlenskij2001) for respective equilibria with isotropic pressure, preserve the topology of the magnetic surfaces,
![]() $\unicode[STIX]{x1D713}\equiv \unicode[STIX]{x1D713}_{1}=\text{const.}$
, between the original and the transformed equilibrium, i.e.
$\unicode[STIX]{x1D713}\equiv \unicode[STIX]{x1D713}_{1}=\text{const.}$
, between the original and the transformed equilibrium, i.e.
![]() $\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}=\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$
. It was also proved in Evangelias & Throumoulopoulos (Reference Evangelias and Throumoulopoulos2019) that these transformations can break the geometrical symmetry of a given equilibrium only when the fields
$\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}=\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$
. It was also proved in Evangelias & Throumoulopoulos (Reference Evangelias and Throumoulopoulos2019) that these transformations can break the geometrical symmetry of a given equilibrium only when the fields
![]() $\boldsymbol{B}$
and
$\boldsymbol{B}$
and
![]() $\boldsymbol{V}$
are purely poloidal.
$\boldsymbol{V}$
are purely poloidal.
From (5.1) it readily follows that the transformed collinear velocity and magnetic fields are related through
and thus, the transformed equilibria satisfy a force balance equation analogous to (2.8)
 $$\begin{eqnarray}\displaystyle & & \displaystyle (1-\unicode[STIX]{x1D70E}_{d_{1}}-\unicode[STIX]{x1D706}_{1}^{2})\boldsymbol{J}_{1}\times \boldsymbol{B}_{1}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D735}\left({\mathcal{P}}_{1}+\unicode[STIX]{x1D706}_{1}^{2}\frac{\boldsymbol{B}_{1}^{2}}{2\unicode[STIX]{x1D707}_{0}}\right)+\frac{\boldsymbol{B}_{1}^{2}}{2\unicode[STIX]{x1D707}_{0}}\unicode[STIX]{x1D735}(1-\unicode[STIX]{x1D70E}_{d_{1}}-\unicode[STIX]{x1D706}_{1}^{2})-\frac{\boldsymbol{B}_{1}}{\unicode[STIX]{x1D707}_{0}}[\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(1-\unicode[STIX]{x1D70E}_{d_{1}}-\unicode[STIX]{x1D706}_{1}^{2})].\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (1-\unicode[STIX]{x1D70E}_{d_{1}}-\unicode[STIX]{x1D706}_{1}^{2})\boldsymbol{J}_{1}\times \boldsymbol{B}_{1}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D735}\left({\mathcal{P}}_{1}+\unicode[STIX]{x1D706}_{1}^{2}\frac{\boldsymbol{B}_{1}^{2}}{2\unicode[STIX]{x1D707}_{0}}\right)+\frac{\boldsymbol{B}_{1}^{2}}{2\unicode[STIX]{x1D707}_{0}}\unicode[STIX]{x1D735}(1-\unicode[STIX]{x1D70E}_{d_{1}}-\unicode[STIX]{x1D706}_{1}^{2})-\frac{\boldsymbol{B}_{1}}{\unicode[STIX]{x1D707}_{0}}[\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(1-\unicode[STIX]{x1D70E}_{d_{1}}-\unicode[STIX]{x1D706}_{1}^{2})].\qquad\end{eqnarray}$$
With the aid of (5.1) and (5.3) we obtain the useful relations
under which equation (5.4) reduces to
Now, presume that the original equilibrium belongs to the family described in § 2 for which (2.11) holds; then (5.7) becomes
Projection of (5.8) along
![]() $\boldsymbol{J}_{1}$
yields
$\boldsymbol{J}_{1}$
yields
and thus, it turns out that the transformed current density,
![]() $\boldsymbol{J}_{1}$
, remains on the magnetic surfaces if and only if the ratio
$\boldsymbol{J}_{1}$
, remains on the magnetic surfaces if and only if the ratio
![]() $n_{1}/b_{1}$
is uniform on those surfaces
$n_{1}/b_{1}$
is uniform on those surfaces
In this case, the transformed vectors,
![]() $\boldsymbol{J}_{1},\boldsymbol{B}_{1}$
, and
$\boldsymbol{J}_{1},\boldsymbol{B}_{1}$
, and
![]() $\boldsymbol{N}_{1}\equiv \boldsymbol{J}_{1}\times \boldsymbol{B}_{1}$
, form a basis in
$\boldsymbol{N}_{1}\equiv \boldsymbol{J}_{1}\times \boldsymbol{B}_{1}$
, form a basis in
![]() $\mathbb{R}^{3}$
, and thus, for constant
$\mathbb{R}^{3}$
, and thus, for constant
![]() $\unicode[STIX]{x1D71A}_{1}$
and
$\unicode[STIX]{x1D71A}_{1}$
and
![]() $\unicode[STIX]{x1D70E}_{d_{1}}$
, sufficient conditions for the linear stability of the transformed equilibria, satisfying (5.1), (5.3) and (5.10), analogous to (4.6) and (4.7) can be derived
$\unicode[STIX]{x1D70E}_{d_{1}}$
, sufficient conditions for the linear stability of the transformed equilibria, satisfying (5.1), (5.3) and (5.10), analogous to (4.6) and (4.7) can be derived
where
 $$\begin{eqnarray}\displaystyle {\mathcal{A}}_{1} & = & \displaystyle -(1-\unicode[STIX]{x1D70E}_{d_{1}}-\unicode[STIX]{x1D706}_{1}^{2})\{|\unicode[STIX]{x1D707}_{0}\boldsymbol{J}_{1}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}+(\unicode[STIX]{x1D707}_{0}\boldsymbol{J}_{1}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713})\boldsymbol{\cdot }[(\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{B}_{1}]\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D707}_{0}}{2}[\ln (1-\unicode[STIX]{x1D70E}_{d_{1}}-\unicode[STIX]{x1D706}_{1}^{2})]^{\prime }|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\mathcal{P}}_{\bot _{1}}+\frac{\boldsymbol{B}_{1}^{2}}{2\unicode[STIX]{x1D707}_{0}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{1} & = & \displaystyle -(1-\unicode[STIX]{x1D70E}_{d_{1}}-\unicode[STIX]{x1D706}_{1}^{2})\{|\unicode[STIX]{x1D707}_{0}\boldsymbol{J}_{1}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}+(\unicode[STIX]{x1D707}_{0}\boldsymbol{J}_{1}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713})\boldsymbol{\cdot }[(\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{B}_{1}]\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D707}_{0}}{2}[\ln (1-\unicode[STIX]{x1D70E}_{d_{1}}-\unicode[STIX]{x1D706}_{1}^{2})]^{\prime }|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\mathcal{P}}_{\bot _{1}}+\frac{\boldsymbol{B}_{1}^{2}}{2\unicode[STIX]{x1D707}_{0}}\right).\end{eqnarray}$$
In order to investigate the stability of the aforementioned transformed equilibria, we presume that the original equilibrium has constant density and anisotropy functions (
![]() $\unicode[STIX]{x1D71A}=\text{const.}$
,
$\unicode[STIX]{x1D71A}=\text{const.}$
,
![]() $\unicode[STIX]{x1D70E}_{d}=\text{const.}$
) and is stable under small three-dimensional perturbations; therefore, conditions (4.6) and (4.7) are satisfied in
$\unicode[STIX]{x1D70E}_{d}=\text{const.}$
) and is stable under small three-dimensional perturbations; therefore, conditions (4.6) and (4.7) are satisfied in
![]() ${\mathcal{D}}$
. Note that in this case the scalar functions of transformation (5.1) must have a structure of the form:
${\mathcal{D}}$
. Note that in this case the scalar functions of transformation (5.1) must have a structure of the form:
![]() $a_{1}=\text{const.}$
,
$a_{1}=\text{const.}$
,
![]() $n_{1}=\text{const.}$
,
$n_{1}=\text{const.}$
,
![]() $b_{1}=b_{1}(\unicode[STIX]{x1D713})$
,
$b_{1}=b_{1}(\unicode[STIX]{x1D713})$
,
![]() $c_{1}=c_{1}(\unicode[STIX]{x1D713})$
; as a result, breaking potential geometrical symmetry of the original equilibrium is not possible by the transformation even for purely poloidal
$c_{1}=c_{1}(\unicode[STIX]{x1D713})$
; as a result, breaking potential geometrical symmetry of the original equilibrium is not possible by the transformation even for purely poloidal
![]() $\boldsymbol{B}$
and
$\boldsymbol{B}$
and
![]() $\boldsymbol{V}$
fields. In Ilin & Vladimirov (Reference Ilin and Vladimirov2004) the stability of respective isotropic equilibria was examined; in particular, it was stated therein that all equilibrium families resulting from the application of the respective isotropic transformations introduced by Bogoyavlenskij to given equilibria of field-aligned incompressible flows, with isotropic pressure and constant mass density, are linearly stable, if either the original equilibria is stable and
$\boldsymbol{V}$
fields. In Ilin & Vladimirov (Reference Ilin and Vladimirov2004) the stability of respective isotropic equilibria was examined; in particular, it was stated therein that all equilibrium families resulting from the application of the respective isotropic transformations introduced by Bogoyavlenskij to given equilibria of field-aligned incompressible flows, with isotropic pressure and constant mass density, are linearly stable, if either the original equilibria is stable and
![]() $C>0$
, or the original equilibria is unstable and
$C>0$
, or the original equilibria is unstable and
![]() $C<0$
. A straightforward calculation shows that
$C<0$
. A straightforward calculation shows that
so that conditions (5.11) and (5.12) assume the form
By inspection of the later relations, we come to the conclusion that the transformed equilibrium is linearly stable if, either (i) the original one is linearly stable and
![]() $C>0$
, or (ii) neither of the conditions (4.6), (4.7) are satisfied and
$C>0$
, or (ii) neither of the conditions (4.6), (4.7) are satisfied and
![]() $C<0$
. However, when
$C<0$
. However, when
![]() $C$
is negative equation (5.6) in the absence of flow
$C$
is negative equation (5.6) in the absence of flow
![]() $(\unicode[STIX]{x1D706}=0)$
yields the physically unacceptable relation
$(\unicode[STIX]{x1D706}=0)$
yields the physically unacceptable relation
Thus, we finally conclude with the formulation of the following statement:
The infinite class of equilibria, obtained from the application of the symmetry transformations (5.1) for the case
![]() $\unicode[STIX]{x1D71A}_{1}=\text{const.}$
and
$\unicode[STIX]{x1D71A}_{1}=\text{const.}$
and
![]() $\unicode[STIX]{x1D70E}_{d_{1}}=\text{const.}$
to given respective equilibria which are linearly stable (by satisfying the sufficient conditions (4.6)–(4.7)), are also linearly stable if the transformation constant
$\unicode[STIX]{x1D70E}_{d_{1}}=\text{const.}$
to given respective equilibria which are linearly stable (by satisfying the sufficient conditions (4.6)–(4.7)), are also linearly stable if the transformation constant
![]() $C$
is positive definite.
$C$
is positive definite.
This statement corrects and generalises the respective statement in Ilin & Vladimirov (Reference Ilin and Vladimirov2004) for isotropic equilibria
![]() $(\unicode[STIX]{x1D70E}_{d}=\unicode[STIX]{x1D70E}_{d_{1}}=0,n_{1}=1)$
.
$(\unicode[STIX]{x1D70E}_{d}=\unicode[STIX]{x1D70E}_{d_{1}}=0,n_{1}=1)$
.
6 Linear stability of helically symmetric equilibria
In this section we consider helically symmetric equilibria with field-aligned incompressible flows and the anisotropic pressure derived in Evangelias et al. (Reference Evangelias, Kuiroukidis and Throumoulopoulos2018), for which the following relations hold:
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{B}=I(U)\boldsymbol{h}+(1-\unicode[STIX]{x1D70E}_{d}-M_{p}(U)^{2})^{-1/2}\boldsymbol{h}\times \unicode[STIX]{x1D735}U(r,u),\quad \boldsymbol{V}=\frac{M_{p}(U)}{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D71A}}\boldsymbol{B},\\ \displaystyle \unicode[STIX]{x1D71A}=\text{const.},\quad \unicode[STIX]{x1D70E}_{d}=\text{const.},\quad {\mathcal{P}}={\mathcal{P}}_{s}(U)-M_{p}^{2}(U)\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{B}=I(U)\boldsymbol{h}+(1-\unicode[STIX]{x1D70E}_{d}-M_{p}(U)^{2})^{-1/2}\boldsymbol{h}\times \unicode[STIX]{x1D735}U(r,u),\quad \boldsymbol{V}=\frac{M_{p}(U)}{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D71A}}\boldsymbol{B},\\ \displaystyle \unicode[STIX]{x1D71A}=\text{const.},\quad \unicode[STIX]{x1D70E}_{d}=\text{const.},\quad {\mathcal{P}}={\mathcal{P}}_{s}(U)-M_{p}^{2}(U)\frac{\boldsymbol{B}^{2}}{2\unicode[STIX]{x1D707}_{0}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Here, the function
![]() $U(r,u)$
labels the magnetic surfaces, where
$U(r,u)$
labels the magnetic surfaces, where
![]() $(r,u,z)$
are helical coordinates defined through the usual cylindrical ones
$(r,u,z)$
are helical coordinates defined through the usual cylindrical ones
![]() $(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},\unicode[STIX]{x1D701})$
as
$(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D719},\unicode[STIX]{x1D701})$
as
![]() $r=\unicode[STIX]{x1D70C}$
,
$r=\unicode[STIX]{x1D70C}$
,
![]() $u=z-\unicode[STIX]{x1D702}\unicode[STIX]{x1D719}$
,
$u=z-\unicode[STIX]{x1D702}\unicode[STIX]{x1D719}$
,
![]() $z=\unicode[STIX]{x1D701}$
;
$z=\unicode[STIX]{x1D701}$
;
![]() $I$
relates to the helicoidal magnetic field;
$I$
relates to the helicoidal magnetic field;
![]() ${\mathcal{P}}_{s}$
is the static effective pressure;
${\mathcal{P}}_{s}$
is the static effective pressure;
![]() $M_{p}$
is the Alfvén Mach function for the poloidal field, defined as
$M_{p}$
is the Alfvén Mach function for the poloidal field, defined as
![]() $M_{p}:=(\sqrt{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D71A}}|\boldsymbol{V}_{pol}|)/\boldsymbol{B}_{pol}$
, which for parallel flows equals to the total Mach function
$M_{p}:=(\sqrt{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D71A}}|\boldsymbol{V}_{pol}|)/\boldsymbol{B}_{pol}$
, which for parallel flows equals to the total Mach function
![]() $(M=\unicode[STIX]{x1D706}=\sqrt{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D71A}}|\boldsymbol{V}|/\boldsymbol{B})$
. All these functions are uniform on the magnetic surfaces. In addition, the vector
$(M=\unicode[STIX]{x1D706}=\sqrt{\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D71A}}|\boldsymbol{V}|/\boldsymbol{B})$
. All these functions are uniform on the magnetic surfaces. In addition, the vector
![]() $\boldsymbol{h}:=(-\unicode[STIX]{x1D702}/(k^{2}r^{2}+\unicode[STIX]{x1D702}^{2}))\boldsymbol{g}_{z}$
points along the helical direction, where
$\boldsymbol{h}:=(-\unicode[STIX]{x1D702}/(k^{2}r^{2}+\unicode[STIX]{x1D702}^{2}))\boldsymbol{g}_{z}$
points along the helical direction, where
![]() $\unicode[STIX]{x1D702}$
is an arbitrary constant, and
$\unicode[STIX]{x1D702}$
is an arbitrary constant, and
![]() $\boldsymbol{g}_{i}=\unicode[STIX]{x2202}\boldsymbol{r}/\unicode[STIX]{x2202}i~(i=r,u,z)$
are the covariant helical basis vectors. According to Evangelias et al. (Reference Evangelias, Kuiroukidis and Throumoulopoulos2018), equilibria (6.1) are governed by the following generalised GS equation
$\boldsymbol{g}_{i}=\unicode[STIX]{x2202}\boldsymbol{r}/\unicode[STIX]{x2202}i~(i=r,u,z)$
are the covariant helical basis vectors. According to Evangelias et al. (Reference Evangelias, Kuiroukidis and Throumoulopoulos2018), equilibria (6.1) are governed by the following generalised GS equation
where the elliptic operator involved is defined as
![]() ${\mathcal{L}}:=(r^{2}+\unicode[STIX]{x1D702}^{2})[\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}/(r^{2}+\unicode[STIX]{x1D702}^{2}))]$
. In fact, equation (6.2) constitutes a reduced form of the more general one (Evangelias et al. (Reference Evangelias, Kuiroukidis and Throumoulopoulos2018), equation (30)) valid in general for non-collinear
${\mathcal{L}}:=(r^{2}+\unicode[STIX]{x1D702}^{2})[\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}/(r^{2}+\unicode[STIX]{x1D702}^{2}))]$
. In fact, equation (6.2) constitutes a reduced form of the more general one (Evangelias et al. (Reference Evangelias, Kuiroukidis and Throumoulopoulos2018), equation (30)) valid in general for non-collinear
![]() $\boldsymbol{V}$
and
$\boldsymbol{V}$
and
![]() $\boldsymbol{B}$
, with the replacement of the parameters
$\boldsymbol{B}$
, with the replacement of the parameters
![]() $m$
and
$m$
and
![]() $k$
therein by
$k$
therein by
![]() $-\unicode[STIX]{x1D702}$
and
$-\unicode[STIX]{x1D702}$
and
![]() $-1$
, respectively, here. Under the following linearising ansatz for the free function terms,
$-1$
, respectively, here. Under the following linearising ansatz for the free function terms,
the GS equation (6.2) reduces to the form
where
![]() $w_{1},w_{2}$
and
$w_{1},w_{2}$
and
![]() $w_{3}$
are arbitrary constants. Partial differential equation (PDE) (6.4) was solved analytically in Bogoyavlenskij (Reference Bogoyavlenskij2000) and the exact solution obtained therein is
$w_{3}$
are arbitrary constants. Partial differential equation (PDE) (6.4) was solved analytically in Bogoyavlenskij (Reference Bogoyavlenskij2000) and the exact solution obtained therein is
where
![]() $N,q,l$
are arbitrary integers
$N,q,l$
are arbitrary integers
![]() ${\geqslant}0$
satisfying the condition
${\geqslant}0$
satisfying the condition
![]() $2N>2l+q$
;
$2N>2l+q$
;
![]() $f_{N},c_{ql},d_{ql}$
are arbitrary coefficients, and
$f_{N},c_{ql},d_{ql}$
are arbitrary coefficients, and
![]() $s=2w_{3}r^{2}$
; the form of the polynomial functions
$s=2w_{3}r^{2}$
; the form of the polynomial functions
![]() $R_{ql}(s)$
involves derivatives of the Laguerre polynomials
$R_{ql}(s)$
involves derivatives of the Laguerre polynomials
![]() $L_{q+l}(s)$
(see Bogoyavlenskij (Reference Bogoyavlenskij2000), equations (3.7)–(3.8)), and
$L_{q+l}(s)$
(see Bogoyavlenskij (Reference Bogoyavlenskij2000), equations (3.7)–(3.8)), and
![]() $R_{0N}$
is the respective polynomial for
$R_{0N}$
is the respective polynomial for
![]() $q=0$
,
$q=0$
,
![]() $l=N\neq 0$
. On account of solution (6.5), different classes of exact helically symmetric MHD equilibria describing astrophysical jets with isotropic pressure
$l=N\neq 0$
. On account of solution (6.5), different classes of exact helically symmetric MHD equilibria describing astrophysical jets with isotropic pressure
![]() $(\unicode[STIX]{x1D70E}_{d}=0)$
were constructed in Bogoyavlenskij (Reference Bogoyavlenskij2000). For such equilibria, the magnetic field, the flow velocity and the current density fall rapidly to zero at
$(\unicode[STIX]{x1D70E}_{d}=0)$
were constructed in Bogoyavlenskij (Reference Bogoyavlenskij2000). For such equilibria, the magnetic field, the flow velocity and the current density fall rapidly to zero at
![]() $r\rightarrow \infty$
, while the pertinent isotropic pressure takes a limiting constant value therein. We have to note that solution (6.5) can also accurately describe helically symmetric CGL anisotropic pressure equilibria, with
$r\rightarrow \infty$
, while the pertinent isotropic pressure takes a limiting constant value therein. We have to note that solution (6.5) can also accurately describe helically symmetric CGL anisotropic pressure equilibria, with
![]() $\unicode[STIX]{x1D70E}_{d}$
being a surface quantity (or constant), and incompressible flow. This is due to the fact that although the MHD and CGL models are established through different physical assumptions for the particle collisions, the form of the generalised GS equations governing them are identical, such that passing from the one equilibrium equation to the other is mathematically convenient.
$\unicode[STIX]{x1D70E}_{d}$
being a surface quantity (or constant), and incompressible flow. This is due to the fact that although the MHD and CGL models are established through different physical assumptions for the particle collisions, the form of the generalised GS equations governing them are identical, such that passing from the one equilibrium equation to the other is mathematically convenient.

Figure 1. Poloidal cut of helicoidal magnetic surfaces
![]() $U(x,y,z=0)=\text{const}$
. for the helically symmetric equilibrium solution (6.6).
$U(x,y,z=0)=\text{const}$
. for the helically symmetric equilibrium solution (6.6).

Figure 2. Profile of the function
![]() $U(x,y=0,z=0)=\text{const.}$
for the helically symmetric equilibrium solution (6.6).
$U(x,y=0,z=0)=\text{const.}$
for the helically symmetric equilibrium solution (6.6).

Figure 3. The profiles of the scalar pressures (a)
![]() $P_{\bot }(x,y=0,z=0)$
and (b)
$P_{\bot }(x,y=0,z=0)$
and (b)
![]() $P_{\Vert }(x,y=0,z=0)$
for the constructed stationary equilibria, for
$P_{\Vert }(x,y=0,z=0)$
for the constructed stationary equilibria, for
![]() $M_{p_{0}}^{2}=10^{-3}$
. The blue dashed curve corresponds to
$M_{p_{0}}^{2}=10^{-3}$
. The blue dashed curve corresponds to
![]() $\unicode[STIX]{x1D70E}_{d}=0.1$
, while the red dotted one to
$\unicode[STIX]{x1D70E}_{d}=0.1$
, while the red dotted one to
![]() $\unicode[STIX]{x1D70E}_{d}=-0.1$
.
$\unicode[STIX]{x1D70E}_{d}=-0.1$
.
In order to construct specific equilibria, we restrict our analysis to solution (6.5) for
![]() $N=2,q=1,l=0$
and
$N=2,q=1,l=0$
and
![]() $w_{1}=7/(6\unicode[STIX]{x1D702})$
, which assumes the simpler form (see Bogoyavlenskij (Reference Bogoyavlenskij2000), equation (4.2))
$w_{1}=7/(6\unicode[STIX]{x1D702})$
, which assumes the simpler form (see Bogoyavlenskij (Reference Bogoyavlenskij2000), equation (4.2))
Solution (6.6) of the GS equation (6.2), associated with the relations (6.1) and the profiles (6.3), defines a special class of exact helically symmetric equilibria with incompressible flows with constant density and anisotropy functions, valid for any functional dependence of
![]() $M_{p}^{2}(U)$
. Therefore, to completely determine an equilibrium, we employ the following profile for the Mach function:
$M_{p}^{2}(U)$
. Therefore, to completely determine an equilibrium, we employ the following profile for the Mach function:
where
![]() $M_{p_{0}}$
is an arbitrary parameter. The magnetic surfaces of the above constructed equilibria on the Cartesian plane
$M_{p_{0}}$
is an arbitrary parameter. The magnetic surfaces of the above constructed equilibria on the Cartesian plane
![]() $z=0$
, for
$z=0$
, for
![]() $w_{3}=0.01,c_{10}=0.5,w_{2}=2$
and
$w_{3}=0.01,c_{10}=0.5,w_{2}=2$
and
![]() $\unicode[STIX]{x1D702}=2.318$
, are shown in figure 1; all dimensional quantities present in this section are measured in appropriate SI units. Also, the profile of the flux function
$\unicode[STIX]{x1D702}=2.318$
, are shown in figure 1; all dimensional quantities present in this section are measured in appropriate SI units. Also, the profile of the flux function
![]() $U$
along the
$U$
along the
![]() $x$
-axis is given in figure 2. In figures 1 and 2 it can be seen that the plasma domain consists of two sub-domains: an outer one consisting of magnetic surfaces with circular poloidal cross-sections extending up to infinity (
$x$
-axis is given in figure 2. In figures 1 and 2 it can be seen that the plasma domain consists of two sub-domains: an outer one consisting of magnetic surfaces with circular poloidal cross-sections extending up to infinity (
![]() $r\rightarrow \infty$
), and an inner sub-domain containing three lobes and a couple of saddle points (X-points). The inner X-point, corresponding to a maximum of
$r\rightarrow \infty$
), and an inner sub-domain containing three lobes and a couple of saddle points (X-points). The inner X-point, corresponding to a maximum of
![]() $U$
, is located at
$U$
, is located at
![]() $x=-17.6$
. Then on the right-hand side of this first X-point are located, successively, two lobes, then the second X-point and farther outwards the third lob. The respective magnetic axes of the lobes are located at
$x=-17.6$
. Then on the right-hand side of this first X-point are located, successively, two lobes, then the second X-point and farther outwards the third lob. The respective magnetic axes of the lobes are located at
![]() $x=-7.07$
,
$x=-7.07$
,
![]() $x=2.31$
and
$x=2.31$
and
![]() $x=15.3$
while the second X-point is located at
$x=15.3$
while the second X-point is located at
![]() $x=7.07$
. Each helix composing such a helically symmetric configuration is characterised by a pitch length, equal to
$x=7.07$
. Each helix composing such a helically symmetric configuration is characterised by a pitch length, equal to
![]() $2\unicode[STIX]{x03C0}\unicode[STIX]{x1D702}$
, and a torsion given by
$2\unicode[STIX]{x03C0}\unicode[STIX]{x1D702}$
, and a torsion given by
The above equilibrium can model helically symmetric jets with anisotropic pressure, tending to become isotropic at very long distances (
![]() $r\rightarrow \infty$
). In more detail, for any
$r\rightarrow \infty$
). In more detail, for any
![]() $\unicode[STIX]{x1D70E}_{d}=\text{const.}\neq 0$
inside
$\unicode[STIX]{x1D70E}_{d}=\text{const.}\neq 0$
inside
![]() ${\mathcal{D}}$
, the scalar pressures parallel and perpendicular to
${\mathcal{D}}$
, the scalar pressures parallel and perpendicular to
![]() $\boldsymbol{B}$
are given by the relations
$\boldsymbol{B}$
are given by the relations
indicating that when
![]() $\unicode[STIX]{x1D70E}_{d}>0$
, its increase results in an enhancement of
$\unicode[STIX]{x1D70E}_{d}>0$
, its increase results in an enhancement of
![]() $P_{\bot }$
while
$P_{\bot }$
while
![]() $P_{\Vert }$
decreases, and vice versa for
$P_{\Vert }$
decreases, and vice versa for
![]() $\unicode[STIX]{x1D70E}_{d}<0$
, as can be seen at the profiles of
$\unicode[STIX]{x1D70E}_{d}<0$
, as can be seen at the profiles of
![]() $P_{\Vert }$
and
$P_{\Vert }$
and
![]() $P_{\bot }$
shown in figure 3. In the limit of
$P_{\bot }$
shown in figure 3. In the limit of
![]() $r\rightarrow \infty$
the magnetic field, current density and velocity vanish and therefore the scalar pressures become equal to each other, i.e.
$r\rightarrow \infty$
the magnetic field, current density and velocity vanish and therefore the scalar pressures become equal to each other, i.e.
![]() $P_{\bot }=P_{\Vert }=w_{2}=\text{const.}$
because of the second of (6.3) and (6.9). Thus, the configuration becomes, in this limit, isotropic. Note that this is compatible with a non-zero value of
$P_{\bot }=P_{\Vert }=w_{2}=\text{const.}$
because of the second of (6.3) and (6.9). Thus, the configuration becomes, in this limit, isotropic. Note that this is compatible with a non-zero value of
![]() $\unicode[STIX]{x1D70E}_{d}$
on account of the definition (2.3), which makes
$\unicode[STIX]{x1D70E}_{d}$
on account of the definition (2.3), which makes
![]() $\unicode[STIX]{x1D70E}_{d}$
indefinite in the limit of
$\unicode[STIX]{x1D70E}_{d}$
indefinite in the limit of
![]() $r\rightarrow \infty$
. Profiles of the magnetic field magnitude,
$r\rightarrow \infty$
. Profiles of the magnetic field magnitude,
![]() $B$
, and the helicoidal component of the current density,
$B$
, and the helicoidal component of the current density,
![]() $J_{h}$
, are shown in figure 4. The values of
$J_{h}$
, are shown in figure 4. The values of
![]() $B$
become greater (lower) for
$B$
become greater (lower) for
![]() $\unicode[STIX]{x1D70E}_{d}>0$
(
$\unicode[STIX]{x1D70E}_{d}>0$
(
![]() $\unicode[STIX]{x1D70E}_{d}<0$
), in connection with a diamagnetic (paramagnetic) behaviour. The helicoidal current density,
$\unicode[STIX]{x1D70E}_{d}<0$
), in connection with a diamagnetic (paramagnetic) behaviour. The helicoidal current density,
![]() $J_{h}$
, reverses near the origin and becomes more peaked (hollow) for
$J_{h}$
, reverses near the origin and becomes more peaked (hollow) for
![]() $\unicode[STIX]{x1D70E}_{d}>0$
(
$\unicode[STIX]{x1D70E}_{d}>0$
(
![]() $\unicode[STIX]{x1D70E}_{d}<0$
). In addition, profiles of the helicoidal velocity component,
$\unicode[STIX]{x1D70E}_{d}<0$
). In addition, profiles of the helicoidal velocity component,
![]() $V_{h}$
and the Mach function,
$V_{h}$
and the Mach function,
![]() $M_{p}^{2}$
, are provided in figure 5. It is noted that
$M_{p}^{2}$
, are provided in figure 5. It is noted that
![]() $V_{h}$
reverses in the region of the left lobe, where
$V_{h}$
reverses in the region of the left lobe, where
![]() $U$
becomes negative, and that the flow in terms of the Mach function,
$U$
becomes negative, and that the flow in terms of the Mach function,
![]() $M_{p}^{2}$
, strengthens the impact of pressure anisotropy for
$M_{p}^{2}$
, strengthens the impact of pressure anisotropy for
![]() $\unicode[STIX]{x1D70E}_{d}>0$
, due to the factor
$\unicode[STIX]{x1D70E}_{d}>0$
, due to the factor
![]() $1-\unicode[STIX]{x1D70E}_{d}-M_{p}^{2}$
(cf. (6.2)). In this respect, it is expected that the increase of the parameter
$1-\unicode[STIX]{x1D70E}_{d}-M_{p}^{2}$
(cf. (6.2)). In this respect, it is expected that the increase of the parameter
![]() $M_{p_{0}}^{2}$
has the same impact on
$M_{p_{0}}^{2}$
has the same impact on
![]() $V_{h}$
as that shown in figure 5(a) for
$V_{h}$
as that shown in figure 5(a) for
![]() $\unicode[STIX]{x1D70E}_{d}>0$
.
$\unicode[STIX]{x1D70E}_{d}>0$
.

Figure 4. Variation of (a)
![]() $|\boldsymbol{B}(x,y=0,z=0)|$
and (b)
$|\boldsymbol{B}(x,y=0,z=0)|$
and (b)
![]() $J_{h}(x,y=0,z=0)$
, for the stationary equilibria constructed here, for
$J_{h}(x,y=0,z=0)$
, for the stationary equilibria constructed here, for
![]() $M_{p_{0}}^{2}=10^{-3}$
and the impact of pressure anisotropy on them for positive and negative values of
$M_{p_{0}}^{2}=10^{-3}$
and the impact of pressure anisotropy on them for positive and negative values of
![]() $\unicode[STIX]{x1D70E}_{d}$
.
$\unicode[STIX]{x1D70E}_{d}$
.

Figure 5. Profiles of (a) the helicoidal velocity component for
![]() $M_{p_{0}}^{2}=0.06$
, and the impact of pressure anisotropy through
$M_{p_{0}}^{2}=0.06$
, and the impact of pressure anisotropy through
![]() $\unicode[STIX]{x1D70E}_{d}$
, and (b) the Mach function along the
$\unicode[STIX]{x1D70E}_{d}$
, and (b) the Mach function along the
![]() $x$
-axis for different values of the flow parameter
$x$
-axis for different values of the flow parameter
![]() $M_{p_{0}}^{2}$
.
$M_{p_{0}}^{2}$
.
In what follows, we employ the derived suffiecient condition by calculating the quantity
![]() ${\mathcal{A}}=A_{1}+A_{2}+A_{3}$
of (4.13) (in connection with (4.5), (4.8)–(4.10) in the
${\mathcal{A}}=A_{1}+A_{2}+A_{3}$
of (4.13) (in connection with (4.5), (4.8)–(4.10) in the
![]() $\unicode[STIX]{x1D713}$
-space) for the helically symmetric equilibria, defined by the relations (6.1), (6.3) and (6.6)–(6.9), in order to examine the impact of the pressure anisotropy, flow and torsion on their linear stability, through the variation of the parameters
$\unicode[STIX]{x1D713}$
-space) for the helically symmetric equilibria, defined by the relations (6.1), (6.3) and (6.6)–(6.9), in order to examine the impact of the pressure anisotropy, flow and torsion on their linear stability, through the variation of the parameters
![]() $\unicode[STIX]{x1D70E}_{d},M_{p_{0}}$
and
$\unicode[STIX]{x1D70E}_{d},M_{p_{0}}$
and
![]() $\unicode[STIX]{x1D702}$
, respectively. We recall that the aforementioned relations were obtained by applying the integral transformation (4.12) (see Evangelias et al.
Reference Evangelias, Kuiroukidis and Throumoulopoulos2018); in this respect the condition (4.6) is trivially satisfied. Figure 6(a) shows that the condition
$\unicode[STIX]{x1D702}$
, respectively. We recall that the aforementioned relations were obtained by applying the integral transformation (4.12) (see Evangelias et al.
Reference Evangelias, Kuiroukidis and Throumoulopoulos2018); in this respect the condition (4.6) is trivially satisfied. Figure 6(a) shows that the condition
![]() ${\mathcal{A}}\geqslant 0$
in the absence of pressure anisotropy and flow,
${\mathcal{A}}\geqslant 0$
in the absence of pressure anisotropy and flow,
![]() $\unicode[STIX]{x1D70E}_{d}=M_{p_{0}}^{2}=0$
, is satisfied in a broad region including the outer domain and the two magnetic axes located on the left and right sides of the origin
$\unicode[STIX]{x1D70E}_{d}=M_{p_{0}}^{2}=0$
, is satisfied in a broad region including the outer domain and the two magnetic axes located on the left and right sides of the origin
![]() $(x=y=0)$
. In these regions, the term
$(x=y=0)$
. In these regions, the term
![]() $A_{2}$
, being stabilising, surpasses the destabilising term
$A_{2}$
, being stabilising, surpasses the destabilising term
![]() $A_{1}$
, as shown in figure 6(b) (while in this case the flow term
$A_{1}$
, as shown in figure 6(b) (while in this case the flow term
![]() $A_{3}$
vanishes). However, the condition is satisfied neither near the central magnetic axis, where
$A_{3}$
vanishes). However, the condition is satisfied neither near the central magnetic axis, where
![]() $J_{h}$
reverses and
$J_{h}$
reverses and
![]() $U$
is negative, nor in a small region located on the left side of the magnetic axis of the left lobe, in which
$U$
is negative, nor in a small region located on the left side of the magnetic axis of the left lobe, in which
![]() $V_{h}$
reverses; in this respect it should be noted that, since the condition is only sufficient, the white coloured regions in figure 6(a) and in the figures to follow, where
$V_{h}$
reverses; in this respect it should be noted that, since the condition is only sufficient, the white coloured regions in figure 6(a) and in the figures to follow, where
![]() ${\mathcal{A}}<0$
, do not necessarily imply instability. Thus, we will consider only regions in which the condition
${\mathcal{A}}<0$
, do not necessarily imply instability. Thus, we will consider only regions in which the condition
![]() ${\mathcal{A}}\geqslant 0$
is satisfied.
${\mathcal{A}}\geqslant 0$
is satisfied.

Figure 6. (a) For the static anisotropic helically symmetric equilibrium (
![]() $\unicode[STIX]{x1D70E}_{d}=M_{p_{0}}^{2}=0$
) the stability condition
$\unicode[STIX]{x1D70E}_{d}=M_{p_{0}}^{2}=0$
) the stability condition
![]() ${\mathcal{A}}\geqslant 0$
is satisfied in the orange coloured regions. (b) The term
${\mathcal{A}}\geqslant 0$
is satisfied in the orange coloured regions. (b) The term
![]() $A_{2}$
has a stabilising effect (red-dotted curve) which counteracts the destabilising one of
$A_{2}$
has a stabilising effect (red-dotted curve) which counteracts the destabilising one of
![]() $A_{1}$
(blue-dashed curve), so that the quantity
$A_{1}$
(blue-dashed curve), so that the quantity
![]() ${\mathcal{A}}=A_{1}+A_{2}$
, indicated by the black-straight curve, becomes positive in the aforementioned orange coloured regions.
${\mathcal{A}}=A_{1}+A_{2}$
, indicated by the black-straight curve, becomes positive in the aforementioned orange coloured regions.
The presence of pressure anisotropy does not affect the isotropic stability map of figure 6(a), as is clearly indicated in the profiles of figure 7. However, it affects the values of
![]() ${\mathcal{A}}$
. Specifically, in the regions where
${\mathcal{A}}$
. Specifically, in the regions where
![]() ${\mathcal{A}}\geqslant 0$
, for
${\mathcal{A}}\geqslant 0$
, for
![]() $P_{\Vert }>P_{\bot }$
(
$P_{\Vert }>P_{\bot }$
(
![]() $\unicode[STIX]{x1D70E}_{d}>0$
) the anisotropy has a stabilising impact, in the sense that the maximum values of
$\unicode[STIX]{x1D70E}_{d}>0$
) the anisotropy has a stabilising impact, in the sense that the maximum values of
![]() ${\mathcal{A}}$
become larger than the respective isotropic ones, and a destabilising effect for
${\mathcal{A}}$
become larger than the respective isotropic ones, and a destabilising effect for
![]() $\unicode[STIX]{x1D70E}_{d}<0$
occurs. These characteristics are illustrated in figure 7. In addition, it is found that the flow in terms of
$\unicode[STIX]{x1D70E}_{d}<0$
occurs. These characteristics are illustrated in figure 7. In addition, it is found that the flow in terms of
![]() $M_{p}^{2}$
has a peculiar effect on stability. Specifically, on the one hand, it results in shrinking of the orange coloured area located on the left-hand side of the first lobe, where the helicoidal velocity reverses, as can be seen in figure 8(a,b). This shrinking is connected with a destabilising effect of
$M_{p}^{2}$
has a peculiar effect on stability. Specifically, on the one hand, it results in shrinking of the orange coloured area located on the left-hand side of the first lobe, where the helicoidal velocity reverses, as can be seen in figure 8(a,b). This shrinking is connected with a destabilising effect of
![]() $M_{p_{0}}^{2}$
on both terms
$M_{p_{0}}^{2}$
on both terms
![]() $A_{1}$
and
$A_{1}$
and
![]() $A_{2}$
, as shown in figure 9(a,b). On the other hand, the flow has a stabilising effect, similar to that of
$A_{2}$
, as shown in figure 9(a,b). On the other hand, the flow has a stabilising effect, similar to that of
![]() $\unicode[STIX]{x1D70E}_{d}>0$
, because the respective maximum values of
$\unicode[STIX]{x1D70E}_{d}>0$
, because the respective maximum values of
![]() ${\mathcal{A}}$
get larger in this area as
${\mathcal{A}}$
get larger in this area as
![]() $M_{p}^{2}$
increases, as can be seen in figure 8(c). Also, the flow gives rise to a stabilising contribution via the term
$M_{p}^{2}$
increases, as can be seen in figure 8(c). Also, the flow gives rise to a stabilising contribution via the term
![]() $A_{3}$
. However, this contribution in the region of interest is an order of magnitude lower than the destabilising impact of
$A_{3}$
. However, this contribution in the region of interest is an order of magnitude lower than the destabilising impact of
![]() $M_{p}^{2}$
on
$M_{p}^{2}$
on
![]() $A_{1}$
and
$A_{1}$
and
![]() $A_{2}$
, as can be seen in figure 9(c). Because of the stronger impact of the pressure anisotropy on
$A_{2}$
, as can be seen in figure 9(c). Because of the stronger impact of the pressure anisotropy on
![]() ${\mathcal{A}}$
than the destabilising effect of the flow, the presence of both anisotropy and flow has an overall stabilising effect in terms of the region where the condition
${\mathcal{A}}$
than the destabilising effect of the flow, the presence of both anisotropy and flow has an overall stabilising effect in terms of the region where the condition
![]() ${\mathcal{A}}\geqslant 0$
is satisfied and the maximum values of
${\mathcal{A}}\geqslant 0$
is satisfied and the maximum values of
![]() ${\mathcal{A}}$
. This is shown in figure 10.
${\mathcal{A}}$
. This is shown in figure 10.

Figure 7. The impact of pressure anisotropy on the quantities (a)
![]() ${\mathcal{A}}$
, (b)
${\mathcal{A}}$
, (b)
![]() $A_{1}$
and (c)
$A_{1}$
and (c)
![]() $A_{2}$
in the absence of flow (
$A_{2}$
in the absence of flow (
![]() $M_{p_{0}}=0$
) for
$M_{p_{0}}=0$
) for
![]() $\unicode[STIX]{x1D70E}_{d}=0.2$
(blue-dashed curves) and
$\unicode[STIX]{x1D70E}_{d}=0.2$
(blue-dashed curves) and
![]() $\unicode[STIX]{x1D70E}_{d}=-0.2$
(red-dotted curve). For comparison, also given are the respective isotropic black continuous curves. In the regions where
$\unicode[STIX]{x1D70E}_{d}=-0.2$
(red-dotted curve). For comparison, also given are the respective isotropic black continuous curves. In the regions where
![]() ${\mathcal{A}}\geqslant 0$
, this impact is stabilising for
${\mathcal{A}}\geqslant 0$
, this impact is stabilising for
![]() $\unicode[STIX]{x1D70E}_{d}>0$
and destabilising for
$\unicode[STIX]{x1D70E}_{d}>0$
and destabilising for
![]() $\unicode[STIX]{x1D70E}_{d}<0$
.
$\unicode[STIX]{x1D70E}_{d}<0$
.

Figure 8. Impact of the flow through
![]() $M_{p_{0}}^{2}$
in the central orange coloured region where the stability condition
$M_{p_{0}}^{2}$
in the central orange coloured region where the stability condition
![]() ${\mathcal{A}}\geqslant 0$
is satisfied in comparison with the respective static isotropic equilibrium. The maximum used value of the parameter
${\mathcal{A}}\geqslant 0$
is satisfied in comparison with the respective static isotropic equilibrium. The maximum used value of the parameter
![]() $M_{p_{0}}$
, for which all the pressures remain positive, is 0.08.
$M_{p_{0}}$
, for which all the pressures remain positive, is 0.08.

Figure 9. The impact of the flow parameter
![]() $M_{p_{0}}^{2}$
on the terms (a)
$M_{p_{0}}^{2}$
on the terms (a)
![]() $A_{1}$
, (b)
$A_{1}$
, (b)
![]() $A_{2}$
and (c)
$A_{2}$
and (c)
![]() $A_{3}$
, for
$A_{3}$
, for
![]() $\unicode[STIX]{x1D70E}_{d}=0$
.
$\unicode[STIX]{x1D70E}_{d}=0$
.

Figure 10. The overall stabilising impact of pressure anisotropy in combination with flow on the stability of the constructed helically symmetric equilibria. The pertinent parametric values employed are as follows: (straight black curve)
![]() $\unicode[STIX]{x1D70E}_{d}=M_{p_{0}}^{2}=0$
, (blue dashed curve)
$\unicode[STIX]{x1D70E}_{d}=M_{p_{0}}^{2}=0$
, (blue dashed curve)
![]() $\unicode[STIX]{x1D70E}_{d}=0$
,
$\unicode[STIX]{x1D70E}_{d}=0$
,
![]() $M_{p_{0}}^{2}=0.07$
, (red dotted curve)
$M_{p_{0}}^{2}=0.07$
, (red dotted curve)
![]() $\unicode[STIX]{x1D70E}_{d}=0.07$
,
$\unicode[STIX]{x1D70E}_{d}=0.07$
,
![]() $M_{p_{0}}^{2}=0$
and (green dot-dashed curve)
$M_{p_{0}}^{2}=0$
and (green dot-dashed curve)
![]() $\unicode[STIX]{x1D70E}_{d}=M_{p_{0}}^{2}=0.07$
.
$\unicode[STIX]{x1D70E}_{d}=M_{p_{0}}^{2}=0.07$
.

Figure 11. The impact of the torsion of the magnetic axis and of the pitch on the linear stability of helically symmetric equilibria. Each pair of figures illustrates configurations that have same torsion, but different pitch values, as explained in the text.
Finally, as concerns the impact of the torsion,
![]() $\unicode[STIX]{x1D70F}$
, on the quantity
$\unicode[STIX]{x1D70F}$
, on the quantity
![]() ${\mathcal{A}}$
, for a specific helix, defined by the equations
${\mathcal{A}}$
, for a specific helix, defined by the equations
![]() $r=r_{c}=\text{const.}$
,
$r=r_{c}=\text{const.}$
,
![]() $u=u_{c}=\text{const.}$
(in helical coordinates), equation (6.8) implies that
$u=u_{c}=\text{const.}$
(in helical coordinates), equation (6.8) implies that
![]() $\unicode[STIX]{x1D70F}$
depends only on the parameter
$\unicode[STIX]{x1D70F}$
depends only on the parameter
![]() $\unicode[STIX]{x1D702}$
, which characterises the pitch of that helix. Inspection of (6.8) implies that
$\unicode[STIX]{x1D702}$
, which characterises the pitch of that helix. Inspection of (6.8) implies that
![]() $\unicode[STIX]{x1D70F}$
has an extremum for
$\unicode[STIX]{x1D70F}$
has an extremum for
![]() $\unicode[STIX]{x1D702}=r_{c}$
, corresponding to the maximum torsion,
$\unicode[STIX]{x1D702}=r_{c}$
, corresponding to the maximum torsion,
![]() $\unicode[STIX]{x1D70F}_{\max }=1/2r_{c}$
. For example, for the static, isotropic equilibrium of figure 1 the helical magnetic axis of the central lobe intersects the plane
$\unicode[STIX]{x1D70F}_{\max }=1/2r_{c}$
. For example, for the static, isotropic equilibrium of figure 1 the helical magnetic axis of the central lobe intersects the plane
![]() $z=0$
at the position
$z=0$
at the position
![]() $x_{c}=2.318,y_{c}=0$
, corresponding to
$x_{c}=2.318,y_{c}=0$
, corresponding to
![]() $r_{c}=2.318$
, and has maximum torsion,
$r_{c}=2.318$
, and has maximum torsion,
![]() $\unicode[STIX]{x1D70F}_{\max }=0.2157$
. Therefore, there can exist two different helically symmetric configurations with the same torsion but different pitches, one for
$\unicode[STIX]{x1D70F}_{\max }=0.2157$
. Therefore, there can exist two different helically symmetric configurations with the same torsion but different pitches, one for
![]() $\unicode[STIX]{x1D702}<r_{c}$
and the other
$\unicode[STIX]{x1D702}<r_{c}$
and the other
![]() $\unicode[STIX]{x1D702}>r_{c}$
. However, the same torsion does not imply that these configurations have necessarily the same stability properties. The region in which the condition
$\unicode[STIX]{x1D702}>r_{c}$
. However, the same torsion does not imply that these configurations have necessarily the same stability properties. The region in which the condition
![]() ${\mathcal{A}}\geqslant 0$
is satisfied for the equilibrium of figure 1 is shown in figure 6. We found the respective stability maps for the three pairs of equilibria, shown in figure 11. Each pair corresponds to the same torsion,
${\mathcal{A}}\geqslant 0$
is satisfied for the equilibrium of figure 1 is shown in figure 6. We found the respective stability maps for the three pairs of equilibria, shown in figure 11. Each pair corresponds to the same torsion,
![]() $\unicode[STIX]{x1D70F}<\unicode[STIX]{x1D70F}_{\max }$
but different pitch lengths,
$\unicode[STIX]{x1D70F}<\unicode[STIX]{x1D70F}_{\max }$
but different pitch lengths,
![]() $\unicode[STIX]{x1D702}<r_{c}$
and
$\unicode[STIX]{x1D702}<r_{c}$
and
![]() $\unicode[STIX]{x1D702}>r_{c}$
. Specifically, the torsion and pitch values we employed in connection with these equilibrium pairs are the following: (upper pair consisting of figure 11
a,b)
$\unicode[STIX]{x1D702}>r_{c}$
. Specifically, the torsion and pitch values we employed in connection with these equilibrium pairs are the following: (upper pair consisting of figure 11
a,b)
![]() $\unicode[STIX]{x1D70F}_{(a),(b)}=0.207,\unicode[STIX]{x1D702}_{(a)}=1.75,\unicode[STIX]{x1D702}_{(b)}=3.07$
, (middle pair consisting of the figure 11
c,d)
$\unicode[STIX]{x1D70F}_{(a),(b)}=0.207,\unicode[STIX]{x1D702}_{(a)}=1.75,\unicode[STIX]{x1D702}_{(b)}=3.07$
, (middle pair consisting of the figure 11
c,d)
![]() $\unicode[STIX]{x1D70F}_{(c),(d)}=0.157,\unicode[STIX]{x1D702}_{(c)}=1,\unicode[STIX]{x1D702}_{(d)}=5.37$
and (lower pair consisting of the figure 11
e,f)
$\unicode[STIX]{x1D70F}_{(c),(d)}=0.157,\unicode[STIX]{x1D702}_{(c)}=1,\unicode[STIX]{x1D702}_{(d)}=5.37$
and (lower pair consisting of the figure 11
e,f)
![]() $\unicode[STIX]{x1D70F}_{(e),(f)}=0.089,\unicode[STIX]{x1D702}_{(e)}=0.5,\unicode[STIX]{x1D702}_{(f)}=10.75$
. The stability maps indicate that the condition
$\unicode[STIX]{x1D70F}_{(e),(f)}=0.089,\unicode[STIX]{x1D702}_{(e)}=0.5,\unicode[STIX]{x1D702}_{(f)}=10.75$
. The stability maps indicate that the condition
![]() ${\mathcal{A}}\geqslant 0$
is satisfied in a wider region as the torsion decreases from its maximum value and for a given torsion
${\mathcal{A}}\geqslant 0$
is satisfied in a wider region as the torsion decreases from its maximum value and for a given torsion
![]() ${\mathcal{A}}$
it gets larger as the pitch length
${\mathcal{A}}$
it gets larger as the pitch length
![]() $\unicode[STIX]{x1D702}>r_{c}$
increases. Thus, we conclude that helical configurations with smaller torsion and bigger pitch lengths may have improved stability characteristics. This result is reasonable if one considers the limit of zero torsion and infinite pitch length in which a helically symmetric plasma column degenerates into an one-dimensional, cylindrical
$\unicode[STIX]{x1D702}>r_{c}$
increases. Thus, we conclude that helical configurations with smaller torsion and bigger pitch lengths may have improved stability characteristics. This result is reasonable if one considers the limit of zero torsion and infinite pitch length in which a helically symmetric plasma column degenerates into an one-dimensional, cylindrical
![]() $\unicode[STIX]{x1D703}$
-pinch. It is well known that such a configuration has favourable stability properties, since the safety factor approaches infinity. However, confinement in a
$\unicode[STIX]{x1D703}$
-pinch. It is well known that such a configuration has favourable stability properties, since the safety factor approaches infinity. However, confinement in a
![]() $\unicode[STIX]{x1D703}$
-pinch is not possible in the presence of toroidicity because the axial magnetic field becomes purely toroidal.
$\unicode[STIX]{x1D703}$
-pinch is not possible in the presence of toroidicity because the axial magnetic field becomes purely toroidal.
7 Conclusions
We have derived a sufficient condition for the linear stability of plasma equilibria for field-aligned incompressible flows in connection with plasmas of constant density and pressure anisotropy such that the pressure difference
![]() $P_{\Vert }^{\ast }-P_{\bot }^{\ast }$
be proportional to the magnetic pressure, by employing an energy principle. Specifically, we have shown that the linear stability of such equilibria is guaranteed when the functional of the perturbation potential energy relates to the sign of a function
$P_{\Vert }^{\ast }-P_{\bot }^{\ast }$
be proportional to the magnetic pressure, by employing an energy principle. Specifically, we have shown that the linear stability of such equilibria is guaranteed when the functional of the perturbation potential energy relates to the sign of a function
![]() ${\mathcal{A}}$
(equation (4.5)) which depends only on equilibrium quantities. According to that condition, any equilibrium is linearly stable to small three-dimensional perturbations whenever (i) the sum of the anisotropy function plus the Mach function of the equilibrium velocity colinear with the magnetic field is not larger than unity (equation (4.6)) and (ii)
${\mathcal{A}}$
(equation (4.5)) which depends only on equilibrium quantities. According to that condition, any equilibrium is linearly stable to small three-dimensional perturbations whenever (i) the sum of the anisotropy function plus the Mach function of the equilibrium velocity colinear with the magnetic field is not larger than unity (equation (4.6)) and (ii)
![]() ${\mathcal{A}}$
is non-negative (equation (4.7)). This condition generalises the sufficient condition derived in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007) for respective equilibria with isotropic pressure.
${\mathcal{A}}$
is non-negative (equation (4.7)). This condition generalises the sufficient condition derived in Throumoulopoulos & Tasso (Reference Throumoulopoulos and Tasso2007) for respective equilibria with isotropic pressure.
The aforementioned condition can be applied to any plasma steady state without geometrical restriction, that is, it can be employed for three-dimensional equilibria. The quantity
![]() ${\mathcal{A}}$
involved consists of three physically interpretable terms. The first of these terms, being always negative and therefore destabilising, may relate to current driven instabilities. The other two terms may make either a positive or negative contribution to
${\mathcal{A}}$
involved consists of three physically interpretable terms. The first of these terms, being always negative and therefore destabilising, may relate to current driven instabilities. The other two terms may make either a positive or negative contribution to
![]() ${\mathcal{A}}$
depending on the characteristics of the background equilibria. The second term relates to the magnetic shear, while the third term relates to the velocity shear and to the variation of the total pressure perpendicular to the magnetic surfaces; the latter term vanishes for static equilibria.
${\mathcal{A}}$
depending on the characteristics of the background equilibria. The second term relates to the magnetic shear, while the third term relates to the velocity shear and to the variation of the total pressure perpendicular to the magnetic surfaces; the latter term vanishes for static equilibria.
In addition, we have shown that, if a given equilibrium with field-aligned incompressible flows of constant mass density and constant pressure anisotropy function fulfils the aforementioned condition, and therefore is linearly stable, then all the families of equilibria obtained by the application of the symmetry transformations presented in Evangelias & Throumoulopoulos (Reference Evangelias and Throumoulopoulos2019) to the original equilibrium, are also linearly stable, provided that a parameter,
![]() $C$
, appearing in these transformations, is positive–definite.
$C$
, appearing in these transformations, is positive–definite.
At last, we applied the aforementioned sufficient condition to a special class of helically symmetric equilibrium solutions describing astrophysical jets in order to examine the impact of flow, pressure anisotropy as well as of the torsion and pitch of certain equilibrium configuration helices on stability. For this class of equilibria we have found that both the flow and the anisotropy can have noticeable impact on stability, which in different plasma regions can be either stabilising or destabilising; the impact of pressure anisotropy is stronger than that of the flow. Specifically, in the regions where the stability condition
![]() ${\mathcal{A}}\geqslant 0$
is satisfied, the combined effect of flow and anisotropy is stabilising when
${\mathcal{A}}\geqslant 0$
is satisfied, the combined effect of flow and anisotropy is stabilising when
![]() $P_{\Vert }>P_{\bot }$
. Finally, the results indicate that helically symmetric equilibrium configurations with smaller torsion and larger pitch length are favoured in terms of stability.
$P_{\Vert }>P_{\bot }$
. Finally, the results indicate that helically symmetric equilibrium configurations with smaller torsion and larger pitch length are favoured in terms of stability.
It is interesting to pursue potential extensions of the sufficient condition derived here to steady states with compressible flows or/and more physically relevant pressure anisotropy. This requires replacing incompressibility and the assumption of a constant pressure anisotropy function by alternative equations of state on the understanding that finding self-consistently more appropriate equations of state (or energy equations) associated with the pressure tensor elements
![]() $P_{\Vert }$
and
$P_{\Vert }$
and
![]() $P_{\bot }$
relates to the tough closure problem of a hybrid fluid-kinetic model, e.g. Snyder, Hammett & Dorland (Reference Snyder, Hammett and Dorland1997), Ramos (Reference Ramos2015).
$P_{\bot }$
relates to the tough closure problem of a hybrid fluid-kinetic model, e.g. Snyder, Hammett & Dorland (Reference Snyder, Hammett and Dorland1997), Ramos (Reference Ramos2015).
Acknowledgements
This study was performed within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 and 2019–2020 under grant agreement no. 633053 as well as the National Program for the Controlled Thermonuclear Fusion, Hellenic Republic. The views and opinions expressed herein do not necessarily reflect those of the European Commission. A.E. has in part been financially supported by the General Secretariat for Research and Technology (GSRT) and the Hellenic Foundation for Research and Innovation (HFRI).