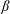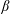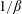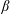Self-inhibiting thermal conduction in a high-$\unicode[STIX]{x1D6FD}$, whistler-unstable plasma

Abstract

A heat flux in a high-$\unicode[STIX]{x1D6FD}$ plasma with low collisionality triggers the whistler instability. Quasilinear theory predicts saturation of the instability in a marginal state characterized by a heat flux that is fully controlled by electron scattering off magnetic perturbations. This marginal heat flux does not depend on the temperature gradient and scales as $1/\unicode[STIX]{x1D6FD}$. We confirm this theoretical prediction by performing numerical particle-in-cell simulations of the instability. We further calculate the saturation level of magnetic perturbations and the electron scattering rate as functions of $\unicode[STIX]{x1D6FD}$ and the temperature gradient to identify the saturation mechanism as quasilinear. Suppression of the heat flux is caused by oblique whistlers with magnetic-energy density distributed over a wide range of propagation angles. This result can be applied to high-$\unicode[STIX]{x1D6FD}$ astrophysical plasmas, such as the intracluster medium, where thermal conduction at sharp temperature gradients along magnetic-field lines can be significantly suppressed. We provide a convenient expression for the amount of suppression of the heat flux relative to the classical Spitzer value as a function of the temperature gradient and $\unicode[STIX]{x1D6FD}$. For a turbulent plasma, the additional independent suppression by the mirror instability is capable of producing large total suppression factors (several tens in galaxy clusters) in regions with strong temperature gradients.

1 Introduction

Thermal conduction in a hot magnetized turbulent astrophysical plasma has been an active research topic since its potential role in the thermodynamics of galaxy clusters was appreciated (the so-called cooling flow problem; see, e.g. Ruszkowski & Begelman (2002), Zakamska & Narayan (2003), Voigt & Fabian (2004), Dennis & Chandran (2005)). It is often assumed to be significantly reduced relative to the unmagnetized Spitzer conductivity by magnetic fields, an assumption mainly based on observations of various temperature substructures in the intracluster medium (ICM): fluctuations on scales of the order of 100 kpc (Markevitch et al. 2003; Wang, Markevitch & Giacintucci 2016), sharp gradients at contact discontinuities (the so-called cold fronts; e.g. Ettori & Fabian (2000), Markevitch et al. (2000), Vikhlinin, Markevitch & Murray (2001), Markevitch & Vikhlinin (2007), Ichinohe et al. (2015)) and filamentary structures (e.g. in the Coma cluster; see Sanders et al. (2013)). However, the exact physics of such suppression remain to be understood. To some extent, the persistence of temperature fluctuations could be explained by the turbulent topology of magnetic-field lines that favours perpendicular orientation of temperature gradients and field lines (Komarov et al. 2014), while cold fronts likely survive for long times due to field-line draping, which has similar effect by stretching field lines along a cold front interface (Lyutikov 2006; Asai, Fukuda & Matsumoto 2007; Dursi & Pfrommer 2008).

It is in general more problematic to suppress parallel thermal conduction along magnetic-field lines. In order to inhibit parallel electron transport, small-scale magnetic fluctuations that presumably exist in the ICM due to various kinetic instabilities should be either in the form of transverse perturbations on electron Larmor scales (e.g. Levinson & Eichler 1992), or in the form of magnetic mirrors (i.e. longitudinal waves) on larger scales (e.g. Chandran & Cowley 1998). The latter may be provided on ion Larmor scales by the mirror instability, driven by anisotropy in the plasma temperature that is biased perpendicularly with respect to the local magnetic-field direction (Parker (1958), Hasegawa (1969); see also Kunz, Schekochihin & Stone (2014) and Rincon, Schekochihin & Cowley (2015) for the saturation mechanism). Suppression factors estimated for this case are rather modest, of the order of $1/3$ – $1/5$ of the Spitzer value (Komarov et al. 2016).

The transverse whistler instability seems to be the most promising candidate for scattering electrons at the scale of their Larmor radii. It has long been known that a heat flux in a weakly collisional magnetized plasma causes whistler instability under certain conditions and thus can, possibly, inhibit itself (Levinson & Eichler (1992); see also Ramani & Laval (1978) for the unmagnetized case). This problem presents significant theoretical interest, even outside of the context of galaxy clusters. Levinson & Eichler (1992) first described the linear heat-flux-induced whistler instability and estimated the suppression of thermal conduction by assuming that saturation of the instability is controlled by nonlinear mode coupling. In their work, they employed the simple isotropic Krook operator in order to describe electron scattering off whistler perturbations. Pistinner & Eichler (1998) (hereafter PE98) questioned the validity of this assumption and demonstrated that in the framework of quasilinear theory (QLT), the marginal electron distribution function in fact generates oblique whistlers able to scatter heat-carrying electrons efficiently. Both Levinson & Eichler (1992) and PE98 stressed the fact that strictly parallel whistler modes do not interact with heat-carrying electrons intensively, because the Doppler-shifted circular rotation of the E-vector of these modes in the frame moving with the electrons along the mean magnetic field is opposite to the gyration of the electrons. The elliptical polarization of oblique modes, on the other hand, alleviates this problem and enables resonant interaction with the heat-carrying particles. The resulting heat flux in PE98 turns out to be independent of the temperature gradient and scales as the inverse electron plasma $\unicode[STIX]{x1D6FD}_{e}$ .

In this work, we study the heat-flux-induced whistler instability with the aid of particle-in-cell numerical simulations. By performing runs with different values of $\unicode[STIX]{x1D6FD}_{e}$ and temperature gradients, we arrive at qualitatively the same conclusion as PE98: the saturated whistler modes are oblique and, therefore, successfully inhibit the electron heat flux, restricting it to the $\unicode[STIX]{x1D6FD}_{e}^{-1}$ scaling regardless of the magnitude of the temperature gradient. We also show that the saturated magnetic-field energy, as well as the pitch-angle scattering rate follow the same functional form as predicted by QLT.

During the final stage of preparation of this paper, Roberg-Clark et al. (2018) published a very similar numerical result (see also Roberg-Clark et al. (2016) for their previous work on this subject). Our work can be considered as an independent confirmation of their main result, namely, the fact that the heat flux controlled by the instability scales as $\unicode[STIX]{x1D6FD}_{e}^{-1}$ . However, we propose a rather different physical approach to the interpretation of this result, based on quasilinear saturation near marginal stability. In addition, we discuss some of the aspects of the instability in more detail, e.g. the structure of the electron distribution function in the marginal state and the scaling of the pitch-angle scattering rate and saturation level of magnetic perturbations with $\unicode[STIX]{x1D6FD}_{e}$ and the temperature gradient. We also provide a convenient expression for the suppression factor of the heat flux applicable to clusters of galaxies. This model could be easily incorporated into hydro- and magnetohydrodynamic numerical simulations.

The rest of this paper is organized as follows. In § 2, we present a qualitative explanation of the physics behind the heat-flux suppression by whistler turbulence based on the marginality criterion. We then turn to numerical results (§ 3) to support this model. We proceed with discussion of the relevance of our results to galaxy clusters and the limitations of our model in § 4. We summarize our findings in § 5.

2 Theoretical considerations

2.1 General remarks

Let us assume that due to a certain anisotropy of the electron distribution function in a weakly collisional magnetized plasma, it becomes unstable and triggers electromagnetic modes propagating in some direction with phase velocities $\unicode[STIX]{x1D714}/k$ , where $\unicode[STIX]{x1D714}$ is the wave frequency and $k$ is the wavenumber. We assume also that the electrons are fast compared to the wave (as tends to be the case for for low-frequency modes in a hot plasma), so the electron Landau resonance is ineffective and wave–particle interactions mostly happen via gyroresonances $k_{\Vert }v_{\Vert }=\pm \unicode[STIX]{x1D6FA}_{e}$ , where $k_{\Vert }$ is the parallel (to the mean magnetic field) wavenumber, $v_{\Vert }$ the parallel electron velocity, and $\unicode[STIX]{x1D6FA}_{e}$ the electron Larmor frequency. Let the unstable modes have random phases and a sufficiently broad spectrum, viz., $\unicode[STIX]{x0394}k/k\sim 1$ . This allows electrons within a wide range of parallel velocities to resonate with different uncorrelated wave modes. For an electromagnetic wave, the perpendicular electric field $\unicode[STIX]{x1D6FF}E_{\bot }^{\prime }$ in the reference frame moving at the parallel phase velocity of the wave is zero:

(2.1) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}E_{\bot }^{\prime }=\unicode[STIX]{x1D6FF}E_{\bot }-\unicode[STIX]{x1D714}/(k_{\Vert }c)\unicode[STIX]{x1D6FF}B_{\bot }=\unicode[STIX]{x1D6FF}E_{\bot }-[\unicode[STIX]{x1D714}/(k_{\Vert }c)](c/\unicode[STIX]{x1D714})k_{\Vert }\unicode[STIX]{x1D6FF}E_{\bot }=0, & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D6FF}B_{\bot }$ and $\unicode[STIX]{x1D6FF}E_{\bot }$ are the perpendicular magnetic and electric fields of the wave in the laboratory frame, and $c$ is the speed of light. The parallel electric field (unaffected by the change of the reference frame) can be safely assumed unimportant because it only interacts with electrons via Landau resonance, but because the wave is slow compared to the electron thermal speed, such interaction is weak, and there is no secular change in a particle’s energy ¹ . Resonant particles, which are the ones that mostly contribute to the initial anisotropy (the instability drains free energy from the anisotropy by resonant wave–particle interactions), are scattered elastically by magnetic perturbations in the moving frame. Eventually, this leads to isotropization of their distribution function in the ‘wave frame’ and quenching of the instability. Thus, an excess of particles at parallel momenta in the direction of the wave propagation larger than of the order of $m_{e}\unicode[STIX]{x1D714}/k_{\Vert }$ in the laboratory frame are not allowed.

Let us assume for illustrative purposes that the electrons have a non-zero mean momentum in the direction of the wave, causing an asymmetry in the electron distribution function. We may define the anisotropy of such distribution simply as $\unicode[STIX]{x1D716}=\langle p_{\Vert }\rangle /p_{\text{th}}$ , where $\langle p_{\Vert }\rangle$ is the mean parallel momentum and $p_{\text{th}}=(2m_{e}T)^{1/2}$ the electron thermal momentum (we use energy units of temperature everywhere). Then, the instability limits such anisotropy by $\unicode[STIX]{x1D716}_{\text{max}}\sim \unicode[STIX]{x1D714}/k_{\Vert }v_{\text{th}}$ , where $v_{\text{th}}$ is the electron thermal velocity. A parallel heat flux is, in fact, characterized by a similar perturbation of the distribution function ² at parallel velocities $v_{\Vert }\sim \pm v_{\text{th}}$ . We can approximately estimate the heat flux as

(2.2) $$\begin{eqnarray}\displaystyle q_{\Vert }\sim m_{e}nv_{\text{th}}^{2}\langle v_{\Vert }\rangle \sim \unicode[STIX]{x1D716}m_{e}nv_{\text{th}}^{3}, & & \displaystyle\end{eqnarray}$$

where $n$ is the electron density. For the heat-carrying particles, the resonant scale is simply the electron Larmor radius $\unicode[STIX]{x1D70C}_{e}=v_{\text{th}}/\unicode[STIX]{x1D6FA}_{e}$ , which follows from the gyroresonance condition $k_{\Vert }v_{\Vert }=\pm \unicode[STIX]{x1D6FA}_{e}$ . The frequency of whistler waves at this scale is

(2.3) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}\sim (\unicode[STIX]{x1D6FA}_{e}/\unicode[STIX]{x1D714}_{\text{p}}^{2})k^{2}c^{2}\sim (k\unicode[STIX]{x1D70C}_{e})^{2}\unicode[STIX]{x1D6FA}_{e}/\unicode[STIX]{x1D6FD}_{e}\sim \unicode[STIX]{x1D6FA}_{e}/\unicode[STIX]{x1D6FD}_{e}. & & \displaystyle\end{eqnarray}$$

Thus, the whistler phase velocity is $v_{\text{th}}/\unicode[STIX]{x1D6FD}_{e}$ , and, immediately, if whistler turbulence saturates by electron pitch-angle scattering, it limits the maximum anisotropy to ${\sim}1/\unicode[STIX]{x1D6FD}_{e}$ . Equivalently, the marginal heat flux should be

(2.4) $$\begin{eqnarray}\displaystyle q_{\Vert }\sim \unicode[STIX]{x1D6FD}_{e}^{-1}m_{e}nv_{\text{th}}^{3}, & & \displaystyle\end{eqnarray}$$

provided that such flux turns out to be smaller than the initial heat flux with no instability. Already from these simplified arguments, one gets a heat flux that is fully controlled by the plasma $\unicode[STIX]{x1D6FD}$ and is independent of the imposed temperature gradient. This is exactly the conclusion made by PE98 via a more rigorous quasilinear derivation.

2.2 Whistler instability

It is most convenient to establish the connection between the electron distribution function and the growth rate with the help of basic semi-classical concepts (Melrose 1980). This method is physically equivalent to the usual derivation based on the Landau–Laplace procedure. We prefer this derivation because it provides a quick shortcut to the expression for the growth rate in a form that allows one to study marginal distribution functions without knowing the complicated details of the dispersion relation in the general case of oblique wave propagation. We also believe it is clearer for a reader less familiar with plasma kinetics, because it does not introduce from the start the dispersion relation, which is often hard to interpret physically.

Let an electron with momentum $\boldsymbol{p}$ gyrating in a magnetic field emit a photon with momentum $\hbar \boldsymbol{k}$ . The change in the electron’s parallel momentum is

(2.5) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}p_{\Vert }=-\hbar k_{\Vert }. & & \displaystyle\end{eqnarray}$$

Conservation of energy implies

(2.6) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}\frac{p_{\Vert }^{2}}{2m_{e}}+\unicode[STIX]{x0394}\frac{p_{\bot }^{2}}{2m_{e}}+\hbar \unicode[STIX]{x1D714}=0. & & \displaystyle\end{eqnarray}$$

The perpendicular kinetic energy of an electron in a magnetic field is quantized as $E_{\bot }=j\hbar \unicode[STIX]{x1D6FA}_{e}$ , where $j$ is a non-negative integer (we can ignore the electron’s spin and ground-state energy here as we are interested in the classical limit $j\gg 1$ ). Then the change in the perpendicular momentum of the electron is

(2.7) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}p_{\bot }=-s\hbar \unicode[STIX]{x1D6FA}_{e}/v_{\bot }, & & \displaystyle\end{eqnarray}$$

where $s$ is an integer. From (2.6), using (2.5), we get

(2.8) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}-k_{\Vert }v_{\Vert }=s\unicode[STIX]{x1D6FA}_{e}. & & \displaystyle\end{eqnarray}$$

This is just the normal resonance condition, which is in fact the statement of energy conservation.

The number of emitted photons with wave vector $\boldsymbol{k}$ per unit time between two electron states with momenta $\boldsymbol{p}$ and $\boldsymbol{p}-\hbar \boldsymbol{k}$ is set by the difference between the rates of stimulated emission and stimulated absorption. The former should be proportional to the electron distribution function at the higher momentum $\boldsymbol{p}$ , $f(\,\boldsymbol{p})$ , and the latter to $f(\,\boldsymbol{p}-\hbar \boldsymbol{k})$ . Assuming that the emitted/absorbed momentum is small and using (2.5) and (2.7), we get

(2.9) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}f(\,\boldsymbol{p},\boldsymbol{k})=f(\,\boldsymbol{p})-f(\,\boldsymbol{p}-\hbar \boldsymbol{k})=-\unicode[STIX]{x0394}p_{\bot }\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}p_{\bot }}-\unicode[STIX]{x0394}p_{\Vert }\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}p_{\Vert }}=\hbar \left(\frac{s\unicode[STIX]{x1D6FA}_{e}}{v_{\bot }}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}p_{\bot }}+k_{\Vert }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}p_{\Vert }}\right)f(\,\boldsymbol{p}). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

Now we can obtain the rate of energy transfer from the electrons to the wave by integrating over electron momenta:

(2.10) $$\begin{eqnarray}\displaystyle \frac{\text{d}{\mathcal{E}}(\boldsymbol{k})}{\text{d}t}=\int \text{d}^{3}\boldsymbol{p}\,w(\,\boldsymbol{p},\boldsymbol{k})\unicode[STIX]{x0394}f(\,\boldsymbol{p},\boldsymbol{k}){\mathcal{E}}(\boldsymbol{k}), & & \displaystyle\end{eqnarray}$$

where ${\mathcal{E}}(\boldsymbol{k})$ is the density of energy contained in the wave, $w(\,\boldsymbol{p},\boldsymbol{k})={\mathcal{W}}(\,\boldsymbol{p},\boldsymbol{k})\unicode[STIX]{x1D6FF}(p_{\Vert }-p_{\Vert r})$ is the probability of stimulated emission/absorption of a photon with wave vector $\boldsymbol{k}$ by an electron with momentum $\boldsymbol{p}$ per unit of time, and $p_{\Vert r}=m_{e}(\unicode[STIX]{x1D714}-s\unicode[STIX]{x1D6FA}_{e})/k_{\Vert }$ is the resonant parallel momentum. The non-negative function ${\mathcal{W}}(\,\boldsymbol{p},\boldsymbol{k})$ contains all the information about the dispersion relation of the particular emitted mode. The wave energy growth rate $\unicode[STIX]{x1D6FE}_{s}(\boldsymbol{k})$ is then

(2.11) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{s}(\boldsymbol{k})=\int \text{d}^{3}\boldsymbol{p}\,w(\,\boldsymbol{p},\boldsymbol{k})\unicode[STIX]{x0394}f(\,\boldsymbol{p},\boldsymbol{k}). & & \displaystyle\end{eqnarray}$$

Here and in what follows, the subscript $s$ indicates that the growth rate $\unicode[STIX]{x1D6FE}_{s}$ is given for a single- $s$ resonance (2.8), while the total growth rate is an infinite sum over $s$ . Using (2.9), we finally arrive at a general expression for the growth rate of an arbitrary electromagnetic mode in the form

(2.12) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{s}(\boldsymbol{k})=\int \text{d}^{3}\boldsymbol{p}\,\unicode[STIX]{x1D6FF}(p_{\Vert }-p_{\Vert r}){\mathcal{W}}(\,\boldsymbol{p},\boldsymbol{k})\hbar \left(\frac{s\unicode[STIX]{x1D6FA}_{e}}{v_{\bot }}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}p_{\bot }}+k_{\Vert }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}p_{\Vert }}\right)f(\,\boldsymbol{p}). & & \displaystyle\end{eqnarray}$$

Expression (2.12) is convenient in the sense that it is valid for waves propagating at arbitrary angles, and it allows one to link the sign of the growth rate to properties of the distribution function without knowing the complicated dispersion relation for the general case of oblique propagation. The sign of $\unicode[STIX]{x1D6FE}_{s}(\boldsymbol{k})$ is determined by function

(2.13) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{s}(p_{\bot },\boldsymbol{k})=\left(\frac{s\unicode[STIX]{x1D6FA}_{e}}{v_{\bot }}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}p_{\bot }}+k_{\Vert }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}p_{\Vert }}\right)f(\,\boldsymbol{p})|_{p_{\Vert }=p_{\Vert r}}. & & \displaystyle\end{eqnarray}$$

Switching to velocity derivatives and using the resonance condition (2.8), we get

(2.14) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{s}(v_{\bot },\boldsymbol{k})\propto \frac{k_{\Vert }}{|k_{\Vert }|}\left[-\left(v_{\Vert }-\frac{\unicode[STIX]{x1D714}}{k_{\Vert }}\right)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v_{\bot }}+v_{\bot }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v_{\Vert }}\right]f(\boldsymbol{v})|_{v_{\Vert }=v_{\Vert r}}. & & \displaystyle\end{eqnarray}$$

Note that the sum of the partial derivatives in (2.14) is a derivative taken along semicircles $(v_{\Vert }-\unicode[STIX]{x1D714}/k_{\Vert })^{2}+v_{\bot }^{2}=\text{const}$ . This represents the fact that electron energy is conserved in the frame moving with the parallel phase velocity of the wave (because the perpendicular electric field is zero there). Equation (2.14) can be cast in a compact form:

(2.15) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{s}(v_{\bot },\boldsymbol{k})\propto \frac{k_{\Vert }}{|k_{\Vert }|}\hat{\boldsymbol{l}}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}\boldsymbol{v}}\bigg|_{v_{\Vert }=v_{\Vert r}}, & & \displaystyle\end{eqnarray}$$

where $\hat{\boldsymbol{l}}=(\sin \unicode[STIX]{x1D719},-\text{cos}\,\unicode[STIX]{x1D719})$ is a unit vector pointing clockwise along the contours of constant energy in the wave frame, and $\unicode[STIX]{x1D719}$ is the polar angle in coordinates $(v_{\Vert }-\unicode[STIX]{x1D714}/k_{\Vert },v_{\bot })$ . Let us choose $k_{\Vert }>0$ without loss of generality. We see that instability occurs when the distribution function near the resonant parallel momenta increases in the clockwise direction along the equi-energy contours in the wave frame. For the resonance at $v_{\Vert }\approx -\unicode[STIX]{x1D6FA}_{e}/k_{\Vert }$ , a parallel momentum deficiency (or, equivalently, a surplus of particles with high $v_{\bot }$ ) is needed for the instability to occur, while at $v_{\Vert }\approx \unicode[STIX]{x1D6FA}_{e}/k_{\Vert }$ one needs an excess of parallel momentum (see figure 1 for an illustration). The case of $k_{\Vert }<0$ is analogous and described by the oriented contours of constant energy in figure 1 mirror reflected with respect to the $y$ -axis, i.e. the direction of positive wave growth changes to counterclockwise.

2.3 Marginal heat flux

Provided that the spectrum of excited modes is sufficiently broad ( $\unicode[STIX]{x0394}k_{\Vert }/k_{\Vert }\sim 1$ ), particles in a wide range of parallel velocities are scattered by magnetic perturbations, and their isotropization in the wave frame leads to marginal stability.

Figure 1. An illustration of the mechanism of the whistler instability and marginality of the electron distribution function. The coloured contours show Maxwell’s distribution on the left and the anisotropic perturbation associated with a heat flux on the right (the heat flux is along the $v_{\Vert }$ axis). The left and right dashed vertical lines in (a,b) indicate the positions of the gyroresonances, while the central dashed lines correspond to the parallel phase velocity of a whistler. The solid circles demonstrate the contours of constant energy in the frame moving with the parallel phase velocity of the wave. We choose to use $v_{z}$ instead of $v_{\bot }=(v_{y}^{2}+v_{z}^{2})^{1/2}$ for the vertical axis solely because it is allowed to be negative, which makes for a more natural visual representation of the distribution function. The instability grows when the distribution function near the resonances increases in the clockwise direction (for $v_{z}>0$ ) along the solid circles, as for the heat-flux perturbation on the right. Driving by the anisotropy is balanced by cyclotron damping on the bulk of isotropic particles (a). If the wave spectrum is broad enough ( $\unicode[STIX]{x0394}k_{\Vert }/k_{\Vert }\sim 1$ ), electrons are scattered within a wide range of parallel velocities, and marginality is reached when electrons become isotropic in the wave frame. Both negative and positive resonances are only enabled for oblique whistlers, as described in the text.

A parallel heat flux introduces an asymmetry in the electron distribution function, and the perturbed distribution can be expanded in small parameter $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D706}_{\text{mfp}}/L_{T}$ , where $\unicode[STIX]{x1D706}_{\text{mfp}}$ is the electron mean free path (either classical Spitzer or one associated with scattering off magnetic fluctuations) and $L_{T}$ is the scale length of the temperature gradient. The heat flux is

(2.16) $$\begin{eqnarray}\displaystyle q_{\Vert }\sim n\unicode[STIX]{x1D706}_{\text{mfp}}v_{\text{th}}\unicode[STIX]{x1D735}T\sim \unicode[STIX]{x1D716}nv_{\text{th}}T\propto \unicode[STIX]{x1D716}, & & \displaystyle\end{eqnarray}$$

where $n$ and $T$ are the electron density and temperature.

The electron distribution function is

(2.17) $$\begin{eqnarray}\displaystyle f(v,\unicode[STIX]{x1D709})=f_{0}(v)+\unicode[STIX]{x1D716}f_{1}(v,\unicode[STIX]{x1D709}), & & \displaystyle\end{eqnarray}$$

where $f_{0}(v)$ is the unperturbed isotropic Maxwell distribution and $f_{1}(v,\unicode[STIX]{x1D709})$ is an anisotropic perturbation that depends on $\unicode[STIX]{x1D709}$ , the cosine of the electron pitch angle. Both of the components are shown in figure 1 with equi-energy contours superimposed. For $f_{1}$ we use the shape of distortion that arises from the Knudsen expansion of the Boltzmann equation with the simplest Krook operator describing isotropic collisions (e.g. Levinson & Eichler 1992):

(2.18) $$\begin{eqnarray}\displaystyle f_{1}(v,\unicode[STIX]{x1D709})=\frac{\unicode[STIX]{x1D709}v}{2v_{\text{th}}}\left(\frac{v^{2}}{v_{\text{th}}^{2}}-5\right)f_{0}(v). & & \displaystyle\end{eqnarray}$$

This is done only for illustrative purposes, and in fact any perturbation by a heat flux, with the proviso that no electron current is produced, can be used instead. All such perturbations will have similar features, namely, an excess of parallel momentum in the direction of the heat flux at ${\sim}2v_{\text{th}}$ , its deficiency in the opposite direction, and a backflow of colder particles (the central dipole-shaped pattern in figure 1 b) to cancel the electron current. Figure 1 demonstrates that the Maxwellian part (a) absorbs energy from the wave (see (2.15)), while the anisotropy associated with the heat flux provides the free-energy source driving the instability. To make it clearer, we can estimate the parallel phase speed of resonant whistlers in (2.14). By taking $|v_{\Vert r}|\sim v_{\text{th}}$ (see the resonances in figure 1) and, therefore, $k_{\Vert }\sim \unicode[STIX]{x1D70C}_{e}^{-1}$ , we get

(2.19) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}/k_{\Vert }=k_{\Vert }c^{2}\unicode[STIX]{x1D6FA}_{e}/\unicode[STIX]{x1D714}_{p}^{2}\sim v_{\text{th}}/\unicode[STIX]{x1D6FD}_{e}. & & \displaystyle\end{eqnarray}$$

Let us also change variables in (2.14) to $(v,\unicode[STIX]{x1D709})$ and use the fact that $\unicode[STIX]{x1D714}\ll |k_{\Vert }v_{\Vert }|$ . This leads to

(2.20) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{s}(\boldsymbol{v},\boldsymbol{k})\propto \left(\frac{v_{\text{th}}}{\unicode[STIX]{x1D6FD}_{e}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}v}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\right)f(v,\unicode[STIX]{x1D709})|_{v_{\Vert }=v_{\Vert r}}\approx \left(\frac{v_{\text{th}}}{\unicode[STIX]{x1D6FD}_{e}}\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v}+\unicode[STIX]{x1D716}\frac{\unicode[STIX]{x2202}f_{1}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\right)_{v_{\Vert }=v_{\Vert r}}. & & \displaystyle\end{eqnarray}$$

It is manifest now that the growth rate consists of two terms: the damping term that describes suppression of waves by the bulk of isotropic particles (electron cyclotron damping), and the driving term proportional to the anisotropic distortion of the distribution function, i.e. to the heat flux. Note that (2.20) is written for $k_{\Vert }>0$ ; for $k_{\Vert }<0$ there is no instability because $\unicode[STIX]{x1D6E4}_{s}$ reverses its sign in (2.15), and the driving term in (2.20) becomes negative, while the damping term proportional to the phase speed remains negative because the phase speed also changes its sign.

By estimating $\unicode[STIX]{x2202}f_{0}/\unicode[STIX]{x2202}v\sim -f_{0}/v_{\text{th}}$ , $\unicode[STIX]{x2202}f_{1}/\unicode[STIX]{x2202}\unicode[STIX]{x1D709}\sim f_{1}$ , $f_{1}\sim f_{0}$ and demanding marginal stability $\unicode[STIX]{x1D6FE}=0$ , we get

(2.21) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{e}\sim 1. & & \displaystyle\end{eqnarray}$$

Thus, the marginal heat flux is

(2.22) $$\begin{eqnarray}\displaystyle q_{\Vert }^{\text{m}}\sim \unicode[STIX]{x1D6FD}_{e}^{-1}nv_{\text{th}}T. & & \displaystyle\end{eqnarray}$$

We have achieved the result anticipated in (2.4): the marginal heat flux is limited by the value of the phase speed of resonant whistlers and, therefore, is fully controlled by the electron plasma $\unicode[STIX]{x1D6FD}_{e}$ .

It is helpful for further discussion to go back and estimate the order of magnitude of the driving and damping terms, as we have so far been interested only in the sign of the growth rate. Ignoring the angular dependence, ${\mathcal{W}}(\,\boldsymbol{p},\boldsymbol{k})$ in (2.12) can be estimated as ${\mathcal{W}}(\boldsymbol{v},\boldsymbol{k})\sim m_{e}^{2}v^{3}/\hbar n$ (see Melrose 1980, equation (7.46)). Then, using (2.12), (2.13), (2.20) and the resonance condition $k_{\Vert }\sim \unicode[STIX]{x1D70C}_{e}^{-1}$ , we get

(2.23) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{\text{grow}}/\unicode[STIX]{x1D6FA}_{e} & {\sim} & \displaystyle \unicode[STIX]{x1D716},\end{eqnarray}$$

(2.24) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{\text{damp}}/\unicode[STIX]{x1D6FA}_{e} & {\sim} & \displaystyle 1/\unicode[STIX]{x1D6FD}_{e}.\end{eqnarray}$$

2.4 Resonant wave–particle interaction: need for oblique whistlers

So far we have completely ignored the details of the resonant interaction between the heat-carrying electrons and whistler waves. Namely, we have simply considered that both gyroresonances are active, and particles with both negative and positive parallel velocities are scattered by the magnetic perturbations. However, because the whistler wave is an electromagnetic wave modified by gyrating electrons, it is right-hand polarized. Whistlers that propagate along the mean magnetic field have a right-hand circular polarization. This means that they strongly interact only with electrons moving opposite to the wave (and the field) because those are the ones that co-rotate with the electric-field vector of the wave in the frame moving with the parallel electron velocity $v_{\Vert }$ . The corresponding resonance condition for parallel propagation is $\unicode[STIX]{x1D714}-k_{\Vert }v_{\Vert }\approx -k_{\Vert }v_{\Vert }=\unicode[STIX]{x1D6FA}_{e}$ , where the positive sign before $\unicode[STIX]{x1D6FA}_{e}$ is fixed by the right-hand polarization of the wave. This is the left gyroresonance in figure 1. Analysis of the linear whistler growth rate done by substitution of the whistler dispersion properties into the function ${\mathcal{W}}(\,\boldsymbol{p},\boldsymbol{k})$ in (2.12) and using the Knudsen expansion of the electron distribution function in the presence of a small collisional heat flux (set by isotropic Coulomb collisions) is a difficult task for whistlers with arbitrary propagation angles. It is drastically simplified for the case of near-parallel propagation, and predicts that the maximum growth rate is reached for strictly parallel whistlers that resonate, as we have noted, with electrons moving opposite to the heat flux (see PE98). Such whistlers are not expected to scatter the heat-carrying electrons.

From figure 1(b), it can be seen that it is regions of high $v_{\bot }$ and negative $v_{\Vert }$ that drive the parallel whistlers. Scattering off the parallel modes modifies the electron distribution, and it evolves to a new current-free distribution, different from the initial state obtained from the Knudsen expansion. Because such scattering is not isotropic, the dependence of the new marginally stable distribution function on the cosine of the electron pitch angle $\unicode[STIX]{x1D709}$ no longer has to be in the simple dipole form $f_{1}=\unicode[STIX]{x1D709}\unicode[STIX]{x1D719}_{1}(v)$ as in the Knudsen expansion (see (2.18) and figure 1). The new state may be characterized by more depletion of the anisotropy at negative $v_{\Vert }\sim -2v_{\text{th}}$ compared with the one at $v_{\Vert }\sim 2v_{\text{th}}$ associated with the heat flux. We will further show in § 3.2.2 that such state is indeed seen in our numerical simulations. In this state, the maximum growth rate can be achieved for oblique whistler propagation instead. Oblique modes, in contrast with parallel, are right-hand elliptically polarized, which can be represented as a combination of right- and left-hand circularly polarized waves. Thus, both positive and negative resonances, $k_{\Vert }v_{\Vert }=\pm \unicode[STIX]{x1D6FA}_{e}$ , become active (see figure 1), and efficient scattering of the heat-carrying particles is possible. PE98 used quasilinear equations to predict that the final marginal state is indeed characterized by whistlers propagating at a large angle to the mean magnetic field. However, their result is not fully self-consistent because they still relied on the approximation of the whistler dispersion relation for near-parallel propagation, while the resulting angle of propagation was found to be large. In the face of significant analytical complexity of even the quasilinear treatment of the instability, numerical simulations are vital in order to test the expectation that oblique whistlers will dominate the marginal state.

2.5 Saturated magnetic field

Let us assume that electron orbits are only weakly perturbed by the unstable whistlers, nonlinear effects can be neglected due to the smallness of the saturated magnetic fluctuations, and saturation is quasilinear (an assumption that will be confirmed in § 3.2.4). The scattering rate $\unicode[STIX]{x1D708}_{\text{scatt}}$ of resonant electrons can be expressed via $\unicode[STIX]{x1D716}$ (see the beginning of § 2.3) as

(2.25) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{\text{scatt}}=\frac{v_{\text{th}}}{\unicode[STIX]{x1D706}_{\text{mfp}}}=\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FA}_{e}\frac{\unicode[STIX]{x1D70C}_{e}}{L_{T}}, & & \displaystyle\end{eqnarray}$$

or, using the marginality condition (2.21),

(2.26) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D708}_{\text{scatt}}}{\unicode[STIX]{x1D6FA}_{e}}\sim \unicode[STIX]{x1D6FD}_{e}\frac{\unicode[STIX]{x1D70C}_{e}}{L_{T}}. & & \displaystyle\end{eqnarray}$$

Given that the resonant magnetic perturbations arise at the electron Larmor scale, both gyroresonances are available (assuming oblique propagation), and the whistler spectrum is sufficiently broad to scatter particles isotropically, we can estimate the effective pitch-angle scattering rate from Bohm diffusion:

(2.27) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D708}_{\text{scatt}}}{\unicode[STIX]{x1D6FA}_{e}}\sim \frac{\unicode[STIX]{x1D6FF}B^{2}}{B_{0}^{2}}, & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D6FF}B$ is the saturated magnitude of the magnetic perturbations at the resonant parallel wavelength $k_{\Vert r}=\unicode[STIX]{x1D6FA}_{e}/\unicode[STIX]{x1D709}v$ and $B_{0}$ the mean magnetic field. This allows one to obtain the saturated magnetic field:

(2.28) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}B^{2}}{B_{0}^{2}}\sim \unicode[STIX]{x1D6FD}_{e}\frac{\unicode[STIX]{x1D70C}_{e}}{L_{T}}. & & \displaystyle\end{eqnarray}$$

Note that this quasilinear saturation level is extremely low for astrophysical plasmas. For galaxy clusters, $\unicode[STIX]{x1D70C}_{e}/L_{T}\lesssim 10^{-13}$ at temperature $T=10~\text{KeV}$ , magnetic field $B_{0}=1~\unicode[STIX]{x03BC}\text{G}$ and $L_{T}\gtrsim 10~\text{kpc}$ , while $\unicode[STIX]{x1D6FD}_{e}\sim 100$ . The resulting saturation level then is $\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}\sim 10^{-11}$ .

3 Numerical simulations

By performing numerical simulations with different $\unicode[STIX]{x1D6FD}_{e}$ and $\unicode[STIX]{x1D70C}_{e}/L_{T}$ , we will now check the validity of our assumptions and qualitative results: the oblique propagation of whistlers, the expressions for the marginal heat flux (2.22), effective pitch-angle scattering rate (2.26) and the saturated level of magnetic fluctuations (2.28), all as functions of $\unicode[STIX]{x1D6FD}_{e}$ and $\unicode[STIX]{x1D70C}_{e}/L_{T}$ .

3.1 Numerical set-up

We use the relativistic electromagnetic particle-in-cell code TRISTAN (Buneman 1993, Spitkovsky 2005). Our simulation domain is an elongated two-dimensional (2-D) grid of size $N_{x}\times N_{y}=2560\times 512$ with the number of particles per cell varying from 200 to 500 depending on the run to obtain convergence and an acceptable signal-to-noise ratio. The simulation is 2.5-dimensional, meaning that particle velocities are three dimensions. The ions are motionless and form a charge-neutralizing background (see, however, § 4.2.1 on the role of ions). The mean magnetic field $\boldsymbol{B}_{\mathbf{0}}$ points in the positive $x$ direction, while the initial temperature gradient is set in the negative $x$ direction. The grid size measured in the electron Larmor radii $\unicode[STIX]{x1D70C}_{e1}$ at the left (hot) end of the box is fixed at $L_{x}\times L_{y}\approx 125\times 25\unicode[STIX]{x1D70C}_{e1}$ , and $\unicode[STIX]{x1D70C}_{e1}\approx 20$ cells. The electron temperature at the hot wall is such that the ratio of the thermal electron speed to the speed of light is $v_{\text{th}1}/c\approx 0.33$ . We vary the initial electron plasma $\unicode[STIX]{x1D6FD}_{e}=8\unicode[STIX]{x03C0}nT/B_{0}^{2}=(10,15,25,40)$ . For the run with $\unicode[STIX]{x1D6FD}_{e}=40$ , we increase the grid resolution by a factor of 1.5 to better resolve the electron skin depth $d_{e}$ . At the hot wall, where the particle density is the smallest (see below), $d_{e1}\approx (6.5,5.4,4.2,4.9)$ cells for the corresponding range of $\unicode[STIX]{x1D6FD}_{e}$ , which gives $\unicode[STIX]{x1D70C}_{e1}/d_{e1}\approx (3.1,3.7,4.8,6.1)$ .

For the electrons’ initial conditions in velocity space, we employ the isotropic Maxwell distribution with temperature $T_{0}(x)$ that decreases linearly from $T_{1}$ to $T_{2}$ along $x$ . $T_{1}$ is kept constant in all the runs, while $T_{2}$ is varied. We vary $T_{1}/T_{2}=(1.5,2,3)$ in runs with the same $\unicode[STIX]{x1D6FD}_{e}=15$ , while the scan over $\unicode[STIX]{x1D6FD}_{e}$ is performed at the same $T_{1}/T_{2}=2$ . The mean electron density $n_{0}$ is distributed so as to keep the electron pressure $p$ uniform across the box, i.e. $n_{0}(x)\propto 1/T_{0}(x)$ , and does not evolve in time (the electrons are bound to the ions by quasineutrality). This way, the initial distribution is close to what we expect to observe when the instability saturates by scattering and isotropizing the electrons, making the plasma effectively collisional. While the temperature gradient evolves in the simulation and is not strictly linear at saturation, setting the particle density $n_{0}(x)\propto 1/T_{0}(x)$ largely reduces spatial variations of pressure and, consequently, $\unicode[STIX]{x1D6FD}_{e}$ . Alternatively, we could have used a collisionless initial condition with uniform density and counterstreaming electrons at temperatures $T_{1}$ and $T_{2}$ , represented in velocity space by two (‘hotward’ and ‘coldward’) Maxwellian hemispheres with densities chosen so that the net electron current is zero. In this case, electron scattering would have led to formation of an additional mean electric field to compensate for the temperature (and, due to uniform density, pressure) gradient. We have tried both types of initial conditions and observed no significant differences in the properties of the saturated state, and thus use the former way in what follows.

Figure 2. The spatial structure of the $z$ -component of the magnetic field generated by the heat-flux-induced whistler instability. The magnetic-field lines are shown as the black contours. The temperature gradient points opposite to the $x$ axis, i.e. the heat flux is in the positive direction. The whistlers propagate in the direction of the heat flux from the hot (left) to the cold (right) wall. The walls are located ${\approx}10\unicode[STIX]{x1D70C}_{e1}$ away from the edges of the box. The regions behind the walls are used to dissipate the energy of the incident waves. The saturated state of the instability is characterized by oblique whistler propagation in a wide range of angles.

Proper boundary conditions are essential for simulations of an instability constantly driven by a sustained temperature gradient. For the particles, we use periodic boundary conditions along $y$ and reflective boundary conditions along $x$ . A particle reflected from a wall acquires a random velocity drawn from the velocity distribution function $f_{0}(\boldsymbol{v},T_{1,2})v_{x}$ , where $f_{0}$ is Maxwell’s distribution at temperature $T_{1,2}$ . This ensures that the incoming flux of particles colliding with a wall is equal to the flux of the reflected particles with new velocities. The reflected flux corresponds to a flow of Maxwellian particles at temperature $T_{1,2}$ from an infinite half-space through the plane of a wall.

For the electric and magnetic fields, we introduced absorbing boundary conditions to reduce reflection of the wave modes generated by the instability from the walls. We put thermal reservoirs of particles behind the walls. The reservoirs have width $L_{D}=192$ cells ( ${\sim}$ the typical wavelength of whistlers, i.e. several electron Larmor radii $\unicode[STIX]{x1D70C}_{e1}$ ). In the reservoirs, which serve as absorbers, the fields $\boldsymbol{B}$ and $\boldsymbol{E}$ are evolved to decay as (Umeda, Omura & Matsumoto 2001)

(3.1) $$\begin{eqnarray}\displaystyle \boldsymbol{B}^{n+1/2}(x) & = & \displaystyle \unicode[STIX]{x1D6FC}_{M}(x)\{\boldsymbol{B}^{n-1/2}(x)-c\unicode[STIX]{x0394}t\unicode[STIX]{x1D735}\times \boldsymbol{E}^{n}(x)\},\end{eqnarray}$$

(3.2) $$\begin{eqnarray}\displaystyle \boldsymbol{E}^{n+1/2}(x) & = & \displaystyle \unicode[STIX]{x1D6FC}_{M}(x)\{\boldsymbol{E}^{n-1/2}(x)-\unicode[STIX]{x0394}t[4\unicode[STIX]{x03C0}\boldsymbol{j}^{n}(x)-c\unicode[STIX]{x1D735}\times \boldsymbol{B}^{n}(x)]\},\end{eqnarray}$$

where $\boldsymbol{j}$ is the current density, $c$ the speed of light and $\unicode[STIX]{x0394}t$ the time step. The masking parameter $\unicode[STIX]{x1D6FC}_{M}(x)<1$ gradually decreases into the reservoirs in order to avoid numerical reflections at the absorber boundary:

(3.3) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{M}(x)=1-\left(r\frac{|x-x_{1,2}|}{L_{D}}\right)^{2}, & & \displaystyle\end{eqnarray}$$

where $x_{1,2}$ are the walls’ positions. The parameter $r\approx 0.02$ regulates the gradient of the masking function and is adjusted to utilize the width of the absorbing regions most effectively for a given group velocity of the waves (Umeda et al. 2001). One must put particles in the absorbers to reduce wave reflection by matching the impedance of the absorbers with the one of the plasma in the main domain near the walls. This provides good absorption for perpendicular wave incidence. For off-axis waves, however, some reflection is still present as can be seen at higher wave amplitudes in figure 2.

3.2 Results

3.2.1 Field structure

In the absence of scattering, the initial isotropic electron distribution with a temperature gradient in the negative $x$ direction is unstable to generation of whistlers propagating with a group velocity $v_{g}\sim v_{\text{th}}/\unicode[STIX]{x1D6FD}_{e}$ opposite to the temperature gradient, i.e. in the direction of the heat flux. The unstable right-hand polarized modes grow at the scale of ${\sim}10\unicode[STIX]{x1D70C}_{e}$ , practically independent of $\unicode[STIX]{x1D6FD}_{e}$ and $T_{1}/T_{2}$ ³ . The instability saturates in the state shown in figure 2. The presence of oblique modes in the final state is manifest.

The waves grow as they travel away from the hot wall and reach full saturation in the right half of the box. We plot the evolution of the mean magnetic-energy density in the perpendicular component of the magnetic field in figure 3. The time required by the instability to saturate completely is rather long, only a few times smaller than the time it takes the waves to cross the box, $t_{\text{cross}}\unicode[STIX]{x1D6FA}_{e}\sim L_{x}\unicode[STIX]{x1D6FD}_{e}/\unicode[STIX]{x1D70C}_{e}\sim 1000$ –4000. This leads to the magnetic perturbations at saturation noticeably growing along $x$ , reaching a plateau past the centre of the box. The final amplitude of these perturbations can be determined purely by quasilinear saturation only where the field becomes spatially homogeneous, whereas before that, wave advection likely plays a significant role, removing energy before quasilinear saturation fully comes into play. This is a consequence of non-periodic boundary conditions, and to alleviate the problem, one can either increase the box size, or simply calculate all the important quantities required to check theoretical assumptions in regions where the magnetic field is spatially homogeneous. Because the former route is quite computationally expensive, we have chosen the latter. We shall see that this does allow us to confirm our predictions.

Figure 3. Evolution of the mean perpendicular magnetic-energy density in whistler modes for runs with different $\unicode[STIX]{x1D6FD}_{e}$ and $T_{1}/T_{2}$ .

The 2-D power spectrum of the $z$ component (perpendicular to the picture plane in figure 2) of the magnetic field on scales larger than the electron Larmor radius is shown in figure 5 for runs with different $\unicode[STIX]{x1D6FD}_{e}$ . The power spectrum peaks at ${k_{\Vert }}^{\max }\unicode[STIX]{x1D70C}_{e}\approx 0.7$ , corresponding to the scale of ${\approx}10\unicode[STIX]{x1D70C}_{e}$ , mostly independently of $\unicode[STIX]{x1D6FD}_{e}$ . There is substantial power at all propagation angles, which confirms the hypothesis that the saturated marginal state is not restricted to parallel whistlers (as conjectured by Levinson & Eichler (1992) and shown using quasilinear theory by PE98). The width of the excited spectrum of whistlers can be seen to be $\unicode[STIX]{x0394}k_{\Vert }/{k_{\Vert }}^{\max }\sim 1$ .

Figure 4. Temperature profiles normalized by the temperature $T_{1}$ of the hot wall at saturation.

Figure 5. The logarithm of the 2-D power spectrum of the $z$ component of the magnetic field produced by the whistler instability for different values of $\unicode[STIX]{x1D6FD}_{e}$ and fixed $T_{1}/T_{2}=2$ . The contours correspond to logarithmic increments ${\approx}2.4$ . The spectrum has been calculated for the right third of the box, where the field power is even along $x$ in all the runs, and averaged over several time snapshots. The spectrum peaks at $k_{\Vert }\unicode[STIX]{x1D70C}_{e}\sim 0.7$ , largely independently of $\unicode[STIX]{x1D6FD}_{e}$ , as predicted by the linear theory. The magnetic energy is distributed over a broad range of angles rather than being concentrated along the parallel direction, thus potentially allowing effective scattering of particles propagating at any angles.

The profiles of electron temperature in the saturated state are shown in figure 4. They are seen to be close to linear, with the exception of the cases with the lowest and the highest $\unicode[STIX]{x1D6FD}_{e}$ , thus producing only minor variations of electron pressure over the box. The difference between the calculated temperature near the walls and the temperatures of the walls (and of the absorbing regions) is caused by the anisotropy of the electron distribution function: a larger anisotropy produces a bigger difference between the temperature of particles moving away from the wall with new thermal velocities and the temperature calculated by averaging over all directions of particle motion (as in the profiles). A larger $\unicode[STIX]{x1D6FD}_{e}$ leads to stronger magnetic perturbations, therefore a more isotropic electron distribution and smaller temperature difference between the plasma and the walls.

3.2.2 Marginal electron distribution

Let us analyse the perturbed part of the electron distribution function in our simulations. To do so, we calculate the distribution function in the right third of the box, average it over electron pitch angles, and subtract the averaged part from the calculated distribution. We do so for several time snapshots and average the distribution functions over them. In this manner, we obtain the perturbation associated with the heat flux and the instability. The shape of the perturbation is similar to the one we used as an illustrative example of the anisotropy produced by a heat flux in § 2.3, and is presented in figure 6 on the right, along with the total distribution function on the left. The distribution that we show here is a function of $v_{x}$ and $v_{z}$ , i.e. it has been integrated over $v_{y}$ . The central region of the perturbation ensures the current-free condition ⁴ . The outer parts, on the other hand, are those that drive the instability (recall figure 1). It is clear that larger $\unicode[STIX]{x1D6FD}_{e}$ reduce the overall anisotropy.

As we mentioned in § 2.4, for the dipole-shaped distribution resulting from the Knudsen expansion of the Boltzmann equation with an isotropic collision operator, parallel whistlers grow the fastest, while they do not interact with the coldward (right) heat-flux-carrying part of the distribution. A modification of the perturbation caused by scattering off the unstable modes, however, can result in a state favourable for generation of oblique modes, which brings both positive and negative gyroresonances into action. This may happen if initially the dipole perturbation generates parallel whistlers that resonate with the hotward-streaming electrons, which depletes the hotward part of the distribution. Then the final state becomes germane to oblique whistlers that grow and resonate with the coldward electrons. The asymmetry in the morphology of the perturbed distribution seen in figure 6 can be an indication of such a shift of marginal stability to oblique propagation ⁵ . It is especially vivid at larger $\unicode[STIX]{x1D6FD}_{e}$ : the hotward part of the distribution is significantly more depleted than the coldward part associated with the heat flux. This final state of the electron distribution function obtained in our simulations therefore can support the above picture.

Figure 6. The marginal electron distribution functions obtained from the simulations. The left column shows the total distribution function and demonstrates the isotropization of the distribution at higher $\unicode[STIX]{x1D6FD}_{e}$ . The right column shows the anisotropic part of the distribution function driven by the heat flux. Depletion of particles with negative (hotward) parallel velocities is clearly seen.

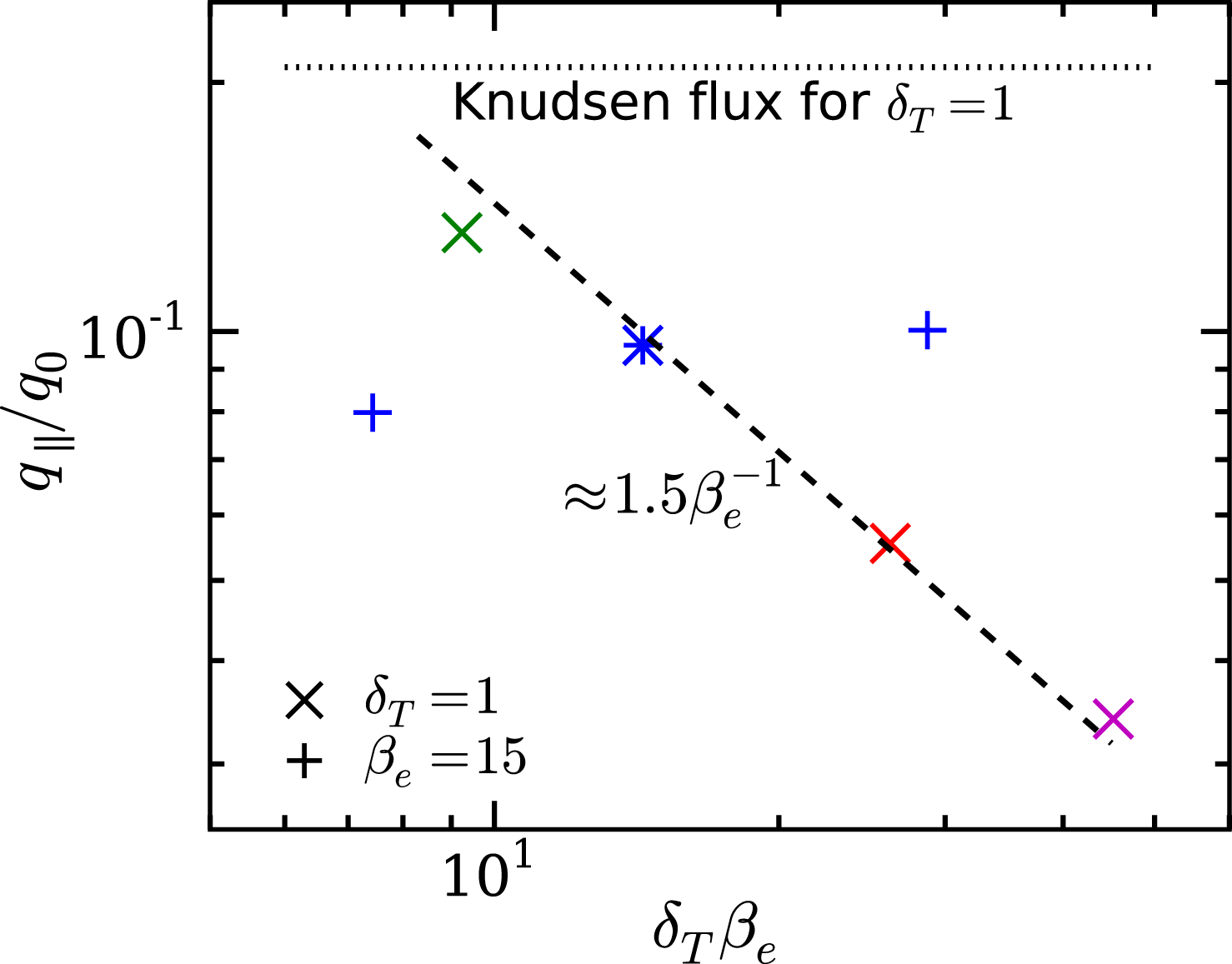
Figure 7. The heat fluxes measured in the numerical simulations as functions of $\unicode[STIX]{x1D6FF}_{T}\unicode[STIX]{x1D6FD}_{e}$ , where $\unicode[STIX]{x1D6FF}_{T}=T_{1}/T_{2}-1$ . The pluses represent the runs with the same plasma $\unicode[STIX]{x1D6FD}_{e}=15$ , while the crosses of the same colours as in figure 3 show the runs with the same temperature gradient $T_{1}/T_{2}=2$ . We have made corrections for the small variation of the mean thermal pressure (and, therefore, the effective $\unicode[STIX]{x1D6FD}_{e}$ ) in different runs.

3.2.3 Heat flux

Now we are in a position to examine whether the heat flux is indeed governed by the instability and limited by the marginal anisotropy. The fluxes are averaged over the computational domain (there is no systematic spatial variation of the heat flux at saturation, otherwise a build-up of energy would occur) and several time snapshots. As we anticipate suppression of the heat flux given by (2.22), it is convenient to normalize the flux by $q_{0}=\langle m_{e}nv_{\text{th}}^{3}\rangle \approx 2n_{1}T_{1}\langle v_{\text{th}}\rangle$ , where the angle brackets indicate averaging over the box, and we have taken the pressure $nT$ to be close to uniform across the box.

The heat flux as a function of $\unicode[STIX]{x1D6FF}_{T}\unicode[STIX]{x1D6FD}_{e}$ , $\unicode[STIX]{x1D6FF}_{T}=T_{1}/T_{2}-1$ , is shown in figure 7. At constant $\unicode[STIX]{x1D6FD}_{e}=15$ but different $T_{1}/T_{2}$ , there is only a small scatter in the heat flux as $\unicode[STIX]{x1D6FF}_{T}$ is varied by a factor of 4. This agrees with the qualitative expectation that the flux has no dependence on the imposed temperature gradient when the marginal state is reached (§ 2.1).

The heat fluxes taken at constant $\unicode[STIX]{x1D6FF}_{T}$ and different $\unicode[STIX]{x1D6FD}_{e}$ are well fitted by $q_{\Vert }/q_{0}\approx 1.5\unicode[STIX]{x1D6FD}_{e}^{-1}$ . We also show the collisionless Knudsen heat flux (also normalized by $q_{0}$ ) at the fixed $T_{1}/T_{2}=2$ to demonstrate the relative amount of suppression in the simulation. This heat flux corresponds to a velocity distribution composed of two Maxwellian hemispheres associated with two opposite electron fluxes from the respective walls with even electron density and no electric field. The Knudsen heat flux is the maximum flux attainable in any configuration with fixed $T_{1}$ and $T_{2}$ , and is equal to

(3.4) $$\begin{eqnarray}\displaystyle q_{K}=\frac{1}{\sqrt{\unicode[STIX]{x03C0}}}m_{e}n_{0}[\unicode[STIX]{x1D6FC}v_{\text{th}1}^{3}-(1-\unicode[STIX]{x1D6FC})v_{\text{th}2}^{3}], & & \displaystyle\end{eqnarray}$$

where $n_{0}$ is the mean electron density (density is even in a completely collisionless plasma), $\unicode[STIX]{x1D6FC}$ and $1-\unicode[STIX]{x1D6FC}$ represent the fractions of particles moving in the coldward and hotward directions respectively in order to make for zero net electron current, viz.,

(3.5) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}(T_{1},T_{2})=\left[1+\left(\frac{T_{1}}{T_{2}}\right)^{1/2}\exp \frac{T_{1}-T_{2}}{T_{1}T_{2}}\right]^{-1}. & & \displaystyle\end{eqnarray}$$

We see that if our fit of the $\unicode[STIX]{x1D6FD}$ dependence is correct, no suppression below $\unicode[STIX]{x1D6FD}_{e}\sim 10$ should be present. This could be the reason why the data point at $\unicode[STIX]{x1D6FD}_{e}\approx 10$ is a slight outlier.

Clearly, the simple argument in § 2 based on saturation in the marginal state of the whistler instability indeed leads to conclusions supported by numerical simulations. Thus, we expect the heat flux to be fully controlled by the instability and not being able to exceed its marginal value (2.22): for the general case of a plasma with a small temperature gradient,

(3.6) $$\begin{eqnarray}\displaystyle q_{\Vert }^{\max }\approx 1.5\unicode[STIX]{x1D6FD}_{e}^{-1}nv_{\text{th}}^{3}. & & \displaystyle\end{eqnarray}$$

3.2.4 Scattering rate and saturated magnetic field

In § 2.5, based on Bohm diffusion and the whistler marginality condition (2.21), we estimated the effective pitch-angle scattering rate as a function of $\unicode[STIX]{x1D6FD}_{e}$ and the ratio of the electron Larmor radius $\unicode[STIX]{x1D70C}_{e}$ and temperature scale length $L_{T}$ . In order to test this prediction, we obtain the scattering rate $\unicode[STIX]{x1D708}_{\text{scatt}}$ from the simulations by tracing a large number ( ${\sim}10\,000$ ) of test electrons, calculating their mean spatial spread along the mean magnetic field, and estimating the parallel diffusion coefficient $D_{\Vert }=(1/3)v_{\text{th}}^{2}/\unicode[STIX]{x1D708}_{\text{scatt}}$ for runs with different $\unicode[STIX]{x1D6FD}_{e}$ as follows:

(3.7) $$\begin{eqnarray}\displaystyle D_{\Vert }=\frac{1}{2}\frac{\text{d}\langle [x_{i}(t_{\text{diff}})-x_{i}(0)]^{2}\rangle }{\text{d}t}, & & \displaystyle\end{eqnarray}$$

where $x_{i}$ is the $x$ coordinate of particle $i$ and time $t_{\text{diff}}$ is taken sufficiently long for diffusion to settle. We then average $L_{T}=T/\unicode[STIX]{x2202}_{x}T$ and $\unicode[STIX]{x1D70C}_{e}$ over the computation domain for each run and plot $\unicode[STIX]{x1D708}_{\text{scatt}}L_{T}/\unicode[STIX]{x1D70C}_{e}$ as a function of $\unicode[STIX]{x1D6FD}_{e}$ . The result is shown in figure 8. There is a good agreement with the qualitative prediction that testifies in favour of quasilinear saturation. Calculating the diffusion coefficient the way we do for the run with the highest $\unicode[STIX]{x1D6FD}_{e}=40$ is likely not fully consistent due to the large variations of magnetic perturbations across the box and their large amplitude.

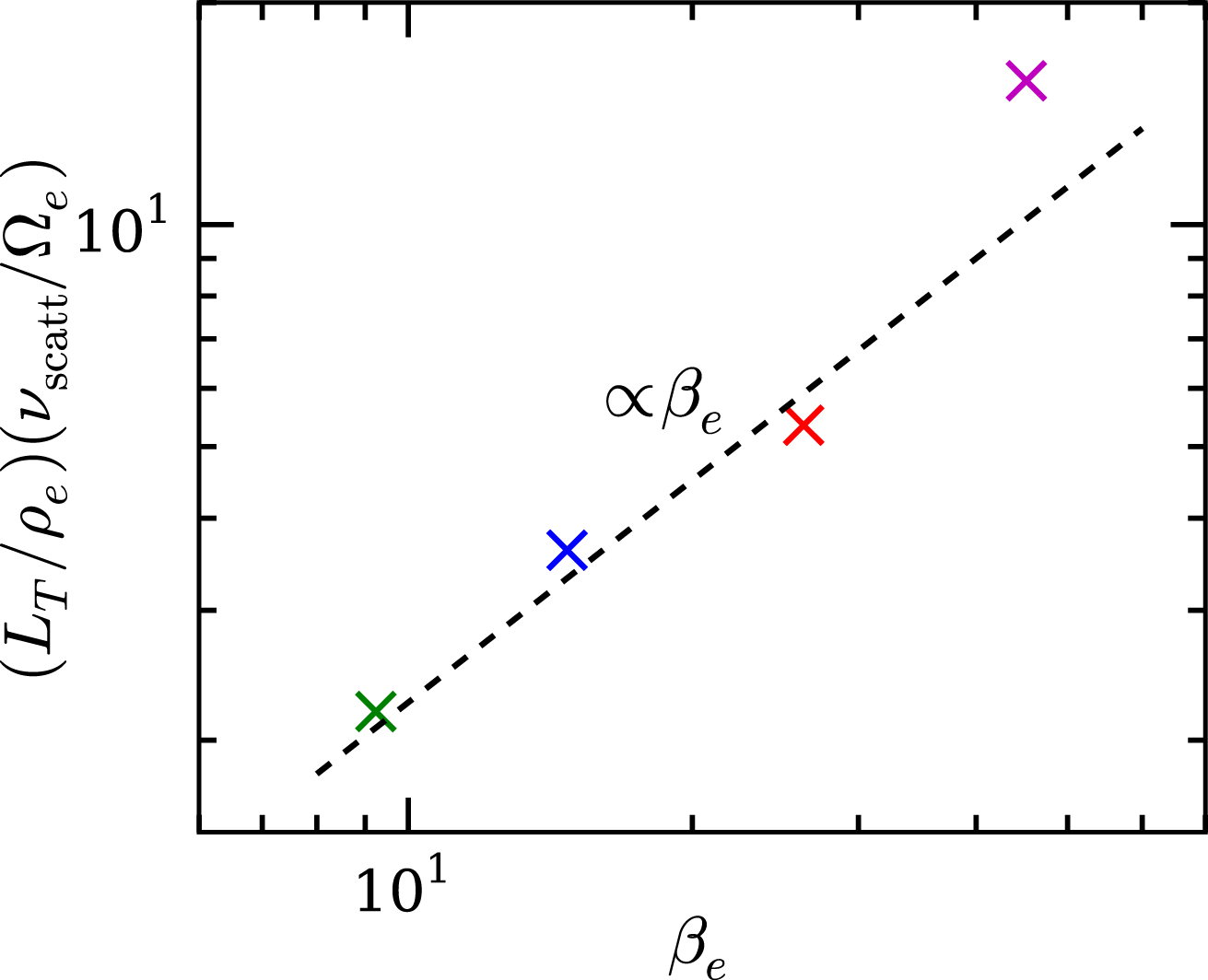
Figure 8. The electron scattering rate multiplied by $L_{T}/\unicode[STIX]{x1D70C}_{e}$ (which varies in different runs because of the different final temperature profiles and equals ${\sim}100$ on average) as a function of $\unicode[STIX]{x1D6FD}_{e}$ . The temperature scale length $L_{T}=T/\unicode[STIX]{x2202}_{x}T$ and the electron Larmor radius $\unicode[STIX]{x1D70C}_{e}$ have been averaged over the simulation domain. We have corrected for the small variation of the effective $\unicode[STIX]{x1D6FD}_{e}$ in different runs, as in figure 7. The dashed line shows the prediction (2.26) based on Bohm diffusion combined with the whistler marginality condition.

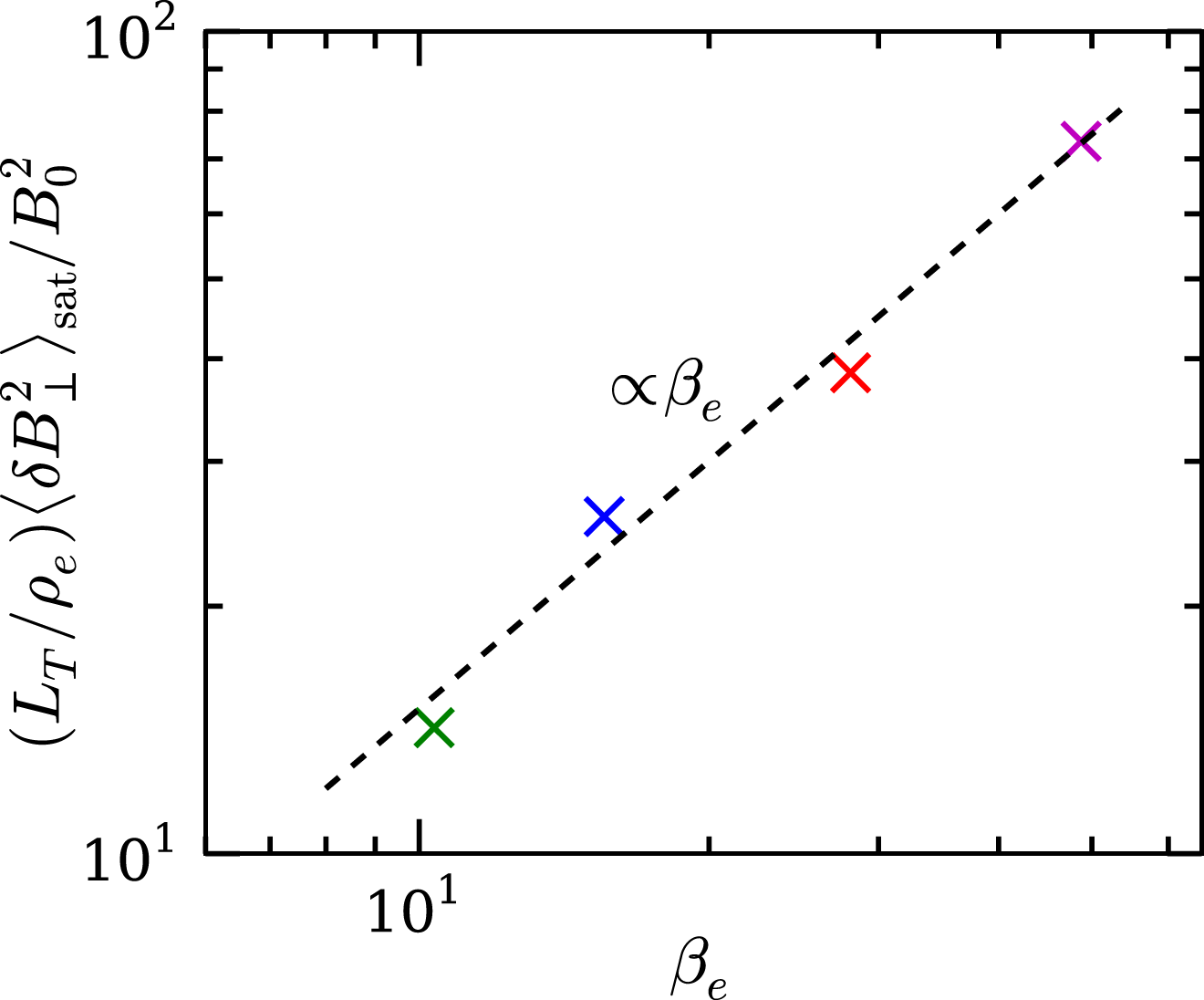
Figure 9. The saturated perpendicular magnetic-field energy density multiplied by $L_{T}/\unicode[STIX]{x1D70C}_{e}$ (different in different runs, ${\sim}100$ ) as a function of $\unicode[STIX]{x1D6FD}_{e}$ . The field is averaged over the right third of the computation domain, where it is fully saturated and homogeneous, and also over several time snapshots. The temperature scale length $L_{T}=T/\unicode[STIX]{x2202}_{x}T$ and the electron Larmor radius $\unicode[STIX]{x1D70C}_{e}$ are averaged similarly. We have corrected for the effective $\unicode[STIX]{x1D6FD}_{e}$ in the averaging region. The dashed line is a comparison with the prediction (2.28) based on Bohm diffusion combined with the whistler marginality condition.

We can also check if the simple estimate of the saturated magnetic field (2.28) based on Bohm diffusion applies to the simulated field. We average the perpendicular magnetic-energy density over the right third of the box, where it is fully saturated and homogeneous in all the runs, and over several time snapshots. $L_{T}$ and $\unicode[STIX]{x1D70C}_{e}$ are again averaged analogously. Similar to the scattering rate, we plot the magnetic-energy density multiplied by $L_{T}/\unicode[STIX]{x1D70C}_{e}$ in figure 9. The Bohm formula describes the simulation results well for practically all $\unicode[STIX]{x1D6FD}_{e}$ .

4 Discussion

4.1 Relevance to clusters of galaxies

The intracluster medium (ICM) is a hot rarefied plasma with the typical range of $\unicode[STIX]{x1D6FD}_{e}$ (recall that the total $\unicode[STIX]{x1D6FD}_{\text{tot}}=\unicode[STIX]{x1D6FD}_{e}+\unicode[STIX]{x1D6FD}_{i}$ often used in literature is approximately twice larger) between several tens and several hundred (see, e.g. Kuchar & Ensslin 2011). Thermal conduction may or may not play a role in several contexts. One is affecting global radial temperature profiles, the knowledge of which is necessary to calculate cluster masses from X-ray observations. In this case, temperature gradients are small, i.e. temperature scale lengths are long, of the order of several hundreds of kpc. Another is the possibility of existence of smaller-scale temperature substructure, including cold fronts, where temperature gradients can be rather large (e.g. Ichinohe et al. 2015; Wang et al. 2016), with the temperature scale length approaching the classical Spitzer mean free path ( ${\sim}1$ –10 kpc).

The suppression of heat flux caused by whistlers is important only if the upper limit on the flux imposed by the instability, $q_{\Vert w}$ , turns out to be smaller than the Spitzer heat flux (Spitzer & Härm 1953). The modified Spitzer heat flux $q_{\Vert S}$ , which includes saturation of the flux when large gradients are present on scales smaller than the electron Coulomb mean free path, can be expressed conveniently as (Cowie & McKee 1977; Sarazin 1988)

(4.1) $$\begin{eqnarray}\displaystyle q_{\Vert S}\approx 0.5m_{e}nv_{\text{th}}^{3}\frac{\unicode[STIX]{x1D706}_{e}}{L_{T}+4\unicode[STIX]{x1D706}_{e}}, & & \displaystyle\end{eqnarray}$$

where $L_{T}$ is the parallel temperature gradient scale, and $\unicode[STIX]{x1D706}_{e}$ is the mean free path for the electron energy exchange. Equation (4.1) interpolates between the classical collisional regime $\unicode[STIX]{x1D706}_{e}\ll L_{T}$ and the collisionless saturated flux at an infinite temperature gradient. The latter is obtained by assuming a hot plasma adjoining a cold absorber, with a self-consistent electric field set up to stop the current. The free molecular conductivity in this case is taken to be reduced by the electric field by the same factor of 0.4 as in the classical case (Spitzer & Härm 1953). Other estimates give values of saturated flux by a factor of a few larger (see Cowie & McKee 1977). Thus, our estimate of suppression compared to the unmagnetized saturated heat flux may be considered conservative. The ratio of the two fluxes is the suppression factor $S_{w}<1$ ,

(4.2) $$\begin{eqnarray}\displaystyle S_{w}=\frac{q_{\Vert w}}{q_{\Vert S}}\approx \frac{3}{\unicode[STIX]{x1D6FD}_{e}}\left(\frac{L_{T}}{\unicode[STIX]{x1D706}_{e}}+4\right). & & \displaystyle\end{eqnarray}$$

It is easy to write an expression for the effective parallel heat flux $q_{\Vert \text{eff}}$ that interpolates between the Spitzer flux, when the suppression factors are close to unity, and the flux controlled by whistlers, when suppression is large:

(4.3) $$\begin{eqnarray}\displaystyle q_{\Vert \text{eff}}=\frac{q_{\Vert S}}{1+\unicode[STIX]{x1D6FD}_{e}/3(L_{T}/\unicode[STIX]{x1D706}_{e}+4)^{-1}}\approx \frac{0.5m_{e}nv_{\text{th}}^{3}}{L_{T}/\unicode[STIX]{x1D706}_{e}+\unicode[STIX]{x1D6FD}_{e}/3+4}. & & \displaystyle\end{eqnarray}$$

Equation (4.3) can be used for heat-flux estimates in problems where plasma kinetic effects are otherwise ignored, or as a simple subgrid model in numerical simulations.

For the typical parameters of the hot ICM, the energy-exchange electron mean free path is (e.g. Sarazin 1988)

(4.4) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}_{e}\approx 20~\text{kpc}\left(\frac{T}{10^{8}~\text{K}}\right)^{2}\left(\frac{n}{10^{-3}~\text{cm}^{-3}}\right)^{-1}. & & \displaystyle\end{eqnarray}$$

Let us assume $\unicode[STIX]{x1D6FD}_{e}\sim 100$ to estimate the maximum suppression of thermal conduction possible. The maximum suppression is reached at $L_{T}\ll \unicode[STIX]{x1D706}_{e}$ where $S_{w}\sim 1/10$ . Such small scale lengths of the temperature gradient along the mean magnetic field, however, are unrealistic in galaxy clusters. Even in cold fronts, where $L_{T}\lesssim \unicode[STIX]{x1D706}_{e}$ , the magnetic field is very likely draped perpendicular to the gradient, and thus the parallel gradient scale should be appreciably larger. At larger scales, suppression drops linearly: $S_{w}\sim 1/4$ at 100 kpc, $S_{w}\sim 1/2$ at 300 kpc, and no suppression at ${\sim}600~\text{kpc}$ . We conclude, therefore, that in general, the suppression factors caused by the whistler instability are rather modest, and are unlikely to affect global radial temperature profiles strongly, or, e.g. cutoff cool cores from the heat supply from the outer hot regions in the absence of other suppression mechanisms. The effect can become more important if there are strong thermal gradients on intermediate and small scales ${\lesssim}100~\text{kpc}$ , where it becomes of the same order as the suppression by the mirror instability (Komarov et al. 2016) in case these scales are turbulent. The combination of the two effects is capable of producing suppression of order $1/30$ , which is sufficient to explain the variety of substructures typically observed in the ICM.

Finally, we comment on the possible relevance of the heat-flux suppression by whistlers to the thermal instability in galaxy clusters. Cold ( $T\sim 10^{4}~\text{K}$ ) H $\unicode[STIX]{x1D6FC}$ filaments are ubiquitously found in cluster cores (e.g. McDonald et al. 2010). Such structures are thought to be produced either by dragging the cold material out from central galaxies by buoyant radio bubbles (e.g. Churazov et al. 2001; Fabian et al. 2003), or by runaway cooling in the ICM (e.g. McCourt et al. 2012). In the latter case, during the early phase of a local thermal instability, when the plasma is not yet significantly compressed, so $\unicode[STIX]{x1D6FD}$ is still large, the extra suppression provided by whistlers could promote the development of the instability along the magnetic-field lines (see Boehringer & Fabian (1989) for a model of spherical cold clump formation in a non-magnetized plasma and Sharma, Parrish & Quataert (2010) for the magnetized case). The spatial scale at which cooling is balanced by thermal conduction is known as the field length $\unicode[STIX]{x1D706}_{F}$ (Field 1965). Assuming an initial spectrum of density perturbations dominated by small scales ( ${\lesssim}1~\text{kpc}$ ), thermal conduction begins to smear the perturbations along the magnetic-field lines on scales below $\unicode[STIX]{x1D706}_{F}$ , producing filamentary structures (alternatively, the elongated shape can be produced by motions in a stratified atmosphere with no magnetic field and no conduction; see, e.g. McCourt et al. 2012). While later in the evolution the density perturbations can continue to fragment into much shorter segments due to the decrease of $\unicode[STIX]{x1D706}_{F}$ , the large-scale coherence (see Fabian et al. (2008) for a high-resolution observational example) set by the parallel heat fluxes during the early phase should be preserved. In the perpendicular direction, there is no conduction, and the gas is compressed until it is stabilized by, e.g. the pressure support of cosmic rays or magnetic fields. Therefore, if the length of filaments in the thermal instability scenario is set mainly by parallel conduction, its suppression may lead to shorter filaments.

4.2 Limitations of the model

4.2.1 Importance of ions

In our simulations and theoretical model, ions do not participate in the instability and form a charge-neutralizing background. However, the phase speed of the unstable whistlers, $v_{\text{ph}}\sim v_{\text{th}e}/\unicode[STIX]{x1D6FD}_{e}$ , approaches the ion thermal speed, $v_{\text{th}i}=(m_{e}/m_{i})^{1/2}v_{\text{th}e}$ , at $\unicode[STIX]{x1D6FD}_{e}\sim 40$ . Therefore, oblique whistlers with non-zero parallel electric field may be damped by the ions via Landau resonance.

Figure 10. The spatial structure of the $z$ -component of the magnetic field generated by the heat-flux-induced whistler instability in the run with ions. The mass ratio is $m_{i}/m_{e}=225$ , the electron plasma $\unicode[STIX]{x1D6FD}_{e}=15$ , so the ions are roughly in Landau resonance with the whistlers. This run can be compared with the corresponding electron-only run (second panel from the top in figure 2).

In order to test how important the ion physics might be, we have performed a run with mass ratio $m_{i}/m_{e}=225$ , $\unicode[STIX]{x1D6FD}_{e}=15$ , and $T_{1}/T_{2}=2$ , i.e. with the ions roughly in resonance with the unstable modes. All the other parameters of the simulations have been kept unchanged compared with the corresponding main electron-only run. Note that the ion Larmor radius in the new run is rather large, $\unicode[STIX]{x1D70C}_{i}\approx 300$ cells. For studying the effect of Landau resonance, however, the ion Larmor scale should not be important as long as $k_{\bot }\unicode[STIX]{x1D70C}_{i}\gg 1$ .

The ions do produce a noticeable change in the evolution of the instability. Namely, they somewhat delay full saturation. However, the final spatial structure of the magnetic field looks similar to the corresponding electron-only run, with the saturated field amplitude only ${\sim}15\,\%$ smaller (see figure 10). The heat flux at saturation is roughly 20 % larger. We have not explored the full range of $\unicode[STIX]{x1D6FD}_{e}$ and $T_{1}/T_{2}$ including the ions, but our test run gives us some confidence that even close to the Landau resonance, the ions do not seem to choke the instability, and our main results remain correct within factors of order unity.

In addition to the above, at sufficiently high $\unicode[STIX]{x1D6FD}_{e}\sim m_{i}/m_{e}$ , the cyclotron resonance with the ions, $\unicode[STIX]{x1D714}\sim \unicode[STIX]{x1D6FA}_{e}/\unicode[STIX]{x1D6FD}_{e}\sim \unicode[STIX]{x1D6FA}_{i}$ comes into play, and our theoretical assumptions may break down. But even in this case, simple qualitative arguments based on the analysis of the whistler dispersion relation for the case of small propagation angles can be made to show that such damping should not exceed the electron cyclotron damping, and, therefore, the suppression of heat flux should not be affected radically. First, it is safe to assume that the real part of the whistler dispersion relation $D(\unicode[STIX]{x1D714},\boldsymbol{k})=0$ is largely dominated by the electron contribution (see, e.g. Treumann & Baumjohann 1997). Then, we can compare the imaginary parts $D_{\text{im},e}$ and $D_{\text{im},i}$ (that lead to damping) due to the electrons and ions respectively (Treumann & Baumjohann 1997):

(4.5) $$\begin{eqnarray}\displaystyle D_{\text{im},e} & = & \displaystyle \frac{\unicode[STIX]{x03C0}^{1/2}\unicode[STIX]{x1D714}_{pe}^{2}}{k_{\Vert }v_{\text{th}e\Vert }\unicode[STIX]{x1D714}}\exp \left[-\left(\frac{\unicode[STIX]{x1D6FA}_{e}-\unicode[STIX]{x1D714}}{k_{\Vert }v_{\text{th}e\Vert }}\right)^{2}\right],\end{eqnarray}$$

(4.6) $$\begin{eqnarray}\displaystyle D_{\text{im},i} & = & \displaystyle \frac{\unicode[STIX]{x03C0}^{1/2}\unicode[STIX]{x1D714}_{pi}^{2}}{k_{\Vert }v_{\text{th}i\Vert }\unicode[STIX]{x1D714}}\exp \left[-\left(\frac{\unicode[STIX]{x1D6FA}_{i}+\unicode[STIX]{x1D714}}{k_{\Vert }v_{\text{th}i\Vert }}\right)^{2}\right].\end{eqnarray}$$

Using $(\unicode[STIX]{x1D6FA}_{i}+\unicode[STIX]{x1D714})/k_{\Vert }v_{\text{th}i\Vert }\sim \unicode[STIX]{x1D6FA}_{i}/k_{\Vert }v_{\text{th}i\Vert }\sim (m_{e}/m_{i})^{1/2}\ll 1$ and $(\unicode[STIX]{x1D6FA}_{e}-\unicode[STIX]{x1D714})/k_{\Vert }v_{\text{th}e\Vert }\sim \unicode[STIX]{x1D6FA}_{e}/k_{\Vert }v_{\text{th}e\Vert }\sim 1$ , we can obtain the ratio

(4.7) $$\begin{eqnarray}\displaystyle D_{\text{im},e}/D_{\text{im},i}\sim (m_{i}/m_{e})^{1/2}\text{e}^{-1}\sim 10. & & \displaystyle\end{eqnarray}$$

We see now that the ion cyclotron damping term is significantly smaller than the electron one. This can be understood if one notes that in cyclotron resonance $\unicode[STIX]{x1D714}\sim \unicode[STIX]{x1D6FA}_{i}$ , an ion travels parallel distance ${\sim}\unicode[STIX]{x1D70C}_{i}\gg \unicode[STIX]{x1D70C}_{e}\sim k_{\Vert }^{-1}$ over one gyration period, thus intersecting many parallel whistler wavelengths and significantly reducing the efficiency of the wave–ion interaction compared to the electron cyclotron resonance. This quick calculation indicates that even at $\unicode[STIX]{x1D6FD}_{e}\sim 2000$ our model may still be usable ⁶ .

We should stress that the above discussion does not deny the need for proper numerical modelling of the heat-flux-induced whistler instability with ion physics, but is aimed to support at least the qualitative usefulness of our model in light of the seemingly problematic issue of ion resonances appearing already at modest $\unicode[STIX]{x1D6FD}_{e}\lesssim 100$ .

4.2.2 Reaching regime of small magnetic perturbations

In astrophysical environments, temperature-gradient scales exceed electron Larmor radii by many orders of magnitude. Therefore, the heat-flux-induced whistler instability in these environments saturates at a very low level, as described by (2.28). Numerically, such a regime is demanding to simulate. First, if one needs to study suppression of thermal conduction by the instability, $\unicode[STIX]{x1D6FD}_{e}$ should be sufficiently large, at least $\unicode[STIX]{x1D6FD}_{e}>10$ , as we have shown first in § 3.2.3, and then, in relation to galaxy clusters, in § 4.1. Then either the temperature difference between the hot and cold walls should be set small, or the computation domain should be made long to minimize $\unicode[STIX]{x1D70C}_{e}/L_{T}$ . The former is problematic because the initial collisionless Knudsen heat flux in the absence of electromagnetic fields can be already too small, below the marginal level of the instability. Thus, we are left with the need to use a rather long simulation box. This is also dictated by the requirement that wave advection should not affect the saturation level in most of the box, as we have discussed in § 3.2.1. Our simulations show, however, that even the rather long box that we use provides only a narrow range of $\unicode[STIX]{x1D6FD}_{e}$ in which magnetic perturbations could be assumed small. Already at $\unicode[STIX]{x1D6FD}_{e}=25$ perturbations reach amplitudes $\unicode[STIX]{x1D6FF}B/B_{0}\sim 1$ . In this regard, we need to be confident that the suppression mechanism in the simulation has been identified correctly.

4.2.3 Possibility of alternative saturation mechanisms

Different nonlinear saturation mechanisms can by ruled out to a certain extent by comparison of nonlinear wave damping rates with the quasilinear damping rate (2.24). Additionally, one can compare the behaviour of the predicted nonlinear saturation levels as functions of $\unicode[STIX]{x1D6FD}_{e}$ by equating the linear growth rate and nonlinear damping rate. Such predictions are usually only possible under a number of drastically simplifying assumptions.

Let us consider nonlinear mode coupling first. Levinson & Eichler (1992) proposed it as a saturation mechanism of the instability. Levinson (1992) calculated the rate of nonlinear whistler mode coupling by using a perturbation approach in the approximation of near-parallel, $k_{\bot }/k_{\Vert }\ll 1$ , propagation (which is a questionable assumption at best in our case, but also the one that permits us to obtain a qualitative estimate):

(4.8) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{\text{MC}}\sim \frac{\unicode[STIX]{x1D708}_{\text{scatt}}}{\unicode[STIX]{x1D6FD}_{e}}\sim \frac{v_{\text{th}}}{\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{e}L_{T}}, & & \displaystyle\end{eqnarray}$$

where we have used $\unicode[STIX]{x1D708}_{\text{scatt}}=v_{\text{th}}/\unicode[STIX]{x1D706}_{\text{mfp}}=v_{\text{th}}/\unicode[STIX]{x1D716}L_{T}$ and $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D706}_{\text{mfp}}/L_{T}$ . By requiring the linear growth rate $\unicode[STIX]{x1D6FE}_{\text{lin}}\sim \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FA}_{e}$ to be balanced by nonlinear damping, we get

(4.9) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}=(\unicode[STIX]{x1D70C}_{e}/\unicode[STIX]{x1D6FD}_{e}L_{T})^{1/2}, & & \displaystyle\end{eqnarray}$$

and

(4.10) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{\text{MC}}\sim \frac{v_{\text{th}}}{(\unicode[STIX]{x1D6FD}_{e}\unicode[STIX]{x1D70C}_{e}L_{T})^{1/2}}. & & \displaystyle\end{eqnarray}$$

The quasilinear damping rate is $\unicode[STIX]{x1D6FE}_{\text{QL}}\sim \unicode[STIX]{x1D6FD}_{e}^{-1}\unicode[STIX]{x1D6FA}_{e}$ , and is seen to be a factor of

(4.11) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FE}_{\text{QL}}}{\unicode[STIX]{x1D6FE}_{\text{MC}}}\sim \left(\frac{L_{T}}{\unicode[STIX]{x1D6FD}_{e}\unicode[STIX]{x1D70C}_{e}}\right)^{1/2} & & \displaystyle\end{eqnarray}$$

larger than the rate of mode coupling. This factor is very large in astrophysical plasmas. In the simulation, however, it approaches unity at higher $\unicode[STIX]{x1D6FD}_{e}$ . In order to make a more detailed comparison, we can estimate the saturation level of magnetic perturbations from Bohm diffusion, $\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}\sim \unicode[STIX]{x1D708}_{\text{scatt}}/\unicode[STIX]{x1D6FA}_{e}$ , and substitute $\unicode[STIX]{x1D708}_{\text{scatt}}$ using equations (4.8) and (4.9):

(4.12) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}B^{2}}{B_{0}^{2}}\sim \left(\frac{\unicode[STIX]{x1D6FD}_{e}\unicode[STIX]{x1D70C}_{e}}{L_{T}}\right)^{1/2}. & & \displaystyle\end{eqnarray}$$

We see that the saturation level scales differently with $\unicode[STIX]{x1D6FD}_{e}$ and $\unicode[STIX]{x1D70C}_{e}/L_{T}$ than in our simulation. This gives us some confidence that the saturation is not regulated by mode coupling in our results. The nonlinear Landau damping rate can also be estimated in the same approximation, but is found to be an order of $\unicode[STIX]{x1D6FD}_{e}^{2}$ smaller than the mode coupling term (Levinson 1992).

Alternatively, when magnetic perturbations grow large and electron orbits become distorted, the instability may saturate by resonance broadening. Resonance broadening leads to leakage of particles out of the resonance until saturation is reached. This is modelled by the delta function in (2.12) substituted by the Lorenz function with a width set by electron scattering off magnetic perturbations. Using frequencies in place of momenta,

(4.13) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D714}-k_{\Vert }v_{\Vert }\pm \unicode[STIX]{x1D6FA}_{e})\longrightarrow \frac{\unicode[STIX]{x1D6FF}_{r}}{(\unicode[STIX]{x1D714}-k_{\Vert }v_{\Vert }\pm \unicode[STIX]{x1D6FA}_{e})^{2}+\unicode[STIX]{x1D6FF}_{r}^{2}}, & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D6FF}_{r}=(k_{\Vert }^{2}D/3)^{1/3}$ is the frequency half-width of the particle resonance and $D$ is the electron velocity diffusion coefficient (see, e.g. Treumann & Baumjohann 1997). The instability is stabilized when the resonance broadens beyond the width of the region of resonant particles in velocity space $\unicode[STIX]{x0394}v_{\Vert }$ , which can be roughly estimated as $\unicode[STIX]{x0394}v_{\Vert }\sim v_{\text{th}}$ (recall that the spectrum of excited waves is wide, $\unicode[STIX]{x0394}k_{\Vert }/k_{\Vert }\sim 1$ , and so is the resonant region in velocity space). Taking $D\sim v_{\text{th}}^{2}\unicode[STIX]{x1D708}_{\text{scatt}}\sim v_{\text{th}}^{2}\unicode[STIX]{x1D6FA}_{e}\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}$ from Bohm diffusion (assume that only the direction of electron velocity changes during scattering) as before, we are able to obtain the saturation level from the condition $\unicode[STIX]{x1D6FF}_{r}\sim k_{\Vert }v_{\text{th}}$ :

(4.14) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}B^{2}}{B_{0}^{2}}\sim \frac{k_{\Vert }v_{\text{th}}}{\unicode[STIX]{x1D6FA}_{e}}\sim 1, & & \displaystyle\end{eqnarray}$$

where we have used the fact that the resonant scale is virtually independent of the temperature gradient and $\unicode[STIX]{x1D6FD}_{e}$ . Thus, resonant broadening should lead to a saturated magnetic field whose amplitude does not depend on $\unicode[STIX]{x1D6FD}_{e}$ , in contradiction with our numerical results.

The above qualitative arguments appear to strengthen our point that the main saturation mechanism of the heat-flux-induced whistler instability both in astrophysical environments and our simulations has been identified correctly.

5 Conclusions

Aided by numerical simulations, we have demonstrated that, in the presence of a temperature gradient, a weakly collisional high- $\unicode[STIX]{x1D6FD}$ plasma is susceptible to the whistler instability. The instability quickly develops a spectrum of oblique modes that are able to scatter the heat-flux-carrying electrons. We have also confirmed the quasilinear result that at saturation, the marginal level of the heat flux is set by the inverse plasma $\unicode[STIX]{x1D6FD}$ rather than by the imposed temperature gradient. The numerical results have been shown to be in agreement with simple quasilinear arguments, such as the linear scaling of the pitch-angle scattering rate and the saturation level of magnetic perturbations with $\unicode[STIX]{x1D6FD}_{e}$ . In the context of galaxy clusters, the instability can introduce moderate suppression factors of thermal conduction ${\sim}1/4$ on scales ${\sim}100~\text{kpc}$ if significant variations of temperature are found there. We have given a simple expression (4.3) for the amount of suppression of the heat flux as a function of the temperature gradient scale length and the plasma $\unicode[STIX]{x1D6FD}$ . This expression can be applied to models in which kinetic effects are difficult to implement directly. Combined with the suppression by the mirror instability in a turbulent high- $\unicode[STIX]{x1D6FD}$ plasma, the two effects add up causing large suppression factors (several tens in the case of galaxy clusters).