Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-13T06:41:04.702Z Has data issue: false hasContentIssue false
  • English
  • Français

Simulation study of the formation of a non-relativistic pair shock

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  23 January 2017

M. E. Dieckmann Open the ORCID record for M. E. Dieckmann [Opens in a new window]  and
A. Bret
M. E. Dieckmann*
Affiliation:
Department of Science and Technology (ITN), Linkoping University, Campus Norrkoping, 60174 Norrkoping, Sweden
A. Bret
Affiliation:
University of Castilla La Mancha, ETSI Ind, E-13071 Ciudad Real, Spain Instituto de Investigaciones Energéticas y Aplicaciones Industriales, Campus Universitario de Ciudad Real, 13071 Ciudad Real, Spain
*
†Email address for correspondence: mark.e.dieckmann@liu.se
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine with a particle-in-cell (PIC) simulation the collision of two equally dense clouds of cold pair plasma. The clouds interpenetrate until instabilities set in, which heat up the plasma and trigger the formation of a pair of shocks. The fastest-growing waves at the collision speed 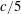$c/5$, where $c$ is the speed of light in vacuum, and low temperature are the electrostatic two-stream mode and the quasi-electrostatic oblique mode. Both waves grow and saturate via the formation of phase space vortices. The strong electric fields of these nonlinear plasma structures provide an efficient means of heating up and compressing the inflowing upstream leptons. The interaction of the hot leptons, which leak back into the upstream region, with the inflowing cool upstream leptons continuously drives electrostatic waves that mediate the shock. These waves heat up the inflowing upstream leptons primarily along the shock normal, which results in an anisotropic velocity distribution in the post-shock region. This distribution gives rise to the Weibel instability. Our simulation shows that even if the shock is mediated by quasi-electrostatic waves, strong magnetowaves will still develop in its downstream region.

Keywords

plasma instabilitiesplasma nonlinear phenomenaplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 1 , February 2017 , 905830104
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arber, T. D., Bennett, K., Brady, C. S., Lawrence-Douglas, A., Ramsay, M. G., Sircombe, N. J., Gillies, P., Evans, R. G., Schmitz, H., Bell, A. R. et al. 2015 Contemporary particle-in-cell approach to laser–plasma modelling. Plasma Phys. Control. Fusion 57, 113001.CrossRefGoogle Scholar
Baalrud, S. D., Callen, J. D. & Hegna, C. C. 2009 Instability-enhanced collisional effects and langmuir’s paradox. Phys. Rev. Lett. 102, 245005.CrossRefGoogle ScholarPubMed
Bale, S. D., Hull, A., Larson, D. E., Lin, R. P., Muschietti, L., Kellog, P. J., Goetz, K. & Monson, S. J. 2002 Electrostatic turbulence and debye-scale structures associated with electron thermalization at collisionless shocks. Astrophys. J. 575, L25–L28.CrossRefGoogle Scholar
Berk, H. L. & Roberts, K. V. 1967 Nonlinear study of vlasov’s equation for a special class of distribution functions. Phys. Fluids 10, 1595–1597.CrossRefGoogle Scholar
Brainerd, J. J. 2000 A plasma instability theory of gamma-ray burst emission. Astrophys. J. 538, 628–637.CrossRefGoogle Scholar
Bret, A. 2015 Collisional behaviors of astrophysical collisionless plasmas. J. Plasma Phys. 81, 455810202.CrossRefGoogle Scholar
Bret, A. & Deutsch, C. 2005 Mixed two-stream filamentation modes in a collisional plasma. Phys. Plasmas 12, 082704.CrossRefGoogle Scholar
Bret, A., Gremillet, L., Benisti, D. & Lefebvre, E. 2008 Exact relativistic kinetic theory of an electron-beam-plasma system: hierarchy of the competing modes in the system-parameter space. Phys. Rev. Lett. 100, 205008.CrossRefGoogle ScholarPubMed
Bret, A., Gremillet, L. & Dieckmann, M. E. 2010 Multidimensional electron beam-plasma instabilities in the relativistic regime. Phys. Plasmas 17, 120501.CrossRefGoogle Scholar
Bret, A., Stockem, A., Fiuza, F., Ruyer, C., Gremillet, L., Narayan, R. & Silva, L. O. 2013 Collisionless shock formation, spontaneous electromagnetic fluctuations, and streaming instabilities. Phys. Plasmas 20, 042102.CrossRefGoogle Scholar
Bridle, A. H. & Perley, R. A. 1984 Extragalactic radio jets. Annu. Rev. Astron. Astrophys. 22, 319–358.CrossRefGoogle Scholar
Califano, F., Prandi, R., Pegoraro, F. & Bulanov, S. V. 1998 Nonlinear filamentation instability driven by an inhomogeneous current in a collisionless plasma. Phys. Rev. E 58, 7837–7845.Google Scholar
Chang, P., Spitkovsky, A. & Arons, J. 2008 Long-term evolution of magnetic turbulence in relativistic collisionless shocks: electron–positron plasmas. Astrophys. J. 674, 378–387.CrossRefGoogle Scholar
Dieckmann, M. E., Drury, L. O. & Shukla, P. K. 2006a On the ultrarelativistic two-stream instability, electrostatic turbulence and brownian motion. New J. Phys. 8, 40.CrossRefGoogle Scholar
Dieckmann, M. E., Frederiksen, J. T., Bret, A. & Shukla, P. K. 2006b Evolution of the fastest-growing relativistic mixed mode instability driven by a tenuous plasma beam in one and two dimensions. Phys. Plasmas 13, 112110.CrossRefGoogle Scholar
Dum, C. T. 1978 Anomalous heating by ion sound turbulence. Phys. Fluids 21, 945–955.CrossRefGoogle Scholar
Fabian, A. C. & Rees, M. J. 1979 Ss433-double jet in action. Mon. Not. R. Astron. Soc. 187, P13–P16.CrossRefGoogle Scholar
Gary, S. P. 1987 The electron electron acoustic instability. Phys. Fluids 30, 2745–2749.CrossRefGoogle Scholar
Haruki, T. & Sakai, J. I. 2003 Generation of magnetic field and electrostatic shock wave driven by counterstreaming pair plasmas. Phys. Plasmas 10, 392–397.CrossRefGoogle Scholar
Jaroschek, C. H., Lesch, H. & Treumann, R. A. 2004 Self-consistent diffusive lifetimes of weibel magnetic fields in gamma-ray bursts. Astrophys. J. 616, 1065–1071.CrossRefGoogle Scholar
Kaiser, C. R., Sunyaev, R. & Spruit, H. C. 2000 Internal shock model for microquasars. Astron. Astrophys. 356, 975–988.Google Scholar
Kazimura, Y., Sakai, J. I., Neubert, T. & Bulanov, S. V. 1998 Generation of a small-scale quasi-static magnetic field and fast particles during the collision of electron–positron plasma clouds. Astrophys. J. 498, L183–L186.CrossRefGoogle Scholar
Kono, M., Skoric, M. M. & ter Haar, D. 1980 Ponderomotive force in a dispersive medium in a variable electromagnetic-field. Phys. Rev. Lett. 45, 1629–1632.CrossRefGoogle Scholar
Kulkarni, S. R., Frail, D. A., Wieringa, M. H., Ekers, R. D., Sadler, E. M., Wark, R. M., Higdon, J. L., Phinney, E. S. & Bloom, J. S. 1998 Radio emission from the unusual supernova 1998bw and its association with the gamma-ray burst of 25 April 1998. Nature 395, 663–669.CrossRefGoogle Scholar
Landau, L. D. 1946 On the vibrations of the electronic plasma. J. Phys. (Moscow) 10, 25–34.Google Scholar
Marcowith, A., Bret, A., Bykov, A., Dieckmann, M. E., Drury, L. O., Lembege, B., Lemoine, M., Morlino, G., Murphy, G., Pelletier, G. et al. 2016 The microphysics of collisionless shock waves. Rep. Prog. Phys. 79, 046901.CrossRefGoogle ScholarPubMed
Margon, B. 1984 Observations of ss-433. Annu. Rev. Astron. Astrophys. 22, 507–536.CrossRefGoogle Scholar
Medvedev, M. V., Fiore, M., Fonseca, R. A., Silva, L. O. & Mori, W. B. 2005 Long-time evolution of magnetic fields in relativistic gamma-ray burst shocks. Astrophys. J. 618, L75–L78.CrossRefGoogle Scholar
Medvedev, M. V. & Loeb, A. 1999 Generation of magnetic fields in the relativistic shock of gamma-ray burst sources. Astrophys. J. 526, 697–706.CrossRefGoogle Scholar
Miller-Jones, J. C. A., McCormick, D. G., Fender, R. P., Spencer, R. E., Muxlow, T. W. B. & Pooley, G. G. 2005 Multiple relativistic outbursts of grs $1915+105$ : radio emission and internal shocks. Mon. Not. R. Astron. Soc. 363, 867–881.CrossRefGoogle Scholar
Milosavljevic, M. & Nakar, E. 2006 Weibel filament decay and thermalization in collisionless shocks and gamma-ray burst afterglows. Astrophys. J. 641, 978–983.CrossRefGoogle Scholar
Morse, R. L. & Nielson, C. W. 1969 One-, two- and three-dimensional numerical simulation of 2-beam plasmas. Phys. Rev. Lett. 23, 1087–1090.CrossRefGoogle Scholar
Morse, R. L. & Nielson, C. W. 1971 Numerical simulation of the weibel instability in one and two dimensions. Phys. Fluids 14, 830–840.CrossRefGoogle Scholar
O’Neil, T. M. 1965 Collisionless damping of nonlinear plasma oscillations. Phys. Fluids 8, 2255–2262.CrossRefGoogle Scholar
Oppenheim, M., Newman, D. L. & Goldman, M. V. 1999 Evolution of electron phase-space holes in a 2d magnetized plasma. Phys. Rev. Lett. 83, 2344–2347.CrossRefGoogle Scholar
Rees, M. J. 1978 M87 jet – internal shocks in a plasma beam. Mon. Not. R. Astron. Soc. 184, P61–P65.CrossRefGoogle Scholar
Sakai, J., Nakayama, T., Kazimura, Y. & Bulanov, S. 2000 Magnetic field generation and subsequent field dissipation with plasma heating in relativistic streaming pair plasmas. J. Phys. Soc. Japan 69, 2503–2513.CrossRefGoogle Scholar
Silva, L. O., Fonseca, R. A., Tonge, J. W., Dawson, J. M., Mori, W. B. & Medvedev, M. V. 2003 Interpenetrating plasma shells: near-equipartition magnetic field generation and nonthermal particle acceleration. Astrophys. J. 596, L121–L124.CrossRefGoogle Scholar
Silva, L. O., Fonseca, R. A., Tonge, J. W., Mori, W. B. & Dawson, J. M. 2002 On the role of the purely transverse weibel instability in fast ignitor scenarios. Phys. Plasmas 9, 2458–2461.CrossRefGoogle Scholar
Sironi, L. & Giannios, D. 2014 Relativistic pair beams from tev blazars: a source of reprocessed gev emission rather than intergalactic heating. Astrophys. J. 787, 49.CrossRefGoogle Scholar
Stockem, A., Dieckmann, M. E. & Schlickeiser, R. 2008 Suppression of the filamentation instability by a flow-aligned magnetic field: testing the analytic threshold with pic simulations. Plasma Phys. Control. Fusion 50, 025002.CrossRefGoogle Scholar
Stockem, A., Dieckmann, M. E. & Schlickeiser, R. 2009 Pic simulations of the thermal anisotropy-driven weibel instability: field growth and phase space evolution upon saturation. Plasma Phys. Control. Fusion 51, 075014.CrossRefGoogle Scholar
Stockem, A., Grismayer, T., Fonseca, R. A. & Silva, L. O. 2014 Electromagnetic field generation in the downstream of electrostatic shocks due to electron trapping. Phys. Rev. Lett. 113, 105002.CrossRefGoogle ScholarPubMed
Trigo, M. D., Miller-Jones, J. C. A., Migliari, S., Broderick, J. W. & Tzioumis, T. 2013 Baryons in the relativistic jets of the stellar-mass black-hole candidate 4u 1630-47. Nature 504, 260–262.CrossRefGoogle ScholarPubMed
Umeda, T., Omura, Y., Yoon, P. H., Gaelzer, R. & Matsumoto, H. 2003 Harmonic langmuir waves. iii. vlasov simulation. Phys. Plasmas 10, 382–391.CrossRefGoogle Scholar
Weibel, E. S. 1959 Spontaneously growing transverse waves in a plasma due to an anisotropic velocity distribution. Phys. Rev. Lett. 2, 83–84.CrossRefGoogle Scholar
Wharton, C. B., Malmberg, J. H. & O’Neil, T. M. 1968 Nonlinear effects of large-amplitude plasma waves. Phys. Fluids 11, 1761–1763.CrossRefGoogle Scholar
Woosley, S. E. & Bloom, J. S. 2006 The supernova-gamma-ray burst connection. Annu. Rev. Astron. Astrophys. 44, 507–556.CrossRefGoogle Scholar
Zel’Dovich, Ya. B., Raizer, Y. P., Probstein, R. F. & Hayes, W. D. 1967 Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena. Academic.Google Scholar
Supplementary material: File

Dieckmann and Bret supplementary material

Dieckmann and Bret supplementary material 1

Download Dieckmann and Bret supplementary material(File)
File 7.7 MB