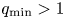1. Introduction
The kinetic effects of thermal ions can become more important for physics studies targeting fusion reactors, given the large ion temperature ($T_i > 10$![]() keV) and the presence of high-energy alpha particles. In recent DIII-D experiments, it was observed that thermal ions can drive both high-frequency chirping modes (Du et al. Reference Du, Hong, Heidbrink, Jian, Wang, Eidietis, Van Zeeland, Austin, Liu and Crocker2021) and beta-induced Alfvén-acoustic eigenmodes (BAAEs)/low-frequency Alfvén modes (Gorelenkov et al. Reference Gorelenkov, Van Zeeland, Berk, Crocker, Darrow, Fredrickson, Fu, Heidbrink, Menard and Nazikian2009; Choi et al. Reference Choi, Liu, Wei, Nicolau, Dong, Zhang, Lin, Heidbrink and Hahm2021; Ma et al. Reference Ma, Chen, Zonca, Li and Qiu2022). These modes can lead to degradation of plasma confinement or even minor disruption. It is therefore necessary to incorporate these effects in numerical simulation models for ITER and future reactors.
keV) and the presence of high-energy alpha particles. In recent DIII-D experiments, it was observed that thermal ions can drive both high-frequency chirping modes (Du et al. Reference Du, Hong, Heidbrink, Jian, Wang, Eidietis, Van Zeeland, Austin, Liu and Crocker2021) and beta-induced Alfvén-acoustic eigenmodes (BAAEs)/low-frequency Alfvén modes (Gorelenkov et al. Reference Gorelenkov, Van Zeeland, Berk, Crocker, Darrow, Fredrickson, Fu, Heidbrink, Menard and Nazikian2009; Choi et al. Reference Choi, Liu, Wei, Nicolau, Dong, Zhang, Lin, Heidbrink and Hahm2021; Ma et al. Reference Ma, Chen, Zonca, Li and Qiu2022). These modes can lead to degradation of plasma confinement or even minor disruption. It is therefore necessary to incorporate these effects in numerical simulation models for ITER and future reactors.
Although kinetic–magnetohydrodynamic models have been proposed before with thermal ions (Cheng & Johnson Reference Cheng and Johnson1999; Park et al. Reference Park, Belova, Fu, Tang, Strauss and Sugiyama1999), it is challenging to include the thermal ion kinetic effects in hybrid simulation models (Todo & Sato Reference Todo and Sato1998; Fu et al. Reference Fu, Park, Strauss, Breslau, Chen, Jardin and Sugiyama2006; Kim Reference Kim2008), which combine particle-in-cell (PIC) and magnetohydrodynamics (MHD) simulations. These models were developed for simulating the physics of enegetic particles (EPs) or fast ions, which come from neutral beam injection or ion cyclotron resonance heating (ICRH). The EPs can have a pressure or perpendicular current that is comparable to the thermal ions or electrons, but their density or momentum is often relatively small compared with the thermal ions. Their kinetic effects can then be included in the MHD framework through pressure or current coupling by adding corresponding terms in the momentum equation.
There are two major issues when extending this approach to thermal ions. First, since the MHD density and momentum equations are derived by taking moments of ion and electron kinetic equations, when thermal ion kinetic equations are calculated separately, these MHD equations become redundant and the error between the two approaches can lead to numerical issues or even parasitic modes. Second, as ions and electrons are calculated separately (one as kinetic particles and one as a fluid component), the parallel electric force between them must be calculated as a connection, which is often missing in ideal MHD calculations or treated as a high-order two-fluid effect. These issues can be mitigated by using a fully implicit or predictor–corrector method for particle pushing and MHD equation calculation (Barnes, Cheng & Parker Reference Barnes, Cheng and Parker2008), with a cost of computation time.
In this paper, we describe a new kinetic–MHD coupling scheme, which is similar to the one used in the MEGA code for studying thermal ion kinetic effects in Large Helical Device (LHD) plasmas (Sato & Todo Reference Sato and Todo2019, Reference Sato and Todo2020). In this scheme, in addition to the coupling terms in the MHD momentum equation, we have two more equations to connect the MHD and kinetic parts. One is the synchronization of the parallel velocity between the kinetic ions and the MHD, and the other is the synchronization of ion density. These two new equations are introduced to ensure quasineutrality and to avoid parasitic modes.
In this kinetic–MHD model, all the ions, including the thermal ones and the fast ones, are modelled as kinetic particles using the PIC method. The MHD equation is in charge of calculating the evolution of fields and the electron pressure and temperature. The parallel electric field caused by separation of electrons and ions is also added in the ion kinetic equations. This scheme is implemented in the kinetic–MHD code M3D-C1-K (Liu et al. Reference Liu, Jardin, Qin, Xiao, Ferraro and Breslau2022), which is based on the finite-element MHD code M3D-C1 (Ferraro & Jardin Reference Ferraro and Jardin2009; Jardin et al. Reference Jardin, Ferraro, Breslau and Chen2012). It is found that the semi-implicit method introduced for solving the MHD equations (Jardin et al. Reference Jardin, Ferraro, Breslau and Chen2012) is helpful for stabilizing numerical instabilities after including ion kinetic terms, and the simulation can run with large timesteps to save computation time.
Using this new model, we investigate the kinetic effects of thermal ions, especially Landau damping, in kinetic MHD simulations. We first tested the new simulation model in an ion acoustic wave (IAW) simulation, and achieved good agreement of mode frequency and damping rate with the theory. We then studied $n=1$![]() (n is the toroidal mode number) fishbone modes using DIII-D and NSTX equilibrium with $q_\mathrm {min}$
(n is the toroidal mode number) fishbone modes using DIII-D and NSTX equilibrium with $q_\mathrm {min}$![]() (the minimum safety factor) slightly larger than 1. This fishbone mode, which is connected to the non-resonant (1,1) kink mode, has been studied before using kinetic–MHD simulation without thermal ion kinetic effects (Brennan, Kim & Haye Reference Brennan, Kim and Haye2012; Wang et al. Reference Wang, Fu, Breslau and Liu2013; Shen et al. Reference Shen, Wang, Fu, Xu, Li and Liu2017, Reference Shen, Wang, Fu, Xu and Ren2020).
(the minimum safety factor) slightly larger than 1. This fishbone mode, which is connected to the non-resonant (1,1) kink mode, has been studied before using kinetic–MHD simulation without thermal ion kinetic effects (Brennan, Kim & Haye Reference Brennan, Kim and Haye2012; Wang et al. Reference Wang, Fu, Breslau and Liu2013; Shen et al. Reference Shen, Wang, Fu, Xu, Li and Liu2017, Reference Shen, Wang, Fu, Xu and Ren2020).
We find that, for simulation with only fast ions treated kinetically, the dominant $n=1$![]() mode has a transition from a classical fishbone mode to a Alfvén eigenmode (AE) like mode as $q_\mathrm {min}$
mode has a transition from a classical fishbone mode to a Alfvén eigenmode (AE) like mode as $q_\mathrm {min}$![]() increases, with a significant increase of mode frequency, which is consistent with the NIMROD simulation results (Brennan et al. Reference Brennan, Kim and Haye2012). After adding a kinetic treatment of the thermal ions, the frequencies of the fishbone modes increase and the growth rates decrease. The AE-like mode branch becomes stable. These simulation results indicate that both of the two modes are strongly affected by the Landau damping effect from thermal ions, which was not considered in previous kinetic–MHD simulations. In addition, we undertook a nonlinear simulation for the fishbone mode to study the mode saturation and the effects on particle transport.
increases, with a significant increase of mode frequency, which is consistent with the NIMROD simulation results (Brennan et al. Reference Brennan, Kim and Haye2012). After adding a kinetic treatment of the thermal ions, the frequencies of the fishbone modes increase and the growth rates decrease. The AE-like mode branch becomes stable. These simulation results indicate that both of the two modes are strongly affected by the Landau damping effect from thermal ions, which was not considered in previous kinetic–MHD simulations. In addition, we undertook a nonlinear simulation for the fishbone mode to study the mode saturation and the effects on particle transport.
The paper is organized as follows. In § 2 we discuss the kinetic–MHD coupling scheme including the thermal ions, with density and parallel velocity synchronization. In § 3 we present the simulation results of IAWs using the new scheme, and compare the Landau damping rates with theoretical results. In § 4 we show the numerical simulation of $n=1$![]() fishbone modes in a DIII-D equilibrium without and with the thermal ion kinetic effects. In § 5 we describe similar simulations in NSTX scenarios, using a more realistic EP distribution. In § 6 we show the results of a nonlinear simulation of fishbones in NSTX, focusing on the mode saturation behaviour. Finally, the summary is given in § 7.
fishbone modes in a DIII-D equilibrium without and with the thermal ion kinetic effects. In § 5 we describe similar simulations in NSTX scenarios, using a more realistic EP distribution. In § 6 we show the results of a nonlinear simulation of fishbones in NSTX, focusing on the mode saturation behaviour. Finally, the summary is given in § 7.
2. Kinetic–MHD model with thermal ion kinetic effects
In this section we present the kinetic–MHD model implemented in the M3D-C1-K code. The code was initially developed as a kinetic module for the extended MHD code M3D-C1 (Jardin et al. Reference Jardin, Ferraro, Breslau and Chen2012) using a pressure coupling scheme, which is similar to other kinetic–MHD codes like M3D-K (Fu et al. Reference Fu, Park, Strauss, Breslau, Chen, Jardin and Sugiyama2006) and NIMROD (Kim Reference Kim2008). The particle equation of motion, particle weight equations and coupling scheme are described in Liu et al. (Reference Liu, Jardin, Qin, Xiao, Ferraro and Breslau2022). In the new version of M3D-C1-K, we treat both the thermal ions and fast ions as kinetic particles and calculate their dynamics using the PIC method, and electrons are treated using a fluid model. The MHD equations with kinetic coupling are as follows:

Here, $\rho$![]() is the total ion mass density, $\boldsymbol {v}_\parallel$
is the total ion mass density, $\boldsymbol {v}_\parallel$![]() and $\boldsymbol {v}_\perp$
and $\boldsymbol {v}_\perp$![]() are the MHD velocity parallel and perpendicular to the magnetic field $\boldsymbol {B}$
are the MHD velocity parallel and perpendicular to the magnetic field $\boldsymbol {B}$![]() , $\boldsymbol {J}$
, $\boldsymbol {J}$![]() is the plasma current density, $\boldsymbol {E}$
is the plasma current density, $\boldsymbol {E}$![]() is the electric field, $\nu$
is the electric field, $\nu$![]() and $\eta$
and $\eta$![]() are the viscosity and resistivity coefficients, $\boldsymbol {P}_\parallel$
are the viscosity and resistivity coefficients, $\boldsymbol {P}_\parallel$![]() and $\boldsymbol {P}_\perp$
and $\boldsymbol {P}_\perp$![]() are the parallel and perpendicular components of the ion pressure tensor and the subscripts $i$
are the parallel and perpendicular components of the ion pressure tensor and the subscripts $i$![]() and $f$
and $f$![]() represent thermal ions and fast ions. The electron pressure $p_e$
represent thermal ions and fast ions. The electron pressure $p_e$![]() can either be calculated with the convection and diffusion terms
can either be calculated with the convection and diffusion terms
or as a product of density and electron temperature ($p_e=n_eT_e$![]() ). The temperature can be calculated separately
). The temperature can be calculated separately
where $\gamma _e$![]() is the electron specific heat ratio and $\kappa _\parallel$
is the electron specific heat ratio and $\kappa _\parallel$![]() and $\kappa _\perp$
and $\kappa _\perp$![]() are the parallel and perpendicular heat transport coefficients.
are the parallel and perpendicular heat transport coefficients.
The kinetic ion orbit follows the guiding-centre equation of motion
where
Here, $\boldsymbol {X}$![]() is the particle guiding-centre location, $V_\parallel$
is the particle guiding-centre location, $V_\parallel$![]() the particle parallel velocity, $m$
the particle parallel velocity, $m$![]() is the ion mass, $\mu =mV_\perp ^2/2B$
is the ion mass, $\mu =mV_\perp ^2/2B$![]() is the magnetic moment and $\boldsymbol {b}=\boldsymbol {B}/B$
is the magnetic moment and $\boldsymbol {b}=\boldsymbol {B}/B$![]() . Note that the electric field $\boldsymbol {E}^\star$
. Note that the electric field $\boldsymbol {E}^\star$![]() has an additional term in the parallel direction, $-\boldsymbol {\nabla }_\parallel p_e/n_e e$
has an additional term in the parallel direction, $-\boldsymbol {\nabla }_\parallel p_e/n_e e$![]() . This term is obtained by ignoring the inertial term in the electron momentum equation in the parallel direction.
. This term is obtained by ignoring the inertial term in the electron momentum equation in the parallel direction.
Assuming that the ion distribution is given as a function of location $\boldsymbol {X}$![]() , energy $\mathcal {E}=(1/2)mV^2$
, energy $\mathcal {E}=(1/2)mV^2$![]() and pitch angle $\xi =V_\parallel /V$
and pitch angle $\xi =V_\parallel /V$![]() , the weight equation for $\delta f$
, the weight equation for $\delta f$![]() calculation is obtained from drift kinetic equations
calculation is obtained from drift kinetic equations
where

and $\alpha =1$![]() for linear calculations and $\alpha =1-w$
for linear calculations and $\alpha =1-w$![]() for nonlinear calculations. Alternatively, one can calculate the difference between the results of the equations of motion with equilibrium and perturbed fields to obtain these $(\cdots )_1$
for nonlinear calculations. Alternatively, one can calculate the difference between the results of the equations of motion with equilibrium and perturbed fields to obtain these $(\cdots )_1$![]() terms.
terms.
Finally, the density, parallel velocity and pressure for thermal (subscript $i$![]() ) and fast (subscript $f$
) and fast (subscript $f$![]() ) ions used in the MHD equations are calculated from particle deposition on fields
) ions used in the MHD equations are calculated from particle deposition on fields




Here, $S$![]() is the particle shape function, $k_{i,f}$
is the particle shape function, $k_{i,f}$![]() are indices of particles, $m_i$
are indices of particles, $m_i$![]() and $m_f$
and $m_f$![]() are the ion mass, $Z_i$
are the ion mass, $Z_i$![]() and $Z_f$
and $Z_f$![]() are ion effective charge, and $v_{\parallel 0}$
are ion effective charge, and $v_{\parallel 0}$![]() is the parallel velocity of the ion equilibrium distribution $f_0$
is the parallel velocity of the ion equilibrium distribution $f_0$![]() . The details of the implementation of the particle deposition calculation can be found in Liu et al. (Reference Liu, Jardin, Qin, Xiao, Ferraro and Breslau2022). For simulations with finite Larmor radius (FLR) effects, both the field evaluation and the particle deposition need to take into account average along the gyro-orbit.
. The details of the implementation of the particle deposition calculation can be found in Liu et al. (Reference Liu, Jardin, Qin, Xiao, Ferraro and Breslau2022). For simulations with finite Larmor radius (FLR) effects, both the field evaluation and the particle deposition need to take into account average along the gyro-orbit.
The kinetic–MHD scheme here is similar to that implemented in MEGA (Sato & Todo Reference Sato and Todo2019, Reference Sato and Todo2020), except that we use pressure coupling while MEGA uses current coupling. As pointed out in Liu et al. (Reference Liu, Jardin, Qin, Xiao, Ferraro and Breslau2022), the two kinds of coupling schemes are equivalent for calculating $v_\perp$![]() . Comparing with the pressure coupling scheme with thermal ions in Park et al. (Reference Park, Belova, Fu, Tang, Strauss and Sugiyama1999), we have additional equations for synchronization of the ion density and parallel velocity with MHD fields, whereas in Park et al. (Reference Park, Belova, Fu, Tang, Strauss and Sugiyama1999) these quantities are calculated by the MHD equations. For example, the parallel velocity is solved as
. Comparing with the pressure coupling scheme with thermal ions in Park et al. (Reference Park, Belova, Fu, Tang, Strauss and Sugiyama1999), we have additional equations for synchronization of the ion density and parallel velocity with MHD fields, whereas in Park et al. (Reference Park, Belova, Fu, Tang, Strauss and Sugiyama1999) these quantities are calculated by the MHD equations. For example, the parallel velocity is solved as

If assuming small ion energy and ignoring the gradient and curvature drifts, one can verify that (2.23) can be obtained by taking the moment of the kinetic equations. Here, $\boldsymbol {\nabla }_\parallel p_e$![]() is derived from the parallel electric field term in (2.11), which is used in particle weight equations. In principle, the pressure coupling scheme in Park et al. (Reference Park, Belova, Fu, Tang, Strauss and Sugiyama1999) is equivalent to our coupling scheme and the simulation results should agree with each other, although the calculations of the ion density and $v_\parallel$
is derived from the parallel electric field term in (2.11), which is used in particle weight equations. In principle, the pressure coupling scheme in Park et al. (Reference Park, Belova, Fu, Tang, Strauss and Sugiyama1999) is equivalent to our coupling scheme and the simulation results should agree with each other, although the calculations of the ion density and $v_\parallel$![]() in the MHD equations are redundant.
in the MHD equations are redundant.
However, we find that, in M3D-C1, due to the fact that the fluid equations and kinetic equations are solved subsequently in one timestep, in the simulation using the scheme of Park et al. (Reference Park, Belova, Fu, Tang, Strauss and Sugiyama1999), the difference between $\delta n$![]() and $\delta v_\parallel$
and $\delta v_\parallel$![]() from the fluid and kinetic equations can increase with time, which violates the quasineutrality condition and leads to parasitic modes that overwhelm the numerical result. We thus replace the two MHD equations with the synchronization schemes instead to avoid these issues. The perpendicular momentum equation (2.1) of MHD is kept as it provides additional information for kinetic simulation. In fact, (2.1) can be regarded as a decomposition of the plasma perpendicular current, in which the $\rho \partial \boldsymbol {v}_\perp /\partial t$
from the fluid and kinetic equations can increase with time, which violates the quasineutrality condition and leads to parasitic modes that overwhelm the numerical result. We thus replace the two MHD equations with the synchronization schemes instead to avoid these issues. The perpendicular momentum equation (2.1) of MHD is kept as it provides additional information for kinetic simulation. In fact, (2.1) can be regarded as a decomposition of the plasma perpendicular current, in which the $\rho \partial \boldsymbol {v}_\perp /\partial t$![]() term represents the polarization current, and the pressure terms represent the drift and magnetization current.
term represents the polarization current, and the pressure terms represent the drift and magnetization current.
The ions’ parallel velocity is used in the electron pressure (2.5) and temperature equation (2.6), assuming that the electrons and ions are moving together. However, when considering two-fluid effects, there is a difference between the electron and ion velocities due to the parallel current. This difference can lead to correction terms in (2.5) and (2.6) that are proportional to $d_i/L$![]() ($d_i$
($d_i$![]() is the ion skin depth), and thus can be considered as a two-fluid term. These two-fluid terms are ignored in the current simulation model as we are dealing with long-wavelength modes. The additional parallel electric field used in (2.11) is not included in Ohm's law (2.4) for the same reason. These two-fluid effects can be important for small-wavelengh modes like kinetic Alfvén waves (KAWs), and will be studied in future.
is the ion skin depth), and thus can be considered as a two-fluid term. These two-fluid terms are ignored in the current simulation model as we are dealing with long-wavelength modes. The additional parallel electric field used in (2.11) is not included in Ohm's law (2.4) for the same reason. These two-fluid effects can be important for small-wavelengh modes like kinetic Alfvén waves (KAWs), and will be studied in future.
3. Numerical simulation of IAWs
In this section we test the new version of M3D-C1-K in an IAW simulation. The oscillation of IAWs can be easily simulated using a MHD code. However, for $T_i \sim T_e$![]() , IAWs will be strongly damped due to parallel Landau damping, which can only be simulated by including the kinetic effects of thermal ions.
, IAWs will be strongly damped due to parallel Landau damping, which can only be simulated by including the kinetic effects of thermal ions.
In the simulation we treat thermal ions as kinetic particles and electrons as a fluid component. Since IAW is an electrostatic mode, we only keep the MHD equation (2.5) and ignore the $v_\perp$![]() terms. The MHD equation and the particle equation of motion are limited to being one-dimensional along the wave vector. For the electron pressure we choose the electron heat capacity ratio $\gamma _e=1$
terms. The MHD equation and the particle equation of motion are limited to being one-dimensional along the wave vector. For the electron pressure we choose the electron heat capacity ratio $\gamma _e=1$![]() assuming they are isothermal. The parallel velocity is initialized like a sinusoidal function with a fixed wavenumber $k$
assuming they are isothermal. The parallel velocity is initialized like a sinusoidal function with a fixed wavenumber $k$![]() , which can drive perturbations on $p_e$
, which can drive perturbations on $p_e$![]() and $p_i$
and $p_i$![]() and lead to a standing wave. The electron and ion densities are the same assuming $Z_{\mathrm {eff}}=1$
and lead to a standing wave. The electron and ion densities are the same assuming $Z_{\mathrm {eff}}=1$![]() , and the ion temperature is set to be a fraction of the electron temperature.
, and the ion temperature is set to be a fraction of the electron temperature.
For MHD-only simulation, we find that IAW gives oscillations of $\delta p$![]() and $\delta v_\parallel$
and $\delta v_\parallel$![]() with little damping. With ion kinetic effects, the oscillation experiences damping, as shown in figure 1. We find that the mode damping rate is consistent with the theoretical Landau damping rate of IAW, which is shown as the red line. Note that, for $T_i/T_e>0.1$
with little damping. With ion kinetic effects, the oscillation experiences damping, as shown in figure 1. We find that the mode damping rate is consistent with the theoretical Landau damping rate of IAW, which is shown as the red line. Note that, for $T_i/T_e>0.1$![]() , the Landau damping rates $\gamma _{{\rm LD}}$
, the Landau damping rates $\gamma _{{\rm LD}}$![]() of IAWs become comparable to $\omega$
of IAWs become comparable to $\omega$![]() and the perturbative calculation is not accurate. In these cases $\gamma _{{\rm LD}}$
and the perturbative calculation is not accurate. In these cases $\gamma _{{\rm LD}}$![]() should be solved numerically from the plasma dispersion function $Z(\zeta )$
should be solved numerically from the plasma dispersion function $Z(\zeta )$![]() . Here, we use the empirical formula from Chen (Reference Chen2013) to obtain the frequencies and the Landau damping rates of IAWs for $0.1< T_i/T_e<1$
. Here, we use the empirical formula from Chen (Reference Chen2013) to obtain the frequencies and the Landau damping rates of IAWs for $0.1< T_i/T_e<1$![]()

where $\omega _0=k\sqrt {k_B T_e/m_i}$![]() and $k_B$
and $k_B$![]() is the Boltzmann constant. Equation (3.1) is calculated by assuming the ion heat capacity ratio $\gamma _i=3$
is the Boltzmann constant. Equation (3.1) is calculated by assuming the ion heat capacity ratio $\gamma _i=3$![]() since they only suffer one-dimensional compression (McKinstrie, Giacone & Startsev Reference McKinstrie, Giacone and Startsev1999; Chen Reference Chen2013).
since they only suffer one-dimensional compression (McKinstrie, Giacone & Startsev Reference McKinstrie, Giacone and Startsev1999; Chen Reference Chen2013).

Figure 1. Blue line is the time signal of $\delta p_e$![]() from IAW simulation with $T_i=0.2 T_e$
from IAW simulation with $T_i=0.2 T_e$![]() . Red line shows a mode damping trend with a rate calculated from (3.2). The time unit $\tau _0=1/\omega _0$
. Red line shows a mode damping trend with a rate calculated from (3.2). The time unit $\tau _0=1/\omega _0$![]() .
.
Figure 2 shows the results of IAW frequencies and damping rates from the M3D-C1-K simulation for different values of $T_i/T_e$![]() . For small $T_i/T_e$
. For small $T_i/T_e$![]() , the damping rate is zero and the frequency is close to the MHD-only result $\omega _0$
, the damping rate is zero and the frequency is close to the MHD-only result $\omega _0$![]() . For $T_i/T_e>0.3$
. For $T_i/T_e>0.3$![]() , the damping rate becomes comparable to the frequency, indicating IAWs are strongly damped. Both $\omega$
, the damping rate becomes comparable to the frequency, indicating IAWs are strongly damped. Both $\omega$![]() and $\gamma _{{\rm LD}}$
and $\gamma _{{\rm LD}}$![]() are close to the theoretical results, indicating that the new kinetic–MHD model successfully captures the Landau damping physics.
are close to the theoretical results, indicating that the new kinetic–MHD model successfully captures the Landau damping physics.
We find that, for large $T_i/T_e$![]() , the mode can have echoes after being significantly damped, as shown in figure 3. This phenomenon is a typical nonlinear behaviour for the Landau damped mode, which is different from dissipative damping (Kadomtsev Reference Kadomtsev1968). This effect indicates that, although the mode is damped due to phase mixing, the particles still retain some ‘memory’ of the preceding oscillation, which can be reflected as echoes at later times.
, the mode can have echoes after being significantly damped, as shown in figure 3. This phenomenon is a typical nonlinear behaviour for the Landau damped mode, which is different from dissipative damping (Kadomtsev Reference Kadomtsev1968). This effect indicates that, although the mode is damped due to phase mixing, the particles still retain some ‘memory’ of the preceding oscillation, which can be reflected as echoes at later times.

Figure 3. Time evolution of $\delta p_e$![]() from IAW simulation with $T_i=0.3 T_e$
from IAW simulation with $T_i=0.3 T_e$![]() , showing echoes of oscillation after the mode is damped.
, showing echoes of oscillation after the mode is damped.
4. Linear simulation of fishbone modes in DIII-D
In this section we discuss the linear $n=1$![]() fishbone mode simulation using M3D-C1-K without and with thermal ion kinetic effects. We use an equilibrium from the DIII-D tokamak experiment, obtained from hybrid discharge #125476, which has been studied before for $n=1$
fishbone mode simulation using M3D-C1-K without and with thermal ion kinetic effects. We use an equilibrium from the DIII-D tokamak experiment, obtained from hybrid discharge #125476, which has been studied before for $n=1$![]() MHD instabilities using NIMROD (Brennan et al. Reference Brennan, Kim and Haye2012). In the experiment, both a (1,1) kink mode and (2,1) and (3,2) tearing modes are present (La Haye et al. Reference La Haye, Brennan, Buttery and Gerhardt2010). We use a single equilibrium reconstruction from the EFIT code (Lao et al. Reference Lao, Ferron, Groebner, Howl, John, Strait and Taylor1990) including motional Stark effect profile data, by choosing a time (3425 ms) during the stationary phase of the discharge with benign tearing mode excitation. Toroidal flow is not included in the simulation. The equilibrium profiles of $q$
MHD instabilities using NIMROD (Brennan et al. Reference Brennan, Kim and Haye2012). In the experiment, both a (1,1) kink mode and (2,1) and (3,2) tearing modes are present (La Haye et al. Reference La Haye, Brennan, Buttery and Gerhardt2010). We use a single equilibrium reconstruction from the EFIT code (Lao et al. Reference Lao, Ferron, Groebner, Howl, John, Strait and Taylor1990) including motional Stark effect profile data, by choosing a time (3425 ms) during the stationary phase of the discharge with benign tearing mode excitation. Toroidal flow is not included in the simulation. The equilibrium profiles of $q$![]() and total pressure, and the shape of flux contours, are shown in figure 4. For this equilibrium the safety factor has a minimum $q_\mathrm {min}=1.06$
and total pressure, and the shape of flux contours, are shown in figure 4. For this equilibrium the safety factor has a minimum $q_\mathrm {min}=1.06$![]() located at $\psi /\psi _0=0.0625$
located at $\psi /\psi _0=0.0625$![]() , inside which there is a slightly reverse shear near the core. To study the effect of the $q$
, inside which there is a slightly reverse shear near the core. To study the effect of the $q$![]() profile on the stability of fishbone modes, we apply the Bateman scaling method (Bateman Reference Bateman1978) to the equilibrium, which means that we add a constant value to $F^2$
profile on the stability of fishbone modes, we apply the Bateman scaling method (Bateman Reference Bateman1978) to the equilibrium, which means that we add a constant value to $F^2$![]() ($F=RB_\phi$
($F=RB_\phi$![]() ) to change the toroidal field while keeping the pressure and the toroidal current fixed and the Grad–Shafranov equation satisfied.
) to change the toroidal field while keeping the pressure and the toroidal current fixed and the Grad–Shafranov equation satisfied.

Figure 4. (a) Profiles of $q$![]() and total pressure of the equilibrium used in the DIII-D simulation. (b) Flux contours and mesh boundary used in the simulation.
and total pressure of the equilibrium used in the DIII-D simulation. (b) Flux contours and mesh boundary used in the simulation.
Both thermal ions and fast ions from neutral beam injection are included in the kinetic–MHD simulation. Both of the populations are deuterium. The thermal ions are initialized with a Maxwellian distribution, with density $n_i=n_e-n_f$![]() ($n_f$
($n_f$![]() is the fast ion density) and temperature $T_i=T_e$
is the fast ion density) and temperature $T_i=T_e$![]() . The fast ions have a slowing-down distribution in energy with an isotropic distribution in pitch angle
. The fast ions have a slowing-down distribution in energy with an isotropic distribution in pitch angle
where $\mathcal {E}_c=10$![]() keV is the critical energy; $f_0$
keV is the critical energy; $f_0$![]() has a cutoff energy $\mathcal {E}_\mathrm {max}=50$
has a cutoff energy $\mathcal {E}_\mathrm {max}=50$![]() keV. Both $\mathcal {E}_c$
keV. Both $\mathcal {E}_c$![]() and $\mathcal {E}_\mathrm {max}$
and $\mathcal {E}_\mathrm {max}$![]() are constants in the simulation domain. The density of the fast ions $n_f$
are constants in the simulation domain. The density of the fast ions $n_f$![]() has the same profile as the total pressure, so that the fraction of fast ion pressure to the total pressure is fixed (16 %) at different flux surfaces.
has the same profile as the total pressure, so that the fraction of fast ion pressure to the total pressure is fixed (16 %) at different flux surfaces.
For linear simulations, we use a two-dimensional finite element mesh and a spectral representation of the MHD fields in the toroidal direction. The two-dimensional unstructured mesh has 5495 triangular elements which are uniformly distributed. For the kinetic–MHD simulation we use $8\times 10^6$![]() particle markers, half of which are for the simulation of fast ions and the other half for the thermal ions.
particle markers, half of which are for the simulation of fast ions and the other half for the thermal ions.
The simulation results of mode growth rates and frequencies are summarized in figure 5, with $q_\mathrm {min}$![]() varying from 1.0 to 1.2. The MHD-only result (blue line) shows that the $n=1$
varying from 1.0 to 1.2. The MHD-only result (blue line) shows that the $n=1$![]() kink mode is unstable for $q_\mathrm {min}<1.06$
kink mode is unstable for $q_\mathrm {min}<1.06$![]() . After including the fast ion kinetic effects (red lines), the mode growth rates decrease for $q_\mathrm {min}<1.04$
. After including the fast ion kinetic effects (red lines), the mode growth rates decrease for $q_\mathrm {min}<1.04$![]() , and the modes have finite frequencies due to the wave–particle resonances, which increase with $q_\mathrm {min}$
, and the modes have finite frequencies due to the wave–particle resonances, which increase with $q_\mathrm {min}$![]() . For $q_\mathrm {min}>1.1$
. For $q_\mathrm {min}>1.1$![]() , there is still a weakly unstable $n=1$
, there is still a weakly unstable $n=1$![]() mode which is driven by fast ions, with frequencies significantly larger than those of the $q_\mathrm {min}<1.06$
mode which is driven by fast ions, with frequencies significantly larger than those of the $q_\mathrm {min}<1.06$![]() cases. The manifest change of frequencies indicates that the dominant $n=1$
cases. The manifest change of frequencies indicates that the dominant $n=1$![]() mode changes from a fishbone-like branch to a AE-like branch with distinct frequencies. This mode can be beta-induced Alfvén eigenmode (BAE) or BAAE, and is coupled with the reversed shear Alfvén eigenmode (RSAE) given the reversed shear of $q$
mode changes from a fishbone-like branch to a AE-like branch with distinct frequencies. This mode can be beta-induced Alfvén eigenmode (BAE) or BAAE, and is coupled with the reversed shear Alfvén eigenmode (RSAE) given the reversed shear of $q$![]() profile near the core. The results of the mode frequencies and growth rates are close to the NIMROD results in Brennan et al. (Reference Brennan, Kim and Haye2012), except that the growth rate for $q_\mathrm {min}>1.1$
profile near the core. The results of the mode frequencies and growth rates are close to the NIMROD results in Brennan et al. (Reference Brennan, Kim and Haye2012), except that the growth rate for $q_\mathrm {min}>1.1$![]() keeps dropping to zero as $q_\mathrm {min}$
keeps dropping to zero as $q_\mathrm {min}$![]() increases, whereas in Brennan et al. (Reference Brennan, Kim and Haye2012) the growth rate is almost a constant for large $q_\mathrm {min}$
increases, whereas in Brennan et al. (Reference Brennan, Kim and Haye2012) the growth rate is almost a constant for large $q_\mathrm {min}$![]() .
.

Figure 5. Growth rates (solid lines) and frequencies (dashed lines) as functions of $q_\mathrm {min}$![]() of the $n=1$
of the $n=1$![]() mode from M3D-C1 linear simulations with DIII-D equilibrium. The blue line shows the MHD-only result. The red lines show the kinetic–MHD results with only fast ions. The green lines show the results with both thermal and energetic ions.
mode from M3D-C1 linear simulations with DIII-D equilibrium. The blue line shows the MHD-only result. The red lines show the kinetic–MHD results with only fast ions. The green lines show the results with both thermal and energetic ions.
The mode growth rates and frequencies including both fast ions and thermal ions are shown as green lines in figure 5. For the low-frequency fishbone-like branch, there is a significant drop of the mode growth rate compared with the results with only fast ions, and an increase of the mode frequency. It is known that the fishbone mode is driven by the trapped ions which can have resonances with the mode through precession motion. Therefore, the kinetic effects of thermal trapped ions can provide additional drive of the fishbone mode rotation and raise the mode frequency. On the other hand, the precession motion of trapped ions can weaken their response to the MHD mode and thus lower the mode growth rate (Sato & Todo Reference Sato and Todo2019). In addition, the parallel electric field is only turned on in these thermal ion simulations, and the Landau damping can further stabilize the modes.
The two-dimensional structure of the fishbone mode for $q_\mathrm {min}=1.04$![]() including thermal ions is summarized in figures 6–9. Figure 6 shows the mode structure of the perturbed velocity streamfunction ($\delta \phi$
including thermal ions is summarized in figures 6–9. Figure 6 shows the mode structure of the perturbed velocity streamfunction ($\delta \phi$![]() ) and magnetic flux ($\delta \psi$
) and magnetic flux ($\delta \psi$![]() ). Here, $\delta \phi$
). Here, $\delta \phi$![]() is dominated by $m=1$
is dominated by $m=1$![]() near the core and $m=2$
near the core and $m=2$![]() at the outer region, and $\delta \psi$
at the outer region, and $\delta \psi$![]() is dominated by $m=2$
is dominated by $m=2$![]() . Figure 7 shows the structure of the electron and ion pressures, which is similar to the $\delta \phi$
. Figure 7 shows the structure of the electron and ion pressures, which is similar to the $\delta \phi$![]() structure. The similarity between $\delta p_e$
structure. The similarity between $\delta p_e$![]() and $\delta p_i$
and $\delta p_i$![]() indicates that the quasineutrality condition is satisfied. Figure 8 shows the structure of the fast ion pressure, including parallel and perpendicular components in (2.21) and (2.22). The non-adiabatic response ($\delta p_\perp -\delta p_\parallel$
indicates that the quasineutrality condition is satisfied. Figure 8 shows the structure of the fast ion pressure, including parallel and perpendicular components in (2.21) and (2.22). The non-adiabatic response ($\delta p_\perp -\delta p_\parallel$![]() ) is mostly located in the low-field side, as it comes from the resonant trapped particles (Fu et al. Reference Fu, Park, Strauss, Breslau, Chen, Jardin and Sugiyama2006; Kim Reference Kim2008; Liu et al. Reference Liu, Jardin, Qin, Xiao, Ferraro and Breslau2022). Figure 9 shows the comparison of $\delta v_\parallel$
) is mostly located in the low-field side, as it comes from the resonant trapped particles (Fu et al. Reference Fu, Park, Strauss, Breslau, Chen, Jardin and Sugiyama2006; Kim Reference Kim2008; Liu et al. Reference Liu, Jardin, Qin, Xiao, Ferraro and Breslau2022). Figure 9 shows the comparison of $\delta v_\parallel$![]() from the kinetic–MHD simulation using parallel velocity synchronization (2.20), with the result of the simulation with only fast ions and no synchronization. The two results are close and both are dominated by $m=2$
from the kinetic–MHD simulation using parallel velocity synchronization (2.20), with the result of the simulation with only fast ions and no synchronization. The two results are close and both are dominated by $m=2$![]() , showing that the kinetic equations successfully capture the parallel dynamics of the MHD system.
, showing that the kinetic equations successfully capture the parallel dynamics of the MHD system.

Figure 6. Two-dimensional structure of $\delta \phi$![]() (a) and $\delta \psi$
(a) and $\delta \psi$![]() (b) from DIII-D $n=1$
(b) from DIII-D $n=1$![]() linear simulation of the $q_\mathrm {min}=1.04$
linear simulation of the $q_\mathrm {min}=1.04$![]() case with thermal ions.
case with thermal ions.

Figure 7. Two-dimensional structure of perturbed electron pressure $\delta p_e$![]() (a) and thermal ion pressure $\delta p_i$
(a) and thermal ion pressure $\delta p_i$![]() (b) from the linear simulation of the $q_\mathrm {min}=1.04$
(b) from the linear simulation of the $q_\mathrm {min}=1.04$![]() case with thermal ions.
case with thermal ions.

Figure 8. Two-dimensional structure of perpendicular (a) and parallel (b) fast ion pressure from the linear simulation of the $q_\mathrm {min}=1.04$![]() case with thermal ions, and the difference between the two (c).
case with thermal ions, and the difference between the two (c).
According to the simulation results, we find that both the fishbone branch and the AE-like branch of the $n=1$![]() mode are susceptible to Landau damping of thermal ions. The parallel wavenumber can be estimated as follows:
mode are susceptible to Landau damping of thermal ions. The parallel wavenumber can be estimated as follows:
Using the mode frequency obtained from the simulation with fast ions and $m=1$![]() , for $q_\mathrm {min}=1.04$
, for $q_\mathrm {min}=1.04$![]() we have $\omega /k_\parallel =2.3 v_\mathrm {th}$
we have $\omega /k_\parallel =2.3 v_\mathrm {th}$![]() , and for $q_\mathrm {min}=1.15$
, and for $q_\mathrm {min}=1.15$![]() we have $\omega /k_\parallel =2.68 v_\mathrm {th}$
we have $\omega /k_\parallel =2.68 v_\mathrm {th}$![]() , where $v_\mathrm {th}=\sqrt {T_i/m_i}$
, where $v_\mathrm {th}=\sqrt {T_i/m_i}$![]() . Therefore, the Landau damping effects are important for both branches, which explains the stabilization of the mode by thermal ions for the $q_\mathrm {min}>1.06$
. Therefore, the Landau damping effects are important for both branches, which explains the stabilization of the mode by thermal ions for the $q_\mathrm {min}>1.06$![]() cases providing their small growth rates without thermal ions. It is necessary to include the thermal ion kinetic effects and Landau damping in those cases to avoid false positive results.
cases providing their small growth rates without thermal ions. It is necessary to include the thermal ion kinetic effects and Landau damping in those cases to avoid false positive results.
In the above study we scan the value of $q_\mathrm {min}$![]() by varying the toroidal field and keeping the plasma pressure fixed. This can lead to changes in both $q_\mathrm {min}$
by varying the toroidal field and keeping the plasma pressure fixed. This can lead to changes in both $q_\mathrm {min}$![]() and the plasma $\beta$
and the plasma $\beta$![]() at the same time, as discussed in Brennan et al. (Reference Brennan, Kim and Haye2012). To separate the two effects, we rerun the reconstruction of the equilibrium by fixing the toroidal field and $q$
at the same time, as discussed in Brennan et al. (Reference Brennan, Kim and Haye2012). To separate the two effects, we rerun the reconstruction of the equilibrium by fixing the toroidal field and $q$![]() profile while scaling the total pressure, by varying $T_e$
profile while scaling the total pressure, by varying $T_e$![]() , $T_i$
, $T_i$![]() and the fast ion energy. The results of MHD-only simulations and simulations with fast ions and thermal ion kinetic effects are summarized in figure 10, with $q_\mathrm {min}=1.04$
and the fast ion energy. The results of MHD-only simulations and simulations with fast ions and thermal ion kinetic effects are summarized in figure 10, with $q_\mathrm {min}=1.04$![]() . The results indicate that, although the (1,1) mode bears the name ‘non-resonant kink mode’ in some of the literature (Wang et al. Reference Wang, Fu, Breslau and Liu2013), its growth rate has a strong dependence on the plasma beta value, especially for the MHD-only simulations, which is similar to pressure-driven modes. After including ion kinetic effects, the dependence of the growth rate on $\beta$
. The results indicate that, although the (1,1) mode bears the name ‘non-resonant kink mode’ in some of the literature (Wang et al. Reference Wang, Fu, Breslau and Liu2013), its growth rate has a strong dependence on the plasma beta value, especially for the MHD-only simulations, which is similar to pressure-driven modes. After including ion kinetic effects, the dependence of the growth rate on $\beta$![]() weakens, and the mode frequency is almost independent of $\beta$
weakens, and the mode frequency is almost independent of $\beta$![]() .
.

Figure 10. Growth rates (solid lines) and frequencies (dashed lines) of the $n=1$![]() mode with different plasma $\beta$
mode with different plasma $\beta$![]() ($\beta _0$
($\beta _0$![]() is the experimental value) and a fixed $q$
is the experimental value) and a fixed $q$![]() profile. The blue line shows the MHD-only result. The green lines show the kinetic–MHD results with fast and thermal ions.
profile. The blue line shows the MHD-only result. The green lines show the kinetic–MHD results with fast and thermal ions.
With the Landau damping effect included, the $n=1$![]() mode is stable for $q_\mathrm {min}>1.06$
mode is stable for $q_\mathrm {min}>1.06$![]() . For the original equilibrium from EFIT, $q_\mathrm {min}=1.06$
. For the original equilibrium from EFIT, $q_\mathrm {min}=1.06$![]() , the mode is at the stability boundary, which may be the result of nonlinear evolution of the fishbone mode and the flattening of the current profile near the core. The fishbone-like mode in the simulation with $q_\mathrm {min}=1.04$
, the mode is at the stability boundary, which may be the result of nonlinear evolution of the fishbone mode and the flattening of the current profile near the core. The fishbone-like mode in the simulation with $q_\mathrm {min}=1.04$![]() has a frequency of approximately $f=6.13$
has a frequency of approximately $f=6.13$![]() kHz. In the DIII-D experiment, the dominant $n=1$
kHz. In the DIII-D experiment, the dominant $n=1$![]() mode is identified to have a frequency of 18 kHz in the laboratory frame, and the toroidal rotate frequency is approximately 21 kHz. Therefore, the simulation of the fishbone-like mode is consistent with the measured frequency in the plasma frame.
mode is identified to have a frequency of 18 kHz in the laboratory frame, and the toroidal rotate frequency is approximately 21 kHz. Therefore, the simulation of the fishbone-like mode is consistent with the measured frequency in the plasma frame.
5. Linear simulation of fishbone modes in NSTX
We did a similar study for the $n=1$![]() mode under a NSTX experimental condition. The equilibrium $q$
mode under a NSTX experimental condition. The equilibrium $q$![]() profile is obtained from NSTX shot #134020 at 700 ms. The density and temperature profiles are from the TRANSP (Ongena et al. Reference Ongena, Voitsekhovitch, Evrard and McCune2012) calculation result. The Grad-Shafranov (G-S) equation was solved using these profiles in a M3D-C1 two-dimensional mesh with 7199 elements. We ignore the contribution of high-$Z$
profile is obtained from NSTX shot #134020 at 700 ms. The density and temperature profiles are from the TRANSP (Ongena et al. Reference Ongena, Voitsekhovitch, Evrard and McCune2012) calculation result. The Grad-Shafranov (G-S) equation was solved using these profiles in a M3D-C1 two-dimensional mesh with 7199 elements. We ignore the contribution of high-$Z$![]() impurities and assume all the ions are deuterium. The profiles used in the simulation and the shape of the flux contours are shown in figure 11. The $q$
impurities and assume all the ions are deuterium. The profiles used in the simulation and the shape of the flux contours are shown in figure 11. The $q$![]() profile has the same shape as the EFIT $q$
profile has the same shape as the EFIT $q$![]() profile, with $q_\mathrm {min}$
profile, with $q_\mathrm {min}$![]() located at $\sqrt {\psi _{norm}}=0.2$
located at $\sqrt {\psi _{norm}}=0.2$![]() . The core electron density is $1.04\times 10^{20}$
. The core electron density is $1.04\times 10^{20}$![]() m$^{-3}$
m$^{-3}$![]() and the core electron and ion temperature is approximately 0.74 keV. The ratio of EP beta to the total beta at the core is $\beta _\mathrm {EP}/\beta =17.3\,\%$
and the core electron and ion temperature is approximately 0.74 keV. The ratio of EP beta to the total beta at the core is $\beta _\mathrm {EP}/\beta =17.3\,\%$![]() . Note that a key difference from the DIII-D equilibrium is that NSTX has much larger plasma $\beta$
. Note that a key difference from the DIII-D equilibrium is that NSTX has much larger plasma $\beta$![]() ($\beta _\text {on-axis}=50.8\,\%$
($\beta _\text {on-axis}=50.8\,\%$![]() vs. DIII-D $\beta _\text {on-axis}=12.4\,\%$
vs. DIII-D $\beta _\text {on-axis}=12.4\,\%$![]() ). In the NSTX simulation we use the Spitzer resistivity calculated from the local electron temperature, and apply a large value of the parallel heat conduction coefficient $\kappa _\parallel$
). In the NSTX simulation we use the Spitzer resistivity calculated from the local electron temperature, and apply a large value of the parallel heat conduction coefficient $\kappa _\parallel$![]() .
.

Figure 11. (a) Profiles of $q$![]() and pressure of different particle species of the equilibrium used in the NSTX simulation. (b) Flux contours and mesh boundary used in the simulation.
and pressure of different particle species of the equilibrium used in the NSTX simulation. (b) Flux contours and mesh boundary used in the simulation.
For EP we use an anisotropic distribution from the NUBEAM calculation. The NUBEAM code provides three-dimensional ($r$![]() , $\lambda =V_\parallel /V$
, $\lambda =V_\parallel /V$![]() , energy) information of injected beam ions from Monte Carlo calculation (Pankin et al. Reference Pankin, McCune, Andre, Bateman and Kritz2004), which is called the classical fast ion distribution. The NUBEAM distribution near the magnetic axis (figure 12a) shows that the lower-energy EPs ($\mathcal {E}<40$
, energy) information of injected beam ions from Monte Carlo calculation (Pankin et al. Reference Pankin, McCune, Andre, Bateman and Kritz2004), which is called the classical fast ion distribution. The NUBEAM distribution near the magnetic axis (figure 12a) shows that the lower-energy EPs ($\mathcal {E}<40$![]() keV) are mostly co-passing with $V_\parallel /V\approx 1$
keV) are mostly co-passing with $V_\parallel /V\approx 1$![]() , and the higher-energy EPs have a peak distribution at $V_\parallel /V\approx 0.4$
, and the higher-energy EPs have a peak distribution at $V_\parallel /V\approx 0.4$![]() . This initial distribution is quite noisy, making it difficult to calculate the gradients of $f_0$
. This initial distribution is quite noisy, making it difficult to calculate the gradients of $f_0$![]() in the phase space. In order to use it for $\delta f$
in the phase space. In order to use it for $\delta f$![]() calculation, we apply a Gaussian smoothing operator to obtain a smoothed distribution, as shown in figure 12(b). This new distribution is then read into M3D-C1-K as $f_0$
calculation, we apply a Gaussian smoothing operator to obtain a smoothed distribution, as shown in figure 12(b). This new distribution is then read into M3D-C1-K as $f_0$![]() and used for both particle initialization and $\delta f$
and used for both particle initialization and $\delta f$![]() calculation. The radial profile of EP pressure is shown in figure 11, which is consistent with the TRANSP output.
calculation. The radial profile of EP pressure is shown in figure 11, which is consistent with the TRANSP output.

Figure 12. (a) The original EP distribution of energy and pitch angle near the magnetic axis from NUBEAM. (b) The smoothed EP distribution that was used in M3D-C1-K simulations.
In terms of the shortcomings of the Bateman scaling method, and the sensitive dependence of the $n=1$![]() mode growth rate on $\beta$
mode growth rate on $\beta$![]() , as discussed in § 4, for NSTX we apply a new method to scan the value of $q_\mathrm {min}$
, as discussed in § 4, for NSTX we apply a new method to scan the value of $q_\mathrm {min}$![]() , by fixing the toroidal field and changing the plasma current to fit the new $q$
, by fixing the toroidal field and changing the plasma current to fit the new $q$![]() profile. This method ensures that $\beta$
profile. This method ensures that $\beta$![]() is almost fixed when scanning $q_\mathrm {min}$
is almost fixed when scanning $q_\mathrm {min}$![]() . The results of kinetic–MHD and MHD-only $n=1$
. The results of kinetic–MHD and MHD-only $n=1$![]() linear simulations are summarized in figure 13. The threshold value of $q_\mathrm {min}$
linear simulations are summarized in figure 13. The threshold value of $q_\mathrm {min}$![]() for $n=1$
for $n=1$![]() mode excitation is higher than the DIII-D results, thanks to the larger $\beta$
mode excitation is higher than the DIII-D results, thanks to the larger $\beta$![]() . For kinetic–MHD simulations with only fast ions (red lines), the growth rates decrease slightly from the MHD-only results, and the fishbone mode frequencies are almost constant ($\sim$
. For kinetic–MHD simulations with only fast ions (red lines), the growth rates decrease slightly from the MHD-only results, and the fishbone mode frequencies are almost constant ($\sim$![]() 0.4 kHz) as $q_\mathrm {min}$
0.4 kHz) as $q_\mathrm {min}$![]() changes. The AE-like modes do not show up in the NSTX simulations.
changes. The AE-like modes do not show up in the NSTX simulations.

Figure 13. Growth rates $\gamma$![]() (solid lines) and frequencies $f$
(solid lines) and frequencies $f$![]() (dashed lines) as functions of $q_\mathrm {min}$
(dashed lines) as functions of $q_\mathrm {min}$![]() of the $n=1$
of the $n=1$![]() modes from M3D-C1 linear simulation with NSTX equilibrium with fixed $\beta$
modes from M3D-C1 linear simulation with NSTX equilibrium with fixed $\beta$![]() . The blue line shows the MHD-only result. The red lines show the kinetic–MHD results with only fast ions. The green lines show the results with both thermal and energetic ions.
. The blue line shows the MHD-only result. The red lines show the kinetic–MHD results with only fast ions. The green lines show the results with both thermal and energetic ions.
After including the thermal ion kinetic effects, the frequencies of fishbone-like modes increase significantly, while the growth rates decrease because of the precession motion of trapped ions and Landau damping. As shown in figure 12, the population of trapped particles ($\lambda \approx 0$![]() ) in fast ions is relatively small compared with the co-passing ions, which leads to the low frequency of the fishbone-like modes. The thermal ions, on the other hand, have an isotropic distribution and can provide a large population of trapped ions to drive the fishbone-like mode. The mode structure of the fishbone-like mode for $q_\mathrm {min}=1.08$
) in fast ions is relatively small compared with the co-passing ions, which leads to the low frequency of the fishbone-like modes. The thermal ions, on the other hand, have an isotropic distribution and can provide a large population of trapped ions to drive the fishbone-like mode. The mode structure of the fishbone-like mode for $q_\mathrm {min}=1.08$![]() is shown in figure 14. For $q_\mathrm {min}>1.14$
is shown in figure 14. For $q_\mathrm {min}>1.14$![]() , the Landau damping effect stabilizes the AE-like mode, which is similar to the DIII-D results.
, the Landau damping effect stabilizes the AE-like mode, which is similar to the DIII-D results.

Figure 14. Two-dimensional structure of $\delta \phi$![]() (a) and $\delta \psi$
(a) and $\delta \psi$![]() (b) from NSTX $n=1$
(b) from NSTX $n=1$![]() linear simulation of the $q_\mathrm {min}=1.08$
linear simulation of the $q_\mathrm {min}=1.08$![]() case with thermal ions.
case with thermal ions.
In the NSTX experiment, both the kink ($m=1$![]() ) and tearing ($m=2$
) and tearing ($m=2$![]() ) modes have been identified using soft X-ray diagnostics, and the synergy effect of the two modes can lead to fast ion transport (Yang, Podestà & Fredrickson Reference Yang, Podestà and Fredrickson2021). It is believed that the $m=2$
) modes have been identified using soft X-ray diagnostics, and the synergy effect of the two modes can lead to fast ion transport (Yang, Podestà & Fredrickson Reference Yang, Podestà and Fredrickson2021). It is believed that the $m=2$![]() mode is mainly a neoclassical tearing mode which is affected by the current associated with EPs. The $m=1$
mode is mainly a neoclassical tearing mode which is affected by the current associated with EPs. The $m=1$![]() mode is marginally unstable in the M3D-C1-K simulation with thermal ions under experimental conditions ($1.1< q_\mathrm {min}<1.2$
mode is marginally unstable in the M3D-C1-K simulation with thermal ions under experimental conditions ($1.1< q_\mathrm {min}<1.2$![]() ), similar to the DIII-D case, which may be a result of pressure and current relaxation due to the nonlinear saturation of the fishbone mode. The frequency observed in the experiment is less than 5 kHz after subtracting the Doppler frequency of toroidal rotation, which is close to the simulation frequency with $q_\mathrm {min}=1.1$
), similar to the DIII-D case, which may be a result of pressure and current relaxation due to the nonlinear saturation of the fishbone mode. The frequency observed in the experiment is less than 5 kHz after subtracting the Doppler frequency of toroidal rotation, which is close to the simulation frequency with $q_\mathrm {min}=1.1$![]() . Note that the oscillation frequency after nonlinear saturation can be lower than the linear result due to the downchirping of the fishbone mode.
. Note that the oscillation frequency after nonlinear saturation can be lower than the linear result due to the downchirping of the fishbone mode.
6. Nonlinear simulation of the fishbone-like mode in NSTX
Based on the linear simulation, we conduct a nonlinear simulation of the $n=1$![]() fishbone-like mode including the thermal ion kinetic effects in NSTX. We use the same MHD equilibrium and EP distribution as in § 5, with $q_\mathrm {min}=1.08$
fishbone-like mode including the thermal ion kinetic effects in NSTX. We use the same MHD equilibrium and EP distribution as in § 5, with $q_\mathrm {min}=1.08$![]() . The simulation utilized a three-dimensional finite element mesh, and nonlinear terms are included in the MHD and $\delta f$
. The simulation utilized a three-dimensional finite element mesh, and nonlinear terms are included in the MHD and $\delta f$![]() equations. The mesh has 8 toroidal planes connected by Hermite finite elements in the toroidal direction, which is good enough to resolve the $n=1$
equations. The mesh has 8 toroidal planes connected by Hermite finite elements in the toroidal direction, which is good enough to resolve the $n=1$![]() perturbation, as we focus on the growth and saturation of the $n=1$
perturbation, as we focus on the growth and saturation of the $n=1$![]() mode and its nonlinear coupling with the $n=0$
mode and its nonlinear coupling with the $n=0$![]() mode in this simulation. The mesh structure of each plane is the same as in the linear simulation. We use $16\times 10^6$
mode in this simulation. The mesh structure of each plane is the same as in the linear simulation. We use $16\times 10^6$![]() particle markers for the PIC simulation.
particle markers for the PIC simulation.
The nonlinear simulation was conducted at the Perlmutter cluster at NERSC. For each nonlinear simulation we use 8 nodes with 64 AMD cores and 4 NVIDIA Tesla A100 GPUs on each node. The GPUs are used to do the MHD equation matrix element calculation and particle pushing. The CPU was used to solve the matrix by calling PETSC library, and calculate the particle moments.
The time evolution of the kinetic and magnetic parts of the MHD energy in the nonlinear NSTX fishbone simulation is shown in figure 15. We find that the $n=1$![]() mode reaches a saturation point at approximately $t=0.5$
mode reaches a saturation point at approximately $t=0.5$![]() ms. The peak $\delta B/B_0$
ms. The peak $\delta B/B_0$![]() at this point is approximately $2.0\times 10^{-2}$
at this point is approximately $2.0\times 10^{-2}$![]() , and the perturbed electron temperature has a maximum of approximately 86 eV (10 % of the equilibrium on-axis $T_e$
, and the perturbed electron temperature has a maximum of approximately 86 eV (10 % of the equilibrium on-axis $T_e$![]() ). There is also an $n=0$
). There is also an $n=0$![]() mode excited due to the nonlinear mode–mode coupling. After saturation, the magnetic energy of the $n=1$
mode excited due to the nonlinear mode–mode coupling. After saturation, the magnetic energy of the $n=1$![]() mode has some oscillations at a high level, and the energy of the $n=0$
mode has some oscillations at a high level, and the energy of the $n=0$![]() mode keeps growing, meaning that the change to the magnetic field topology does not decay. The Poincaré plot of the magnetic flux after mode saturation ($t=1.2$
mode keeps growing, meaning that the change to the magnetic field topology does not decay. The Poincaré plot of the magnetic flux after mode saturation ($t=1.2$![]() ms) is shown in figure 16(a). There is a clear shift of the magnetic axis due to the excitation of (1,1) mode. The kink boundary overlaps with the flux contour of $q=q_\mathrm {min}$
ms) is shown in figure 16(a). There is a clear shift of the magnetic axis due to the excitation of (1,1) mode. The kink boundary overlaps with the flux contour of $q=q_\mathrm {min}$![]() , meaning that most of the magnetic perturbation happens in the reversed shear region. Although the equilibrium has $q_0>1.08$
, meaning that most of the magnetic perturbation happens in the reversed shear region. Although the equilibrium has $q_0>1.08$![]() , the excited mode creates a (1,1) island near the magnetic axis, and makes the magnetic fields near the $q=q_\mathrm {min}$
, the excited mode creates a (1,1) island near the magnetic axis, and makes the magnetic fields near the $q=q_\mathrm {min}$![]() flux surface stochastic. It also creates small (2,1) islands near the $q=2$
flux surface stochastic. It also creates small (2,1) islands near the $q=2$![]() surface.
surface.

Figure 15. Time evolution of kinetic energy (a) and magnetic energy (b) of different toroidal harmonics from NSTX nonlinear simulation of the $q_\mathrm {min}=1.08$![]() case with thermal ions.
case with thermal ions.

Figure 16. (a) Poincaré plot of magnetic flux surfaces at $t=1.2$![]() ms. The (1,1) and (2,1) islands are marked as red. (b) Change of fast ion density profile in the nonlinear simulation of $q_\mathrm {min}=1.08$
ms. The (1,1) and (2,1) islands are marked as red. (b) Change of fast ion density profile in the nonlinear simulation of $q_\mathrm {min}=1.08$![]() due to mode excitation.
due to mode excitation.
The growth of the $n=1$![]() mode can lead to transport of EPs. Figure 16(b) shows the flux-averaged profiles of EP density before and after mode saturation. This result shows that, although the $n=1$
mode can lead to transport of EPs. Figure 16(b) shows the flux-averaged profiles of EP density before and after mode saturation. This result shows that, although the $n=1$![]() mode can provide a large $\delta B$
mode can provide a large $\delta B$![]() field, it only leads to a slight drop of EP density (approximately 10 %) near the radial location at $q=q_\mathrm {min}$
field, it only leads to a slight drop of EP density (approximately 10 %) near the radial location at $q=q_\mathrm {min}$![]() ($\rho =0.2$
($\rho =0.2$![]() ). The profile gradient does not drop to zero after saturation because the mode is susceptible to Landau damping, which means that is requires a finite radial gradient to excite. However, figure 16(b) is a flux-averaged result and does not show the change of gradient along the mode's resonance line in phase space, which may be more significant.
). The profile gradient does not drop to zero after saturation because the mode is susceptible to Landau damping, which means that is requires a finite radial gradient to excite. However, figure 16(b) is a flux-averaged result and does not show the change of gradient along the mode's resonance line in phase space, which may be more significant.
Note that the nonlinear saturation results depend sensitively on the value of $q_\mathrm {min}$![]() just like the linear growth rates. We have also done the nonlinear simulation for NSTX with $q_\mathrm {min}=1.1$
just like the linear growth rates. We have also done the nonlinear simulation for NSTX with $q_\mathrm {min}=1.1$![]() , using the same plasma and EP $\beta$
, using the same plasma and EP $\beta$![]() . We find that, in this case, the mode can saturate at a much lower level. The saturation value of $\delta B/B_0$
. We find that, in this case, the mode can saturate at a much lower level. The saturation value of $\delta B/B_0$![]() is approximately $3.3\times 10^{-3}$
is approximately $3.3\times 10^{-3}$![]() , and the maximum $\delta T\_e$
, and the maximum $\delta T\_e$![]() is approximately 20 eV. The perturbed fields are too small to create magnetic islands or drive noticeable transport of EPs. Given that this small change of $q_\mathrm {min}$
is approximately 20 eV. The perturbed fields are too small to create magnetic islands or drive noticeable transport of EPs. Given that this small change of $q_\mathrm {min}$![]() can be within the error bar of the $q$
can be within the error bar of the $q$![]() measurement in experiments, it is difficult to give a definite answer on the nonlinear behaviour of the fishbone mode using current diagnostics through numerical simulation.
measurement in experiments, it is difficult to give a definite answer on the nonlinear behaviour of the fishbone mode using current diagnostics through numerical simulation.
7. Summary
The new kinetic–MHD simulation approach in this paper includes all the ions as kinetic particles, which is different from the classical approach that only deals with kinetic effects of fast ions. To implement this, part of the MHD equations, the density equation and the parallel velocity equation, are replaced by synchronization from kinetic particle simulation, to avoid redundant calculation and parasitic modes caused by numerical errors. The rest of the MHD equations can still be solved using a semi-implicit method with a large timestep, which is different from the fully kinetic or gyrokinetic simulation approach. The inclusion of thermal ion kinetic effects is important for macroscopic instability simulations targeting ITER and fusion reactors with a large ion temperature.
The new simulation method has been used to study the thermal ion Landau damping of IAWs and fishbone modes. It is found that the $n=1$![]() fishbone modes driven in an equilibrium with $q_\mathrm {min}>1$
fishbone modes driven in an equilibrium with $q_\mathrm {min}>1$![]() , or non-resonant fishbone modes, can be strongly affected by the Landau damping effects, since the mode phase velocity in the parallel direction is of the same order as the ion thermal velocity. In the linear simulation using a DIII-D and NSTX equilibrium, it is found that the $n=1$
, or non-resonant fishbone modes, can be strongly affected by the Landau damping effects, since the mode phase velocity in the parallel direction is of the same order as the ion thermal velocity. In the linear simulation using a DIII-D and NSTX equilibrium, it is found that the $n=1$![]() AE-like modes driven by fast ions can be stabilized by the thermal ions. Therefore it is necessary to revisit those non-resonant fishbone simulations done by kinetic–MHD codes, and add the thermal ion kinetic effects. Further analysis of the AE-like modes in the large $q_\mathrm {min}$
AE-like modes driven by fast ions can be stabilized by the thermal ions. Therefore it is necessary to revisit those non-resonant fishbone simulations done by kinetic–MHD codes, and add the thermal ion kinetic effects. Further analysis of the AE-like modes in the large $q_\mathrm {min}$![]() cases can be done using an eigenvalue code like NOVA, which will be conducted in the future.
cases can be done using an eigenvalue code like NOVA, which will be conducted in the future.
In developing the kinetic–MHD method, we include the parallel electric field calculated from the electron pressure in the kinetic equations, which is essential for the IAW simulation. This term, however, is not included in Ohm's law in the MHD equations. The two-fluid terms, including the parallel and perpendicular electric fields driven by Hall terms and electron pressure, can be important for the calculation of plasma waves with wavelengths comparable to the ion skin depth, such as KAWs and whistler waves. The two-fluid terms have been developed in M3D-C1 and used to calculate their effects on magnetic reconnection (Beidler et al. Reference Beidler, Cassak, Jardin and Ferraro2016), but simulation with them requires further testing and improvement of the matrix solver. We plan to do simulations with electric fields in both fluid and kinetic equations, to study the two-fluid effects self-consistently in future work.
Acknowledgements
We would like to thank Y. Todo, M. Sato, R. Ma, F. Wang, X. Zhu, Z. Lin, G. Brochard, G. Dong and C. Kim for fruitful discussion. This work was supported by US Department of Energy grants DE-AC02-09CH11466. This research used the Traverse cluster at Princeton University. This research also used the Perlmutter cluster of the National Energy Research Scientific Computing Center (NERSC), using a NERSC NESAP Tier 2 award.
Editor William Dorland thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.