Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T21:47:43.620Z Has data issue: false hasContentIssue false
  • English
  • Français

Transverse instability of electron phase-space holes in multi-dimensional Maxwellian plasmas

Published online by Cambridge University Press:  05 November 2018

I. H. Hutchinson Open the ORCID record for I. H. Hutchinson [Opens in a new window]
I. H. Hutchinson*
Affiliation:
Plasma Science and Fusion Center, MIT, Cambridge, MA 02139, USA
*
†Email address for correspondence: ihutch@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The stability of an initially one-dimensional electron hole to perturbations varying sinusoidally transverse to its trapping direction is analysed in detail. It is shown that the expected low-frequency eigenmode of the linearized Vlasov–Poisson system consists of a shift mode, proportional to the gradient of the equilibrium potential. The resulting dispersion relation is that the total jetting force exerted by a perturbed hole on the particles balances the electric restoring tension of the hole. The tension is quantitatively small and can often be ignored. The particle force is expressed as integrals of equilibrium parameters over the hole and is shown at low frequency to be exactly equal to what has recently been found (by different analysis) to express ‘kinematic’ hole momentum conservation. The mechanism of instability has nothing to do with the previously hypothesized transverse electron focusing. The unmagnetized growth rate 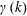$\unicode[STIX]{x1D6FE}(k)$ is found numerically and is in excellent agreement with recent kinematic estimates. Magnetic field stabilization of the transverse mode is also evaluated. The resulting stability boundary for Maxwellian holes is in reasonable agreement with previously published criteria based on particle simulation. It arises from a change of trapped force sign across the resonance between bounce and cyclotron frequencies.

Keywords

plasma instabilitiesplasma nonlinear phenomenaspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 4 , August 2018 , 905840411
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, L., Ergun, R. E., Tao, J., Roux, A., Lecontel, O., Angelopoulos, V., Bonnell, J., McFadden, J. P., Larson, D. E., Eriksson, S. et al. 2009 New features of electron phase space holes observed by the THEMIS mission. Phys. Rev. Lett. 102 (22), 225004.Google Scholar
Bale, S. D., Kellogg, P. J., Larsen, D. E., Lin, R. P., Goetz, K. & Lepping, R. P. 1998 Bipolar electrostatic structures in the shock transition region: evidence of electron phase space holes. Geophys. Res. Lett. 25 (15), 2929–2932.Google Scholar
Bernstein, I. B., Greene, J. M. & Kruskal, M. D. 1957 Exact nonlinear plasma oscillations. Phys. Rev. 108 (4), 546–550.Google Scholar
Berthomier, M., Muschietti, L., Bonnell, J. W., Roth, I. & Carlson, C. W. 2002 Interaction between electrostatic whistlers and electron holes in the auroral region. J. Geophys. Res. 107 (A12), 1–11.Google Scholar
Eliasson, B. & Shukla, P. K. 2006 Formation and dynamics of coherent structures involving phase-space vortices in plasmas. Phys. Rep. 422 (6), 225–290.Google Scholar
Ergun, R. E., Carlson, C. W., McFadden, J. P., Mozer, F. S., Muschietti, L., Roth, I. & Strangeway, R. J. 1998 Debye-scale plasma structures associated with magnetic-field-aligned electric fields. Phys. Rev. Lett. 81 (4), 826–829.Google Scholar
Goldman, M. V., Oppenheim, M. M. & Newman, D. L. 1999 Nonlinear two-stream instabilities as an explanation for auroral bipolar wave structures. Geophys. Res. Lett. 26 (13), 1821–1824.Google Scholar
Hutchinson, I. H. 2017 Electron holes in phase space: What they are and why they matter. Phys. Plasmas 24 (5), 055601.Google Scholar
Hutchinson, I. H. 2018 On the mechanism of plasma electron hole transverse instability. Phys. Rev. Lett. 120 (20), 205101.Google Scholar
Hutchinson, I. H. & Zhou, C. 2016 Plasma electron hole kinematics. I. Momentum conservation. Phys. Plasmas 23 (8), 82101.Google Scholar
Jovanović, D. & Schamel, H. 2002 The stability of propagating slab electron holes in a magnetized plasma. Phys. Plasmas 9 (12), 5079–5087.Google Scholar
Lewis, H. R. & Seyler, C. 1982 Stability of Vlasov Equilibria. Part 2. One ignorable coordinate. J. Plasma Phys. 27, 25–35.Google Scholar
Lewis, H. R. & Symon, K. R. 1979 Linearized analysis of inhomogeneous plasma equilibria: general theory. J. Math. Phys. 20 (1979), 413.Google Scholar
Lu, Q. M., Lembege, B., Tao, J. B. & Wang, S. 2008 Perpendicular electric field in two-dimensional electron phase-holes: a parameter study. J. Geophys. Res. 113 (A11), A11219.Google Scholar
Malaspina, D. M., Andersson, L., Ergun, R. E., Wygant, J. R., Bonnell, J. W., Kletzing, C., Reeves, G. D., Skoug, R. M. & Larsen, B. A. 2014 Nonlinear electric field structures in the inner magnetosphere. Geophys. Res. Lett. 41, 5693–5701.Google Scholar
Malaspina, D. M., Newman, D. L., Willson, L. B., Goetz, K., Kellogg, P. J. & Kerstin, K. 2013 Electrostatic solitary waves in the solar wind: evidence for instability at solar wind current sheets. J. Geophys. Res. 118 (2), 591–599.Google Scholar
Mangeney, A., Salem, C., Lacombe, C., Bougeret, J.-L., Perche, C., Manning, R., Kellogg, P. J., Goetz, K., Monson, S. J. & Bosqued, J.-M. 1999 WIND observations of coherent electrostatic waves in the solar wind. Ann. Geophys. 17 (3), 307–320.Google Scholar
Matsumoto, H., Kojima, H., Miyatake, T., Omura, Y., Okada, M., Nagano, I. & Tsutsui, M. 1994 Electrostatic solitary waves (ESW) in the magnetotail: BEN wave forms observed by GEOTAIL. Geophys. Res. Lett. 21 (25), 2915–2918.Google Scholar
Miyake, T., Omura, Y., Matsumoto, H. & Kojima, H. 1998 Two-dimensional computer simulations of electrostatic solitary waves observed by Geotail spacecraft. J. Geophys. Res. 103 (A6), 11841.Google Scholar
Morse, R. L. & Nielson, C. W. 1969 One-, two-, and three-dimensional numerical simulation of two-beam plasmas. Phys. Rev. Lett. 23 (19), 1087–1090.Google Scholar
Mottez, F., Perraut, S., Roux, A. & Louarn, P. 1997 Coherent structures in the magnetotail triggered by counterstreaming electron beams. J. Geophys. Res. 102 (A6), 11399.Google Scholar
Mozer, F. S., Agapitov, O. A., Artemyev, A., Burch, J. L., Ergun, R. E., Giles, B. L., Mourenas, D., Torbert, R. B., Phan, T. D. & Vasko, I. 2016 Magnetospheric multiscale satellite observations of parallel electron acceleration in magnetic field reconnection by Fermi reflection from time domain structures. Phys. Rev. Lett. 116 (14), 4–8.Google Scholar
Muschietti, L., Roth, I., Carlson, C. W. & Ergun, R. E. 2000 Transverse instability of magnetized electron holes. Phys. Rev. Lett. 85 (1), 94–97.Google Scholar
Muschietti, L., Roth, I., Ergun, R. E. & Carlson, C. W. 1999 Analysis and simulation of BGK electron holes. Nonlinear Process. Geophys. 6 (3/4), 211–219.Google Scholar
Newman, D. L., Goldman, M. V., Spector, M. & Perez, F. 2001 Dynamics and instability of electron phase-space tubes. Phys. Rev. Lett. 86 (7), 1239–1242.Google Scholar
Oppenheim, M., Newman, D. L. & Goldman, M. V. 1999 Evolution of electron phase-space holes in a 2D magnetized plasma. Phys. Rev. Lett. 83 (12), 2344–2347.Google Scholar
Oppenheim, M. M., Vetoulis, G., Newman, D. L. & Goldman, M. V. 2001 Evolution of electron phase-space holes in 3D. Geophys. Res. Lett. 28 (9), 1891–1894.Google Scholar
Pickett, J. S., Chen, L.-J., Mutel, R. L., Christopher, I. W., Santolk, O., Lakhina, G. S., Singh, S. V., Reddy, R. V., Gurnett, D. A., Tsurutani, B. T. et al. 2008 Furthering our understanding of electrostatic solitary waves through Cluster multispacecraft observations and theory. Adv. Space Res. 41 (10), 1666–1676.Google Scholar
Schamel, H. 1979 Theory of electron holes. Phys. Scr. 20 (3–4), 336–342.Google Scholar
Schamel, H. 1982 Stability of electron vortex structures in phase space. Phys. Rev. Lett. 48 (7), 481–483.Google Scholar
Schamel, H. 1986 Electrostatic phase space structures in theory and experiment. Phys. Rep. 3 (3), 161–191.Google Scholar
Schamel, H. 1987 On the stability of localized electrostatic structures. Z. Naturforsch. 42a, 1167–1174.Google Scholar
Singh, N., Loo, S. M. & Wells, B. E. 2001 Electron hole structure and its stability depending on plasma magnetization. J. Geophys. Res. 106 (A10), 21183–21198.Google Scholar
Skryabin, D. V. 2002 Energy of the soliton internal modes and broken symmetries in nonlinear optics. J. Opt. Soc. Am. B 19 (3), 529–536.Google Scholar
Turikov, V. A. 1984 Electron phase space holes as localized BGK solutions. Phys. Scr. 30 (1), 73–77.Google Scholar
Vasko, I. Y., Agapitov, O. V., Mozer, F., Artemyev, A. V. & Jovanovic, D. 2015 Magnetic field depression within electron holes. Geophys. Res. Lett. 42 (7), 2123–2129.Google Scholar
Vetoulis, G. & Oppenheim, M. 2001 Electrostatic mode excitation in electron holes due to wave bounce resonances. Phys. Rev. Lett. 86 (7), 1235–1238.Google Scholar
Wilson, L. B., Cattell, C. A., Kellogg, P. J., Goetz, K., Kersten, K., Kasper, J. C., Szabo, A. & Wilber, M. 2010 Large-amplitude electrostatic waves observed at a supercritical interplanetary shock. J. Geophys. Res. 115 (12), A12104.Google Scholar
Wu, M., Lu, Q., Huang, C. & Wang, S. 2010 Transverse instability and perpendicular electric field in two-dimensional electron phase-space holes. J. Geophys. Res. 115 (10), A10245.Google Scholar
Zhou, C. & Hutchinson, I. H. 2016 Plasma electron hole kinematics. II. Hole tracking particle-in-cell simulation. Phys. Plasmas 23 (8), 82102.Google Scholar
Zhou, C. & Hutchinson, I. H. 2017 Plasma electron hole ion-acoustic instability. J. Plasma Phys. 83, 90580501.Google Scholar