1. Introduction
In magnetic confinement fusion devices, there are usually three processes limiting the energy confinement: radiation losses, neoclassical transport, which encompasses collisional diffusion – including the effect of particle drifts that arise due to gradients and curvature of the confining magnetic field – and turbulence. While tokamaks are never critically affected by collisional transport owing to their axisymmetry, stellarators historically suffered from poor confinement due to the lack of symmetry and the resulting high neoclassical transport losses at high temperature. Optimised stellarators using the concepts of quasi-symmetry (Nührenberg & Zille Reference Nührenberg and Zille1988; Boozer Reference Boozer1995), like the quasi-helically symmetric experiment HSX (Anderson et al. Reference Anderson, Almagri, Anderson, Matthews, Talmadge and Shohet1995), or quasi-isodynamicity (Helander & Nührenberg Reference Helander and Nührenberg2009; Nührenberg Reference Nührenberg2010), like the recent superconducting stellarator Wendelstein 7-X (W7-X) (Beidler et al. Reference Beidler, Grieger, Hernegger, Harmeyer, Kisslinger, Lotz, Maaberg, Merkel, Nührenberg and Rau1990; Klinger et al. Reference Klinger, Baylard, Beidler, Boscary, Bosch, Dinklage, Hartmann, Helander, Maberg and Peacock2013), are designed to overcome the problem of large neoclassical transport (Canik et al. Reference Canik, Anderson, Anderson, Likin, Talmadge and Zhai2007; Beidler et al. Reference Beidler, Allmaier, Isaev, Kasilov, Kernbichler, Leitold, Maaberg, Mikkelsen, Murakami and Schmidt2011), rendering turbulence the dominant transport channel. As in tokamaks, ion-temperature-gradient (ITG) modes and trapped-electron modes (TEMs) have been identified as the most transport-relevant amongst the electrostatic instabilities. Recent research has focussed on studying the effects of the magnetic geometry available to stellarators on the instability of the ITG mode and TEM. For quasi-isodynamic and other omnigeneous stellarators, the second adiabatic invariant ${\rm J}$![]() of fast-bouncing particles such as electrons is constant on flux surfaces with flux surface label $\psi$
of fast-bouncing particles such as electrons is constant on flux surfaces with flux surface label $\psi$![]() (Helander Reference Helander2014) and depends through the velocity $v$
(Helander Reference Helander2014) and depends through the velocity $v$![]() on the total energy $E$
on the total energy $E$![]() with $\partial {\rm J} / \partial E >0$
with $\partial {\rm J} / \partial E >0$![]() at high normalised plasma pressure:
at high normalised plasma pressure:
where $v_{\|}$![]() denotes the velocity parallel to the magnetic field. If now an instability with frequency below the bounce frequency, $\omega \tau _b \ll 1$
denotes the velocity parallel to the magnetic field. If now an instability with frequency below the bounce frequency, $\omega \tau _b \ll 1$![]() , moves a particle outwards by $\Delta \psi$
, moves a particle outwards by $\Delta \psi$![]() , the energy $\Delta E$
, the energy $\Delta E$![]() necessary for this follows from the conservation of ${\rm J}$
necessary for this follows from the conservation of ${\rm J}$![]() (Helander et al. Reference Helander, Beidler, Bird, Drevlak, Feng, Hatzky, Jenko, Kleiber, Proll and Turkin2012):
(Helander et al. Reference Helander, Beidler, Bird, Drevlak, Feng, Hatzky, Jenko, Kleiber, Proll and Turkin2012):
This means the movement is at the expense of the instability and thus is stabilising if $\partial {\rm J} / \partial \psi <0$![]() , i.e. if ${\rm J}$
, i.e. if ${\rm J}$![]() has its maximum at the magnetic axis (Rosenbluth Reference Rosenbluth1968). Proll et al. (Reference Proll, Helander, Connor and Plunk2012) and Helander, Proll & Plunk (Reference Helander, Proll and Plunk2013) showed analytically that stellarators with the maximum-${\rm J}$
has its maximum at the magnetic axis (Rosenbluth Reference Rosenbluth1968). Proll et al. (Reference Proll, Helander, Connor and Plunk2012) and Helander, Proll & Plunk (Reference Helander, Proll and Plunk2013) showed analytically that stellarators with the maximum-${\rm J}$![]() property, where all trapped electrons can be shown to experience bounce-averaged ‘good’ curvature, $\omega _{*e}\bar {\omega }_{de}<0$
property, where all trapped electrons can be shown to experience bounce-averaged ‘good’ curvature, $\omega _{*e}\bar {\omega }_{de}<0$![]() (where $\omega _{*e}$
(where $\omega _{*e}$![]() is the electron drift wave frequency and $\bar {\omega }_{de}$
is the electron drift wave frequency and $\bar {\omega }_{de}$![]() is the bounce-averaged magnetic drift frequency of the electrons), should be largely stable to collisionless electron-driven TEM thanks to the stabilising property of the trapped electrons. While the theory states that this resilience should hold for perfectly quasi-isodynamic stellarators with the maximum-${\rm J}$
is the bounce-averaged magnetic drift frequency of the electrons), should be largely stable to collisionless electron-driven TEM thanks to the stabilising property of the trapped electrons. While the theory states that this resilience should hold for perfectly quasi-isodynamic stellarators with the maximum-${\rm J}$![]() property, linear simulations (Proll, Xanthopoulos & Helander Reference Proll, Xanthopoulos and Helander2013; Alcusón et al. Reference Alcusón, Xanthopoulos, Plunk, Helander, Wilms, Turkin, Stechow and Grulke2020) showed that W7-X, which is only approximately quasi-isodynamic, indeed benefits from reduced TEM growth rates, too. These results are however only linear and raise the question whether the enhanced stability actually results in less turbulent transport. Recent nonlinear analytical theory using the concept of available energy (Helander Reference Helander2017, Reference Helander2020) and preliminary simulations (Helander et al. Reference Helander, Bird, Jenko, Kleiber, Plunk, Proll, Riemann and Xanthopoulos2015; Xanthopoulos et al. Reference Xanthopoulos, Bozhenkov, Beurskens, Smith, Plunk, Helander, Beidler, Alcusón, Alonso and Dinklage2020) have hinted that this is indeed the case. The present paper investigates the question directly, demonstrating the fully nonlinear effect of trapped electron stabilisation on TEM turbulence, and also how the effect extends to ITG turbulence, by comparing simulation results obtained in the high-mirror configuration of W7-X, HSX and the DIII-D tokamak (Luxon Reference Luxon2002). We also provide analytical arguments for why, in quasi-isodynamic configurations, trapped electrons also have a stabilising property for ITG modes.
property, linear simulations (Proll, Xanthopoulos & Helander Reference Proll, Xanthopoulos and Helander2013; Alcusón et al. Reference Alcusón, Xanthopoulos, Plunk, Helander, Wilms, Turkin, Stechow and Grulke2020) showed that W7-X, which is only approximately quasi-isodynamic, indeed benefits from reduced TEM growth rates, too. These results are however only linear and raise the question whether the enhanced stability actually results in less turbulent transport. Recent nonlinear analytical theory using the concept of available energy (Helander Reference Helander2017, Reference Helander2020) and preliminary simulations (Helander et al. Reference Helander, Bird, Jenko, Kleiber, Plunk, Proll, Riemann and Xanthopoulos2015; Xanthopoulos et al. Reference Xanthopoulos, Bozhenkov, Beurskens, Smith, Plunk, Helander, Beidler, Alcusón, Alonso and Dinklage2020) have hinted that this is indeed the case. The present paper investigates the question directly, demonstrating the fully nonlinear effect of trapped electron stabilisation on TEM turbulence, and also how the effect extends to ITG turbulence, by comparing simulation results obtained in the high-mirror configuration of W7-X, HSX and the DIII-D tokamak (Luxon Reference Luxon2002). We also provide analytical arguments for why, in quasi-isodynamic configurations, trapped electrons also have a stabilising property for ITG modes.
2. ITG-stabilisation through trapped electrons
To argue why trapped electrons in maximum-${\rm J}$![]() configurations are also stabilising for ITG modes, we investigate the ITG in two different limits: near marginal stability and in the strongly driven limit. Near marginal stability, we can revisit the derivation from Proll et al. (Reference Proll, Helander, Connor and Plunk2012) and Helander et al. (Reference Helander, Proll and Plunk2013), where we defined the rate of gyrokinetic energy transfer from the electrostatic field to species $a$
configurations are also stabilising for ITG modes, we investigate the ITG in two different limits: near marginal stability and in the strongly driven limit. Near marginal stability, we can revisit the derivation from Proll et al. (Reference Proll, Helander, Connor and Plunk2012) and Helander et al. (Reference Helander, Proll and Plunk2013), where we defined the rate of gyrokinetic energy transfer from the electrostatic field to species $a$![]() as
as
Here, $e_a$![]() is the charge of particle species $a$
is the charge of particle species $a$![]() , $\phi ^\ast$
, $\phi ^\ast$![]() is the complex conjugate of the electrostatic potential, ${\rm J}_0$
is the complex conjugate of the electrostatic potential, ${\rm J}_0$![]() is the zeroth-order Bessel function of the first kind, $v_{\bot }$
is the zeroth-order Bessel function of the first kind, $v_{\bot }$![]() is the velocity perpendicular to the magnetic field, $\varOmega _a$
is the velocity perpendicular to the magnetic field, $\varOmega _a$![]() is the Larmor frequency of species $a$
is the Larmor frequency of species $a$![]() and $k_{\bot }$
and $k_{\bot }$![]() is the magnitude of the perpendicular wave vector $\boldsymbol {k}_{\bot }=k_{\psi } \boldsymbol {\nabla } \psi + k_{\alpha }\boldsymbol {\nabla } \alpha$
is the magnitude of the perpendicular wave vector $\boldsymbol {k}_{\bot }=k_{\psi } \boldsymbol {\nabla } \psi + k_{\alpha }\boldsymbol {\nabla } \alpha$![]() with $\alpha$
with $\alpha$![]() being the binormal coordinate used in the Clebsch representation of the magnetic field, $\boldsymbol {B}=\boldsymbol {\nabla }\psi \times \boldsymbol {\nabla } \alpha$
being the binormal coordinate used in the Clebsch representation of the magnetic field, $\boldsymbol {B}=\boldsymbol {\nabla }\psi \times \boldsymbol {\nabla } \alpha$![]() . The magnetic drift frequency is given by $\omega _{da}=\boldsymbol {k}_{\bot }\boldsymbol {\cdot } \boldsymbol {v}_{d a}$
. The magnetic drift frequency is given by $\omega _{da}=\boldsymbol {k}_{\bot }\boldsymbol {\cdot } \boldsymbol {v}_{d a}$![]() , with the drift velocity $\boldsymbol {v}_{d a}={\hat {\boldsymbol {b}}}/{\varOmega _{a}} \times (({v_{\perp }^{2}}/{2}) \boldsymbol {\nabla } \ln B+v_{\|}^{2} \hat {\boldsymbol {b}}\boldsymbol {\cdot }\boldsymbol {\nabla } \hat {\boldsymbol {b}})$
, with the drift velocity $\boldsymbol {v}_{d a}={\hat {\boldsymbol {b}}}/{\varOmega _{a}} \times (({v_{\perp }^{2}}/{2}) \boldsymbol {\nabla } \ln B+v_{\|}^{2} \hat {\boldsymbol {b}}\boldsymbol {\cdot }\boldsymbol {\nabla } \hat {\boldsymbol {b}})$![]() , where $\hat {\boldsymbol {b}}$
, where $\hat {\boldsymbol {b}}$![]() is the unit vector along the magnetic field. Additionally, $g_a=f_{a1}+({e_a\phi }/{T_a})f_{a0}$
is the unit vector along the magnetic field. Additionally, $g_a=f_{a1}+({e_a\phi }/{T_a})f_{a0}$![]() denotes the non-adiabatic part of the perturbed distribution function with the equilibrium distribution function $f_{a0}$
denotes the non-adiabatic part of the perturbed distribution function with the equilibrium distribution function $f_{a0}$![]() being Maxwellian and $T_a$
being Maxwellian and $T_a$![]() the temperature of species $a$
the temperature of species $a$![]() . We have also used the notation
. We have also used the notation
i.e. we integrate over velocity space and along the field line in Ballooning space (Connor, Hastie & Taylor Reference Connor, Hastie and Taylor1979). It was shown that when using the general solutions of the linear electrostatic gyrokinetic equations as introduced by Connor, Hastie & Taylor (Reference Connor, Hastie and Taylor1980) and Tang, Connor & Hastie (Reference Tang, Connor and Hastie1980), thus imposing no limit on the frequency $\omega$![]() of the instability, the energy transfer rate near marginal stability can be written as
of the instability, the energy transfer rate near marginal stability can be written as
where $\mathrm {Pos}_a(x,\omega )$![]() is a positive definite function and the velocity-dependent diamagnetic frequency is given by $\omega _{*a}^T = \omega _{*a} [1 + \eta _a (x^2 - 3/2)]$
is a positive definite function and the velocity-dependent diamagnetic frequency is given by $\omega _{*a}^T = \omega _{*a} [1 + \eta _a (x^2 - 3/2)]$![]() , with $\omega _{*a} = (T_a k_{\alpha }/e_a) \,{\rm d} \ln n_a / {\rm d} \psi$
, with $\omega _{*a} = (T_a k_{\alpha }/e_a) \,{\rm d} \ln n_a / {\rm d} \psi$![]() , $x^2 = m_a v^2 / 2 T_a$
, $x^2 = m_a v^2 / 2 T_a$![]() and $\eta _a = {\rm d} \ln T_a / {\rm d} \ln n_a$
and $\eta _a = {\rm d} \ln T_a / {\rm d} \ln n_a$![]() as the ratio between the temperature and density gradients (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander et al. Reference Helander, Proll and Plunk2013). For a typical ITG mode travelling in the ion diamagnetic direction, i.e. $\omega \omega _{*i}>0$
as the ratio between the temperature and density gradients (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander et al. Reference Helander, Proll and Plunk2013). For a typical ITG mode travelling in the ion diamagnetic direction, i.e. $\omega \omega _{*i}>0$![]() , and as long as $0 \leq \eta _e<2/3$
, and as long as $0 \leq \eta _e<2/3$![]() , i.e. the electron temperature gradient is not too large compared with the density gradient, the energy transfer rate of the electrons will always be positive, $P_e>0$
, i.e. the electron temperature gradient is not too large compared with the density gradient, the energy transfer rate of the electrons will always be positive, $P_e>0$![]() , meaning the electrons will draw energy from the mode rather than provide it. This finding does not only hold for maximum-${\rm J}$
, meaning the electrons will draw energy from the mode rather than provide it. This finding does not only hold for maximum-${\rm J}$![]() configurations but is, in fact, independent of any details of the geometry. This is perhaps a rather trivial finding when we only consider two species: to reach the point of marginal stability, where the sum of the energy transfer rates must be zero, only one species can provide the drive while the other will have to draw energy from the instability, and it is no surprise that the ions would be found to provide the drive for an ITG and the electrons to be stabilising. However, the result is also valid for more than two species, i.e. the stabilising property of the electrons remains even in situations with impurity species.
configurations but is, in fact, independent of any details of the geometry. This is perhaps a rather trivial finding when we only consider two species: to reach the point of marginal stability, where the sum of the energy transfer rates must be zero, only one species can provide the drive while the other will have to draw energy from the instability, and it is no surprise that the ions would be found to provide the drive for an ITG and the electrons to be stabilising. However, the result is also valid for more than two species, i.e. the stabilising property of the electrons remains even in situations with impurity species.
Far from marginality, we can still show that electrons are stabilising for ITGs in maximum-${\rm J}$![]() configurations: as described by Plunk, Connor & Helander (Reference Plunk, Connor and Helander2017), in the strongly driven limit,
configurations: as described by Plunk, Connor & Helander (Reference Plunk, Connor and Helander2017), in the strongly driven limit,
which applies when gradients are large (and thus far from marginality), the dispersion relation of electrostatic modes can be cast into the form
with
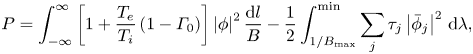


where we have defined the bounce averages of the potential $\phi$![]() and the electron drift frequency $\omega _{de}$
and the electron drift frequency $\omega _{de}$![]() within a trapping well $j$
within a trapping well $j$![]() with magnetic field strength $B < 1/\lambda$
with magnetic field strength $B < 1/\lambda$![]() in the following form:
in the following form:

where $\tau _j$![]() denotes the bounce time. For the integral over all trapped particles, we then need to sum over all possible trapping wells $j$
denotes the bounce time. For the integral over all trapped particles, we then need to sum over all possible trapping wells $j$![]() for a given pitch angle $\lambda$
for a given pitch angle $\lambda$![]() .
.
In the derivation of this dispersion relation, ion motion along the magnetic field has been neglected, which excludes slab ITG modes from the consideration but includes the curvature-driven ITG mode. While $P$![]() can be shown to be positive definite (Helander et al. Reference Helander, Proll and Plunk2013), $Q$
can be shown to be positive definite (Helander et al. Reference Helander, Proll and Plunk2013), $Q$![]() and $R$
and $R$![]() can have either sign. Importantly, from (2.5), we see that we require $4PR>Q^2$
can have either sign. Importantly, from (2.5), we see that we require $4PR>Q^2$![]() for $\omega$
for $\omega$![]() having an imaginary part and thus an instability to exist. With $P$
having an imaginary part and thus an instability to exist. With $P$![]() positive, only a positive $R$
positive, only a positive $R$![]() can lead to an instability, and a larger $R$
can lead to an instability, and a larger $R$![]() would mean a more unstable instability. As argued by Plunk et al. (Reference Plunk, Connor and Helander2017), the electron contribution to $R$
would mean a more unstable instability. As argued by Plunk et al. (Reference Plunk, Connor and Helander2017), the electron contribution to $R$![]() , i.e. the second term, is negative and thus stabilising for all $\eta _e \geq -1$
, i.e. the second term, is negative and thus stabilising for all $\eta _e \geq -1$![]() , due to the proportionality to $\omega _{*e}\bar {\omega }_{dej}$
, due to the proportionality to $\omega _{*e}\bar {\omega }_{dej}$![]() , which is negative for all particle orbits in maximum-${\rm J}$
, which is negative for all particle orbits in maximum-${\rm J}$![]() devices. Only the ion contribution, i.e. the first term in $R$
devices. Only the ion contribution, i.e. the first term in $R$![]() , can be destabilising. Note that this form implies that stabilisation is expected from both the electron temperature and density gradients in the strongly driven limit.
, can be destabilising. Note that this form implies that stabilisation is expected from both the electron temperature and density gradients in the strongly driven limit.
These arguments thus predict enhanced stability of maximum-${\rm J}$![]() configurations also to toroidal ITG modes, as soon as a density gradient is present, and thus add to the prediction of enhanced stability to TEMs shown analytically linearly (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander et al. Reference Helander, Proll and Plunk2013) and nonlinearly (Helander Reference Helander2017). The nonlinear argument in fact also extends to ITGs, as it can be shown that less energy (in the electrons) is available to drive instabilities when the density profile is slightly peaked than when it is flat (Helander Reference Helander2020). Although they are not immune to ITG modes, maximum-${\rm J}$
configurations also to toroidal ITG modes, as soon as a density gradient is present, and thus add to the prediction of enhanced stability to TEMs shown analytically linearly (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander et al. Reference Helander, Proll and Plunk2013) and nonlinearly (Helander Reference Helander2017). The nonlinear argument in fact also extends to ITGs, as it can be shown that less energy (in the electrons) is available to drive instabilities when the density profile is slightly peaked than when it is flat (Helander Reference Helander2020). Although they are not immune to ITG modes, maximum-${\rm J}$![]() devices should thus benefit from somewhat reduced turbulence over a large range of parameter space, whenever a density gradient is present. In the absence of any electron drive, i.e. for flat density and electron temperature gradients, the presence of trapped electrons (second term in $P$
devices should thus benefit from somewhat reduced turbulence over a large range of parameter space, whenever a density gradient is present. In the absence of any electron drive, i.e. for flat density and electron temperature gradients, the presence of trapped electrons (second term in $P$![]() ) will deplete the Boltzmann electron density response. This will reduce $P$
) will deplete the Boltzmann electron density response. This will reduce $P$![]() and thus increase the growth rate of the ITG (see (2.5)), as will be seen when comparing ITG simulations with adiabatic and kinetic electrons.
and thus increase the growth rate of the ITG (see (2.5)), as will be seen when comparing ITG simulations with adiabatic and kinetic electrons.
3. Simulation set-up
Collisionless electrostatic simulations were performed with the flux-tube version of the Eulerian code GENE (Jenko et al. Reference Jenko, Dorland, Kotschenreuther and Rogers2000, see genecode.org for code details and access), which solves the gyrokinetic equation together with Maxwell's equations and incorporates realistic geometry when coupled to the GIST code (Xanthopoulos et al. Reference Xanthopoulos, Cooper, Jenko, Turkin, Runov and Geiger2009). For W7-X and HSX, the flux tubes studied cross the outboard midplane in the bean-shaped cross-section of the stellarator at the midpoint of the flux tube, as these flux tubes have been found to be the most unstable ones to ITG modes and TEMs in previous studies (Proll et al. Reference Proll, Xanthopoulos and Helander2013; Faber et al. Reference Faber, Pueschel, Proll, Xanthopoulos, Terry, Hegna, Weir, Likin and Talmadge2015). While for W7-X, one poloidal turn has found to be sufficient for convergence, for HSX 4,poloidal turns have been found to be necessary (Faber et al. Reference Faber, Pueschel, Terry, Hegna and Roman2018). In all three devices, the flux surface chosen was at half-normalised toroidal flux, i.e. $s=\psi /\psi _0=0.5$![]() . For more information about the geometry, the reader is referred to Proll et al. (Reference Proll, Xanthopoulos and Helander2013) for DIII-D and W7-X and to Faber et al. (Reference Faber, Pueschel, Terry, Hegna and Roman2018) for HSX. ITG turbulence was modelled with both adiabatic (ITG-ae) and kinetic (ITG-ke) electrons, and TEM with a pure density gradient; the resolution was chosen as seen in table 1. There, $nz$
. For more information about the geometry, the reader is referred to Proll et al. (Reference Proll, Xanthopoulos and Helander2013) for DIII-D and W7-X and to Faber et al. (Reference Faber, Pueschel, Terry, Hegna and Roman2018) for HSX. ITG turbulence was modelled with both adiabatic (ITG-ae) and kinetic (ITG-ke) electrons, and TEM with a pure density gradient; the resolution was chosen as seen in table 1. There, $nz$![]() refers to the number of grid points along a field line, $nkx$
refers to the number of grid points along a field line, $nkx$![]() the number of grid points in the radial direction, $nky$
the number of grid points in the radial direction, $nky$![]() to the number of Fourier modes in the binormal direction (i.e. perpendicular to both the field line and the radial direction), $nv$
to the number of Fourier modes in the binormal direction (i.e. perpendicular to both the field line and the radial direction), $nv$![]() to the number of grid points in the direction of parallel velocity $v_{\|}$
to the number of grid points in the direction of parallel velocity $v_{\|}$![]() , $nw$
, $nw$![]() to that in the direction of the magnetic moment $\mu$
to that in the direction of the magnetic moment $\mu$![]() and $\mathrm {kymin}$
and $\mathrm {kymin}$![]() to the minimum value of the wavenumber in units of inverse gyroradius.
to the minimum value of the wavenumber in units of inverse gyroradius.
Table 1. Resolution for turbulence simulations (nkx, nky, nz, nv, nw, kymin) for ITGs with adiabatic (ITG-ae) and kinetic (ITG-ke) electrons and TEM with a pure density gradient.

For TEMs in HSX, $k_y \rho _s =0.1$![]() was found to be sufficient as the smallest binormal wavenumber. The simulations are performed with a realistic mass ratio for hydrogen plasmas of $m_e/m_i=1/1836$
was found to be sufficient as the smallest binormal wavenumber. The simulations are performed with a realistic mass ratio for hydrogen plasmas of $m_e/m_i=1/1836$![]() and a temperature ratio of $T_e/T_i=1$
and a temperature ratio of $T_e/T_i=1$![]() ,Footnote 1 where $m_{e}$
,Footnote 1 where $m_{e}$![]() and $m_{i}$
and $m_{i}$![]() are the electron mass and the ion mass, respectively, and $T_{e}$
are the electron mass and the ion mass, respectively, and $T_{e}$![]() and $T_{i}$
and $T_{i}$![]() the electron and ion temperatures, respectively. To assess the relative strength of the turbulence in different devices and for different types of drive, we will compare the sum of the electrostatic heat fluxes for both species $s$
the electron and ion temperatures, respectively. To assess the relative strength of the turbulence in different devices and for different types of drive, we will compare the sum of the electrostatic heat fluxes for both species $s$![]() , $Q=\sum _s Q_s$
, $Q=\sum _s Q_s$![]() , and the particle flux $\varGamma =\varGamma _e=\varGamma _i$
, and the particle flux $\varGamma =\varGamma _e=\varGamma _i$![]() , defined as follows:
, defined as follows:
with $f_{s,1}$![]() as the fluctuating part of the particle distribution function of species $s$
as the fluctuating part of the particle distribution function of species $s$![]() , ${v}_{d,r}$
, ${v}_{d,r}$![]() is approximated by the radial component of the generalised $\boldsymbol {E}\times \boldsymbol {B}$
is approximated by the radial component of the generalised $\boldsymbol {E}\times \boldsymbol {B}$![]() velocity, $m_s$
velocity, $m_s$![]() is the particle mass and where $\langle \cdots \rangle$
is the particle mass and where $\langle \cdots \rangle$![]() denotes the average over the flux tube. Both fluxes are normalised to gyro-Bohm units,
denotes the average over the flux tube. Both fluxes are normalised to gyro-Bohm units,
with ion density $n_i$![]() , ion temperature $T_i$
, ion temperature $T_i$![]() , ion mass $m_i$
, ion mass $m_i$![]() , minor radius $a$
, minor radius $a$![]() and ion gyro frequency $\varOmega _i$
and ion gyro frequency $\varOmega _i$![]() typically evaluated at the magnetic axis. In this formulation, differences in surface-to-volume ratio are not accounted for. To compensate for that, factors of $5$
typically evaluated at the magnetic axis. In this formulation, differences in surface-to-volume ratio are not accounted for. To compensate for that, factors of $5$![]() or $4$
or $4$![]() for W7-X or HSX, respectively, would have to be used when comparing against DIII-D. For the linear simulations, we typically scan over the binormal wavenumber $k_y \rho _s$
for W7-X or HSX, respectively, would have to be used when comparing against DIII-D. For the linear simulations, we typically scan over the binormal wavenumber $k_y \rho _s$![]() , where $\rho _s=\sqrt {T_i/m_i}/\varOmega _i$
, where $\rho _s=\sqrt {T_i/m_i}/\varOmega _i$![]() , and we use the radial mode number $k_x \rho _s=0$
, and we use the radial mode number $k_x \rho _s=0$![]() .
.
4. Nonlinear simulation results
4.1. Ion-temperature-gradient (ITG) modes
First, we study the effect of the magnetic geometry on ITG turbulence by varying the ion temperature gradient $a/L_{T_i}=- a\,\mathrm {d}\ln T_i/\mathrm {d}r$![]() while setting the electron-temperature gradient and the density gradient to zero. It is found that the heat flux of turbulence resulting from ITGs with adiabatic electrons (ITG-ae) is smaller in both stellarators than in DIII-D, see figure 1. The difference can likely be attributed to the strong local shear and low global shear in both stellarator devices (Plunk et al. Reference Plunk, Helander, Xanthopoulos and Connor2014) – with HSX having particularly low global shear, also compare McKinney et al. (Reference McKinney, Pueschel, Faber, Hegna, Talmadge, Anderson, Mynick and Xanthopoulos2019) – as well as generally smaller local curvature in W7-X. This difference is also reflected in the linear growth rates (for W7-X and DIII-D, see Proll et al. Reference Proll, Xanthopoulos and Helander2013). If we now add a density gradient $a/L_n=1$
while setting the electron-temperature gradient and the density gradient to zero. It is found that the heat flux of turbulence resulting from ITGs with adiabatic electrons (ITG-ae) is smaller in both stellarators than in DIII-D, see figure 1. The difference can likely be attributed to the strong local shear and low global shear in both stellarator devices (Plunk et al. Reference Plunk, Helander, Xanthopoulos and Connor2014) – with HSX having particularly low global shear, also compare McKinney et al. (Reference McKinney, Pueschel, Faber, Hegna, Talmadge, Anderson, Mynick and Xanthopoulos2019) – as well as generally smaller local curvature in W7-X. This difference is also reflected in the linear growth rates (for W7-X and DIII-D, see Proll et al. Reference Proll, Xanthopoulos and Helander2013). If we now add a density gradient $a/L_n=1$![]() for the case with $a/L_{T_i}=3$
for the case with $a/L_{T_i}=3$![]() , we see the typical (Coppi, Rosenbluth & Sagdeev Reference Coppi, Rosenbluth and Sagdeev1967) partial stabilisation of ITG through the density gradient, resulting in reduced heat fluxes in all three devices.
, we see the typical (Coppi, Rosenbluth & Sagdeev Reference Coppi, Rosenbluth and Sagdeev1967) partial stabilisation of ITG through the density gradient, resulting in reduced heat fluxes in all three devices.

Figure 1. ITG adiabatic electrons: Flux-tube-averaged and time-averaged (in the quasi-stationary phase) normalised heat fluxes in W7-X, HSX and DIII-D for ion-temperature-gradient-driven turbulence with adiabatic electrons. The full symbols show how the heat fluxes change for an ion-temperature gradient of $a/L_{T_i}=3$![]() once a small density gradient $a/L_n=1$
once a small density gradient $a/L_n=1$![]() is present.
is present.
Returning to the scenario with a flat density profile, the aforementioned inter-machine trend changes significantly if we also consider kinetic electrons: Initially we note that with kinetic electrons, the relative magnitude of the fluxes – now also the particle flux in addition to the heat flux, see figure 2 – between the devices remains similar, with DIII-D having the highest fluxes and W7-X having the lowest (even though the particle fluxes of HSX are only barely larger than those of W7-X), and that all heat fluxes have increased compared with the case of adiabatic electrons, with the increase being strongest for HSX and weakest for W7-X. This increase in ITG activity when going from adiabatic to kinetic electrons is also observed in the linear growth rates and was discussed above. Now, if again a density gradient $a/L_n=1$![]() is added for the case with kinetic electrons and an ion-temperature gradient $a/L_{T_i}=3$
is added for the case with kinetic electrons and an ion-temperature gradient $a/L_{T_i}=3$![]() , we observe that the three devices behave very differently: for DIII-D, both the heat flux and the particle flux increase strongly. This can be explained by trapped-electron-modes being destabilised (as is also seen in the linear growth rates, see figure 3), which then contribute to both fluxes. In W7-X and HSX, we see the opposite behaviour: the particle fluxes remain nearly constant, and the heat fluxes even decrease. This is rather remarkable, and to understand it, one needs to consider the linear growth rates for the ITGs with and without a density gradient, see figure 3. In W7-X, we see a reduction in linear growth rates once a density gradient is present, but not in DIII-D or in HSX. We attribute this to the high degree of maximum-${\rm J}$
, we observe that the three devices behave very differently: for DIII-D, both the heat flux and the particle flux increase strongly. This can be explained by trapped-electron-modes being destabilised (as is also seen in the linear growth rates, see figure 3), which then contribute to both fluxes. In W7-X and HSX, we see the opposite behaviour: the particle fluxes remain nearly constant, and the heat fluxes even decrease. This is rather remarkable, and to understand it, one needs to consider the linear growth rates for the ITGs with and without a density gradient, see figure 3. In W7-X, we see a reduction in linear growth rates once a density gradient is present, but not in DIII-D or in HSX. We attribute this to the high degree of maximum-${\rm J}$![]() property of W7-X, which leads to a large fraction of trapped electrons having favourable curvature and thus being stabilising, as discussed above. An alternate explanation (Kotschenreuther et al. Reference Kotschenreuther, Liu, Hatch, Mahajan, Pueschel, Halfmoon, Zarnstorff, Garofalo, McClenaghan, McKinney and Qian2020) involves enhanced electron adiabaticity; assessing the relative effectiveness of these mechanisms is beyond the scope of the present work. As this reduction in growth rates is only seen at low wavenumbers ($k_y \rho _{s} \approx 0.1\text {--}0.2$
property of W7-X, which leads to a large fraction of trapped electrons having favourable curvature and thus being stabilising, as discussed above. An alternate explanation (Kotschenreuther et al. Reference Kotschenreuther, Liu, Hatch, Mahajan, Pueschel, Halfmoon, Zarnstorff, Garofalo, McClenaghan, McKinney and Qian2020) involves enhanced electron adiabaticity; assessing the relative effectiveness of these mechanisms is beyond the scope of the present work. As this reduction in growth rates is only seen at low wavenumbers ($k_y \rho _{s} \approx 0.1\text {--}0.2$![]() ), the effect may be insufficient in fully explaining the reduction in nonlinear heat flux. However, to properly appreciate the linear effect of the maximum-J property, one needs to contrast the mild stabilisation of W7-X with the robust destabilisation for all wavenumbers in HSX, as expected when the TEM drive is increased, discussed immediately hereafter. Thus, one may conclude that the response of the heat flux of W7-X to increased density gradient indeed benefits from the stabilising influence of the maximum-J property.
), the effect may be insufficient in fully explaining the reduction in nonlinear heat flux. However, to properly appreciate the linear effect of the maximum-J property, one needs to contrast the mild stabilisation of W7-X with the robust destabilisation for all wavenumbers in HSX, as expected when the TEM drive is increased, discussed immediately hereafter. Thus, one may conclude that the response of the heat flux of W7-X to increased density gradient indeed benefits from the stabilising influence of the maximum-J property.
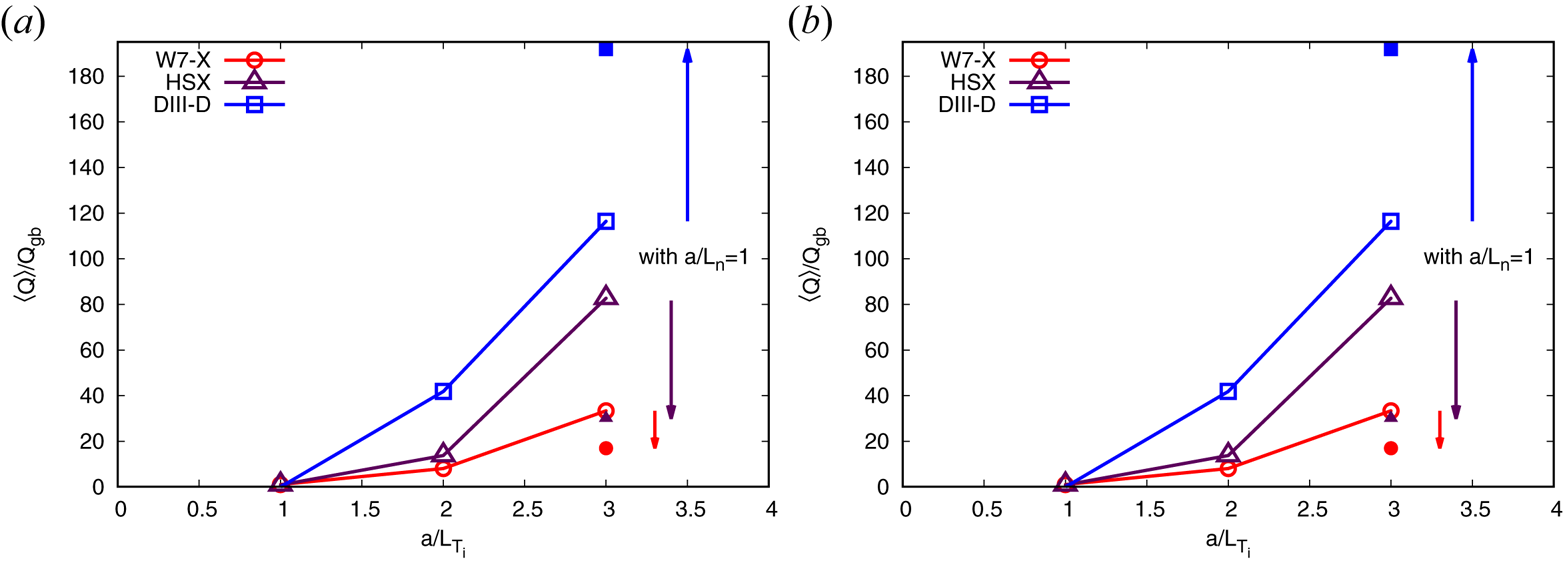
Figure 2. ITG kinetic electrons: flux-tube-averaged and time-averaged (in the quasi-stationary phase) normalised heat fluxes (a) and particle fluxes (b) in W7-X, HSX and DIII-D for ion-temperature-gradient-driven turbulence with kinetic electrons. The full symbols show how the fluxes change for an ion-temperature gradient of $a/L_{T_i}=3$![]() once a small density gradient $a/L_n=1$
once a small density gradient $a/L_n=1$![]() is present.
is present.
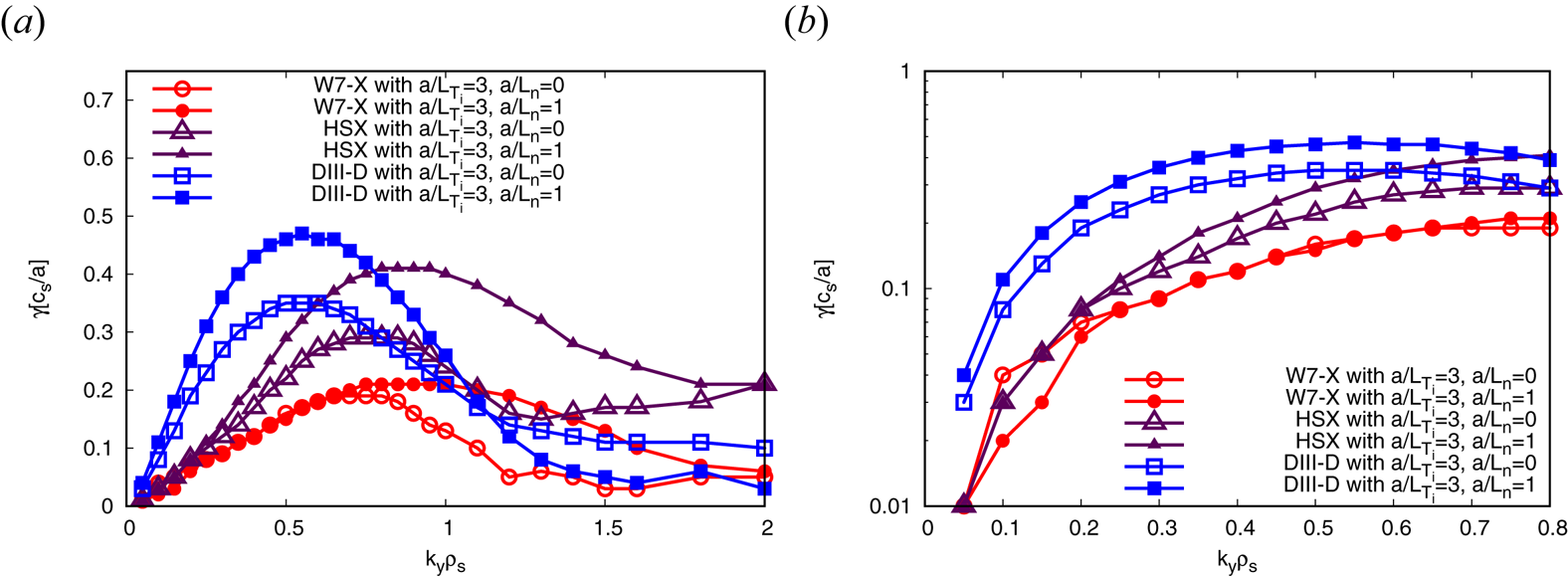
Figure 3. Normalised growth rates $\gamma$![]() of ITGs with kinetic electrons (ITG-ke) at $a/L_{T_i}=3$
of ITGs with kinetic electrons (ITG-ke) at $a/L_{T_i}=3$![]() with (full symbols) and without (open symbols) added density gradient of $a/L_n=1$
with (full symbols) and without (open symbols) added density gradient of $a/L_n=1$![]() in W7-X, HSX and DIII-D, for a large range of wavenumbers (a) and only the small wavenumbers (b).
in W7-X, HSX and DIII-D, for a large range of wavenumbers (a) and only the small wavenumbers (b).
In HSX, no linear stabilisation is observed but rather a destabilisation like in DIII-D, which is very well understandable as HSX is far from maximum-${\rm J}$![]() . However, the nonlinear heat and particle fluxes show the opposite behaviour and decrease or remain constant, respectively, rather than increase, just like in W7-X. We thus note that in HSX, a strong nonlinearly stabilising mechanism exists in the form of enhanced energy transfer to stable eigenmodes (Hegna, Terry & Faber Reference Hegna, Terry and Faber2018; Terry et al. Reference Terry, Faber, Hegna, Mirnov, Pueschel and Whelan2018), as measured, e.g. by the triplet correlation time (Terry et al. Reference Terry, Faber, Hegna, Mirnov, Pueschel and Whelan2018; Whelan, Pueschel & Terry Reference Whelan, Pueschel and Terry2018; Li et al. Reference Li, Terry, Whelan and Pueschel2021; Pueschel, Li & Terry Reference Pueschel, Li and Terry2021). The process underlying the substantial nonlinear stabilisation observed in HSX is likely also at work in W7-X, though to a smaller degree due to, among other factors, the differences in magnetic shear. The delicate task of evaluating the relative importance of the linear and nonlinear stabilisation will be left for future work. We note the possibility that both effects may be exploited in future stellarator designs.
. However, the nonlinear heat and particle fluxes show the opposite behaviour and decrease or remain constant, respectively, rather than increase, just like in W7-X. We thus note that in HSX, a strong nonlinearly stabilising mechanism exists in the form of enhanced energy transfer to stable eigenmodes (Hegna, Terry & Faber Reference Hegna, Terry and Faber2018; Terry et al. Reference Terry, Faber, Hegna, Mirnov, Pueschel and Whelan2018), as measured, e.g. by the triplet correlation time (Terry et al. Reference Terry, Faber, Hegna, Mirnov, Pueschel and Whelan2018; Whelan, Pueschel & Terry Reference Whelan, Pueschel and Terry2018; Li et al. Reference Li, Terry, Whelan and Pueschel2021; Pueschel, Li & Terry Reference Pueschel, Li and Terry2021). The process underlying the substantial nonlinear stabilisation observed in HSX is likely also at work in W7-X, though to a smaller degree due to, among other factors, the differences in magnetic shear. The delicate task of evaluating the relative importance of the linear and nonlinear stabilisation will be left for future work. We note the possibility that both effects may be exploited in future stellarator designs.
4.2. Trapped-electron modes (TEM)
To study density-gradient-driven TEMs, both temperature gradients are set to zero and only the density gradient is varied. The heat and particle fluxes in both stellarators are up to two orders of magnitude smaller than that in the DIII-D geometry (see figure 4). In W7-X, the explanation for the low fluxes lies again with the high degree of maximum-${\rm J}$![]() property: not only are the linear growth rates of the density-gradient-driven TEM much smaller than in the two other devices (figure 5) – as predicted (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander et al. Reference Helander, Proll and Plunk2013)– but we conclude that the enhanced stability also holds nonlinearly. One surprising observation is that in W7-X, the fluxes at $a/L_n=1$
property: not only are the linear growth rates of the density-gradient-driven TEM much smaller than in the two other devices (figure 5) – as predicted (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander et al. Reference Helander, Proll and Plunk2013)– but we conclude that the enhanced stability also holds nonlinearly. One surprising observation is that in W7-X, the fluxes at $a/L_n=1$![]() are slightly larger than those at $a/L_n=2$
are slightly larger than those at $a/L_n=2$![]() (figure 4). This cannot be explained by the difference in linear growth rates (figure 6), which increase monotonically with increasing density gradient, as expected. We do, however, observe distinctly different modes at large perpendicular scales ($k_y\rho _s \leq 0.5$
(figure 4). This cannot be explained by the difference in linear growth rates (figure 6), which increase monotonically with increasing density gradient, as expected. We do, however, observe distinctly different modes at large perpendicular scales ($k_y\rho _s \leq 0.5$![]() with $k_x\rho _s=0)$
with $k_x\rho _s=0)$![]() ): for both $a/L_n=2$
): for both $a/L_n=2$![]() and $a/L_n=3$
and $a/L_n=3$![]() , the modes at these large scales propagate in the electron diamagnetic direction and have recently been classified as ‘Universal instabilities’ (Cheng & Chen Reference Cheng and Chen1980; Chowdhury et al. Reference Chowdhury, Ganesh, Brunner, Vaclavik and Villard2010; Helander & Plunk Reference Helander and Plunk2015; Landreman, Antonsen & Dorland Reference Landreman, Antonsen and Dorland2015a; Landreman, Plunk & Dorland Reference Landreman, Plunk and Dorland2015b; Costello, Proll & Plunk Reference Costello, Proll and Plunk2021), while the mode that is seen at smaller scales in all cases, but that also dominates the large scales at $a/L_n=1$
, the modes at these large scales propagate in the electron diamagnetic direction and have recently been classified as ‘Universal instabilities’ (Cheng & Chen Reference Cheng and Chen1980; Chowdhury et al. Reference Chowdhury, Ganesh, Brunner, Vaclavik and Villard2010; Helander & Plunk Reference Helander and Plunk2015; Landreman, Antonsen & Dorland Reference Landreman, Antonsen and Dorland2015a; Landreman, Plunk & Dorland Reference Landreman, Plunk and Dorland2015b; Costello, Proll & Plunk Reference Costello, Proll and Plunk2021), while the mode that is seen at smaller scales in all cases, but that also dominates the large scales at $a/L_n=1$![]() , propagates in the ion diamagnetic direction and is most likely the ion-driven trapped electron mode (iTEM) described by Plunk et al. (Reference Plunk, Connor and Helander2017). Both types of mode may have different nonlinear properties and therefore lead to differences in saturated amplitude. For HSX, understanding the low heat flux requires taking into account nonlinear saturation mechanisms. Just as for the ITG simulations with a density gradient present, the growth rates are much higher than in W7-X due to the lack of the maximum-${\rm J}$
, propagates in the ion diamagnetic direction and is most likely the ion-driven trapped electron mode (iTEM) described by Plunk et al. (Reference Plunk, Connor and Helander2017). Both types of mode may have different nonlinear properties and therefore lead to differences in saturated amplitude. For HSX, understanding the low heat flux requires taking into account nonlinear saturation mechanisms. Just as for the ITG simulations with a density gradient present, the growth rates are much higher than in W7-X due to the lack of the maximum-${\rm J}$![]() property. Even though the TEMs in HSX have shorter wavelengths than in DIII-D, a simple quasi-linear theory or mixing-length estimate cannot explain why the heat flux in HSX is comparable to, or even smaller than, that in W7-X. However, at very low background magnetic shear as in HSX, nonlinear energy transfer to stable eigenmodes can be enhanced, leading to lower-than-expected heat flux. Note that similar nonlinearly stabilising features have been seen in ITG turbulence comparisons between HSX and an axisymmetric configuration (McKinney et al. Reference McKinney, Pueschel, Faber, Hegna, Talmadge, Anderson, Mynick and Xanthopoulos2019). One final observation regarding W7-X is that, in spite of the TEM heat flux being small compared with the ITG heat flux or the heat fluxes in DIII-D, it is still large compared with the neoclassical flux as calculated by the SFINCS code (Landreman et al. Reference Landreman, Smith, Mollén and Helander2014) at typical values of density $n=10^{19}\,{\rm m}^{-3}$
property. Even though the TEMs in HSX have shorter wavelengths than in DIII-D, a simple quasi-linear theory or mixing-length estimate cannot explain why the heat flux in HSX is comparable to, or even smaller than, that in W7-X. However, at very low background magnetic shear as in HSX, nonlinear energy transfer to stable eigenmodes can be enhanced, leading to lower-than-expected heat flux. Note that similar nonlinearly stabilising features have been seen in ITG turbulence comparisons between HSX and an axisymmetric configuration (McKinney et al. Reference McKinney, Pueschel, Faber, Hegna, Talmadge, Anderson, Mynick and Xanthopoulos2019). One final observation regarding W7-X is that, in spite of the TEM heat flux being small compared with the ITG heat flux or the heat fluxes in DIII-D, it is still large compared with the neoclassical flux as calculated by the SFINCS code (Landreman et al. Reference Landreman, Smith, Mollén and Helander2014) at typical values of density $n=10^{19}\,{\rm m}^{-3}$![]() and temperature $T=1\text {--}5\,\mathrm {keV}$
and temperature $T=1\text {--}5\,\mathrm {keV}$![]() (see figure 7). This clearly supports turbulent transport as the dominant transport channel in W7-X, and is very much in line with the experimental observations (Dinklage et al. Reference Dinklage, Beidler, Helander, Fuchert, Maaberg, Rahbarnia, Sunn Pedersen, Turkin, Wolf and Andreeva2018), where it was found that the heat flux calculated by neoclassical theory is not sufficient to explain experimental measurements.
(see figure 7). This clearly supports turbulent transport as the dominant transport channel in W7-X, and is very much in line with the experimental observations (Dinklage et al. Reference Dinklage, Beidler, Helander, Fuchert, Maaberg, Rahbarnia, Sunn Pedersen, Turkin, Wolf and Andreeva2018), where it was found that the heat flux calculated by neoclassical theory is not sufficient to explain experimental measurements.
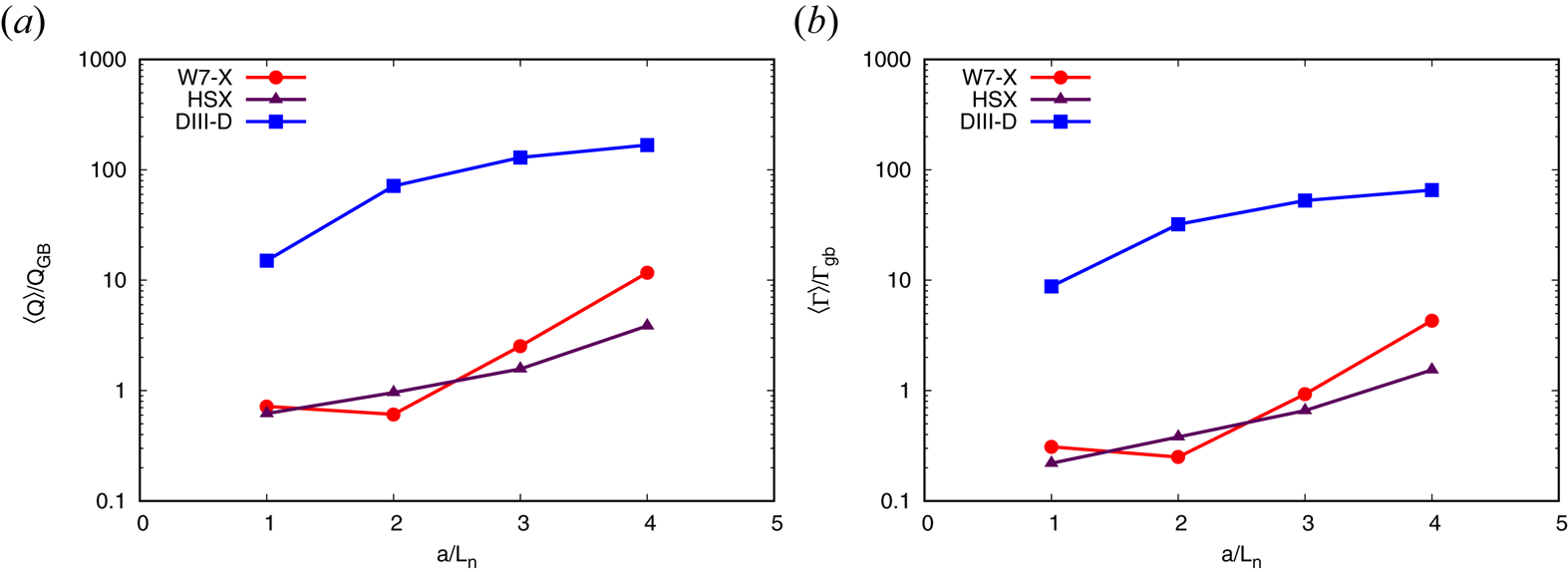
Figure 4. TEM: flux-tube-averaged and time-averaged (in the quasi-stationary phase) normalised heat fluxes (a) and particle fluxes (b) in W7-X, HSX and DIII-D for density-gradient-driven turbulence with kinetic electrons.
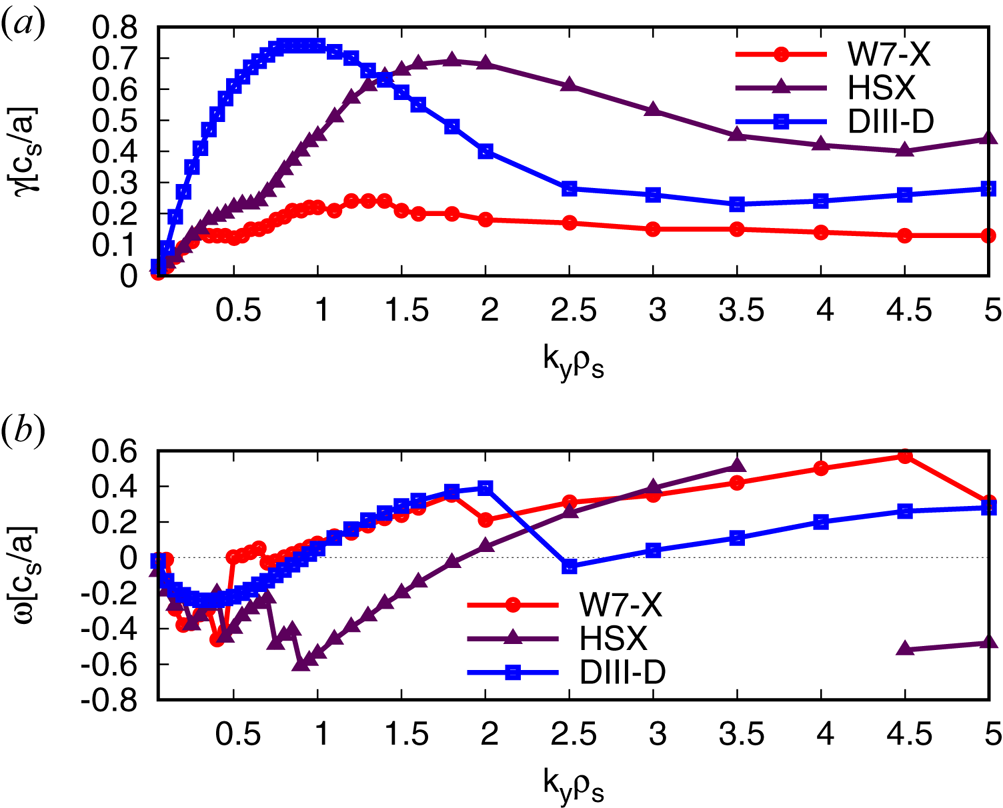
Figure 5. Normalised growth rates $\gamma$![]() and real frequencies $\omega$
and real frequencies $\omega$![]() of density-gradient-driven modes in W7-X, HSX and DIII-D for $a/L_{n}=3$
of density-gradient-driven modes in W7-X, HSX and DIII-D for $a/L_{n}=3$![]() .
.
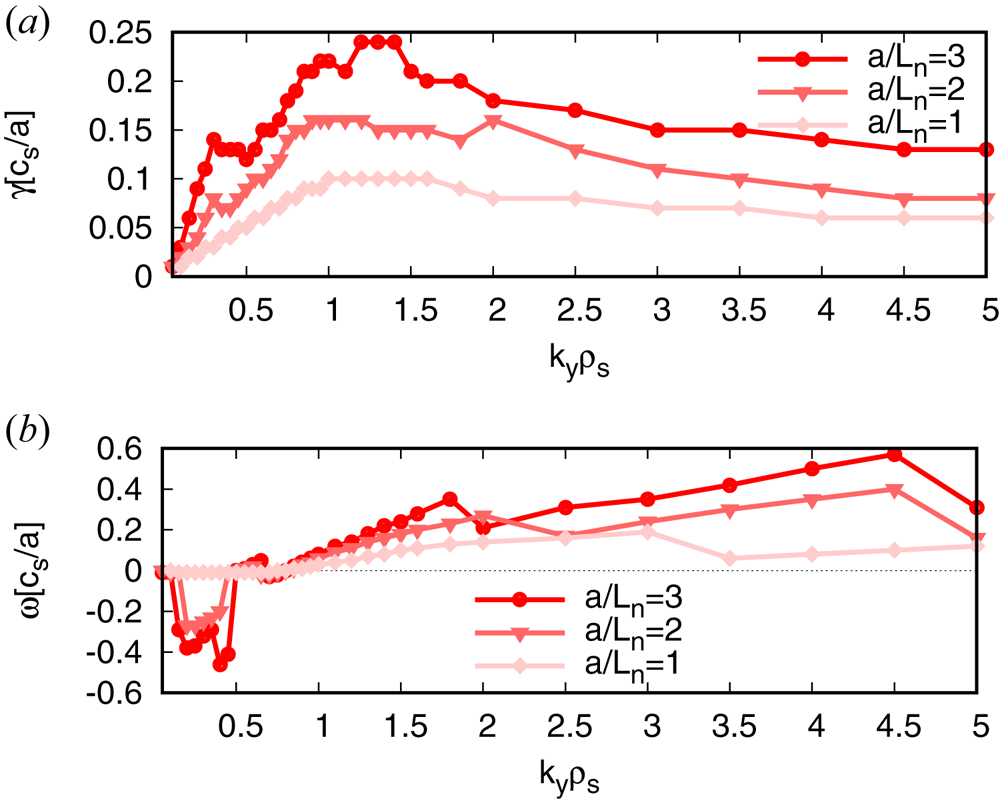
Figure 6. Normalised growth rates $\gamma$![]() and real frequencies $\omega$
and real frequencies $\omega$![]() for density gradients $a/L_{n}=1,2,3$
for density gradients $a/L_{n}=1,2,3$![]() in W7-X.
in W7-X.
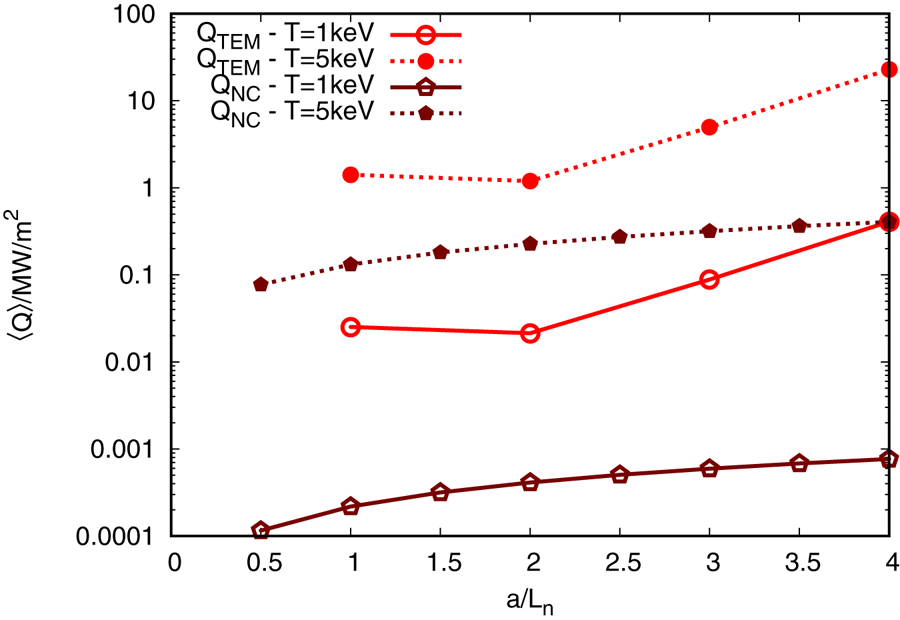
Figure 7. TEM turbulent heat flux $Q_{TEM}$![]() (red circles) and neoclassical heat flux $Q_{NC}$
(red circles) and neoclassical heat flux $Q_{NC}$![]() (maroon pentagons), respectively, in W7-X for different density gradients. The usual normalisation in gyro-Bohm units has been transformed into ${\rm MW}\,{\rm m}^{-2}$
(maroon pentagons), respectively, in W7-X for different density gradients. The usual normalisation in gyro-Bohm units has been transformed into ${\rm MW}\,{\rm m}^{-2}$![]() , assuming a density of $n=5 \times 10^{19}\,{\rm m}^{-3}$
, assuming a density of $n=5 \times 10^{19}\,{\rm m}^{-3}$![]() and temperatures of $T = 1\,\mathrm {keV}$
and temperatures of $T = 1\,\mathrm {keV}$![]() and $T = 5\,\mathrm {keV}$
and $T = 5\,\mathrm {keV}$![]() .
.
In summary, we find that in W7-X, the turbulent heat flux of both density-gradient-driven TEM and ITGs with a small density gradient is much lower than in a tokamak geometry. We attribute this enhanced stability to the maximum-${\rm J}$![]() property of W7-X, though also enhanced electron adiabaticity (Kotschenreuther et al. Reference Kotschenreuther, Liu, Hatch, Mahajan, Pueschel, Halfmoon, Zarnstorff, Garofalo, McClenaghan, McKinney and Qian2020) cannot be ruled out as a possible explanation. HSX seems to benefit from a more powerful saturation mechanism, despite lacking maximum-${\rm J}$
property of W7-X, though also enhanced electron adiabaticity (Kotschenreuther et al. Reference Kotschenreuther, Liu, Hatch, Mahajan, Pueschel, Halfmoon, Zarnstorff, Garofalo, McClenaghan, McKinney and Qian2020) cannot be ruled out as a possible explanation. HSX seems to benefit from a more powerful saturation mechanism, despite lacking maximum-${\rm J}$![]() optimisation. This suggests that turbulence in stellarators like W7-X or HSX can be mitigated by increasing the density gradient, for example, through pellet injection, as recently reported for W7-X (Bozhenkov et al. Reference Bozhenkov, Kazakov, Ford, Beurskens, Alcusón, Alonso, Baldzuhn, Brandt, Brunner and Damm2020), thus providing a path toward enhanced fusion performance.
optimisation. This suggests that turbulence in stellarators like W7-X or HSX can be mitigated by increasing the density gradient, for example, through pellet injection, as recently reported for W7-X (Bozhenkov et al. Reference Bozhenkov, Kazakov, Ford, Beurskens, Alcusón, Alonso, Baldzuhn, Brandt, Brunner and Damm2020), thus providing a path toward enhanced fusion performance.
Acknowledgements
The authors would like to thank the GENE team – most notably D. Told, F. Jenko, H. Doerk and A. Bañón-Navarro – for their efforts and support. We would also like to thank G. Hammett, S. Lazerson, H. Mynick, J. Citrin and M. Kotschenreuther for lots of stimulating and helpful discussions. The simulations were performed on MPCDFs Hydra and Helios at IFERC-CSC.
Editor William Dorland thanks the referees for their advice in evaluating this article.
Funding
This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 and 2019–2020 under grant agreement No. 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission.
Declaration of interests
The authors report no conflict of interest.






























