Introduction
This is the second overview paper on the use of Monte-Carlo in radiotherapy. The first part gave an introduction to the Monte-Carlo technique and the different codes that are available for simulating radiotherapy treatments. In this second overview paper on the use of Monte-Carlo for radiotherapy, the main areas of application will be summarised. This includes modelling the production of beams of ionising radiation for radiotherapy and medical imaging, treatment verification, patient dosimetry and radiobiology.
Radiotherapy and imaging equipment modelling
A common application of the Monte-Carlo method is in the modelling of imaging and radiotherapy equipment such as X-ray tubes, linear accelerators and detectors. For comprehensive reviews of the use of Monte-Carlo techniques for radiotherapy, the reader is referred to the following literature. Reference Verhaegen and Seuntjens1–Reference Verhaegen and Seco9 An overview of some of the published work in some of the different areas of radiotherapy now follows.
X-ray tube modelling
Monte-Carlo techniques have been used to model X-ray tubes in the context of kilo- and ortho-voltage radiotherapy as well as medical and industrial imaging. The modelling of the X-ray tube enables a deeper understanding of the Bremsstrahlung production process in the target as well as the influence of components such as windows, collimators and filters on the spectral and fluence properties of the X-ray beams that are generated. Reference Poludniowski and Evans10,Reference Poludniowski11 Figure 1 shows an example of a simple X-ray tube geometry implemented using the XTUBE component module of the BEAMnrc user code. Reference Rogers, Faddegon, Ding, Ma, We and Mackie12 Information from the manufacturer on the target material (s), thickness (es), angle, electron beam energy and radius and window details can be used to develop the model. Additional collimators, filters and applicators can also be included using other available component modules. X-ray tubes are used for a wide variety of applications, and Monte-Carlo simulation has been applied accordingly. These applications include X-ray tubes in clinical diagnostic CT systems. Reference Bazalova and Verhaegen13 As part of the Monte-Carlo collection of papers in this journal, Aghdam et al used the MCNP code to model the treatment head of an intraoperative electron radiotherapy accelerator in order to calculate the radiation contamination dose in the area around the device. Reference Aghdam, Siavashpour, Aghamiri, Mahdavi and Nafisi14 In another study, the same group investigated the effective SSD dependence on electron energy and applicator size. Reference Aghdam, Baghani, Mahdavi, Aghamiri and Akbari15 Al-Ghorabie used the BEAMnrc code to model the XStrahl 150 kV radiotherapy unit. Simulated X-ray spectra, first and second Half-Value Layers (HVLs) and dose profiles were compared to measured data. Measured and simulated spectra were found to agree to ∼1% and HVLs differed between 2·3 and 3·6%. Percentage depth doses agreed to within 2% and beam profiles in the range 3–5 % depending on applicator size. Reference Al-Ghorabie16 At this point, the reader is reminded that Monte-Carlo simulations are highly sensitive to the configuration parameters used for a particular simulation. For this reason, when seeking to reproduce simulations by others, it is important that the exact same settings are used. An important responsibility therefore falls on the authors of research involving Monte-Carlo simulation to include all relevant configuration parameters to enable reproducibility by others. Reference Sechopoulos, Rogers and Bazalova-Carter17
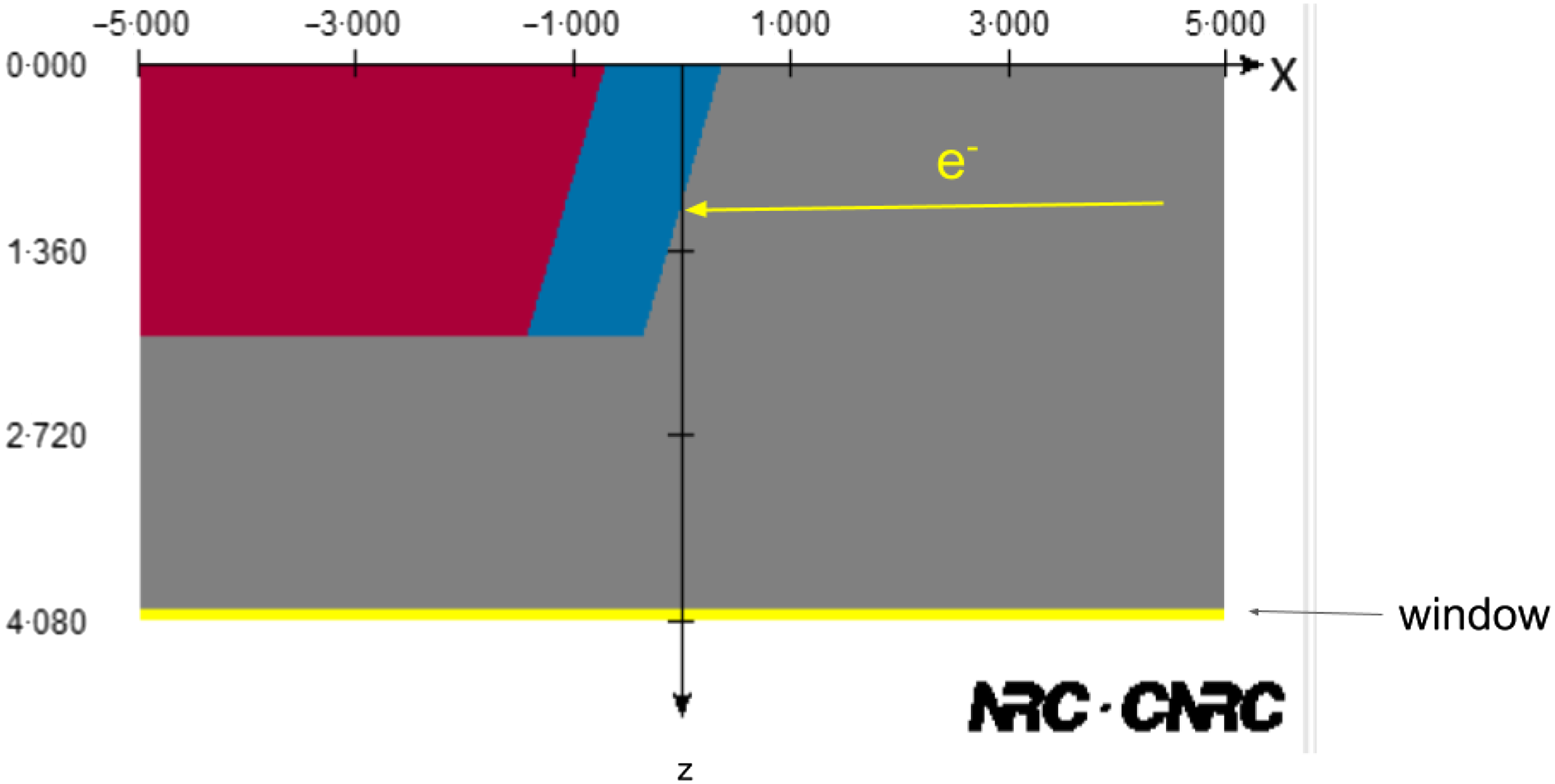
Figure 1. Simple X-ray tube model created using the XTUBE component module of the BEAMnrc user code. Grey indicates a vacuum. Blue indicates the tungsten target embedded on the red copper mounting. Axis dimensions are in centimetres.
Radiotherapy delivery equipment modelling
Monte-Carlo techniques have been widely used to model clinical electron and X-ray beams, patient dosimetry and imaging systems found in the radiotherapy treatment room. Padilla-Cabal et al compared the MCNPX and BEAMnrc Monte-Carlo models for an Elekta Precise SL-25 photon beam. The MC models were compared to measure dosimetry profile data in homogeneous water and homogeneous phantoms containing air, bone and lung equivalent materials. Reference Padilla-Cabal, Pérez-Liva, Lara, Alfonso and Lopez-Pino18 Toossi et al used the MCNPX code to simulate the 8, 12 and 14 MeV electron beams generated by a Siemens Primus linear accelerator. Simulated dosimetry profile data were compared to measured data for different field sizes including applicators as part of a commissioning process. Reference Bahreyni Toossi, Ghorbani, Akbari, Sabet and Mehrpouyan19 Monte-Carlo techniques can also be used to model more specialised radiotherapy equipment such as Tomotherapy Reference Zhao, Mackenzie, Kirkby and Fallone20,Reference Zhao, Mackenzie, Kirkby and Fallone21 and the Cobalt-60 based Gamma Knife. Reference Moskvin, DesRosiers, Papiez, Timmerman, Randall and DesRosiers22–Reference Junios, Irhas and Novitrian24 Mahmoudi et al used the BEAMnrc code to model the beam profiles of the individual and 201 combined beams of the Gamma Knife stereotactic radiotherapy system. Simulated data were compared with measured film dosimetry in a plexiglass head phantom for four different collimator sizes, 4, 8, 14 and 18 mm diameter. Reference Mahmoudi, Shirazi, Geraily, Nia, Bakhshi and Maleki25 It is also worth noting that Monte-Carlo techniques have also been used widely for verifying treatment dosimetry through the use of Electronic Portal Imaging Detector (EPID)-based dosimetry. Reference Kairn, Cassidy, Sandford and Fielding26–Reference Herwiningsih, Hanlon and Fielding29 The technique can offer an accurate calculation of the portal dose response of the detector for comparison to the measured portal dose.
Proton and Heavy Ion beam modelling
Monte-Carlo techniques have been extensively used to model clinical proton and heavy ion beams and their interactions and deposition of dose in patient geometries. Reference Rahman, Bruza, Lin, Gladstone, Pogue and Zhang30–Reference Vedelago, Geser, Muñoz, Stabilini, Yukihara and Jäkel33 Zarifi et al used the GATE code to study the depth dose characteristics of mono-energetic proton pencil beams of energies 5–250 MeV in water and obtain the energy–range relationship. Further, the stopping powers of the proton pencil beams in a water phantom were compared to data from the NIST standard reference database. Reference Zarifi, Ahangari, Jia, Tajik-Mansoury, Najafzadeh and Firouzjaei34 Zafiri et al performed a study to compare the accuracy of the different physics lists (models) that are available in the GATE code when simulating monoenergetic therapeutic proton pencil beams with energies 5–250 MeV. Reference Zarifi, Ahangari, Jia and Tajik-Mansoury35 Chiang et al used TOPAS to model the treatment head of the Mevion HYPERSCAN pencil beam scanning system proton therapy system including the energy modulation system and Adaptive Aperture. Depth doses and in-air spot sizes were found to have good agreement with measured beam data (1 mm and 10 %, respectively). Full-width half maximums and lateral penumbra agreed to within 2 mm. Reference Chiang, Bunker, Jin, Ahmad and Chen36
Imaging system modelling
The GATE Monte-Carlo system, introduced in the companion part I review, has been extensively used to model CT and the emission imaging systems (nuclear medicine, PET and SPECT). The reader is directed to an excellent topical review by Sarrut et al that includes comprehensive lists of the commercially available emission tomography imaging systems that have been modelled and compared against experimental data. Reference Sarrut, Bała and Bardiès37 A number of authors have used Monte-Carlo techniques to model the EPID and cone beam CT imaging systems that are now found on contemporary linear accelerators. This work has included modelling of the X-ray tube and detector systems. A number of authors have modelled a linear accelerator clinical cone beam CT system for the purposes of evaluating patient dosimetry during dosimetry. Reference Downes, Jarvis, Radu, Kawrakow and Spezi38–Reference Spezi, Downes, Radu and Jarvis40 Monte-Carlo has also been used to evaluate and correct for scatter contributions to both megavoltage and kV cone beam CT. Reference Spies, Ebert, Groh, Hesse and Bortfeld41–Reference Swindell and Evans45 Monte-Carlo has been widely used for modelling and optimising MV portal imaging systems for both anatomical imaging and dosimetry. Flampouri et al used the EGSnrc codes to optimise a low atomic number (Z) X-ray Bremsstrahlung target and detector for radiotherapy MV imaging. Reference Flampouri, Evans, Verhaegen, Nahum, Spezi and Partridge46 Accurate modelling of the portal imaging detector response has been performed using Monte-Carlo techniques. The calculated portal dose image can then be compared to a measured image as a method of in-vivo treatment verification. Parent et al developed a Monte-Carlo model for the Elekta iView GT a-Silicon flat panel imager. Reference Parent, Fielding, Dance, Seco and Evans47,Reference Parent, Seco, Evans, Fielding and Dance48 A different technique based on calculation and measurement of radiological thickness was demonstrated by Kairn et al Reference Kairn, Cassidy, Sandford and Fielding26 A number of other authors performed similar studies for Varian liquid ionisation chamber and flat panel imaging detectors Reference Siebers, Kim, Ko, Keall and Mohan28,Reference Spezi and Lewis49
Brachytherapy
While the majority of this overview has focussed on external beam radiotherapy and associated imaging, it is worth noting that Monte-Carlo calculation techniques have been widely used to model the dosimetry of brachytherapy. Many of the Monte-Carlo codes have capabilities for defining the geometries and sources used in brachytherapy, including EGSnrc and its egs_brachy user code, Reference Chamberland, Taylor, Rogers and Thomson50 MCNP Reference Solberg, DeMarco and Chetty51,Reference Zaker, Zehtabian, Sina and Koontz52 and GEANT4· Reference Enger, Landry and D’Amours53–Reference Landry, Reniers, Pignol, Beaulieu and Verhaegen55 For those without GEANT4 experience, brachytherapy simulation capabilities are also offered through the more user-friendly TOPAS and GATE toolkits. Reference Sarrut, Bardiès and Boussion56,Reference Berumen, Ma, Ramos-Méndez, Perl and Beaulieu57 As part of the Monte-Carlo collection in this journal, Dagli et al compared three different dose calculation algorithms for clinical HDR brachytherapy. The aim was to investigate the accuracy of the BrachyDose Monte-Carlo code in heterogeneous media through a comparison with the Eclipse TG-43 dose calculation tool and the Acuros BV model-based algorithm. Acuros BV and BrachyDose were found to have a good agreement, but significant dose differences were seen with the Eclipse TG-43 dose calculation. Reference Dagli, Yurt and Yegin58
Dosimetry and treatment verification
The first step in a Monte-Carlo simulation of a radiotherapy treatment involves modelling the production of the beam of ionising radiation as discussed in Sections 2·1, 2·2 and 2·3. The output from the simulation can then be used as an input to the simulation of the interaction of the beam(s) with a patient, phantom or detector. Computed tomography images of patients and phantoms in DICOM format can be used to accurately create a voxelised model of the geometry or specific anatomy, including the different segmented tissues and structures in a patient. Simulation of MV X-ray and electron beams used in radiotherapy requires the use of a CT-electron density calibration curve that provides the relationship between CT number and electron density for the segmented tissues in the voxelised patient model. As part of this process, it is common to simplify the assignment of electron densities so that the complex tissues existing in the human body are categorised into just a few basic types, e.g. soft tissue, lung, bone, and air.
As part of the Monte-Carlo collection of this journal, Zaman et al used the EGSnrc code to model enhanced dynamic wedge deliveries to heterogeneous slab phantoms containing lung and bone heterogeneities in water-equivalent material. The Monte-Carlo results were compared with calculations using the Anisotropic analytical algorithm (AAA) and the Acuros XB algorithms found in the Varian Eclipse treatment planning system. Reference Zaman, Kakakhel and Hussain59 Yabsantia et al. performed a comparison of 6 MV photon small field output factors measured following the TGS-483 code of practice with calculations performed using the EGSnrc Monte-Carlo code. Measured output factors for three different detectors, the IBA-CC01, Sun Nuclear EDGE and IBA-SFD, were corrected using the TG-483 formalism and compared with the Monte-Carlo simulations performed using the egs_chamber EGSnrc user code. Reference Yabsantia, Suriyapee, Phaisangittisakul, Oonsiri, Sanghangthum and Seuntjens60 Vassiliev et al used the BEAMnrc/DOSXYZnrc Monte-Carlo code to study the effect of motion on target dose coverage for lung stereotactic body radiation therapy patients treated with flattening filter-free beams. Fifteen patient plans were re-calculated using 4D-CT data with and without the flattening filter. The target coverage for treatment planning system calculations was compared with the Monte-Carlo for each of the patients. Reference Vassiliev, Peterson, Chang and Mohan61 Tanha et al investigated the accuracy of a collapsed cone convolution and ETAR algorithm through comparison with a BEAMnrc Monte-Carlo model of the Varian 2100 C/D 18V photon beam. Dosimetric comparisons were made for a pituitary gland treatment planned on a rando-phantom. Differences between the Monte-Carlo and collapsed cone and ETAR were found to be up to 6 and 10 %, respectively. Reference Tanha, Mahdavi and Geraily62 Nithiyanantham et al compared the XVMC Monte-Carlo dose calculation algorithm found in the commercial Monaco treatment planning system to measured doses for small field sizes (8 × 8 up to 40 × 40 mm) in soft tissue equivalent phantoms containing lung and bone heterogeneities. They observed deviations for the smallest field sizes in and around the soft-tissue heterogeneity interfaces. Reference Nithiyanantham, Mani and Raju63 Mamballikalam et al investigated the dosimetry of 6 MV flattening filter-free small fields measured with three different dosimeters, the IBA CC01 pinpoint chamber, the IBA stereotactic field diode and the PTW microDiamond. Measured doses were compared with calculated doses obtained using the PRIMO Monte-Carlo code. The work showed that for field sizes below 1 × 1 cm perturbation and volume averaging corrections should be applied. Reference Mamballikalam, Senthilkumar and Jayadevan64 Chow and Owrangi used the BEAMnrc code to investigate the mucosal dose in the oral and nasal cavity and its dependence on beam energy, beam angle, mucosal thickness and the backscatter from neighbouring bone for small 6 and 18 MV fields generated by a Varian 21 EX accelerator. Reference Chow and Owrangi65 Acar et al compared the accuracy of the Varian Eclipse electron Monte-Carlo dose calculation algorithm with the Gaussian pencil beam algorithm. The work focussed on the ability of both algorithms to calculate peripheral doses for 6 electron beam energies ranging from 6 to 22 MeV. Calculated peripheral doses were compared with measured (ion chamber and EBT film) for three field sizes, 6 × 6, 10 × 10 and 25 × 25 cm. Differences of up to 8·8 % between Gausssian pencil beam and measurements were reduced to less than 4·3 % for electron Monte-Carlo and measurement. Reference Acar, Caglar and Altinok66 Abdul Aziz et al used a BEAMnrc model of a 6 MV photon beam generated by a Siemens Primus linear accelerator to investigate the effect of artefacts due to a titanium hip prosthesis in CT data on the dose distribution in and around the prosthesis. Reference Abdul Aziz, Mohd Kamarulzaman, Mohd Termizi, Abdul Raof and Tajuddin67
Micro/Nano-dosimetry, radio-chemistry and radiobiology
The macroscopic modelling of radiation production and dose deposition Monte-Carlo can also be used to model radiation interactions on the micro and nano-length scale. For these applications, a track structure paradigm, rather than the condensed history technique, is used that models the individual low energy charged particle interactions at the much shorter length scales. GEANT4 has led the way with this through the development of the GEANT4-DNA toolkit, Reference Incerti, Baldacchino and Bernal68,Reference Incerti, Douglass, Penfold, Guatelli and Bezak69 an extension to the GEANT4 toolkit. GEANT4-DNA has been validated for the modelling of the low energy physics interactions in water as well as the production and subsequent interactions of the reactive chemical species following the radiolysis of water. Reference Bernal, Bordage and Brown70,Reference Peukert, Incerti and Kempson71 From a radiobiological perspective, the DNA damage produced by ionising radiation has also been modelled Reference Sakata, Belov and Bordage72 using GEANT4-DNA. Validation of these microscopic track structure simulation codes for different ionising radiations has been performed against laboratory experiments and in comparison with other independent Monte-Carlo codes. Reference Kyriakou, Sakata and Tran73 As has already been indicated, for those without C++ expertise, all these GEANT4-DNA capabilities for low energy physics, chemistry and radiobiology are accessible through the user-friendly TOPAS-nBio toolkit. Reference Schuemann, McNamara and Ramos-Méndez74–Reference Zhu, McNamara and Ramos-Mendez77 Figure 2(a) shows a TOPAS simulation of the simulated tracks of 50 keV electrons traversing a spherical cell model containing mitochondria and gold nanoparticles. Similar models have been used to investigate the nano-scale and radiobiological interactions underpinning dose enhancement with nano-particles and more recently high dose-rate FLASH radiotherapy delivery, Reference Rudek, McNamara, Ramos-Méndez, Byrne, Kuncic and Schuemann78,Reference Ramos-Méndez, Domínguez-Kondo, Schuemann, McNamara, Moreno-Barbosa and Faddegon79 both using TOPAS-nBio. In the Monte-Carlo collection of this journal, Belamri et al used GEANT4 to investigate the potential dose enhancement effect of gold, silver or platinum nano-particles when irradiated with proton beams with energies typical of those used for brain treatments. Reference Belamri, Dib and Belbachir80
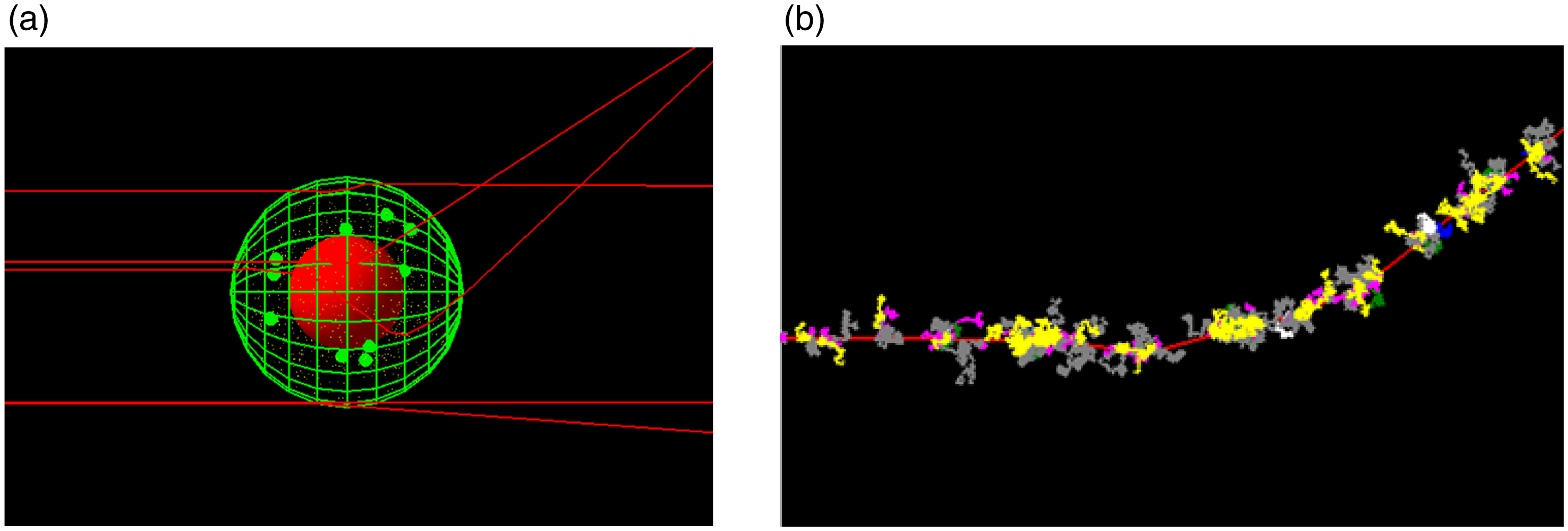
Figure 2. (a) Simple spherical cell model created using TOPAS-nBio. Red central sphere is the nucleus, green spheres are mitochondria and very small yellow spheres are gold nanoparticles. Red lines are the tracks of 50 keV electrons. (b) Free radical chemical species are generated along an electron track (shown in red) as it traverses water.
The TOPAS-nBio code also has the capability to model the chemistry following the physical processes. This includes the free radical chemical species production (e.g. H+ and OH− ions) plus the subsequent diffusion of these species through the cell geometry. Reference Ramos-Méndez, Perl, Schuemann, McNamara, Paganetti and Faddegon75 Figure 2(b) shows an example of the chemical species generated along an electron track as it traverses water. The motion of the chemical species can then be modelled as a function of time.
These radiobiological level simulations of the physics and chemistry of ionising radiation interactions are an extremely powerful tool that can play a crucial role in increasing our understanding of the radiobiology of ionising radiation at the cellular length scale.
Conclusions
Monte-Carlo is a powerful tool for simulating the transport of ionising radiation as it traverses matter. This feature has resulted in the statistical technique being widely and successfully applied to the modelling and simulation of radiotherapy treatments, with most modern radiotherapy treatment planning systems offering a Monte-Carlo algorithm for at least electron beams. A number of different codes are available for free download and require little prior programming experience. These codes enable the user to model the complex geometries in radiotherapy and imaging equipment and the beams they produce. These simulated beams can then be used to accurately model the dosimetry in phantoms, patients, detectors and the radiobiology at smaller micro- and nano-length scales. The Monte-Carlo method has a rich history in the development of new radiation production equipment and detector technology as well as improving our understanding of ionising radiation interactions in human tissues. The continued research into the development of Monte-Carlo codes and algorithms for radiotherapy applications would seem to indicate it will have an increasing role to play well into the foreseeable future.




