No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
The recursively unsolvable halting problem for Turing machines is reduced to the problem of the existence or not of an algorithm for deciding whether a field is finite. The latter problem is further reduced to the decision problem of each of properties

for recursive sets Σ of equations of strong algebraic languages with infinitely many operation symbols.
Decision problems concerning properties of sets of equations were first raised by Tarski [9] and subsequently examined by Perkins [6], McKenzie [4], McNulty [5] and Pigozzi [7]. Perkins is the only one who studied recursive sets; the others investigated finite sets. Since the undecidability of properties Pi for recursive sets of equations does not imply any answer to the corresponding decision problems for finite sets, the latter problems remain open.
The work presented here is part of my Ph.D. thesis [2]. I thank Wilfrid Hodges, who supervised it.
An algebraic language is a first-order language with equality but without relation symbols. It is here denoted by 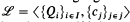 , where Qi is an operation symbol and cj, is a constant symbol.
, where Qi is an operation symbol and cj, is a constant symbol.