Article contents
Expansions of models and turing degrees
Published online by Cambridge University Press: 12 March 2014
Extract
If 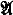 is a countable recursively saturated structure and T is a recursively axiomatizable theory that is consistent with Th(
is a countable recursively saturated structure and T is a recursively axiomatizable theory that is consistent with Th(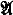 ), then it is well known that
), then it is well known that 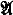 can be expanded to a recursively saturated model of T [7, p. 186]. This is what has made recursively saturated models useful in model theory. Recursive saturation is the weakest notion of saturation for which this expandability result holds. In fact, if
can be expanded to a recursively saturated model of T [7, p. 186]. This is what has made recursively saturated models useful in model theory. Recursive saturation is the weakest notion of saturation for which this expandability result holds. In fact, if 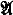 is a countable model of Pr = Th(ω, +), then
is a countable model of Pr = Th(ω, +), then 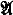 can be expanded to a model of first order Peano arithmetic P just in case
can be expanded to a model of first order Peano arithmetic P just in case 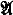 is recursively saturated (see [3]).
is recursively saturated (see [3]).
In this paper we investigate two natural sets of Turing degrees that tell a good deal about the expandability of a given structure. If 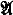 is a recursively saturated structure, I(
is a recursively saturated structure, I(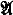 ) consists of the degrees of sets that are recursive in complete types realized in
) consists of the degrees of sets that are recursive in complete types realized in 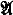 . The second set of degrees, D(
. The second set of degrees, D(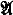 ), consists of the degrees of sets S such that
), consists of the degrees of sets S such that 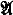 is recursive in S-saturated. In general, I(
is recursive in S-saturated. In general, I(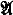 ) ⊆ D(
) ⊆ D(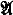 ). Moreover, I(
). Moreover, I(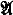 ) is obviously an “ideal” of degrees. For countable structures
) is obviously an “ideal” of degrees. For countable structures 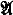 , D(
, D(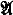 ) is “closed” in the following sense: For any class C ⊆ 2ω, if C is co-r.e. in S for some set S such that
) is “closed” in the following sense: For any class C ⊆ 2ω, if C is co-r.e. in S for some set S such that 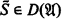 , then there is some σ ∈ C such that
, then there is some σ ∈ C such that  . For uncountable structures
. For uncountable structures 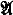 , we do not know whether D(
, we do not know whether D(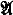 ) must be closed.
) must be closed.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1982
References
REFERENCES
- 9
- Cited by

