Article contents
Forcing for the impredicative theory of classes
Published online by Cambridge University Press: 12 March 2014
Extract
The purpose of this work is to formulate a general theory of forcing with classes and to solve some of the consistency and independence problems for the impredicative theory of classes, that is, the set theory that uses the full schema of class construction, including formulas with quantification over proper classes. This theory is in principle due to A. Morse [9]. The version I am using is based on axioms by A. Tarski and is essentially the same as that presented in [6, pp. 250–281] and [10, pp. 2–11]. For a detailed exposition the reader is referred there. This theory will be referred to as 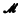 .
.
The reflection principle (see [8]), valid for other forms of set theory, is not provable in 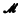 . Some form of the reflection principle is essential for the proofs in the original version of forcing introduced by Cohen [2] and the version introduced by Mostowski [10]. The same seems to be true for the Boolean valued models methods due to Scott and Solovay [12]. The only suitable form of forcing for
. Some form of the reflection principle is essential for the proofs in the original version of forcing introduced by Cohen [2] and the version introduced by Mostowski [10]. The same seems to be true for the Boolean valued models methods due to Scott and Solovay [12]. The only suitable form of forcing for 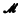 found in the literature is the version that appears in Shoenfield [14]. I believe Vopěnka's methods [15] would also be applicable. The definition of forcing given in the present paper is basically derived from Shoenfield's definition. Shoenfield, however, worked in Zermelo-Fraenkel set theory.
found in the literature is the version that appears in Shoenfield [14]. I believe Vopěnka's methods [15] would also be applicable. The definition of forcing given in the present paper is basically derived from Shoenfield's definition. Shoenfield, however, worked in Zermelo-Fraenkel set theory.
I do not know of any proof of the consistency of the continuum hypothesis with 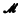 assuming only that
assuming only that 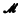 is consistent. However, if one assumes the existence of an inaccessible cardinal, it is easy to extend Gödel's consistency proof [4] of the axiom of constructibility to
is consistent. However, if one assumes the existence of an inaccessible cardinal, it is easy to extend Gödel's consistency proof [4] of the axiom of constructibility to 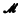 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
References
REFERENCES
- 10
- Cited by

