Article contents
Index sets in Ershov's hierarchy1
Published online by Cambridge University Press: 12 March 2014
Extract
This work is an attempt to characterize the index sets of classes of recursively enumerable sets which are expressible in terms of open sets in the Baire topology on the power set of the set N of natural numbers, usual in recursion theory. Let 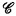 be a class of subsets of N and
be a class of subsets of N and 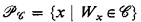 be the set of indices of recursively enumerable sets Wх belonging to
be the set of indices of recursively enumerable sets Wх belonging to 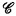 .
.
A well-known theorem of Rice and Myhill (cf. [5, p. 324, Rice-Shapiro Theorem]) states that 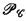 is recursively enumerable if and only if
is recursively enumerable if and only if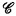 is a r.e. open set. In this case, note that if
is a r.e. open set. In this case, note that if 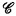 is not empty and does not contain all recursively enumerable sets,
is not empty and does not contain all recursively enumerable sets, 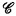 is a
is a 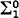 complete set. This theorem will be partially extended to classes which are boolean combinations of open sets by the following:
complete set. This theorem will be partially extended to classes which are boolean combinations of open sets by the following:
(i) There is a canonical boolean combination which represents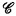 , namely the shortest among boolean combinations which represent
, namely the shortest among boolean combinations which represent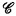 .
.
(ii) The recursive isomorphism type of 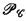 depends on the length n of this canonical boolean combination (and trivial properties of
depends on the length n of this canonical boolean combination (and trivial properties of 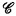 ); for instance,
); for instance, 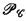 is recursively isomorphic (in the particular case where
is recursively isomorphic (in the particular case where 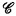 is a boolean combination of recursive open sets) to an elementary set combination Yn or Un, constructed from {х ∣ х Wх) and depending on the length n. We can say also that
is a boolean combination of recursive open sets) to an elementary set combination Yn or Un, constructed from {х ∣ х Wх) and depending on the length n. We can say also that 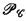 is a complete set in the sense of Ershov's hierarchy [1] (in this particular case).
is a complete set in the sense of Ershov's hierarchy [1] (in this particular case).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
Footnotes
I am grateful to Professor Reznikoff for criticisms and encouragement during the realization of this work.
References
- 7
- Cited by

