Article contents
O-minimal spectra, infinitesimal subgroups and cohomology
Published online by Cambridge University Press: 12 March 2014
Abstract
By recent work on some conjectures of Pillay, each definably compact group G in a saturated o-minimal expansion of an ordered field has a normal “infinitesimal subgroup” G00 such that the quotient G/G00, equipped with the “logic topology”, is a compact (real) Lie group. Our first result is that the functor G ↦ G/G00 sends exact sequences of definably compact groups into exact sequences of Lie groups. We then study the connections between the Lie group G/G00 and the o-minimal spectrum  of G. We prove that G/G00 is a topological quotient of
of G. We prove that G/G00 is a topological quotient of  . We thus obtain a natural homomorphism Ψ* from the cohomology of G/G00 to the (Čech-)cohomology of
. We thus obtain a natural homomorphism Ψ* from the cohomology of G/G00 to the (Čech-)cohomology of  . We show that if G00 satisfies a suitable contractibility conjecture then
. We show that if G00 satisfies a suitable contractibility conjecture then 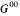 is acyclic in Čech cohomology and Ψ is an isomorphism. Finally we prove the conjecture in some special cases.
is acyclic in Čech cohomology and Ψ is an isomorphism. Finally we prove the conjecture in some special cases.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2007
References
REFERENCES
- 9
- Cited by

