Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Кановей, Владимир Григорьевич
and
Kanovei, Vladimir Grigor'evich
1996.
Топологии, порожденные эффективно суслинскими множествами, и их приложения в дескриптивной теории множеств.
Успехи математических наук,
Vol. 51,
Issue. 3,
p.
17.
Debs, Gabriel
and
Saint Raymond, Jean
2003.
Arbres distingués, bi-arbres et théorèmes de relèvement.
Comptes Rendus. Mathématique,
Vol. 336,
Issue. 8,
p.
625.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2013.
On effective σ‐boundedness and σ‐compactness.
Mathematical Logic Quarterly,
Vol. 59,
Issue. 3,
p.
147.

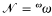 we define a sequence of equivalence relations ‹
we define a sequence of equivalence relations ‹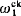 , each
, each 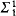 with classes in
with classes in 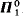
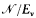 is countable iff
is countable iff 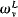 <
< 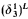 . A new proof is given of a theorem of Hausdorff on partitions of
. A new proof is given of a theorem of Hausdorff on partitions of 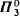 sets.
sets.