Article contents
On a question of G. E. Sacks1
Published online by Cambridge University Press: 12 March 2014
Extract
In [1], Sacks points out that there is one fundamental question: which true statements of ordinary recursion theory remain true when appropriately extended to metarecursion theory?
A particular interest is taken in the question [1]:
Q6. How does one define the jump operator for metarecursion theory? (A satisfactory definition should have the property that if A is metarecursive in B, then the jump of A is metarecursive in the jump of B.)
In [2], Kreisel and Sacks give some definitions of predicates and functions analogous to those of Kleene as follows:
The T-predicate of [2] is analogous to that of Kleene [3]. Its definition is
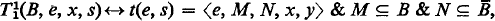
where e is the Gödel number of a finite system of equations E and t(e, s) is a special metarecursive function which indexes “deductions” from E.
U(e, s) is a metarecursive function such that if t(e, s) = 〈e, M, N, x, y〉, then U(e,s) = y.
Two partial functions {e}s and {e} are
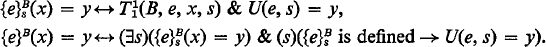
Then e is intrinsically consistent if for all x, s 1 and s 2, if t(e, S 1) = 〈e, M 1N 1, x, y 1〉, t(e, s 2) = 〈e, M 2, N 2, x, y 2〉 and (M 1 ∪ M 2) ∩ (N 1 ∪ N 2) = ∅, then y 1 = y 2.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1970
Footnotes
The author wishes to thank Professor G. E. Sacks for his comments and suggestions regarding the organization and content of this paper.
The referee offered many helpful corrections of the original text. The effects of these suggestions and corrections are through the entire work.
The author wishes to thank the referee, as well.
The main result of this paper was obtained independently by Michael A. Machtey.
References
- 2
- Cited by

