A WEIGHTED 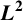$\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR

Abstract

Let H be the Hermite operator 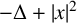$-\Delta +|x|^2$ on 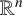$\mathbb {R}^n$. We prove a weighted 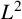$L^2$ estimate of the maximal commutator operator 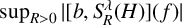$\sup _{R>0}|[b, S_R^\lambda (H)](f)|$, where 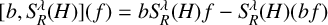$ [b, S_R^\lambda (H)](f) = bS_R^\lambda (H) f - S_R^\lambda (H)(bf) $ is the commutator of a BMO function b and the Bochner–Riesz means 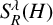$S_R^\lambda (H)$ for the Hermite operator H. As an application, we obtain the almost everywhere convergence of 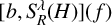$[b, S_R^\lambda (H)](f)$ for large 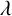$\lambda $ and $f\in L^p(\mathbb {R}^n)$.

1. Introduction

Let H denote the Hermite operator

$$ \begin{align*} -\Delta + |x|^2 =-\sum_{i=1}^n {\partial^2\over \partial x_i^2} + |x|^2, \quad x=(x_1, \ldots, x_n), \quad n\geq 1. \end{align*} $$

The operator H is nonnegative and self-adjoint with respect to the Lebesgue measure on $\mathbb {R}^n$ . The spectrum of the operator H is given by the set $ {2\mathbb N_0} + n$ . Here ${\mathbb N_0}$ denotes the set of nonnegative integers. For each nonnegative integer k, the Hermite polynomials $H_k(t) $ on $\mathbb {R}$ are defined by $H_k(t)=(-1)^k e^{t^2} ({d^k}/{d t^k}) (e^{-t^2})$ , and the Hermite functions $h_k(t):=(2^k k ! \sqrt {\pi })^{-1/2} H_k(t) e^{-t^2/2}$ , $k=0, 1, 2, \ldots $ form an orthonormal basis of $L^2(\mathbb R)$ . For any multiindex $\mu \in {\mathbb N}^n_0$ , the n-dimensional Hermite functions are given by the tensor product of the one-dimensional Hermite functions:

$$ \begin{align*} \Phi_{\mu}(x)=\prod_{i=1}^n h_{\mu_i}(x_i), \quad \mu=(\mu_1, \ldots, \mu_n). \end{align*} $$

Then the functions $\Phi _{\mu }$ are eigenfunctions for the Hermite operator with eigenvalue $(2|\mu |+n)$ and $\{\Phi _{\mu }\}_{\mu \in \mathbb N_0^n}$ forms a complete orthonormal system in $L^2({\mathbb {R}^n})$ . Thus, for every $f\in L^2(\mathbb {R}^n)$ , we have the Hermite expansion

$$ \begin{align*} f(x)=\sum_{\mu\in \mathbb{N}_0^n}\langle f, \Phi_{\mu}\rangle \Phi_\mu(x)=\sum_{k=0}^{\infty}P_kf(x), \end{align*} $$

where $P_k$ denotes the Hermite projection operator given by

$$ \begin{align*} P_kf(x)=\sum_{2|\mu|+n=k}\langle f, \Phi_{\mu}\rangle\Phi_\mu(x). \end{align*} $$

For $R>0$ , the Bochner–Riesz means for H of order $\lambda \geq 0$ are defined by

$$ \begin{align*} S_R^{\lambda}(H)f(x) = \sum_{k=0}^{\infty} \bigg(1-{2k+n\over R^2}\bigg)_+^{\lambda} P_k f(x). \end{align*} $$

The assumption $\lambda \geq 0$ is necessary for $S_R^{\lambda }(H)$ to be defined for all $R>0$ . Note that $S_R^{\lambda }(H)f$ cannot be defined with $R^2=2k+n$ if $\lambda <0$ .

On the space $\mathbb {R}$ , Thangavelu [28] showed that $S_R^\lambda (H)$ is uniformly bounded on $L^p(\mathbb {R})$ for $1\leq p\leq \infty $ provided $\lambda>1/6$ ; if $0<\lambda <1/6$ , the uniform boundedness of $S_R^\lambda (H)$ holds if and only if $4/(6\lambda +3) <p<4/(1-6\lambda )$ . On the space $\mathbb {R}^n$ for dimension $n\geq 2$ , if $\lambda> (n-1)/2$ , Thangavelu [29] showed that $S_R^\lambda (H)$ is uniformly bounded on $L^p(\mathbb {R}^n)$ for $1\leq p\leq \infty $ . Let $n\geq 2,\ 0\leq \lambda \leq (n-1)/2$ and $p\in [1,\infty ]\backslash \, \{2\}$ . It was conjectured (see [30, page 259]) that $S_R^\lambda (H)$ is bounded on $L^p(\mathbb {R}^n)$ uniformly in R if and only if

$$ \begin{align*}\lambda>\lambda(p)=\max\bigg\{n\bigg|\frac1p-\frac12\bigg|-\frac12,0\bigg\}.\end{align*} $$

Thangavelu showed that the $L^p$ boundedness of $S_R^\lambda (H)$ fails if $\lambda <\lambda (p)$ . Karadzhov [19] showed the $L^p$ boundedness of $S_R^\lambda (H)$ by an optimal $L^2$ – $L^p$ spectral projection estimate when p is in the range of $[1,2n/(n+2)]\cup [2n/(n-2),\infty ]$ and ${\lambda>\lambda (p)}$ . Recently, Lee and Ryu [22] invalidated the above conjecture by showing that $\sup _{R>0}\|S_R^\lambda (H)\|_{L^p\rightarrow L^p}\leq C$ only if $\lambda \geq -1/(3p)+n/3(1/2-1/p)>\lambda (p)$ when ${p\in (2(n+1)/n,2(2n-1)/(2n-3))}$ for $n\geq 2$ . Concerning the estimate of the maximal operator, it is known (see [5]) that the maximal operator $\sup _{R>0}|S_R^\lambda (H)f|$ is bounded on $L^p(\mathbb {R}^n)$ for $n\geq 2$ whenever $p\geq 2n/(n-2)$ and $\lambda>\lambda (p)$ . Further, Chen et al. [4] proved that $\sup _{R>0}|S_R^\lambda (H)f|$ is bounded on $L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$ if ${\lambda>\max \{(\alpha -1)/4,0\},}$ which implies the almost everywhere (a.e.) convergence of $S^\lambda _R(H)f$ for all $f\in L^p(\mathbb {R}^n)$ provided that $\lambda>\lambda (p)/2$ with $p\in [2,\infty )$ .

Consider the commutator. Given an operator T and a local integral function b, the commutator of T and b is defined as follows:

$$ \begin{align*}[b,T]f(x):=bTf(x)-T(bf)(x).\end{align*} $$

It is well known that Coifman et al. [9] characterized the boundedness of the commutator $[b,T]$ with Riesz transforms and $b\in \mathrm {BMO}$ . Since then, many investigations have come out of this work: generalizations to spaces of homogeneous type by Uchiyama [32]; multi-parameter extensions by Ferguson and Lacey [12] and by Lacey et al. [20]; in the two-weight setting by Holmes et al. [14]; $L^p$ to $L^q$ boundedness and applications with Jocobian operators by Hytönen [18]; div-curl lemmas by Coifman et al. [8] and by Lacey et al. [21]; additional interpretations in operator theory by Uchiyama [31] and by Nazarov et al. [23]; commutators with classical Bochner–Riesz operators by Álvarez et al. [1] and by Hu and Lu [15, 17].

In [6], the authors of this article and Yan studied the $L^p$ -boundedness of the commutator $[b, S_R^\lambda (H)](f)$ of a BMO function b and the Bochner–Riesz means $S_R^\lambda (H)$ , which are defined by

$$ \begin{align*} [b, S_R^\lambda(H)](f) = bS_R^\lambda(H) f - S_R^\lambda(H)(bf). \end{align*} $$

They showed that if $n\geq 2$ , $1\leq p\leq 2n/(n+2)$ and $\lambda>\lambda (p)$ , then for all $b\in \mathrm {BMO(\mathbb {R}^n)}$ and all $q\in (p,p')$ ,

$$ \begin{align*}\sup_{R>0} \| [b,S_R^{\lambda}(H) ] \|_{q\rightarrow q}\leq C\|b\|_{\mathrm{BMO}}. \end{align*} $$

The purpose of this paper is to follow this line to establish weighted $L^2$ estimates of the commutator of $S_R^\lambda (H)$ and a BMO function b. Our main result is the following theorem.

Theorem 1.1. Let $b\in \mathrm {BMO}(\mathbb {R}^n)$ . For $0\leq \alpha <n$ , if $\lambda>\max \{(\alpha -1)/4,0\}$ , then

$$ \begin{align*} \int_{\mathbb{R}^n} \sup_{R>0}| [b,S^{\lambda}_R(H)]f(x)|^2(1+|x|)^{-\alpha}\,dx\leq C(n,\alpha,\lambda)\|b\|_{\mathrm{BMO}}^2 \int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align*} $$

As a consequence of Theorem 1.1, we have the following result.

Corollary 1.2. Let $2\leq p<\infty $ and $\lambda>\lambda (p)/2.$ Then for any $b\in \mathrm {BMO}(\mathbb {R}^n)$ and $f\in L^p(\mathbb {R}^n)$ ,

$$ \begin{align*}\lim_{R\rightarrow\infty}[b,S^{\lambda}_R(H)]f(x)=0 \end{align*} $$

almost everywhere.

We would like to mention that the classical Bochner–Riesz means on $\mathbb {R}^n$ are defined by

$$ \begin{align*} \widehat{S^{\lambda}_Rf}(\xi) =\bigg(1-{|\xi|^2\over R^2}\bigg)_+^{\lambda} \widehat{f}(\xi) \quad \text{for all }{\xi \in \mathbb{R}^n}. \end{align*} $$

Hu and Lu [16] showed that for $\lambda>0$ , the maximal commutator operator $\sup _{R>0}|[b,S^\lambda _R]f|$ is bounded on $L^2(\mathbb {R}^n)$ . Further, they proved a weighted estimate and showed that the maximal commutator operator $\sup _{R>0}|[b,S^\lambda _R]f|$ is bounded on $L^2(\mathbb {R}^n,|x|^{-\alpha })$ whenever $0<\alpha <n$ and $\lambda>\max \{(\alpha -1)/2,0\}$ in [17].

The proof of Theorem 1.1 relies on a weighted $L^2$ estimate for the square function $ G_{b,\delta }$ , which is defined by

$$ \begin{align*} G_{b,\delta}(f)(x):=\bigg(\int_{0}^{\infty}\bigg|\, \bigg[b,\phi\bigg(\delta^{-1}\bigg( 1- {H\over t^2}\bigg) \bigg) \bigg] f(x)\bigg |^2\frac{dt}{t}\bigg)^{1/2}, \end{align*} $$

where $\phi \in C_c^\infty (\mathbb {R})$ with support $\{x:1/8\leq |x| \leq 1/2\}$ and $|\phi |\leq 1$ (see Proposition 3.1). Indeed, we show that for any $0<\upsilon \leq 1/2$ , there exists a constant $C_{\alpha ,\upsilon }>0$ independent of $\delta $ such that

(1-1) $$ \begin{align} \int_{\mathbb{R}^n}|G_{b,\delta}(f)(x)|^2(1+|x|)^{-\alpha}\,dx\leq C_{\alpha,\upsilon} \|b\|_{\mathrm{BMO}}^2B^{\upsilon}_{\alpha,n}(\delta) \int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx, \end{align} $$

where

(1-2) $$ \begin{align} B^{\upsilon}_{\alpha,n}(\delta)= \begin{cases} \delta^{1-\upsilon} & \mathrm{{if}}\ 0< \alpha< 1, n=1; \alpha=0, n\geq 1;\\[4pt] \delta^{({3-\alpha})/{2}-\upsilon} & \mathrm{{if}}\ 1<\alpha <n, n\geq2. \end{cases} \end{align} $$

To show Inequality (1-1), we use an extension of two nontrivial facts due to [4]. The first is that for any $\alpha \geq 0$ ,

$$ \begin{align*} \|(1+|x|)^{2\alpha}f\|_{L^2(\mathbb{R}^n)}\leq C\|(I+H)^{\alpha}f\|_{L^2(\mathbb{R}^n)} \end{align*} $$

holds for any $f\in {\mathscr S} (\mathbb {R}^n)$ . The second fact is a type of trace lemma for the Hermite operator, that is, for $\alpha>1$ , there exists a constant $C>0$ such that

(1-3) $$ \begin{align} \|\chi_{[k,k+1)}(H)\|_{L^2(\mathbb{R}^n)\rightarrow L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}\leq Ck^{-1/4},\quad k\in \mathbb{N}^+. \end{align} $$

We would like to mention that when $0<\alpha <1$ , Inequality (1-3) is not applicable. To show the square function estimate in Inequality (1-1) for $0<\alpha <1$ , we make use of a weighted Plancherel-type estimate (see Inequality (2-2) and refer to [4, Lemma 2.6] for the proof).

This paper is organized as follows. In Section $2$ , we give some preliminary results about the Hermite operator, and some estimates of the commutator of spectral multipliers and BMO functions, which provide the basic estimates required for the proof of Theorem 1.1. We establish the weighted estimate in Inequality (1-1) of the square function $G_{b,\delta }$ in Section $3$ . The proof of Theorem 1.1 is given in Section $4$ by using the estimate in Inequality (1-1) of the square function $G_{b,\delta }$ . As a consequence of Theorem 1.1, we obtain the proof of Corollary 1.2 at the end of Section $4$ .

2. Preliminary results

We start by recalling some properties of the Hermite operator H. The Hermite operator H satisfies the finite speed propagation property, that is,

(FS) $$ \begin{align} \mathrm{supp}\ K_{\cos(t\sqrt{H})}(x,y)\subseteq \mathfrak{D}_t:=\{(x,y)\in\mathbb{R}^n\times\mathbb{R}^n:|x-y|\leq t\}. \end{align} $$

See for example, [25, Theorem 2]. By Fourier inversion, for any even function F,

$$ \begin{align*}F(\!\sqrt{H})=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\widehat{F}(t)\cos(t\sqrt{H})\,dt.\end{align*} $$

From [7, Lemma I.1], if supp $\, \widehat {F}\subseteq [-t,t]$ , then

$$ \begin{align*} K_{F(\!\sqrt{H})}(x,y)\subseteq \mathfrak{D}_t, \end{align*} $$

which is used in the following.

For any function F with support in $[-1,1]$ and $2\leq p<\infty $ , we define

$$ \begin{align*} \|F\|_{N, _p}:=\bigg(\frac{1}{N}\sum_{i=-N+1}^{N}\sup_{\lambda\in[({i-1})/{N},{i}/{N})}|F(\lambda)|^p\bigg)^{{1}/{p}},\quad N\in \mathbb{N}^+. \end{align*} $$

The following is the trace lemma for the Hermite operator.

Lemma 2.1. For $\alpha>1$ , there exists a constant $C>0$ such that for any $k\in \mathbb {N}^+$ ,

(2-1) $$ \begin{align} \|\chi_{[k,k+1)}(H)\|_{L^2(\mathbb{R}^n)\rightarrow L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}\leq Ck^{-1/4}. \end{align} $$

As a consequence, for any function F supported in $[N/4,N]$ , $N\in \mathbb {N^+}$ and any $\varepsilon>0$ , there exist constants C and $C_\varepsilon $ such that

(2-2) $$ \begin{align} \int_{\mathbb{R}^n}|F(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\leq \begin{cases} CN\|F(N\cdot)\|_{N^2, _2}^2\|f\|_{L^2(\mathbb{R}^n)}^2 & \mbox{{if} } \alpha>1; \\[4pt] C_{\varepsilon}N^{{\alpha}/({1+\varepsilon})}\|F(N\cdot)\|_{N^2,_{2(1+\varepsilon)/\alpha}}^2\|f\|_{L^2(\mathbb{R}^n)}^2 & \mbox{{if} } 0<\alpha\leq1. \end{cases} \end{align} $$

Proof. For the proof of Inequalities (2-1) and (2-2), we refer the reader to [4, Lemmas 1.5, 2.4 and 2.6]. We would like to mention that the estimate in Inequality (2-2) for $\alpha>1$ is equivalent to the estimate in Inequality (2-1). Inequality (2-2) for $0<\alpha \leq 1$ is a consequence of a bilinear interpolation of the estimate in Inequality (2-2) for $\alpha>1$ and the trivial fact $\|F(\!\sqrt {H})f\|_{L^2(\mathbb {R}^n)}=\|F(N\cdot )\|_{L^{\infty }(\mathbb {R})} \|f\|_{L^2(\mathbb {R}^n)}$ .

Lemma 2.2. Let $\alpha \geq 0$ . Then the estimate

$$ \begin{align*} \|(1+|x|)^{\alpha/2}f\|_{L^2(\mathbb{R}^n)}\leq C\|(I+H)^{\alpha/4}f\|_{L^2(\mathbb{R}^n)} \end{align*} $$

holds for all $f\in {\mathscr S}({\mathbb R^n})$ . Here, ${\mathscr S}({\mathbb R^n})$ stands for the class of Schwartz functions in  ${\mathbb R^n}.$

Proof. For the proof, we refer the reader to [4, Lemma 1.4].

Lemma 2.3. Let $b\in \mathrm {BMO}(\mathbb {R}^n)$ . By $M_b$ , we denote the commutator of the Hardy–Littlewood maximal operator defined by

$$ \begin{align*} M_b(f)(x):=\sup_{r>0}r^{-n}\int_{|x-y|<r}|(b(x)-b(y))f(y)|\, dy. \end{align*} $$

If $1<p<\infty $ and $w\in A_p$ , then $M_b$ is bounded on $L^p(\mathbb {R}^n,w)$ with bound $C(n,p)\|b\|_{\mathrm {BMO}}$ .

Proof. For the proof, we refer the reader to [17, Lemma 1] and [13].

Lemma 2.4. Let $M_b(f)$ be defined as above and $\varphi \in C_c^{\infty }({\mathbb {R}})$ . Then for any $\varepsilon>0$ ,

$$ \begin{align*} \sup_{t>0}|[b,\varphi(t^{-2}H)]f(x)|\leq C_{\varepsilon}\|\varphi\|_{W^2_{n+1/2+\varepsilon}} M_b(f)(x). \end{align*} $$

In addition, for any $1<p<\infty $ and $w\in A_p$ ,

$$ \begin{align*} \Big\|\sup_{t>0}|[b,\varphi(t^{-2}H)]f|\,\Big\|_{L^p(\mathbb{R}^n,w)}\leq C_{\varepsilon}\|\varphi\|_{W^2_{n+1/2+\varepsilon}} \|f\|_{L^p(\mathbb{R}^n,w)}. \end{align*} $$

Proof. Let $G(t^{-2}H)=\varphi (t^{-2}H)e^{t^{-2}H}$ , then by the Fourier transform,

$$ \begin{align*}\varphi(t^{-2}H)=\int_{\mathbb{R}} \widehat{G}(\tau) e^{-t^{-2}(1-i\tau)H}\,d\tau,\end{align*} $$

with the kernel

$$ \begin{align*}K_{\varphi(t^{-2}H)}(x,y)=\int_{\mathbb{R}}\widehat{G}(\tau)p_{t^{-2}(1-i\tau)}(x,y)\,d\tau,\end{align*} $$

where $p_{t}(x,y)$ is the heat kernel of the semigroup $e^{-tH}$ . Then,

(2-3) $$ \begin{align} |[b,\varphi(t^{-2}H)]f(x)|&=\bigg|\!\int_{\mathbb{R}^n}K_{\varphi(t^{-2}H)}(x,y)(b(x)-b(y))f(y)\,dy\bigg|\nonumber\\ &\leq \int_{\mathbb{R}}|\widehat{G}(\tau)|\int_{\mathbb{R}^n}|p_{t^{-2}(1-i\tau)}(x,y)(b(x)-b(y))f(y)|\,dy\,d\tau. \end{align} $$

The kernel of $e^{-t^{-2}H}$ has the Gaussian upper bound. Let $z=t^{-2}(1-i\tau )$ . By the Phragmen–Lindelöf theorem, the kernel of $e^{-zH}$ satisfies the following estimate (see [24, Theorem 7.2]):

(2-4) $$ \begin{align} |p_{z}(x,y)|\leq C|z|^{-n/2}(1+|\tau|^2)^{n/4}\exp\bigg(-c\frac{|x-y|^2}{|z|(1+|\tau|^2)^{1/2}}\bigg). \end{align} $$

Let $r=t^{-1}(1+|\tau |^2)^{1/2}$ , $U_0(B)=B(x,r)$ , $U_k(B)=2^{k}B-2^{k-1}B$ for $k\geq 1$ . By Inequality (2-4),

(2-5) $$ \begin{align} \int_{\mathbb{R}^n}|p_{z}(x,y)(b(x)-b(y))f(y)|\,dy &\leq C\sum_{k\geq 0}\frac{\exp(-c2^{2k})}{(1+|\tau|^2)^{-n/2}r^n}\int_{U_k(B)}|b(x)-b(y)||f(y)|\,dy\nonumber \\ &\leq C\sum_{k\geq 0}\frac{2^{kn}\exp(-c2^{2k})}{(1+|\tau|^2)^{-n/2}|2^kB|}\int_{2^{k}B}|b(x)-b(y)||f(y)|\,dy\nonumber \\ &\leq C\sum_{k\geq 0}\frac{2^{kn}\exp(-c2^{2k})}{(1+|\tau|^2)^{-n/2}} M_b(f)(x)\nonumber \\ &\leq C(1+|\tau|^2)^{n/2}M_b(f)(x). \end{align} $$

Note that supp $\varphi \subseteq \mathbb {R}^{+}$ and $\|\varphi \|_{W^2_{n+1/2+\varepsilon }}\approx \|G\|_{W^2_{n+1/2+\varepsilon }} $ . This, in combination with Inequalities (2-3) and (2-5), implies that

(2-6) $$ \begin{align} |[b,\varphi(t^{-2}H)]f(x)|\leq\int_{\mathbb{R}}|\widehat{G}(\tau)|(1+|\tau|^2)^{n/2}M_b(f)(x)\,d\tau\leq C_{\varepsilon}\|\varphi\|_{W^2_{n+1/2+\varepsilon}} M_b(f)(x). \end{align} $$

Finally, the $L^p(\mathbb {R}^n,w)$ of $\sup _{t>0}|[b,\varphi (t^{-2}H)]f|$ follows by Inequality (2-6) and Lemma 2.3.

Lemma 2.5. Let $b\in \mathrm {BMO}(\mathbb {R}^n)$ , $s>n/2$ and let $r_0=\max \{1,n/s\}$ . Then for all Borel functions F such that $\sup _{R>0}\|\eta F(R\cdot )\|_{W_s^{\infty }}<\infty $ where $\eta \in C_c^{\infty }(0,\infty )$ is a fixed function and not identically zero, the commutator $[b,F(\!\sqrt {H})]$ is bounded on $L^p(\mathbb {R}^n,w)$ for all $r_0<p<\infty $ and $w\in A_{p/{r_0}}$ . In addition,

$$ \begin{align*} \|[b,F(\!\sqrt{H})]\|_{L^p(\mathbb{R}^n,w)\rightarrow L^p(\mathbb{R}^n,w)}\leq C\|b\|_{\mathrm{BMO}}\Big(\sup_{R>0}\|\eta F(R\cdot)\|_{W^\infty_s}+|F(0)|\Big). \end{align*} $$

Proof. The Hermite operator has a Gaussian upper bound, and thus it satisfies the condition of [3, Theorem 1.1], which gives this lemma. See also [11, Theorem 3.2].

Lemma 2.6. Let $\varphi \in C_c^{\infty }(\mathbb {R})$ be a nonzero function with support $\{u:1\leq |u|\leq 3\}$ . For $-n<\alpha <n$ ,

(2-7) $$ \begin{align} \int_{\mathbb{R}^n} \sum_{k\in\mathbb{Z}}|\varphi(2^{-k}\!\sqrt{H})f(x)|^2 (1+|x|)^{-\alpha} \,dx\leq C \int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha} \,dx, \end{align} $$

and for any $b\in \mathrm {BMO}(\mathbb {R}^n)$ ,

(2-8) $$ \begin{align} \int_{\mathbb{R}^n} \sum_{k\in\mathbb{Z}}|[b,\varphi(2^{-k}\!\sqrt{H})]f(x)|^2 (1+|x|)^{-\alpha} \,dx\leq C \|b\|_{\mathrm{BMO}}^2\int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha} \,dx. \end{align} $$

Proof. For the proof of Inequality (2-7), we refer to [4, Proposition 2.7]. We show the proof of the estimate in Inequality (2-8) for completeness, although the proof is rather standard. Indeed, let $r_k(t)$ be the Rademacher functions and $\varphi _k(\lambda )=\varphi (2^{-k}\lambda )$ . Define a function

$$ \begin{align*}F(t,\lambda):=\sum_{k\in\mathbb{Z}}r_k(t)\varphi_k(\lambda).\end{align*} $$

By the properties of Rademacher functions,

$$ \begin{align*} \sum_{k\in\mathbb{Z}}|[b,\varphi_k(\!\sqrt{H})]f(x)|^2 &\leq C\int_{0}^{1}\bigg|\sum_{k\in\mathbb{Z}}r_k(t)[b,\varphi_k(\!\sqrt{H})]f(x)\bigg|^2\,dt\\ &=C \int_{0}^{1}|[b,F(t,\!\sqrt{H})]f(x)|^2\,dt. \end{align*} $$

Integrating in x with weight $(1+|x|)^{-\alpha }$ ,

$$ \begin{align*} \int_{\mathbb{R}^n}\sum_{k\in\mathbb{Z}}|[b,\varphi_k(\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha} \,dx\leq C\int_{0}^{1}\int_{\mathbb{R}^n}|[b,F(t,\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha} \,dx\,dt. \end{align*} $$

Let $\eta \in C_c^\infty (\mathbb {R^+})$ . It is easy to obtain that $\sup _{R>0}\|\eta F(t,R\cdot )\|_{W^\infty _{s}(\mathbb {R})}<\infty $ for $s>n/2$ . It follows by Lemma 2.5 and $(1+|x|)^{-\alpha }\in A_2$ whenever $-n<\alpha <n$ that

$$ \begin{align*} &\int_{\mathbb{R}^n}|[b,F(t,\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha} \,dx\\ &\quad\leq C\|b\|^2_{\mathrm{BMO}}\sup_{R>0}\|\eta F(t,R\cdot)\|_{W^\infty_{s}(\mathbb{R})}^2\int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha} \,dx\\ &\quad\leq C\|b\|^2_{\mathrm{BMO}}\int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha} \,dx, \end{align*} $$

with C uniformly in $t\in [0,1]$ .

3. A weighted estimate for the square function

In this section, we show the following weighted $L^2$ estimates for the square function $ G_{b,\delta }$ , which is defined by

$$ \begin{align*} G_{b,\delta}(f)(x):=\bigg(\int_{0}^{\infty}\bigg| \bigg[b,\phi\bigg(\delta^{-1}\bigg( 1- {H\over t^2}\bigg) \bigg) \bigg] f(x)\bigg |^2\frac{dt}{t}\bigg)^{1/2}, \end{align*} $$

where $\phi \in C_c^\infty (\mathbb {R})$ with support $\{x:1/8\leq |x| \leq 1/2\}$ and $|\phi |\leq 1.$

Proposition 3.1. Let $0\leq \alpha <n$ , $0<\delta < 1/2$ . Assume $b\in \mathrm {BMO}(\mathbb {R}^n)$ . Then for any $0<\upsilon \leq 1/2$ , there exists a constant $C_{\alpha ,\upsilon }>0$ independent of $\delta $ such that

$$ \begin{align*} \int_{\mathbb{R}^n}|G_{b,\delta}(f)(x)|^2(1+|x|)^{-\alpha}\,dx\leq C_{\alpha,\upsilon} \|b\|_{\mathrm{BMO}}^2{B^{\upsilon}_{\alpha,n}}(\delta) \int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx, \end{align*} $$

where

$$ \begin{align*} B^{\upsilon}_{\alpha,n}(\delta)= \begin{cases} \delta^{1-\upsilon} & \mbox{{if} } 0< \alpha< 1, n=1; \alpha=0,\ n\geq 1,\\[4pt] \delta^{({3-\alpha})/{2}-\upsilon} & \mbox{{if} } 1<\alpha <n, n\geq2. \end{cases} \end{align*} $$

We select an even function $\eta \in C_c^{\infty }(\mathbb {R})$ supported in $\{u:1/2\leq |u|\leq 2\}$ such that $\sum _{j\in \mathbb {Z}}\eta (2^{-j}u)=1\text { for all }\ u>0.$ Given $0<\delta <1/2$ , let $j_0=[-\log _2\delta ]-1$ . Set $\eta _j(u)=\eta (2^{-j}u)$ for $j>j_0$ and $\eta _{j_0}(u)=1-\sum _{j\geq j_0+1}\eta (2^{-j}u)$ , then we have $\sum _{j\geq j_0}\eta _j (u)\equiv 1 \text {for all } u>0.$ Let us use $\phi _{\delta }(s)$ to denote $\phi (\delta ^{-1}(1-s^2))$ . For $j\geq j_0$ , we define

$$ \begin{align*} \phi_{\delta,j}(s) =\frac{1}{2\pi}\int_{\mathbb{R}}\eta_j(u)\widehat{\phi_{\delta}}(u)e^{isu}\,du. \end{align*} $$

Following from the dyadic decomposition,

(3-1) $$ \begin{align} \phi_{\delta}(t^{-1}s)=\sum_{j\geq j_0}\phi_{\delta,j}(t^{-1}s). \end{align} $$

The following is a useful estimate throughout the paper. For any $N\in \mathbb {N}$ and $j\geq j_0$ ,

(3-2) $$ \begin{align} |\phi_{\delta,j}(s)|\leq \begin{cases} C_N2^{(j_0-j)N} & \mbox{if } |s|\in[1-2\delta,1+2\delta],\\ C_N 2^{j-j_0}(1+2^j|\,s-1|)^{-N} & \mbox{otherwise}. \end{cases} \end{align} $$

See [4, page 23, Equation (3.16)] for the proof.

To prove Proposition 3.1, we need the following lemmas.

Lemma 3.2. Let $0\leq \alpha <n$ , $k\geq 0$ and $j\geq j_0$ . We define an operator associated with $\phi _{\delta ,j}$ by

$$ \begin{align*}T_{j,k}^{\delta}(f):=\bigg(\int_{2^{k-1}}^{2^{k+2}} |\phi_{\delta,j}(t^{-1}\!\sqrt{H})f|^2\frac{dt}{t}\bigg)^{1/2}.\end{align*} $$

Then for any $0<\varepsilon \leq 1/2$ and $N\in \mathbb {N}$ , there exists a constant $C_{\varepsilon ,N}$ such that

$$ \begin{align*} \|T_{j,k}^{\delta}(f)\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}\leq C_{\varepsilon,N}2^{(j_0-j)N}A^{\varepsilon}_{n}(\delta,\alpha)^{1/2}\|f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}, \end{align*} $$

where

(3-3) $$ \begin{align} A^{\varepsilon}_{n}(\delta,\alpha):= \begin{cases} \delta& \mbox{{if} } \alpha=0, n\geq 1,\\ \delta^{1-\varepsilon} & \mbox{{if} } 0<\alpha<1 , n=1,\\ \delta^{({3-\alpha})/{2}} & \mbox{{if} } 1< \alpha<n, n\geq2. \end{cases} \end{align} $$

Lemma 3.3. Let $T_{j,k}^{\delta }$ be defined as in Lemma 3.2 and $k\geq 0$ , $0\leq \alpha < n$ , $j\geq j_0$ . Then for any $0<\varepsilon \leq 1/2$ and $N\in \mathbb {N}$ , there exists a constant $C_{\varepsilon ,N}$ such that

$$ \begin{align*} \|T_{j,k}^{\delta}(f)\|_{L^r(\mathbb{R}^n,(1+|x|)^{-\alpha})} \leq C_{\varepsilon,N}2^{(j_0-j)N}2^{(1-\theta) kn}A^{\varepsilon}_{n}(\delta,\alpha)^{\theta/2}\|f\|_{L^{r'}(\mathbb{R}^n,(1+|x|)^{-\alpha(r'-1)})}, \end{align*} $$

where $\theta =2/r$ , $2< r<\infty $ .

Now, we prove Proposition 3.1 using Lemmas 3.2 and 3.3, whose proofs are given later.

Proof of Proposition 3.1

The facts that the eigenvalue of the Hermite operator is bigger than $1$ and supp $\,\phi \subseteq \{x:1/8\leq |x|\leq 1/2\}$ imply that

$$ \begin{align*} &\int_{0}^{+\infty}\int_{\mathbb{R}^n} |[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{{d}t}{t}\\ &\quad= \int_{1/2}^{+\infty}\int_{\mathbb{R}^n} |[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}. \end{align*} $$

Choose a function $\varphi $ with support $\{s:1\leq |s|\leq 3\}$ and $\sum _{k\in \mathbb {Z}}\varphi (2^{-k}s)=1\text { for all } s\,{>}\,0$ . Let $\varphi _k(s)=\varphi (2^{-k}s)$ . There is a uniform bound C for any $t\in [1/2,\infty )$ such that $\#\{k\in \mathbb {Z}:\phi _{\delta }(t^{-1}s)\varphi _k(s)\neq 0,s>0\}\leq C$ , where $\#$ is the counting measure. Hence,

$$ \begin{align*} &\int_{1/2}^{+\infty}\int_{\mathbb{R}^n} |[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\nonumber\\ &\quad\leq C\sum_{k\in\mathbb{Z}}\int_{1/2}^{\infty}\int_{\mathbb{R}^n}|[b,\phi_{\delta}(t^{-1}\!\sqrt{H})\varphi_k(\!\sqrt{H})]f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}\\ &\quad=C\sum_{k\geq0}\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|[b,\phi_{\delta}(t^{-1}\!\sqrt{H})\varphi_k(\!\sqrt{H})]f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}, \end{align*} $$

where in the last equality, we use the support property of $\phi _{\delta }(t^{-1}s)$ and $\varphi _k(s)$ .

Note that

$$ \begin{align*}[b,\phi_{\delta}(t^{-1}\!\sqrt{H})\varphi_k(\!\sqrt{H})]f= [b,\phi_{\delta}(t^{-1}\!\sqrt{H})]\varphi_k(\!\sqrt{H})f+\phi_{\delta}(t^{-1}\!\sqrt{H})[b,\varphi_k(\!\sqrt{H})]f. \end{align*} $$

It follows that

(3-4) $$ \begin{align} &\int_{0}^{+\infty}\int_{\mathbb{R}^n} |[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\leq C\bigg(\sum_{k\geq0}I_1(k)+\sum_{k\geq0}I_2(k)\bigg), \end{align} $$

where

$$ \begin{align*} I_1(k):=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|\phi_{\delta}(t^{-1}\!\sqrt{H})[b,\varphi_k(\!\sqrt{H})]f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}, \end{align*} $$

$$ \begin{align*} I_2(k):=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]\varphi_k(\!\sqrt{H})f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}. \end{align*} $$

For the first term $I_1(k)$ , it follows by Inequality (3-1) and Minkowski’s inequality that

$$ \begin{align*} I_1(k) &\leq \bigg(\sum_{j\geq j_0}\bigg( \int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |\phi_{\delta,j}(t^{-1}\!\sqrt{H})[b,\varphi_k(\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t} \bigg)^{1/2} \bigg)^2. \end{align*} $$

By Lemma 3.2,

$$ \begin{align*} I_1(k) & \leq C_{\varepsilon,N}\bigg(\sum_{j\geq j_0}2^{(j_0-j)N}\bigg)^2A^{\varepsilon}_{n}(\delta,\alpha) \int_{\mathbb{R}^n}|[b,\varphi_k(\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\\ &\leq C_{\varepsilon}A^{\varepsilon}_{n}(\delta,\alpha) \int_{\mathbb{R}^n}|[b,\varphi_k(\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align*} $$

Then taking the sum over k and using Inequality (2-8) in Lemma 2.6 gives

(3-5) $$ \begin{align} \sum_{k\geq0}I_1(k)\leq C_{\varepsilon}A^{\varepsilon}_{n}(\delta,\alpha) \int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align} $$

For the second term $I_2(k)$ , it follows by Inequality (3-1) and Minkowski’s inequality that

$$ \begin{align*} I_2(k) &\leq \bigg(\sum_{j\geq j_0}\bigg( \int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]\varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t} \bigg)^{1/2} \bigg)^2. \end{align*} $$

We decompose $\mathbb {R}^n$ into disjoint cubes with side length $2^{j-k+2}$ . For a given ${\mathbf {m}=(\mathbf {m}_1,\ldots ,\mathbf {m}_n)\in \mathbb {Z}^n}$ , we define an associated cube by

$$ \begin{align*} Q_{\mathbf{m}}&=[2^{j-k+2}(\mathbf{m}_1-1/2),2^{j-k+2}(\mathbf{m}_1+1/2))\\ &\quad\times\cdots\times[2^{j-k+2}(\mathbf{m}_n-1/2),2^{j-k+2}(\mathbf{m}_n+1/2)). \end{align*} $$

Clearly, $Q_{\mathbf {m}}$ is a cube with centre $2^{j-k+2}(\mathbf {m}_1,\ldots ,\mathbf {m}_n)$ and side length $2^{j-k+2}$ . Here, $\{Q_{\mathbf {m}}\}$ are disjoint and $\mathbb {R}^n=\bigcup _{\mathbf {m}\in \mathbb {Z}^n}Q_{\mathbf {m}}.$ For each $\mathbf {m}\in \mathbb {Z}^n$ , we define $\widetilde {Q}_{\mathbf {m}}$ by

$$ \begin{align*}\widetilde{Q}_{\mathbf{m}} :=\bigcup_{\mathbf{m}'\in \mathbb{Z}^n:\mathrm{dist}(Q_{\mathbf{m}},Q_{\mathbf{m}'})\leq\sqrt{n}2^{j-k+3}}Q_{\mathbf{m}'}.\end{align*} $$

If $t\in [2^{k-1},2^{k+2}]$ , supp $\widehat {\phi _{\delta ,j}(t^{-1}}\cdot )\subseteq [-2^{j-k+2},2^{j-k+2}]$ . By finite speed of propagation in Display (FS), $K_{\phi _{\delta ,j}(t^{-1}\!\sqrt {H})}\subseteq \mathfrak {D}_{2^{j-k+2}}$ . It follows that for any $t\in [2^{k-1},2^{k+2}]$ ,

(3-6) $$ \begin{align} |[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]g| &=\bigg|\sum_{\mathbf{m},\mathbf{m}'\in \mathbb{Z}^n:\mathrm{dist}(Q_{\mathbf{m}},Q_{\mathbf{m}'})\leq \sqrt{n}2^{j-k+3}} \chi_{Q_{\mathbf{m}}}[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]\chi_{Q_{\mathbf{m'}}}g\bigg|\nonumber\\[4pt] &\leq \sum_{\mathbf{m}\in \mathbb{Z}^n} |\kern1.2pt\chi_{Q_{\mathbf{m}}}[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]\chi_{\widetilde{Q}_{\mathbf{m}}}g|, \end{align} $$

where as usual $\chi _{Q_{\mathbf {m}}}$ is the characteristic function of $Q_{\mathbf {m}}$ .

Let $b_{\widetilde {Q}_{\mathbf {m}}}=|\widetilde {Q}_{\mathbf {m}}|^{-1}\int _{\widetilde {Q}_{\mathbf {m}}}b(y)\;dy$ . Obviously,

(3-7) $$ \begin{align} [b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]g =(b-b_{\widetilde{Q}_{\mathbf{m}}})\phi_{\delta,j}(t^{-1}\!\sqrt{H})g-\phi_{\delta,j}(t^{-1}\!\sqrt{H})(b-b_{\widetilde{Q}_{\mathbf{m}}})g. \end{align} $$

It follows from Inequalities (3-6), (3-7) and the disjointness of ${Q}_{\mathbf {m}}$ that

$$ \begin{align*} &\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]\varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\\ &\quad=\sum_{\mathbf{m}\in \mathbb{Z}^n}\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |\chi_{Q_{\mathbf{m}}}[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})] \chi_{\widetilde{Q}_{\mathbf{m}}}\varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\\ &\quad\leq C\sum_{\mathbf{m}\in \mathbb{Z}^n}\Big(E^{1}_{j,k,\mathbf{m}}+E^{2}_{j,k,\mathbf{m}}\Big), \end{align*} $$

where

$$ \begin{align*} E^{1}_{j,k,\mathbf{m}}&:=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |\chi_{Q_{\mathbf{m}}}(b-b_{\widetilde{Q}_{\mathbf{m}}})\phi_{\delta,j}(t^{-1}\!\sqrt{H})\chi_{\widetilde{Q}_{\mathbf{m}}} \varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t},\\ E^{2}_{j,k,\mathbf{m}}&:=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |\chi_{Q_{\mathbf{m}}}\phi_{\delta,j}(t^{-1}\!\sqrt{H})(b-b_{\widetilde{Q}_{\mathbf{m}}})\chi_{\widetilde{Q}_{\mathbf{m}}} \varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}. \end{align*} $$

We select r and q such that $1/2=1/q+1/r$ and $\alpha r/2<n$ so that we can use Lemma 3.3. By Hölder’s inequality,

(3-8) $$ \begin{align} E^{1}_{j,k,\mathbf{m}}&\leq \|b-b_{\widetilde{Q}_{\mathbf{m}}}\|_{L^{q}(\widetilde{Q}_{\mathbf{m}})}^2 \bigg(\!\int_{\mathbb{R}^n}|T_{j,k}^{\delta}(\chi_{\widetilde{Q}_{\mathbf{m}}}\varphi_k(\!\sqrt{H})f)(x)|^r(1+|x|)^{-\alpha r/2}\,dx\bigg)^{2/r}. \end{align} $$

By Lemma 3.3 and Hölder’s inequality again,

$$ \begin{align*} &\bigg(\!\int_{\mathbb{R}^n}|T_{j,k}^{\delta}(\chi_{\widetilde{Q}_{\mathbf{m}}}\varphi_k(\!\sqrt{H})f)(x)|^r(1+|x|)^{-\alpha r/2}\,dx\bigg)^{2/r} \nonumber\\ &\quad \leq {} C_{\varepsilon,N} 2^{2(j_0-j)N} A_n^\varepsilon(\delta,r\alpha/2)^{2/r}2^{2kn(1-2/r)} \bigg(\!\int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{r'}(1+|x|)^{-\alpha r'/2}\,dx\bigg)^{2/{r'}}\nonumber\\ &\quad\leq C_{\varepsilon,N}2^{2(j_0-j)N} A_n^\varepsilon(\delta,r\alpha/2)^{2/r}2^{2kn(1-2/r)} |\widetilde{Q}_{\mathbf{m}}|^{2/q} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align*} $$

By John–Nirenberg’s inequality,

(3-9) $$ \begin{align} \|b-b_{\widetilde{Q}_{\mathbf{m}}}\|_{L^{q}(\widetilde{Q}_{\mathbf{m}})}^2 \leq C_q\|b\|_{\mathrm{BMO}}^2|\widetilde{Q}_{\mathbf{m}}|^{2/q}. \end{align} $$

Recall that $\widetilde {Q}_{\mathbf {m}}$ is contained in a ball with diameter $5\sqrt {n}\cdot 2^{j-k+2}$ and $2^{j_0}\approx \delta ^{-1}$ . In combination with the estimates in Inequalities (3-8)–(3-9) and $2/q=1-2/r$ ,

$$ \begin{align*} E^{1}_{j,k,\mathbf{m}}\leq C_{\varepsilon,r,N}\|b\|_{\mathrm{BMO}}^22^{2(j_0-j)(N-n(1-2/r))} \delta^{-2n(1-2/r)}A_n^\varepsilon(\delta,r\alpha/2)^{2/r} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align*} $$

Similarly, by Hölder’s inequality, Lemma 3.3 and John–Nirenberg’s inequality,

$$ \begin{align*} E^{2}_{j,k,\mathbf{m}}\leq C_{\varepsilon,r,N}\|b\|_{\mathrm{BMO}}^22^{2(j_0-j)(N-n(1-2/r))} \delta^{-2n(1-2/r)}A_n^\varepsilon(\delta,r\alpha/2)^{2/r} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align*} $$

Case 1. $n\geq 2$ and $1<\alpha <n$ .

For any $0<\upsilon \leq 1/2$ and $1<\alpha <n$ , we choose r such that

$$ \begin{align*}2<r<\min\bigg\{\frac{2n}{\alpha},\frac{2(2n+3/2)}{2n+3/2-\upsilon}\bigg\} .\end{align*} $$

See Inequality (3-3) for the definition of $A_n^\varepsilon (\delta ,r\alpha /2)$ . By calculation,

$$ \begin{align*} A_n^\varepsilon(\delta,r\alpha/2)^{2/r}\delta^{-2n(1-2/r)}=\delta^{(3-\alpha)/2-(1-2/r)(2n+3/2)} < \delta^{(3-\alpha)/2-\upsilon}, \end{align*} $$

then there exists a constant $C_1=C_{\alpha ,\upsilon ,N}$ such that

(3-10) $$ \begin{align} E^{1}_{j,k,\mathbf{m}}+E^{2}_{j,k,\mathbf{m}}&\leq C_1\|b\|_{\mathrm{BMO}}^2 2^{2(j_0-j)(N-n(1-2/r))} \delta^{({3-\alpha})/{2}-\upsilon}\int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align} $$

Case 2. $n=1$ and $0<\alpha <1$ .

For any small $0<\varepsilon \leq 1/4$ and $0<\upsilon '\leq 1/4$ , we choose r such that $2<r<\min \{2/\alpha ,2(3-\varepsilon )/(3-\varepsilon -\upsilon ')\}.$ By calculation,

$$ \begin{align*} A_1^\varepsilon(\delta,r\alpha/2)^{2/r}\delta^{-2(1-2/r)}=\delta^{1-\varepsilon-(1-2/r)(3-\varepsilon)} < \delta^{1-\varepsilon-\upsilon'}\leq \delta^{1-\upsilon}, \end{align*} $$

where $0<\upsilon \leq 1/2$ . Then there exists a constant $C_2=C_{\alpha ,\upsilon ,N}$ such that

(3-11) $$ \begin{align} E^{1}_{j,k,\mathbf{m}}+E^{2}_{j,k,\mathbf{m}} &\leq C_2\|b\|_{\mathrm{BMO}}^2 2^{2(j_0-j)(N-n(1-2/r))} \delta^{1-\upsilon} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align} $$

Case 3. $n\geq 1$ and $\alpha =0$ .

For any small $0<\upsilon \leq 1/2$ , we just need to select the r such that $2<r<2 (2n+1)/ (2n+1-\upsilon )$ . Then there exists a constant $C_3=C_{0,\upsilon ,N}$ such that

(3-12) $$ \begin{align} E^{1}_{j,k,\mathbf{m}}+E^{2}_{j,k,\mathbf{m}}\leq C_{3}\|b\|_{\mathrm{BMO}}^2 2^{2(j_0-j)(N-n(1-2/r))} \delta^{1-\upsilon} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}\,dx. \end{align} $$

Next we sum up the terms $E^{1}_{j,k,\mathbf {m}}+E^{2}_{j,k,\mathbf {m}}$ over j and $\mathbf {m}$ . Combining the estimates in Inequalities (3-10), (3-11) and (3-12), choosing N such that $N>n(1-2/r)$ , and using the fact that $\mathbb {R}^n=\bigcup _{\mathbf {m}\in \mathbb {Z}^n}Q_{\mathbf {m}}$ and $\{\widetilde {Q}_{\mathbf {m}}\}$ has finite overlaps, then we obtain that there exists a constant $C_{\alpha ,\upsilon }$ such that

(3-13) $$ \begin{align} I_2(k) &\leq C_4 B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2 \bigg(\sum_{j\geq j_0}\bigg(\sum_{m\in \mathbb{Z}^n} \kern-1.2pt\int_{\widetilde{Q}_m}\!|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx\kern-0.2pt\bigg)^{\kern-1pt 1/2}\kern-0.5pt 2^{(j_0-j)(N-n(1-2/r))} \bigg)^{\kern-1pt2} \nonumber\\ &\leq C_{\alpha,\upsilon}B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2 \int_{\mathbb{R}^n}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx, \end{align} $$

where $B^{\upsilon }_{\alpha ,n}(\delta )$ is defined in Equation (1-2) and $C_4=C_1+C_2+C_3$ .

Finally, summing up the terms $I_2(k)$ over k in the estimate in Inequality (3-13) and using the estimate in Inequality (2-7) in Lemma 2.6,

(3-14) $$ \begin{align} \sum_{k\geq0}I_2(k) &\leq C_{\alpha,\upsilon}B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2 \sum_{k\geq0}\int_{\mathbb{R}^n}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx\nonumber\\ &\leq C_{\alpha,\upsilon}B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2\int_{\mathbb{R}^n}|f(x)|^{2}(1+|x|)^{-\alpha}\,dx, \end{align} $$

where $n=1,0\leq \alpha <1$ ; $n\geq 2, 1< \alpha <n$ or $n\geq 2$ , $\alpha =0$ .

Combining the estimates in Inequalities (3-4), (3-5) and (3-14) and noting $A^{\upsilon }_{n}(\delta ,\alpha )<B^{\upsilon }_{\alpha ,n}(\delta )$ , we obtain that for any $0<\upsilon \leq 1/2$ ,

$$ \begin{align*} \int_{0}^{\infty}\!\!\int_{\mathbb{R}^n}|[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t} \leq C_{\alpha,\upsilon} B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2\!\! \int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align*} $$

Hence, we obtain Proposition 3.1 provided Lemmas 3.2 and 3.3 are proved.

Finally, let us prove Lemmas 3.2 and 3.3.

Proof of Lemma 3.2

We discuss this lemma by distinguishing two cases: $\alpha =0$ and $0<\alpha <n$ .

Case 1. $\alpha =0$ .

Pick a function $\psi \kern1.3pt{\in}\kern1.3pt C_c^{\infty }(\mathbb {R})$ with support $\{s:1\kern1.3pt{\leq}\kern1.3pt |s|\kern1.3pt{\leq}\kern1.3pt 4\}$ such that ${\sum _{\ell \in \mathbb {Z}} \psi (2^{-\ell }s)\kern1.3pt{=}\kern1.3pt1}$ for $ s>0.$ For any $\delta>0$ , let $\psi _{\delta ,\ell }(s)=\psi (2^{-\ell }\delta ^{-1}(1-s))$ for all $\ell \geq 1$ and $\psi _{\delta ,0}(s)=\psi _0(\delta ^{-1}(1-s))$ , where $\psi _0(s)=1-\sum _{\ell \geq 1}\psi (2^{-\ell }s)$ . Then for $k\geq 0$ and $j\geq j_0$ ,

(3-15) $$ \begin{align} &\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})f(x)|^2\,dx\frac{dt}{t}\leq \bigg(\sum_{\ell\geq0}P_{k,j,\ell}(f) ^{1/2}\bigg)^2, \end{align} $$

where

$$ \begin{align*}P_{k,j,\ell}(f)=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})f(x)|^2 \,dx\frac{dt}{t}.\end{align*} $$

Let $i=0,1,\ldots ,i_0=[8\delta ^{-1}]+1$ . $I_i$ is defined by

$$ \begin{align*}I_i=[2^{k-1}+i2^{k-1}\delta,2^{k-1}+(i+1)2^{k-1}\delta].\end{align*} $$

We decompose $[2^{k-1},2^{k+2}]$ into some intervals $\{I_i\}$ with $[2^{k-1},2^{k+2}]\subseteq \bigcup _{i=0}^{i_0}I_i$ . We see that the $\,dt/t$ measure of $I_i$ is less than $\delta $ . We also define a function $\zeta _i$ associated with $I_i$ by

$$ \begin{align*}\zeta_i(s)=\zeta\bigg(i+\frac{2^{k-1}-s}{2^{k-1}\delta}\bigg),\end{align*} $$

where $\zeta \in C_c^{\infty }([-1,1])$ and $\sum _{i\in \mathbb {Z}}\zeta (\cdot -i)=1$ . Since $\psi _{\delta ,\ell }(t^{-1}s)\zeta _{i'}(s)= 0$ for every $t\in I_i$ if $i'\notin [i-2^{\ell +6}, i+2^{\ell +6}]$ , then for any $t\in I_i$ ,

(3-16) $$ \begin{align} |(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})f|^2 &=\bigg|\!\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}}(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\zeta_{i'}(\!\sqrt{H})f\bigg|^2\nonumber\\ &\leq C2^{\ell}\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\zeta_{i'}(\!\sqrt{H})f|^2. \end{align} $$

Then,

(3-17) $$ \begin{align} P_{k,j,\ell}(f)\leq C2^\ell\sum_{i=0}^{i_0}\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}} \int_{I_i}\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\zeta_{i'}(\!\sqrt{H})f(x)|^2\,dx\frac{dt}{t}. \end{align} $$

From the estimate in Inequality (3-2) and supp $\psi _{\delta ,\ell }\subseteq [1-2^{\ell +2}\delta ,1+2^{\ell +2}\delta ], \,\text { for all} \ell \in \mathbb {Z}$ , the function $\phi _{\delta ,j}\psi _{\delta ,\ell }$ satisfies

(3-18) $$ \begin{align} \|(\phi_{\delta,j}\psi_{\delta,\ell})\|_{L^{\infty}(\mathbb{R})}\leq C2^{(j_0-j)N}2^{-\ell N}\quad \mathrm{for}\ \ell\geq0,j\geq j_0, \end{align} $$

which, together with the $L^2$ -boundedness of the spectral multiplier, implies that

(3-19) $$ \begin{align} \|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}&\leq \|\phi_{\delta,j}\psi_{\delta,\ell}\|_{L^{\infty}(\mathbb{R})}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}\nonumber\\ &\leq C_N2^{-\ell N}2^{(j_0-j)N}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}. \end{align} $$

Combining Inequality (3-19) with Inequality (3-17) and using Minkowski’s inequality,

(3-20) $$ \begin{align} \!\!\!\!P_{k,j,\ell}(f) &\leq C_N2^{-(2N-1)\ell}2^{2(j_0-j)N}\sum_{i=0}^{i_0} \sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}}\int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t}\nonumber\\ &= C_N2^{-(2N-1)\ell}2^{2(j_0-j)N}\sum_{i'=-2^{\ell+6}}^{i_0+2^{\ell+6}} \sum_{\{i\in\mathbb{N}\cap[0, i_0]\ :\ |i-i'|\leq2^{\ell+6}\}} \int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t}. \end{align} $$

The decomposition of $[2^{k-2},2^{k+1}]$ into $\{I_i\}_{i=0}^{i_0}$ makes sure that the $\,dt/t$ measure of the interval $I_i$ is uniformly less than $\delta $ . Indeed,

$$ \begin{align*} \int_{2^{k-1}(1+i\delta)}^{2^{k-1}(1+(i+1)\delta)}1\ \frac{dt}{t}=\ln\bigg(1+\frac{\delta}{1+i\delta}\bigg)\leq \ln(1+\delta) \leq \delta. \end{align*} $$

It follows that

(3-21) $$ \begin{align} \sum_{\{i\in\mathbb{N}\cap[0, i_0]\ :\ |i-i'|\leq2^{\ell+6}\}} \int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t} &\leq \delta\sum_{\{i\in\mathbb{N}\cap[0, i_0]\ :\ |i-i'|\leq2^{\ell+6}\}} \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\nonumber\\ &\leq C2^{\ell}\delta \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$

Combining Inequalities (3-20), (3-21) and using the $L^2$ -estimate of the square function for a Hermite operator gives

(3-22) $$ \begin{align} P_{k,j,\ell}(f) &\leq C_N2^{-(2N-2)\ell}2^{2(j_0-j)N}\delta\sum_{i'\in\mathbb{Z}} \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\nonumber\\ &\leq C_N2^{-(2N-2)\ell}2^{2(j_0-j)N}\delta\|f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$

Combining Inequalities (3-15) and (3-22) and summing up the terms $P_{k,j,\ell }(f)$ over $\ell $ gives

$$ \begin{align*} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})f(x)|^2\,dx\frac{dt}{t}\leq C_N2^{2(j_0-j)N}\delta\|f\|_{L^2(\mathbb{R}^n)}^2. \end{align*} $$

Case 2. $0<\alpha <n$ . We discuss the estimate for two cases: $2^{k}\geq 2\delta ^{-1/2}$ and $1\leq 2^{k}<2\delta ^{-1/2}$ .

If $k\geq -\log _2\delta ^{1/2}+1$ , we use [4, Equations (3.38) and (3.39)] with f in place of $\varphi _k(\!\sqrt {H})f$ to obtain

(3-23) $$ \begin{align} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\nonumber\\ &\quad\leq C_N2^{2(j_0-j)N}A^{\varepsilon}_{n}(\delta,\alpha)\int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align} $$

The procedure is still valid if $\varphi _k(\!\sqrt {H})f$ in [4, Equations (3.38) and (3.39)] is replaced by f. This procedure rests on the trace lemma, the weighted Plancherel-type estimate in Inequality (2-2) and the localization strategy that is based on finite speed of propagation. Indeed, Inequality (2-2) gives the bound of spectral multipliers from $L^2(\mathbb {R}^n)$ to $L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$ . To come back to $L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$ , when the physical space is near $\{x\in \mathbb {R}^n:|x|\leq 2^{j-k+2}\}$ , the previous procedure adds the weight $(1+|x|)^{-\alpha }$ into the integral, which would bring a factor $2^{(j-k+1)\alpha }$ for $j>k$ . This factor is advantageous when $2^{k}\geq 2\delta ^{-1/2}$ ; however, it is useless when $1\leq 2^{k}<2\delta ^{-1/2}$ . To overcome this, based on Lemma 2.2, we instead consider the operator: $\int _{2^{k-1}}^{2^{k+2}} |\phi _{\delta ,j}(t^{-1}\!\sqrt {H})(I+H)^{\alpha /4} f(x)|^2\,dt/t$ and estimate its bound from $L^2(\mathbb {R}^n)$ to $L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$ .

If $0\leq k<-\log _2\delta ^{1/2}+1$ , we claim that for any $0<\varepsilon \leq 1/2$ , there exists a constant $C_{\varepsilon ,N}$ such that

(3-24) $$ \begin{align} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4} f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\nonumber\\&\quad\leq C_{\varepsilon,N}2^{2(j_0-j)N}A^{\varepsilon}_{n}(\delta,\alpha)\int_{\mathbb{R}^n}|f(x)|^2\,dx. \end{align} $$

Using Inequality (3-24) and Lemma 2.2,

$$ \begin{align*} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H}) f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\\&\quad\leq C_{\varepsilon,N}2^{2(j_0-j)N}A^{\varepsilon}_{n}(\delta,\alpha)\int_{\mathbb{R}^n}|(I+H)^{-\alpha/4}f(x)|^2\,dx\\ &\quad\leq C_{\varepsilon,N}2^{2(j_0-j)N}A^{\varepsilon}_{n}(\delta,\alpha)\int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx, \end{align*} $$

which in combination with Inequality (3-23) proves Lemma 3.2.

We now turn to verify the claim. Similar to the discussion of Inequality (3-15),

(3-25) $$ \begin{align} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}\leq \bigg(\sum_{\ell\geq0} Q_{j,k,\ell}(f)^{1/2} \bigg)^2, \end{align} $$

where

$$ \begin{align*}Q_{j,k,\ell}(f)=\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}.\end{align*} $$

Arguing as Inequalities (3-16) and (3-17),

$$ \begin{align*} &Q_{j,k,\ell}(f)\\&\quad\leq C2^{\ell}\sum_{i=0}^{i_0}\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}} \int_{I_i}\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4} \zeta_{i'}(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}. \end{align*} $$

The function $\psi _{\delta ,\ell }(t^{-1}s)$ is supported in $[t(1-2^{\ell +2}\delta ),t(1+2^{\ell +2}\delta )]$ . Let $R=1+ [t(1+2^{\ell +2}\delta )]$ . When $n\geq 2$ , using Inequality (2-2) where $1<\alpha <n$ , then

(3-26) $$ \begin{align} &\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}\zeta_{i'}(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\nonumber\\ &\quad\leq R\|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}Rs)(I+|Rs|^2)^{\alpha/4}\|_{R^2,_2}^2\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$

We see that

(3-27) $$ \begin{align} &\|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}Rs)(I+|Rs|^2)^{\alpha/4}\|_{R^2,_2}^2\nonumber\\ &\quad\leq \|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}Rs)(I+|Rs|^2)^{\alpha/4}\|_{L^\infty(\mathbb{R})}^2 \|\chi_{[tR^{-1}(1-2^{\ell+2}\delta),tR^{-1}(1+2^{\ell+2}\delta)]}\|_{R^2,_2}^2. \end{align} $$

From the estimate in Inequality (3-18) and the support property of $\psi _{\delta ,\ell }$ , we know that

(3-28) $$ \begin{align} \|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}Rs)(1+|Rs|^2)^{\alpha/4}\|_{L^\infty(\mathbb{R})}^2\leq C_N2^{-2\ell N}2^{2(j_0-j)N}R^{\alpha}. \end{align} $$

The length of the interval $[tR^{-1}(1-2^{\ell +2}\delta ),tR^{-1}(1+2^{\ell +2}\delta )]$ is $8tR^{-1}2^\ell \delta $ , and thus

$$ \begin{align*}\#\bigg\{i\in \mathbb{Z}:\bigg[\frac{i-1}{R^2},\frac{i}{R^2}\bigg]\cap[tR^{-1}(1-2^{\ell+2}\delta),tR^{-1}(1+2^{\ell+2}\delta)]\neq \emptyset\bigg\}\leq 1+8Rt2^\ell\delta,\end{align*} $$

which implies that

(3-29) $$ \begin{align} \|\chi_{[tR^{-1}(1-2^{\ell+2}\delta),tR^{-1}(1+2^{\ell+2}\delta)]}\|_{R^2,_2}^2 &=\frac{1}{R^2}\sum_{i=-R^2+1}^{R^2}\sup_{s\in[({i-1})/{R^2},{i}/{R^2})} |\chi_{[tR^{-1}(1-2^{\ell+2}\delta),tR^{-1}(1+2^{\ell+2}\delta)]}(s)|^2\nonumber\\ &\leq R^{-2}\min\{R^2,(1+8Rt2^\ell\delta)\}. \end{align} $$

Combining Inequalities (3-27)–(3-29) gives

$$ \begin{align*} \mathrm{{RHS} \ of \ (3\text{-}26)} &\leq C_N2^{-2\ell N}2^{2(j_0-j)N}R^{\alpha-1}\min\{R^2,(1+Rt2^\ell\delta)\}\,\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2. \end{align*} $$

If $2^\ell \delta \leq 1$ , note that $1/2\leq t\approx 2^k\leq C\delta ^{-1/2}$ . It is easy to see that $R\approx t\approx 2^k\leq C\delta ^{-1/2}$ . Then

$$ \begin{align*}R^{\alpha-1}\min\{R^2,(1+Rt2^\ell\delta)\}\leq R^{\alpha-1}(1+R^22^{\ell}\delta) \leq C2^{k(\alpha-1)}(1+2^{\ell+2k}\delta) \leq C2^{\ell}\delta^{(1-\alpha)/2}.\end{align*} $$

If $2^\ell \delta \geq 1$ , note that $1/2\leq t\approx 2^k\leq C\delta ^{-1/2}$ . It is easy to see that $R\leq Ct2^\ell \delta $ . Then

$$ \begin{align*}R^{\alpha-1}\min\{R^2,(1+Rt2^\ell\delta)\}\leq CR^{\alpha+1}\leq C(t2^\ell\delta)^{\alpha+1} \leq C(2^{\ell+k}\delta)^{\alpha+1} \leq 2^{(\alpha+1)\ell}\delta^{(\alpha+1)/2}.\end{align*} $$

Therefore, if $2^k\leq C\delta ^{-1/2}$ ,

(3-30) $$ \begin{align} R^{\alpha-1}\min\{R^2,(1+Rt2^\ell\delta)\}\leq C2^{(\alpha+1)\ell}\delta^{(1-\alpha)/2}. \end{align} $$

As a consequence, for any $N>(\alpha +3)/2$

$$ \begin{align*} \mathrm{{RHS} \ of \ (3\text{-}26)}&\leq C_N2^{-\ell(2N-\alpha-1)}2^{2(j_0-j)N}\delta^{(1-\alpha)/2}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2, \end{align*} $$

which, in combination with the $\,dt/t$ measure of $I_i$ is uniformly less than $\delta $ , Fubini’s theorem and the $L^2$ -estimate of square function for Hermite operators, yields

(3-31) $$ \begin{align} Q_{j,k,\ell}(f)&\leq C_N2^{-\ell(2N-\alpha-2)}2^{2(j_0-j)N} \delta^{(1-\alpha)/2}\sum_{i=0}^{i_0}\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}} \int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t}\nonumber\\ &=C_N2^{-\ell(2N-\alpha-2)}2^{2(j_0-j)N} \delta^{(1-\alpha)/2}\sum_{i'=-2^{\ell+6}}^{i_0+2^{\ell+6}}\sum_{\{i\in\mathbb{N}\cap[0, i_0]\ :\ |i-i'|\leq2^{\ell+6}\}} \int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t}\nonumber\\ &\leq C_N2^{-\ell(2N-\alpha-2)}2^{2(j_0-j)N} \delta^{(1-\alpha)/2}2^{\ell}\delta\sum_{i'\in \mathbb{Z}} \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\nonumber\\ &\leq C_N2^{-\ell(2N-\alpha-3)}2^{2(j_0-j)N} \delta^{(3-\alpha)/2}\|f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$

Putting the estimate in Inequality (3-31) into the estimate in Inequality (3-25) and taking the sum over $\ell $ yields

(3-32) $$ \begin{align} \int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}\leq C_N2^{2(j_0-j)N}\delta^{(3-\alpha)/2}\|f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$

When $n=1$ , this situation can be shown in the same manner as before, the difference is that we use the case where $0<\alpha <1$ in Inequality (2-2). Similar to the discussion of Inequality (3-29),

(3-33) $$ \begin{align} \|\chi_{[tR^{-1}(1-2^{\ell+2}\delta),tR^{-1}(1+2^{\ell+2}\delta)]}\|_{R^2,_{{2(1+\varepsilon)}/{\alpha}}}^2 \leq (R^{-2}\min\{R^2,(1+8Rt2^\ell\delta)\})^{{\alpha}/({1+\varepsilon})}. \end{align} $$

From the estimate in Inequality (2-2) for the case $n=1,\ 0<\alpha <1$ and the estimates in Inequalities (3-28) and (3-33), then for any $\varepsilon>0$ , there exist constants $C_{\varepsilon }$ and $C_{\varepsilon ,N}$ such that

(3-34) $$ \begin{align} &\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}\zeta_{i'}(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\nonumber\\ &\quad\leq C_{\varepsilon} R^{{\alpha}/({1+\varepsilon})}\|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}Rs)(I+|Rs|^2)^{\alpha/4} \|_{R^2,_{{2(1+\varepsilon)}/{\alpha}}}^2\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\nonumber\\ &\quad\leq C_{\varepsilon,N}2^{-2\ell N}2^{2(j_0-j)N} (R^{\varepsilon}\min\{R^2,(1+Rt2^\ell\delta)\})^{{\alpha}/({1+\varepsilon})} \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$

Similarly to the discussion of Inequality (3-30), if $2^k\leq C\delta ^{-1/2}$ ,

(3-35) $$ \begin{align} R^{\varepsilon}\min\{R^2,(1+Rt2^\ell\delta)\}\leq 2^{(2+\varepsilon)\ell}\delta^{-\varepsilon/2}. \end{align} $$

Putting the estimate in Inequality (3-35) into the estimate in Inequality (3-34) yields

$$ \begin{align*} \mathrm{{RHS} \ of \ (3\text{-}34)}&\leq C_{\varepsilon,N}2^{-\ell (2N-\alpha(({2+\varepsilon})/({1+\varepsilon})))}2^{2(j_0-j)N}\delta^{-{\alpha\varepsilon}/{2(1+\varepsilon)}}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\\ &\leq C_{\varepsilon,N}2^{-2\ell (N-\alpha)}2^{2(j_0-j)N}\delta^{-\varepsilon}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2. \end{align*} $$

In the same manner as the estimates in Inequalities (3-31) and (3-32),

$$ \begin{align*}Q_{j,k,\ell}(f)\leq C_{\varepsilon,N}2^{-\ell (2N-2\alpha-2)}2^{2(j_0-j)N}\delta^{1-\varepsilon}\|f\|_{L^2(\mathbb{R}^n)}^2 \end{align*} $$

and

$$ \begin{align*} \int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}\leq C_{\varepsilon,N}2^{2(j_0-j)N}\delta^{1-\varepsilon }\|f\|_{L^2(\mathbb{R}^n)}^2, \end{align*} $$

which in combination with Inequality (3-32) yields Inequality (3-24), so the claim holds. The proof of Lemma 3.2 is complete.

Proof of Lemma 3.3

The proof of the lemma is inspired by [17]. For convenience, we use $\|T\|_{p\to q} $ for the operator norm of T if T is a bounded linear operator from $L^p(\mathbb {R}^n)$ to $L^q(\mathbb {R}^n)$ for given $1\leq p,q\leq \infty $ . We first obtain that $T_{j,k}^{\delta }$ is bounded from $L^1(\mathbb {R}^n)$ to $L^{\infty }(\mathbb {R}^n)$ . To do so, we need to estimate $\|\phi _{\delta ,j}(t^{-1}\!\sqrt {H})\|_{1\rightarrow \infty }$ :

$$ \begin{align*} \|\phi_{\delta,j}(t^{-1}\!\sqrt{H})\|_{1\rightarrow\infty}&\leq \|\phi_{\delta,j}^{1/2}(t^{-1}\!\sqrt{H})\|_{1\rightarrow2}\|\phi_{\delta,j}^{1/2}(t^{-1}\!\sqrt{H})\|_{2\rightarrow\infty}\nonumber\\ &\leq \|\phi_{\delta,j}^{1/2}(t^{-1}\!\sqrt{H})\|^2_{2\rightarrow\infty}\leq\bigg(\sum_{\ell\geq0}\|(\phi_{\delta,j}^{1/2}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\|_{2\rightarrow\infty}\bigg)^2. \end{align*} $$

By [10, Lemma 2.2], supp $\psi _{\delta ,\ell }(t^{-1}s)\subseteq \{s\in \mathbb {R}:|s|\leq (1+2^{\ell +2}\delta )t\}$ and Inequality (3-18),

$$ \begin{align*} \|(\phi_{\delta,j}^{1/2}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\|_{2\rightarrow\infty}&\leq \bigg(\int_{\mathbb{R}^n}|K_{(\phi^{1/2}_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})}(x,y)|^2dy\bigg)^{1/2}\\ &\leq C_Nt^{n/2}2^{-\ell (N-n)/2}2^{(j_0-j)N/2}. \end{align*} $$

Summing the terms $\|(\phi _{\delta ,j}^{\frac 12}\psi _{\delta ,\ell })(t^{-1}\!\sqrt {H})\|_{2\rightarrow \infty }$ over $\ell $ gives that

$$ \begin{align*}\|\phi_{\delta,j}(t^{-1}\!\sqrt{H})\|_{1\rightarrow\infty}\leq C_N t^n2^{(j_0-j)N}.\end{align*} $$

Finally, for any $N\in \mathbb {N}$ and $j\geq j_0$ ,

(3-36) $$ \begin{align} \|T_{j,k}^{\delta}(f)\|_{L^\infty(\mathbb{R}^n)} & \leq \bigg(\int_{2^{k-1}}^{2^{k+2}} ||\phi_{\delta,j}(t^{-1}\!\sqrt{H})f\|_{L^\infty(\mathbb{R}^n)}^2\frac{dt}{t}\bigg)^{1/2} \leq C_N2^{kn}2^{(j_0-j)N}\|f\|_{L^1(\mathbb{R}^n)}. \end{align} $$

Here, $T_{j,k}^{\delta }$ is a sub-linear operator. Using interpolation (see [26, Theorem 2.11] or [2, page 120]) with the estimate in Inequality (3-36) and Lemma 3.2,

$$ \begin{align*} \|T_{j,k}^{\delta}(f)\|_{L^r(\mathbb{R}^n,(1+|x|)^{-\alpha})}\leq C_{\varepsilon,N}2^{(j_0-j)N}2^{(1-\theta) kn}A^{\varepsilon}_{n}(\delta,\alpha)^{\theta/2}\|f\|_{L^{r'}(\mathbb{R}^n,(1+|x|)^{-\alpha(r'-1)})}, \end{align*} $$

where $n\kern1.8pt{=}\kern1.8pt 1,0\kern1.8pt{\leq}\kern1.8pt \alpha \kern1.8pt{<}\kern1.8pt 1$ ; $n\kern1.8pt{\geq}\kern1.8pt 2, 1\kern1.8pt{<}\kern1.8pt \alpha \kern1.8pt{<}\kern1.8ptn$ or $n\kern1.8pt{\geq}\kern1.8pt 2$ , $\alpha \kern1.8pt{=}\kern1.8pt0$ ; $1/r\kern1.8pt{=}\kern1.8pt\theta /2$ and $2\kern1.8pt{<}\kern1.8pt r\kern1.8pt{<}\kern1.8pt \infty $ .

4. Proof of Theorem 1.1

We now begin to prove Theorem 1.1.

Proof. Observe that for any $\lambda>0$ and $\rho <\lambda $ ,

$$ \begin{align*} \bigg(1-\frac{m^2}{R^2}\bigg)^{\lambda}_+ & =\widetilde{C}_{\lambda,\,\rho} R^{-2\lambda}\int_{0}^{R}(R^2-t^2)^{\lambda-\rho-1}t^{2\rho+1}\bigg(1-\frac{m^2}{t^2}\bigg)^\rho_+\,dt. \end{align*} $$

For $\rho <\lambda -1/2$ and $\rho>-1/2$ , we apply the Hölder inequality to obtain

(4-1) $$ \begin{align} |[b,S_R^{\lambda}(H)]f|&=\widetilde{C}_{\lambda,\,\rho}R^{-2\lambda}\bigg|\int_{0}^{R}(R^2-t^2)^{\lambda-\rho-1}t^{2\rho+1} [b,S_t^{\rho}(H)]f\,dt\bigg|\nonumber\\ &\leq C_{\lambda,\,\rho}\bigg(\frac1R\int_{0}^{R}|[b,S_t^{\rho}(H)]f|^2\,dt\bigg)^{1/2}. \end{align} $$

Note that $x_+^{\rho }=\sum _{k\in \mathbb {Z}}2^{-k\rho }\phi (2^kx)$ for some $\phi \in C_c^{\infty } ([1/8,1/2])$ . Let $\phi _k(s)=\phi (2^k(1-s^2))$ , $k\geq 1$ and $\phi _0(s)=\sum _{k\leq 0}2^{-k\rho }\phi (2^k(1-s))$ for $s>0$ . Then,

(4-2) $$ \begin{align} [b,S_t^{\rho}(H)]f=[b,\phi_0(t^{-2}H)]f+\sum_{k\geq1}2^{-k\rho}[b,\phi_k(t^{-1}\!\sqrt{H})]f. \end{align} $$

It follows from Displays (4-1) and (4-2) that

$$ \begin{align*} \sup_{R>0}|[b,S_R^{\lambda}(H)]f| \leq & C_{\lambda,\,\rho}\bigg( \sup_{t>0}|[b,\phi_0(t^{-2}H)]f| +\sum_{k\geq1}2^{-k\rho}\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2\frac{dt}{t}\bigg)^{1/2}\bigg). \end{align*} $$

Note that $\phi _0\in C_c^{\infty }$ with support $\{s:0\leq |s|\leq 1\}$ . By Lemma 2.4, for any $0\leq \alpha <n$ ,

(4-3) $$ \begin{align} \Big\|\sup_{t>0}|[b,\phi_0(t^{-2}H)]f|\ \Big\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})} \leq C\|b\|_{\mathrm{BMO}}\|f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}. \end{align} $$

Let $\rho =\lambda -1/2-\eta $ for some $\eta>0$ . If $\alpha =0$ and $n\in \mathbb {N}^+$ , by Proposition 3.1, for any $0<\upsilon \leq 1/2$ , there exists a constant $C_{0,\upsilon }>0$ such that

(4-4) $$ \begin{align} &\bigg\|\sum_{k\geq1}2^{-k\rho}\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2 \frac{dt}{t}\bigg)^{1/2}\bigg\|_{L^2(\mathbb{R}^n)}\nonumber\\ &\quad\leq \sum_{k\geq1}2^{-k\rho}\bigg\|\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2 \frac{dt}{t}\bigg)^{1/2}\bigg\|_{L^2(\mathbb{R}^n)}\nonumber\\ &\quad\leq C_{0,\upsilon}\|b\|_{\mathrm{BMO}}\sum_{k\geq1}2^{-k(\lambda-\eta-\upsilon)}\|f\|_{L^2(\mathbb{R}^n)}. \end{align} $$

Then the $\mathrm {RHS}$ of Inequality (4-4) is bounded by $C_{0,\upsilon }\|b\|_{\mathrm {BMO}}\|f\|_{L^2(\mathbb {R},(1+|x|)^{-\alpha })}$ provided $\eta ,\upsilon $ are small enough. From the estimates in Inequalities (4-3) and (4-4), we can conclude that $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$ is bounded on $L^2(\mathbb {R}^n)$ for any $n\in \mathbb {N}^+$ .

Similarly, if $n=1$ and $0<\alpha <1$ , by Proposition 3.1, for any $0<\upsilon \leq 1/2$ , there exists a constant $C_{\alpha ,\upsilon }>0$ such that

(4-5) $$ \begin{align} &\bigg\|\sum_{k\geq1}2^{-k\rho}\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2 \frac{dt}{t}\bigg)^{1/2}\bigg\|_{L^2(\mathbb{R},(1+|x|)^{-\alpha})}\nonumber\\ &\quad\leq C_{\alpha,\upsilon}\|b\|_{\mathrm{BMO}}\sum_{k\geq1}2^{-k(\lambda-\eta-\upsilon)}\|f\|_{L^2(\mathbb{R},(1+|x|)^{-\alpha})}. \end{align} $$

Then the $\mathrm {RHS}$ of Inequality (4-5) is bounded by $C_{\alpha ,\upsilon }\|b\|_{\mathrm {BMO}}\|f\|_{L^2(\mathbb {R},(1+|x|)^{-\alpha })}$ provided $\eta ,\upsilon $ are small enough. From the estimates in Inequalities (4-3) and (4-5), we can conclude that $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$ is bounded on $L^2(\mathbb {R},(1+|x|)^{-\alpha })$ for $0< \alpha <1$ .

If $n\geq 2$ and $1<\alpha <n$ , by Proposition 3.1, for any $0<\upsilon \leq 1/2$ , there exists a constant $C_{\alpha ,\upsilon }>0$ such that

(4-6) $$ \begin{align} &\bigg\|\sum_{k\geq1}2^{-k\rho}\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2 \frac{dt}{t}\bigg)^{1/2}\bigg\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}\nonumber\\ &\quad\leq C_{\alpha,\upsilon}\|b\|_{\mathrm{BMO}}\sum_{k\geq1}2^{-k(\lambda-{(\alpha-1)}/{4}-\eta-\upsilon)}\|f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}. \end{align} $$

Then the $\mathrm {RHS}$ of Inequality (4-6) is bounded by $C_{\alpha ,\upsilon }\|b\|_{\mathrm {BMO}}\|f\|_{L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })}$ provided $\eta ,\upsilon $ are small enough. From the estimates in Inequalities (4-3) and (4-6), we can conclude that $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$ is bounded on ${L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })}$ for $1< \alpha <n$ whenever $\lambda>(\alpha -1)/4$ . Combining this with the fact that $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$ is bounded on $L^2(\mathbb {R}^n)$ , we now use the complex interpolation method to obtain that $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$ is bounded on the weighted space ${L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })}$ for $0<\alpha \leq 1$ when $n\geq 2$ . First, we deal with $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$ by Kolmogorov–Seliverstov–Plessner linearization (see [27, page 280]). In fact, we define $\mathcal {K}$ as the nonnegative measurable functions on $\mathbb {R}^n$ that only have a finite number of distinct values. Let $\mathcal {R}(x)\in \mathcal {K}$ . It is claimed that

$$ \begin{align*}\sup_{\mathcal{R}(x)\in\mathcal{K}}\|[b,S_{\mathcal{R}(x)}^{\lambda}(H)]f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}= \|\sup_{R>0}|[b,S_R^{\lambda}(H)]f|\,\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}.\end{align*} $$

It is easy to see that

$$ \begin{align*}|[b,S_{\mathcal{R}(x)}^{\lambda}(H)]f(x)|\leq \sup_{R>0}|[b,S_R^{\lambda}(H)]f(x)|.\end{align*} $$

The converse inequality can be seen from the fact that we can always choose a series of functions $\mathcal {R}_j(x)\in \mathcal {K}$ such that

$$ \begin{align*}\lim_{j\rightarrow+\infty}|[b,S_{\mathcal{R}_j(x)}^{\lambda}(H)]f(x)|= \sup_{R>0}\,|[b,S_R^{\lambda}(H)]f(x)|\quad\text{for all } x\in\mathbb{R}^n.\end{align*} $$

By Lebesgue’s dominated convergence theorem,

$$ \begin{align*} \|\sup_{R>0}|[b,S_R^{\lambda}(H)]f|\ \|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}&= \lim_{j\rightarrow+\infty}\|[b,S_{\mathcal{R}_j(x)}^{\lambda}(H)]f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}\\ &\leq \sup_{\mathcal{R}(x)\in\mathcal{K}}\|[b,S_{\mathcal{R}(x)}^{\lambda}(H)]f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}. \end{align*} $$

Therefore, the boundeness of the sub-linear operator $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$ on $L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$ is equivalent to

$$ \begin{align*}\|[b,S_{\mathcal{R}(x)}^{\lambda}(H)]f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})} \leq C\|f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})},\end{align*} $$

where the constant C is independent of $\mathcal {R}(x)$ . Then the weighted $L^2$ estimate of $[b,S_{\mathcal {R}(x)}^{\lambda }(H)]$ for $0<\alpha \leq 1$ when $\lambda>0$ can be deduced from the complex interpolation theorem (see [26, Theorem 2.11]). As a consequence, we obtain that $\sup _{R>0}|[b,S_R^{\lambda }(H)]|$ is bounded on ${L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })}$ for $0<\alpha \leq 1$ if $\lambda>0$ . The proof of Theorem 1.1 is complete.

Finally, we give a proof of Corollary 1.2.

Proof. For any $f\in C_c^\infty (\mathbb {R}^n)$ and supp $f\subseteq B$ for some ball $B\subseteq \mathbb {R}^n$ , then $(b-b_B)f\in L^2(\mathbb {R}^n)$ and $[b,S^{\lambda }_R(H)]f$ are well defined for any $\lambda>0$ . By the a.e. convergence of the Bochner–Riesz operator $S_R^\lambda (H)$ (see [4, Theorem 1.1]),

$$ \begin{align*}\lim_{R\rightarrow\infty}[b,S^{\lambda}_R(H)]f(x) =\lim_{R\rightarrow\infty}b(x)S^{\lambda}_R(H)(f)(x)-S^{\lambda}_R(H)(bf)(x)=0\quad \text{a.e. } x\in\mathbb{R}^n. \end{align*} $$

Let $0\leq \alpha <n$ . Theorem 1.1 implies the a.e. convergence of $[b,S^{\lambda }_R(H)]f$ for any $f\in L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$ if $\lambda>\max \{(\alpha -1)/4,0\}$ .

For given $p\geq 2$ and $\lambda>\lambda (p)/2$ , we can choose $\alpha $ such that ${n(1-2/p)<\alpha <4\lambda +1}$ and $L^p(\mathbb {R}^n)\subseteq L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$ . Hence, the a.e. convergence of $[b,S^{\lambda }_R(H)]f$ holds for all $f\in L^p(\mathbb {R}^n)$ .