Published online by Cambridge University Press: 09 April 2009
In the terminology of J. R. Isbell [5], an element d of a semigroup S is dominated by a subsemigroup U of S if, for an arbitrary semigroup X and arbitrary homomorphisms α β, from S into X, α(u) = β(u) for every u in U implies α(d) = β(d). The set of elements of S dominated by U is a subsemigroup of S containing U and is called the dominion of U. It was shown by Isbell that if one takes two disjoint isomorphic copies S+, S− of S and forms their amalgamated free product S+ * US− that is to say, the quotient of the free product S+ * S− by the congruence p generated by 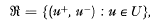 , (u+ and u− being the images of u in S+, S− respectively) then the homomorphisms: μ+: S→ S+ * uS−, μ−: S→ S+ * uS− defined by
, (u+ and u− being the images of u in S+, S− respectively) then the homomorphisms: μ+: S→ S+ * uS−, μ−: S→ S+ * uS− defined by 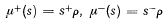 are one-one. Moreover, μ+(s) = μ−(t) only if s = t, and μ+(s)= μ−(s) if and only if s is in the dominion of U. In other words, the two natural copies of S in S+ * uS− intersect precisely in the dominion of U. Thus, in particular, and in the terminology of [3], the amalgam [S+, S−; U] is embeddable if and only if U is self-dominating (that is to say, its own dominion) in S.
are one-one. Moreover, μ+(s) = μ−(t) only if s = t, and μ+(s)= μ−(s) if and only if s is in the dominion of U. In other words, the two natural copies of S in S+ * uS− intersect precisely in the dominion of U. Thus, in particular, and in the terminology of [3], the amalgam [S+, S−; U] is embeddable if and only if U is self-dominating (that is to say, its own dominion) in S.