Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T07:08:08.689Z Has data issue: false hasContentIssue false
  • English
  • Français

INFINITELY MANY SOLUTIONS FOR NONLOCAL SYSTEMS INVOLVING FRACTIONAL LAPLACIAN UNDER NONCOMPACT SETTINGS

Part of: Existence theories Elliptic equations and systems Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  21 December 2018

M. KHIDDI Open the ORCID record for M. KHIDDI [Opens in a new window] ,
S. BENMOULOUD  and
S. M. SBAI
M. KHIDDI*
Affiliation:
E.G.A.L., Département de Mathématiques, Faculté des Sciences, Université Ibn Tofail, BP 133, Kénitra, Morocco email mostapha-2@hotmail.com
S. BENMOULOUD
Affiliation:
E.G.A.L., Département de Mathématiques, Faculté des Sciences, Université Ibn Tofail, BP 133, Kénitra, Morocco
S. M. SBAI
Affiliation:
E.G.A.L., Département de Mathématiques, Faculté des Sciences, Université Ibn Tofail, BP 133, Kénitra, Morocco
*
✉mostapha-2@hotmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study a class of Brezis–Nirenberg problems for nonlocal systems, involving the fractional Laplacian 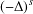$(-\unicode[STIX]{x1D6E5})^{s}$ operator, for 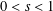$0<s<1$, posed on settings in which Sobolev trace embedding is noncompact. We prove the existence of infinitely many solutions in large dimension, namely when 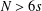$N>6s$, by employing critical point theory and concentration estimates.

Keywords

critical point

MSC classification

Primary: 35J60: Nonlinear elliptic equations
Secondary: 49J35: Minimax problems 35R11: Fractional partial differential equations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 2 , October 2019 , pp. 215 - 233
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Alves, C. O., de Morais Filho, D. C. and Souto, M. A. S., ‘On systems of elliptic equations involving subcritical or critical Sobolev exponents’, Nonlinear Anal. 42(5) (2000), 771–787.Google Scholar
Ambrosetti, A. and Rabinowitz, P. H., ‘Dual variational methods in critical point theory and applications’, J. Funct. Anal. 14(4) (1973), 349–381.Google Scholar
Bahri, A. and Lions, P. L., ‘Morse index of some min–max critical points. I. Application to multiplicity results’, Comm. Pure Appl. Math. 41(8) (1988), 1027–1037.Google Scholar
Barrios, B., Colorado, E., De Pablo, A. and Sánchez, U., ‘On some critical problems for the fractional Laplacian operator’, J. Differential Equations 252(11) (2012), 6133–6162.Google Scholar
Cabré, X. and Tan, J., ‘Positive solutions of nonlinear problems involving the square root of the Laplacian’, Adv. Math. 224(5) (2010), 2052–2093.Google Scholar
Caffarelli, L. and Silvestre, L., ‘An extension problem related to the fractional Laplacian’, Comm. Partial Differential Equations 32(8) (2007), 1245–1260.Google Scholar
Cao, D., Peng, S. and Yan, S., ‘Infinitely many solutions for p-Laplacian equation involving critical Sobolev growth’, J. Funct. Anal. 262(6) (2012), 2861–2902.Google Scholar
Capella, A., Dávila, J., Dupaigne, L. and Sire, Y., ‘Regularity of radial extremal solutions for some non-local semilinear equations’, Comm. Partial Differential Equations 36(8) (2011), 1353–1384.Google Scholar
Cheng, X. and Ma, S., ‘Existence of three nontrivial solutions for elliptic systems with critical exponents and weights’, Nonlinear Anal. 69(10) (2008), 3537–3548.Google Scholar
Devillanova, G. and Solimini, S., ‘Concentration estimates and multiple solutions to elliptic problems at critical growth’, Adv. Differential Equations 7(10) (2002), 1257–1280.Google Scholar
Di Nezza, E., Palatucci, G. and Valdinoci, E., ‘Hitchhiker’s guide to the fractional Sobolev spaces’, Bull. Sci. Math. 136(5) (2012), 521–573.Google Scholar
Ghoussoub, N., Duality and Perturbation Methods in Critical Point Theory, Cambridge Tracts in Mathematics, 107 (Cambridge University Press, Cambridge, 1993).Google Scholar
Ghoussoub, N. and Yuan, C., ‘Multiple solutions for quasi-linear PDEs involving the critical Sobolev and Hardy exponents’, Trans. Amer. Math. Soc. 352(12) (2000), 5703–5743.Google Scholar
He, X., Squassina, M. and Zou, W., ‘The Nehari manifold for fractional systems involving critical nonlinearities’, Preprint, 2015, arXiv:1509.02713.Google Scholar
Lévy-Leblond, J.-M., ‘Electron capture by polar molecules’, Phys. Rev. 153(1) (1967), 1–4.Google Scholar
Liu, Z., ‘On a class of quasilinear elliptic systems with critical growth’, J. Math. Anal. Appl. 403(2) (2013), 558–570.Google Scholar
Liu, Z. and Han, P., ‘Infinitely many solutions for elliptic systems with critical exponents’, J. Math. Anal. Appl. 353(2) (2009), 544–552.Google Scholar
Stinga, P. R. and Torrea, J. L., ‘Extension problem and Harnack’s inequality for some fractional operators’, Comm. Partial Differential Equations 35(11) (2010), 2092–2122.Google Scholar
Struwe, M., ‘A global compactness result for elliptic boundary value problems involving limiting nonlinearities’, Math. Z. 187(4) (1984), 511–517.Google Scholar
Vázquez, J. L., ‘Recent progress in the theory of nonlinear diffusion with fractional Laplacian operators’, Preprint, 2014, arXiv:1401.3640.Google Scholar
Wei, Y. and Su, X., ‘Multiplicity of solutions for non-local elliptic equations driven by the fractional Laplacian’, Calc. Var. Partial Differential Equations 52(1–2) (2015), 95–124.Google Scholar
Willem, M., ‘Mountain pass theorem’, in: Minimax Theorems, Progress in Nonlinear Differential Equations and Applications, 24 (Birkhäuser, Boston, MA, 1996).Google Scholar
Yan, S., Yang, J. and Yu, X., ‘Equations involving fractional Laplacian operator: compactness and application’, J. Funct. Anal. 269(1) (2015), 47–79.Google Scholar