Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T16:11:04.215Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE ACCURACY OF ASYMPTOTIC APPROXIMATIONS TO THE LOG-GAMMA AND RIEMANN–SIEGEL THETA FUNCTIONS

Part of: Elementary classical functions Numerical approximation and computational geometry Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  21 December 2018

RICHARD P. BRENT Open the ORCID record for RICHARD P. BRENT [Opens in a new window]
RICHARD P. BRENT*
Affiliation:
Mathematical Sciences Institute, Australian National University, Canberra, ACT 2600, Australia email richard.brent@anu.edu.au CARMA, University of Newcastle, Callaghan, NSW 2308, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give bounds on the error in the asymptotic approximation of the log-Gamma function 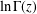$\ln \unicode[STIX]{x1D6E4}(z)$ for complex $z$ in the right half-plane. These improve on earlier bounds by Behnke and Sommer [Theorie der analytischen Funktionen einer komplexen Veränderlichen, 2nd edn (Springer, Berlin, 1962)], Spira [‘Calculation of the Gamma function by Stirling’s formula’, Math. Comp.25 (1971), 317–322], and Hare [‘Computing the principal branch of log-Gamma’, J. Algorithms25 (1997), 221–236]. We show that 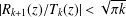$|R_{k+1}(z)/T_{k}(z)|<\sqrt{\unicode[STIX]{x1D70B}k}$ for nonzero $z$ in the right half-plane, where 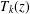$T_{k}(z)$ is the 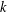$k$th term in the asymptotic series, and 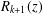$R_{k+1}(z)$ is the error incurred in truncating the series after 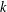$k$ terms. We deduce similar bounds for asymptotic approximation of the Riemann–Siegel theta function 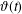$\unicode[STIX]{x1D717}(t)$. We show that the accuracy of a well-known approximation to 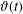$\unicode[STIX]{x1D717}(t)$ can be improved by including an exponentially small term in the approximation. This improves the attainable accuracy for real 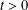$t>0$ from 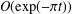$O(\exp (-\unicode[STIX]{x1D70B}t))$ to 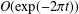$O(\exp (-2\unicode[STIX]{x1D70B}t))$. We discuss a similar example due to Olver [‘Error bounds for asymptotic expansions, with an application to cylinder functions of large argument’, in: Asymptotic Solutions of Differential Equations and Their Applications (ed. C. H. Wilcox) (Wiley, New York, 1964), 16–18], and a connection with the Stokes phenomenon.

Keywords

asymptoticsGamma functionlog-Gamma functionRiemann zeta functionRiemann–Siegel theta function

MSC classification

Primary: 11M06: $zeta (s)$ and $L(s, chi)$
Secondary: 33B15: Gamma, beta and polygamma functions 33B99: None of the above, but in this section 65D20: Computation of special functions, construction of tables
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 3 , December 2019 , pp. 319 - 337
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Abramowitz, M. and Stegun, I. A., Handbook of Mathematical Functions (Dover, New York, 1965).Google Scholar
Askey, R. A. and Roy, R., ‘Gamma function’, NIST Digital Library of Mathematical Functions Ch. 5, http://dlmf.nist.gov/.Google Scholar
Behnke, H. and Sommer, F., Theorie der analytischen Funktionen einer komplexen Veränderlichen, 2nd edn (Springer, Berlin, 1962).Google Scholar
Berry, M. V., ‘The Riemann–Siegel expansion for the zeta function: high orders and remainders’, Proc. R. Soc. Lond. A 450 (1995), 439–462.Google Scholar
Borwein, J. M., Bradley, D. M. and Crandall, R. E., ‘Computational strategies for the Riemann zeta function’, J. Comput. Appl. Math. 121 (2000), 247–296.Google Scholar
Brent, R. P., ‘F. D. Crary & J. B. Rosser, High precision coefficients related to the zeta function [review]’, Math. Comp. 31 (1977), 803–804.Google Scholar
Brent, R. P., ‘On the zeros of the Riemann zeta function in the critical strip’, Math. Comp. 33 (1979), 1361–1372.Google Scholar
Brent, R. P., ‘Asymptotic approximation of central binomial coefficients with rigorous error bounds’, 2016. arXiv:1608.04834v1.Google Scholar
Brent, R. P., van de Lune, J., te Riele, H. J. J. and Winter, D. T., ‘On the zeros of the Riemann zeta function in the critical strip, II’, Math. Comp. 39 (1982), 681–688.Google Scholar
Dilcher, K., ‘Asymptotic behaviour of Bernoulli, Euler, and generalized Bernoulli polynomials’, J. Approx. Theory 49 (1987), 321–330.Google Scholar
Edwards, H. M., Riemann’s Zeta Function (Academic Press, New York, 1974), reprinted by Dover Publications, 2001.Google Scholar
Gabcke, W., ‘Neue Herleitung und explizite Restabschätzung der Riemann–Siegel-Formel’, Dissertation, Mathematisch-Naturwissenschaftlichen, Göttingen, 1979.Google Scholar
Gauss, C. F., ‘Disquisitiones generales circa seriem infinitam …’, Comm. Soc. Reg. Sci. Göttingensis Rec. 2 (1813), reprinted in Carl Friedrich Gauss Werke, Bd. 3, Göttingen, 1876, 123–162.Google Scholar
Gram, J.-P., ‘Note sur les zéros de la fonction 𝜁(s) de Riemann’, Acta Math. 27 (1908), 289–304.Google Scholar
Hare, D. E. G., ‘Computing the principal branch of log-Gamma’, J. Algorithms 25 (1997), 221–236.Google Scholar
Hermite, M. Ch., ‘Sur la fonction log𝛤(a)’, J. reine angew. Math. 115 (1895), 201–208.Google Scholar
Lehmer, D. H., ‘Extended computation of the Riemann zeta function’, Mathematika 3 (1956), 102–108.Google Scholar
Meyer, R. E., ‘A simple explanation of the Stokes phenomenon’, SIAM Rev. 31 (1989), 435–445.Google Scholar
Nemes, G., ‘Generalization of Binet’s Gamma function formulas’, Integral Transforms Spec. Funct. 24 (2013), 597–606.Google Scholar
Olde Daalhuis, A. B., Chapman, S. J., King, J. R., Ockendon, J. R. and Tew, and R. H., ‘Stokes phenomenon and matched asymptotic expansions’, SIAM J. Appl. Math. 55 (1995), 1469–1483.Google Scholar
Olver, F. W. J., ‘Error bounds for asymptotic expansions, with an application to cylinder functions of large argument’, in: Asymptotic Solutions of Differential Equations and Their Applications (ed. Wilcox, C. H.) (Wiley, New York, 1964), 163–183.Google Scholar
Olver, F. W. J., Asymptotics and Special Functions (Academic Press, New York, 1974).Google Scholar
Pólya, G. and Szegö, G., Problems and Theorems in Analysis I, Springer Classics in Mathematics (Springer, Berlin, 1972).Google Scholar
Spira, R., ‘Calculation of the Gamma function by Stirling’s formula’, Math. Comp. 25 (1971), 317–322.Google Scholar
Tweddle, I., ‘Approximating n! , historical origins and error analysis’, Amer. J. Phys. 52 (1984), 487–488.Google Scholar
Watson, G. N., A Treatise on the Theory of Bessel Functions, 2nd edn (Cambridge University Press, Cambridge, 1941).Google Scholar
Whittaker, E. T. and Watson, G. N., A Course of Modern Analysis, 3rd edn (Cambridge University Press, Cambridge, 1920).Google Scholar