Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-13T11:49:16.695Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on Stability Conditions for the Differential Equation x″ + a(t)ƒ(x) = 01

Published online by Cambridge University Press:  09 April 2009

James S. W. Wong
James S. W. Wong
Affiliation:
Mathematics Research Centre University of Wisconsin Madison, Wisconsin, U.S.A. Department of Mathematics Carnegie Mellon University Pittsburgh, Pa., 15213, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the following second order nonlinear differential equation: 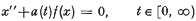where a(t) ∈ C3[0, ∞) and f(x) is a continuous function of x. We are here concerned with establishing sufficient conditions such that all solutions of (1) satisfy (2) 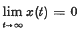Since a(t) is differentiable and f(x) is continuous, it is easy to see that all solutions of (1) are continuable throughout the entire non-negative real axis. 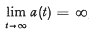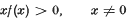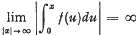It will be assumed throughout that the following conditions hold: 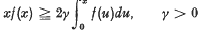Our main results are the following two theorems: Theorem 1. Let 0 < α < 1. If a(t) satisfies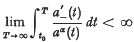where a(t) > 0, t ≧ t0 and 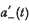= max (−a′(t), 0), and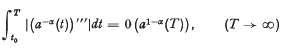then every solution of (1) satisfies (2).

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 9 , Issue 3-4 , May 1969 , pp. 496 - 502
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Chang, K. W., ‘A stability result for the linear differential equation x″ + ƒ(t)x = 0’, J. Australian Math. Soc. 7 (1967), 7–8.CrossRefGoogle Scholar
[2]Lazer, A. C., ‘A stability condition for the differential equation y″ + p(x)y = 0’, Michigan Math. J. 12 (1965), 193–196.CrossRefGoogle Scholar
[3]Meir, A., Willett, D. and Wong, J. S. W., ‘A stability condition for y″ + p(x)y = 0’, Michigan Math. J. 13 (1966), 169–170.Google Scholar