No CrossRef data available.
Published online by Cambridge University Press: 09 April 2009
For a maximal coaction δ of a discrete group G on a C*-algebra A and a normal subgroup N of G, there are at least three natural A × G ×δ| N - A ×δ|1 G/N imprimitivity bimodules: Mansfield's bimodule 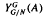 ; the bimodule assembled by Ng from Green's
; the bimodule assembled by Ng from Green's 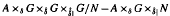 imprimitivity bimodule
imprimitivity bimodule 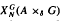 and Katayama duality; and the bimodule assembled from
and Katayama duality; and the bimodule assembled from 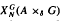 and the crossed-product Mansfield bimodule
and the crossed-product Mansfield bimodule 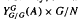 . We show that all three of these are isomorphic, so that the corresponding inducing maps on representations are identical. This can be interpreted as saying that Mansfield and Green induction are inverses of one another ‘modulo Katayama duality’. These results pass to twisted coactions; dual results starting with an action are also given.
. We show that all three of these are isomorphic, so that the corresponding inducing maps on representations are identical. This can be interpreted as saying that Mansfield and Green induction are inverses of one another ‘modulo Katayama duality’. These results pass to twisted coactions; dual results starting with an action are also given.