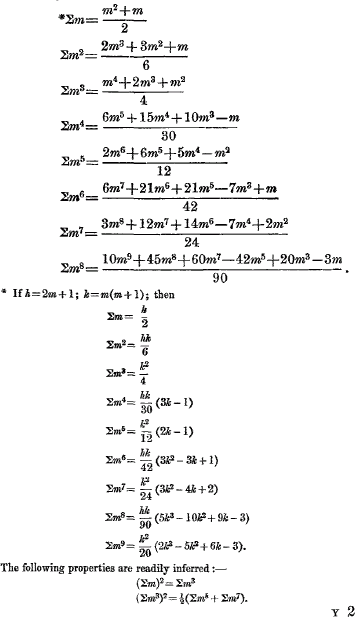No CrossRef data available.
Published online by Cambridge University Press: 18 August 2016
The three heads, into which it has been found expedient to divide the general subject of the present paper, all relate to the consideration of a series of numerical quantities which are supposed to represent, either accurately or approximately, some known or implied law which necessarily has an influence in regulating their progression. Assuming that we only know the values of certain terms of the series of quantities, distributed at stated equidistant intervals, it has been shown that all the intermediate or absent terms are most accurately and expeditiously determined by the process of interpolation, already discussed and practically developed.
page 303 note *

page 309 note * This expression includes only one-half of the extreme values V0, V n . To obtain ΣV'0….n, including all the mn + 1 values, primitive and interpolated, ½(V n + V0) should be added, or the first term of the formula should be replaced by
page 311 note * If for V0, V1, V2, &c., there be substituted their respective numeral coefficients, the formula (6) in either case will express the nth difference of those coefficients, which, being determined by a continuation of the process, must evidently be the central coefficient of the 2nth order of the table. We thus arrive in a most simple manner at the curious summation

page 313 note * An expression equivalent to the first part of this last formula, for finding the area of a figure, was given by the late Thomas Weddle, in the Cambridge and Dublin Mathematical Journal, New Series, vol. ix., p. 79.
page 316 note * For the ratio of the circumference of a circle to its diameter I hare, by means of an empirical process, constructed the concise numerical expression
which is extremely simple considering the degree of accuracy attained. It is correct to no less than ten decimal places of figures.
page 317 note * By successively differentiating the expression (α) referred to, and employing the initial values of the odd differential coefficients, that is, the values when x=0, the formula may be completely resolved into the following remarkable development:—

page 318 note * Here the interval or distance between the given ordinates is supposed to be unity. If the distance be a the curvilinear area will be
page 321 note * In mathematical analysis hyp. log. is always understood, the common logarithm being exclusively employed as a subsidiary in numerical calculations.
page 326 note * The values of log pt are easily got out from a table of log l, by placing a card over log l 0 and another under log lt , so as to obtain their difference without transcribing them; and if for any one of the lives a table of log D is available in place of log l, the factor vt will be thereby included, which will so far abbreviate the calculation. The logarithms taken to five places will be quite sufficient.
page 327 note * In official practice it is a safe and convenient rule to take the yearly premium a year higher when it is to be paid quarterly, and half a year higher when it is to be paid halfyearly. This will rather more than cover the true calculation, as it should do to provide for the cost of additional receipts, &c.
page 329 note * A further extension of this formula will show a remarkable approximation of the terms to a geometrical series.
page 303 note *