Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T16:36:49.275Z Has data issue: false hasContentIssue false
  • English
  • Français

CHABAUTY LIMITS OF ALGEBRAIC GROUPS ACTING ON TREES THE QUASI-SPLIT CASE

Part of: Linear algebraic groups and related topics Structure and classification of infinite or finite groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  06 August 2018

Thierry Stulemeijer
Thierry Stulemeijer*
Affiliation:
Max Planck Institute for Mathematics, Vivatsgasse 7, 53111 Bonn, Germany (tstulemeijer@mpim-bonn.mpg.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a locally finite leafless tree $T$, various algebraic groups over local fields might appear as closed subgroups of 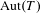$\operatorname{Aut}(T)$. We show that the set of closed cocompact subgroups of 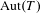$\operatorname{Aut}(T)$ that are isomorphic to a quasi-split simple algebraic group is a closed subset of the Chabauty space of 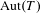$\operatorname{Aut}(T)$. This is done via a study of the integral Bruhat–Tits model of 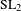$\operatorname{SL}_{2}$ and 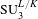$\operatorname{SU}_{3}^{L/K}$, that we carry on over arbitrary local fields, without any restriction on the (residue) characteristic. In particular, we show that in residue characteristic $2$, the Tits index of simple algebraic subgroups of 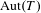$\operatorname{Aut}(T)$ is not always preserved under Chabauty limits.

Keywords

group theory and generalizationstopological groupslinear algebraic groups

MSC classification

Primary: 20E08: Groups acting on trees 20E42: Groups with a $BN$-pair; buildings 20F65: Geometric group theory 20G25: Linear algebraic groups over local fields and their integers
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 4 , July 2020 , pp. 1031 - 1091
Check for updates
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Postdoctoral fellow at the Max Planck Institute for Mathematics in Bonn.

References

Abramenko, P. and Nebe, G., Lattice chain models for affine buildings of classical type, Math. Ann. 322(3) (2002), 537–562.Google Scholar
Borel, A. and Tits, J., Homomorphismes ‘abstraits’ de groupes algébriques simples, Ann. of Math. (2) 97 (1973), 499–571 (French).10.2307/1970833Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron Models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), Volume 21 (Springer, Berlin, 1990).Google Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local, Publ. Math. Inst. Hautes Études Sci. 41 (1972), 5–251 (French).Google Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local. II. Schémas en groupes, in Existence d’une donnée radicielle valuée, Publications Mathématiques. Institut de Hautes Études Scientifiques, Volume 60, pp. 197–376. (1984) (French).Google Scholar
Bruhat, F. and Tits, J., Schémas en groupes et immeubles des groupes classiques sur un corps local, Bull. Soc. Math. France 112(2) (1984), 259–301 (French).Google Scholar
Bruhat, F. and Tits, J., Schémas en groupes et immeubles des groupes classiques sur un corps local. II. Groupes unitaires, Bull. Soc. Math. France 115(2) (1987), 141–195 (French, with English summary).10.24033/bsmf.2073Google Scholar
Burger, M. and Mozes, S., CAT(-1)-spaces, divergence groups and their commensurators, J. Amer. Math. Soc. 9(1) (1996), 57–93.Google Scholar
Caprace, P.-E. and Radu, N., Chabauty limits of simple groups acting on trees, preprint, 2016, arXiv:1608.00461.Google Scholar
Caprace, P.-E. and Stulemeijer, T., Totally disconnected locally compact groups with a linear open subgroup, Int. Math. Res. Not. IMRN 24 (2015), 13800–13829.Google Scholar
Conrad, B., Gabber, O. and Prasad, G., Pseudo-reductive Groups, in New Mathematical Monographs, second edition, Volume 26 (Cambridge University Press, Cambridge, 2015).Google Scholar
Deligne, P., Les corps locaux de caractéristique p, limites de corps locaux de caractéristique 0, Representations of reductive groups over a local field, pp. 119–157 (Travaux en Cours, Hermann, Paris, 1984) (French).Google Scholar
Demazure, M. and Gabriel, P., Groupes algébriques. Tome I: Géométrie algébrique, généralités, groupes commutatifs, Masson & Cie, Éditeur, Paris; North-Holland Publishing Co., Amsterdam, Avec un appendice Corps de classes local par Michiel Hazewinkel, 1970 (French).Google Scholar
Fesenko, I. B. and Vostokov, S. V., Local Fields and Their Extensions, second edition, Translations of Mathematical Monographs, Volume 121 (American Mathematical Society, Providence, RI, 2002). With a foreword by Igor R. Shafarevich.Google Scholar
Georges, E., surjective map of rings with same dimension, Mathematics Stack Exchange. URL: http://math.stackexchange.com/q/604091 (version: 2013-12-12).Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV, Publ. Math. Inst. Hautes Études Sci. 32 (1967), 361 (French).Google Scholar
Kazhdan, D., Representations of groups over close local fields, J. Anal. Math. 47 (1986), 175–179.Google Scholar
Knus, M.-A., Merkurjev, A., Rost, M. and Tignol, J.-P., The Book of Involutions, American Mathematical Society Colloquium Publications, Volume 44 (American Mathematical Society, Providence, RI, 1998). With a preface in French by J. Tits.Google Scholar
Lang, S., Algebraic number Theory, in Graduate Texts in Mathematics, second edition, Volume 110 (Springer, New York, 1994).Google Scholar
Mazurkiewicz, S. and Sierpiński, W., Contribution à la topologie des ensembles dénombrables, Fund. Math. 1(1) (1920), 17–27 (fre).Google Scholar
Pierce, R. S., Associative Algebras, Graduate Texts in Mathematics, Volume 88 (Springer, New York, 1982). Studies in the History of Modern Science, 9.Google Scholar
Pink, R., Compact subgroups of linear algebraic groups, J. Algebra 206(2) (1998), 438–504.Google Scholar
Radu, N., A classification theorem for boundary 2-transitive automorphism groups of trees, Invent. Math. 209(1) (2017), 1–60.Google Scholar
De La Salle, M. and Tessera, R., Local-to-global rigidity of Bruhat-Tits buildings, Illinois J. Math. 60(3–4) (2016), 641–654.Google Scholar
Serre, J.-P., Local Fields, Graduate Texts in Mathematics, Volume 67 (Springer, New York, 1979). Translated from the French by Marvin Jay Greenberg.10.1007/978-1-4757-5673-9Google Scholar
The Stacks Project Authors, Stacks Project, 2016. URL: http://stacks.math.columbia.edu.Google Scholar
Stulemeijer, T., Reference for Hensel’s Lemma in Algebraic Geometry, URL:http://mathoverflow.net/q/234709 (version: 2016-03-28).Google Scholar
Tits, J., Classification of algebraic semisimple groups, in Algebraic Groups and Discontinuous Subgroups, Proceedings of Symposia in Pure Mathematics, Boulder, CO, pp. 33–62 (American Mathematical Society, Providence, RI, 1966).Google Scholar
Tits, J., Buildings of Spherical Type and Finite BN-pairs, Lecture Notes in Mathematics, Volume 386 (Springer, New York, 1974).Google Scholar
Tits, J., Reductive groups over local fields, in Automorphic Forms, Representations and L-functions, Proceedings of Symposia in Pure Mathematics, Oregon State Univ., Corvallis, OR, 1977, Volume XXXIII, pp. 29–69 (American Mathematical Society, Providence, RI, 1979).Google Scholar
Tits, J., Immeubles de type affine, in Buildings and the Geometry of Diagrams (Como, (1984), Lecture Notes in Mathematics, Volume 1181, pp. 159–190 (Springer, Berlin, 1986) (French).Google Scholar
Weiss, R. M., The Structure of Affine Buildings, Annals of Mathematics Studies, Volume 168 (Princeton University Press, Princeton, NJ, 2009).Google Scholar