1 Introduction
This article represents our attempt to improve the previous results on defining and understanding overconvergent Eichler–Shimura maps in [Reference Andreatta, Iovita and Stevens5] and [Reference Andreatta, Iovita and Stevens6].
We fix a prime integer
![]() $p>2$
. We recall that an (overconvergent) Eichler–Shimura morphism is a comparison map describing weight k overconvergent modular symbols, seen as pro-Kummer étale cohomology classes of a sheaf of weight k distributions
$p>2$
. We recall that an (overconvergent) Eichler–Shimura morphism is a comparison map describing weight k overconvergent modular symbols, seen as pro-Kummer étale cohomology classes of a sheaf of weight k distributions
![]() ${\mathbb D}_k$
(where
${\mathbb D}_k$
(where
![]() $k\colon {\mathbb Z}_p^{\ast }\rightarrow B^{\ast }$
is a B-valued weight as in Definition 3.6) tensored some period ring, in terms of overconvergent modular forms of weight
$k\colon {\mathbb Z}_p^{\ast }\rightarrow B^{\ast }$
is a B-valued weight as in Definition 3.6) tensored some period ring, in terms of overconvergent modular forms of weight
![]() $k+2$
, tensored with the same period ring. In [Reference Andreatta, Iovita and Stevens5] and in [Reference Andreatta, Iovita and Stevens6], we defined and studied Hodge-Tate Eichler-Shimura maps while in this article we’ll have Hodge–Tate, de Rham and crystalline variants.
$k+2$
, tensored with the same period ring. In [Reference Andreatta, Iovita and Stevens5] and in [Reference Andreatta, Iovita and Stevens6], we defined and studied Hodge-Tate Eichler-Shimura maps while in this article we’ll have Hodge–Tate, de Rham and crystalline variants.
To really explain what the main issues are that we deal with in this article, let us observe that there has been remarkable recent progress in p-adic Hodge theory and especially in integral p-adic Hodge theory, and let us just mention [Reference Bhatt, Morrow and Scholze8], [Reference Bhatt and Scholze9], [Reference Cesnavicius and Koshikawa11], [Reference Colmez, Dospinescu and Niziol14]. The articles quoted here deal with various cohomology theories on formal schemes or adic spaces with constant coefficients. On the other hand, it has been clear for some time that for applications to p-adic automorphic forms one needs to work with cohomology with very large coefficients. In this article, we try to understand p-adic Hodge theory (comparison morphisms really) with large coefficients, and therefore, unfortunately, we cannot use the recent results quoted above.
More precisely, let
![]() $\mathcal {X}:=\mathcal {X}_0(p^m, N)$
be the log adic space defined by the modular curve over
$\mathcal {X}:=\mathcal {X}_0(p^m, N)$
be the log adic space defined by the modular curve over
![]() ${\mathbb Q}_p$
associated to the congruence subgroup
${\mathbb Q}_p$
associated to the congruence subgroup
![]() $\Gamma _0(p^m) \cap \Gamma _1(N)$
. For any
$\Gamma _0(p^m) \cap \Gamma _1(N)$
. For any
![]() $r\ge 0$
, we have open subspaces
$r\ge 0$
, we have open subspaces
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^r}\bigr )$
, where
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^r}\bigr )$
, where
![]() $\mathrm {Ha}$
is a (any) local lift of the Hasse invariant. We fix
$\mathrm {Ha}$
is a (any) local lift of the Hasse invariant. We fix
![]() $k, B$
as above and let
$k, B$
as above and let
![]() $h\in {\mathbb N}$
. We denote by
$h\in {\mathbb N}$
. We denote by
![]() $\omega _E$
the sheaf of invariant differentials of the universal semiabelian scheme E over
$\omega _E$
the sheaf of invariant differentials of the universal semiabelian scheme E over
![]() $\mathcal {X}$
and by
$\mathcal {X}$
and by
![]() $\mathcal {X}_{\mathrm {pke}}$
, the log adic space
$\mathcal {X}_{\mathrm {pke}}$
, the log adic space
![]() $\mathcal {X}$
equipped with the pro-Kummer étale topology, see section §2.2. We let
$\mathcal {X}$
equipped with the pro-Kummer étale topology, see section §2.2. We let
![]() ${\mathbb D}_k$
denote the pro-Kummer étale sheaf of weight k-modular symbols on this
${\mathbb D}_k$
denote the pro-Kummer étale sheaf of weight k-modular symbols on this
![]() $\mathcal {X}_{\mathrm {pke}}$
, and we recall from [Reference Andreatta, Iovita and Stevens6] that both the pro-Kummer étale cohomology and the sheaf cohomology groups
$\mathcal {X}_{\mathrm {pke}}$
, and we recall from [Reference Andreatta, Iovita and Stevens6] that both the pro-Kummer étale cohomology and the sheaf cohomology groups
![]() $\mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}_k(1)\bigr )$
and
$\mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}_k(1)\bigr )$
and
![]() $\mathrm {H}^0\bigl ( \mathcal {X}\bigl (p/\mathrm {Ha}^{p^r}\bigr ), \omega _E^{k+2} \bigr )$
have finite slope decompositions for the action of the compact operator
$\mathrm {H}^0\bigl ( \mathcal {X}\bigl (p/\mathrm {Ha}^{p^r}\bigr ), \omega _E^{k+2} \bigr )$
have finite slope decompositions for the action of the compact operator
![]() $U_p$
. If
$U_p$
. If
![]() $h\in {\mathbb N}$
is a slope, we denote, for a Hecke module M by
$h\in {\mathbb N}$
is a slope, we denote, for a Hecke module M by
![]() $M^{(h)}$
the submodule of slope
$M^{(h)}$
the submodule of slope
![]() $\le h$
submodule of M.
$\le h$
submodule of M.
Then, Theorem 5.1 states that there is an r depending on k, and therefore a neighbourhood
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^r}\bigr )$
of a component of the ordinary locus in
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^r}\bigr )$
of a component of the ordinary locus in
![]() $\mathcal {X}$
, and a canonical
$\mathcal {X}$
, and a canonical
![]() ${\mathbb C}_p$
-linear, Galois and Hecke equivariant map:
${\mathbb C}_p$
-linear, Galois and Hecke equivariant map:
In a slightly different way and only for analytic weights, the map
![]() $\Psi _{\mathrm {HT,h}}$
was constructed in [Reference Andreatta, Iovita and Stevens5]. There we also proved that the map is generically surjective. The new result in this paper is:
$\Psi _{\mathrm {HT,h}}$
was constructed in [Reference Andreatta, Iovita and Stevens5]. There we also proved that the map is generically surjective. The new result in this paper is:
Theorem 1.1. If
![]() $\prod _{i=0}^{h-1}(u_k-i)\in \bigl (B[1/p]\bigr )^{\ast }$
, then
$\prod _{i=0}^{h-1}(u_k-i)\in \bigl (B[1/p]\bigr )^{\ast }$
, then
![]() $\Psi _{\mathrm {HT,h}}$
is surjective, for all
$\Psi _{\mathrm {HT,h}}$
is surjective, for all
![]() $h\ge 1$
, and it is surjective if
$h\ge 1$
, and it is surjective if
![]() $h=0$
.
$h=0$
.
Our next result in this article is a de Rham overconvergent Eichler–Shimura map. We fix now, as in section §6,
![]() $\mathcal {X}:=\mathcal {X}(N)$
the modular curve with full level N structure for the remainder of this introduction. We construct modular sheaves with connections and filtrations
$\mathcal {X}:=\mathcal {X}(N)$
the modular curve with full level N structure for the remainder of this introduction. We construct modular sheaves with connections and filtrations
![]() $\mathbf {W}_{k, \mathrm {dR}}$
on
$\mathbf {W}_{k, \mathrm {dR}}$
on
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^r}\bigr )$
, for an
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^r}\bigr )$
, for an
![]() $r\ge 0$
depending on k, which interpolate p-adically the family of sheaves
$r\ge 0$
depending on k, which interpolate p-adically the family of sheaves
![]() $\{\mathrm {Sym}^v\mathrm {H}^1_{\mathrm {dR}}\bigl (E/\mathcal {X} \bigr )\}_{v\in {\mathbb N}}$
, with their filtrations and connections, and we denote by
$\{\mathrm {Sym}^v\mathrm {H}^1_{\mathrm {dR}}\bigl (E/\mathcal {X} \bigr )\}_{v\in {\mathbb N}}$
, with their filtrations and connections, and we denote by
![]() $\displaystyle \mathbf {W}_{k, \mathrm {dR}, \bullet }: \mathbf {W}_{k, \mathrm {dR}}\stackrel {\nabla }{\longrightarrow }\mathbf {W}_{k+2, \mathrm {dR}}$
the de Rham complex of
$\displaystyle \mathbf {W}_{k, \mathrm {dR}, \bullet }: \mathbf {W}_{k, \mathrm {dR}}\stackrel {\nabla }{\longrightarrow }\mathbf {W}_{k+2, \mathrm {dR}}$
the de Rham complex of
![]() $(\mathbf {W}_{k, \mathrm {dR}}, \nabla )$
. Here, of course, we use the Kodaira–Spencer isomorphism in order to see the connection as a morphism of abelian sheaves with values in
$(\mathbf {W}_{k, \mathrm {dR}}, \nabla )$
. Here, of course, we use the Kodaira–Spencer isomorphism in order to see the connection as a morphism of abelian sheaves with values in
![]() $\mathbf {W}_{k+2, \mathrm {dR}}$
. Assuming the hypothesis and notations above we prove:
$\mathbf {W}_{k+2, \mathrm {dR}}$
. Assuming the hypothesis and notations above we prove:
Theorem 1.2.
a) There is a natural, Galois and Hecke equivariant
![]() $B\widehat {\otimes }B_{\mathrm {dR}}^+$
-semilinear map
$B\widehat {\otimes }B_{\mathrm {dR}}^+$
-semilinear map
b) If
![]() $\prod _{i=0}^{h-1}(u_k-i)\in \bigl (B[1/p]\bigr )^{\ast }$
then the display
$\prod _{i=0}^{h-1}(u_k-i)\in \bigl (B[1/p]\bigr )^{\ast }$
then the display
![]() $(\ast )$
above becomes:
$(\ast )$
above becomes:
and it is surjective.
In order to make it clear what improvements we were able to produce in this article, we now list the new ideas.
1) Neighbourhoods of the ordinary loci in modular curves.
Both in [Reference Andreatta, Iovita and Stevens5] and [Reference Andreatta, Iovita and Stevens6], we worked on the (log) adic modular curves
![]() $\mathcal {X}_1(N)$
and
$\mathcal {X}_1(N)$
and
![]() $\mathcal {X}_0(p, N)$
; these are the (log) adic spaces associated to the modular curves over
$\mathcal {X}_0(p, N)$
; these are the (log) adic spaces associated to the modular curves over
![]() ${\mathbb Q}_p$
of level
${\mathbb Q}_p$
of level
![]() $\Gamma _1(N)$
and, respectively
$\Gamma _1(N)$
and, respectively
![]() $\Gamma _1(N)\cap \Gamma _0(p)$
, which have a connected, respectively two connected, components of ordinary loci. We worked with strict neighbourhoods of these ordinary loci of depth
$\Gamma _1(N)\cap \Gamma _0(p)$
, which have a connected, respectively two connected, components of ordinary loci. We worked with strict neighbourhoods of these ordinary loci of depth
![]() $n\in {\mathbb N}$
defined as the points x with the property
$n\in {\mathbb N}$
defined as the points x with the property
![]() $v_x(\mathrm {Ha})\le 1/n$
. These neighbourhoods are defined over
$v_x(\mathrm {Ha})\le 1/n$
. These neighbourhoods are defined over
![]() $\mathrm {Spa}(L, {\cal O}_L)$
over which the point x is defined, where L is some complete extension of
$\mathrm {Spa}(L, {\cal O}_L)$
over which the point x is defined, where L is some complete extension of
![]() ${\mathbb Q}_p$
and these neighbourhoods are also used in this very article for the de Rham Eichler–Shimura maps.
${\mathbb Q}_p$
and these neighbourhoods are also used in this very article for the de Rham Eichler–Shimura maps.
For the Hodge–Tate comparison maps in this article, we use a better technology, inspired by the work of [Reference Chojecki, Hansen and Johansson12]. Namely, let
![]() $\mathcal {X}(p^{\infty }, N)$
be the perfectoid adic space over
$\mathcal {X}(p^{\infty }, N)$
be the perfectoid adic space over
![]() $\mathrm {Spa}({\mathbb C}_p, {\cal O}_{{\mathbb C}_p})$
associated to the projective limit of adic modular curves
$\mathrm {Spa}({\mathbb C}_p, {\cal O}_{{\mathbb C}_p})$
associated to the projective limit of adic modular curves
![]() $\displaystyle \lim _{\leftarrow , m}\mathcal {X}(p^m, N)$
and the Hodge–Tate period map
$\displaystyle \lim _{\leftarrow , m}\mathcal {X}(p^m, N)$
and the Hodge–Tate period map
We define interesting opens
![]() $U_{\#}^{(n)}\subset {\mathbb P}^1_{{\mathbb Q}_p}$
, for
$U_{\#}^{(n)}\subset {\mathbb P}^1_{{\mathbb Q}_p}$
, for
![]() $n\ge 1$
and the symbol
$n\ge 1$
and the symbol
![]() $\#\in \{0, \infty \}$
, which are invariant under the action of the m-th Iwahori subgroup
$\#\in \{0, \infty \}$
, which are invariant under the action of the m-th Iwahori subgroup
![]() $\mathrm {Iw}_m\subset \mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
as follows: If
$\mathrm {Iw}_m\subset \mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
as follows: If
![]() $\#=\infty $
, then
$\#=\infty $
, then
![]() $m\ge n$
if
$m\ge n$
if
![]() $\#=0$
, then
$\#=0$
, then
![]() $m\ge 1$
and on which we understand the dynamic of the
$m\ge 1$
and on which we understand the dynamic of the
![]() $U_p$
-operator. Then by the properties of
$U_p$
-operator. Then by the properties of
![]() $\pi _{\mathrm {HT}}$
, for every
$\pi _{\mathrm {HT}}$
, for every
![]() $n\ge 1$
, there are: an
$n\ge 1$
, there are: an
![]() $m\ge 1$
as above and neighbourhoods of the ordinary loci in
$m\ge 1$
as above and neighbourhoods of the ordinary loci in
![]() $\mathcal {X}_0(p^m, N)$
denoted
$\mathcal {X}_0(p^m, N)$
denoted
![]() ${\cal Z}_0^{(n)}, {\cal Z}_{\infty }^{(n)}$
such that if
${\cal Z}_0^{(n)}, {\cal Z}_{\infty }^{(n)}$
such that if
![]() $\pi _m\colon \mathcal {X}(p^{\infty }, N)\rightarrow \mathcal {X}_0(p^m, N)$
is the natural projection, then
$\pi _m\colon \mathcal {X}(p^{\infty }, N)\rightarrow \mathcal {X}_0(p^m, N)$
is the natural projection, then
![]() $\pi _{\mathrm {HT}}^{-1}(U_{\#}^{(n)})=\pi _m^{-1}({\cal Z}_{\#}^{(n)})$
, where
$\pi _{\mathrm {HT}}^{-1}(U_{\#}^{(n)})=\pi _m^{-1}({\cal Z}_{\#}^{(n)})$
, where
![]() $\#\in \{0, \infty \}$
such that we understand well the dynamic of the
$\#\in \{0, \infty \}$
such that we understand well the dynamic of the
![]() $U_p$
-operator on sections of modular sheaves on
$U_p$
-operator on sections of modular sheaves on
![]() $\mathcal {X}_0(p^m, N)$
. We remark that
$\mathcal {X}_0(p^m, N)$
. We remark that
![]() $\mathcal {X}_0(p^m, N)$
has many connected components of the ordinary locus if m is large and a complicated semistable integral model; therefore, it would have been difficult to apply the previous method, that is, defining neighbourhoods of the ordinary loci using
$\mathcal {X}_0(p^m, N)$
has many connected components of the ordinary locus if m is large and a complicated semistable integral model; therefore, it would have been difficult to apply the previous method, that is, defining neighbourhoods of the ordinary loci using
![]() $\mathrm {Ha}$
, in
$\mathrm {Ha}$
, in
![]() $\mathcal {X}_0(p^m, N)$
for
$\mathcal {X}_0(p^m, N)$
for
![]() $m>1$
.
$m>1$
.
2) Payman Kassaei’s method for the cohomology of pro-Kummer étale sheaves.
Let us now explain our new take on the overconvergent Hodge–Tate Eichler–Shimura morphism. We fix a slope
![]() $h\in {\mathbb N}$
and a weight
$h\in {\mathbb N}$
and a weight
![]() $k\colon {\mathbb Z}_p^{\ast }\longrightarrow B^{\ast }$
as in Definition 3.6. This weight is N-analytic, for some
$k\colon {\mathbb Z}_p^{\ast }\longrightarrow B^{\ast }$
as in Definition 3.6. This weight is N-analytic, for some
![]() $N\in {\mathbb N}$
, that is, there is
$N\in {\mathbb N}$
, that is, there is
![]() $u_k\in B[1/p]$
such that
$u_k\in B[1/p]$
such that
![]() $k(t)=\mathrm {exp}\bigl (u_k\log (t)\bigr )$
for all
$k(t)=\mathrm {exp}\bigl (u_k\log (t)\bigr )$
for all
![]() $t\in 1+p^N{\mathbb Z}_p$
. These data determine integers
$t\in 1+p^N{\mathbb Z}_p$
. These data determine integers
![]() $n, u, m$
such that on
$n, u, m$
such that on
![]() $\mathcal {X}:=\mathcal {X}_0(p^m, N)$
we have our neighbourhoods
$\mathcal {X}:=\mathcal {X}_0(p^m, N)$
we have our neighbourhoods
![]() ${\cal Z}_{\infty }^{(u)}$
for
${\cal Z}_{\infty }^{(u)}$
for
![]() $u\le m$
and
$u\le m$
and
![]() ${\cal Z}_0^{(n)}, {\cal Z}_0^{(n+1)}$
. We base-change
${\cal Z}_0^{(n)}, {\cal Z}_0^{(n+1)}$
. We base-change
![]() $\mathcal {X}, {\cal Z}_{\infty }^{(u)}, {\cal Z}_0^{(n)}, {\cal Z}_0^{(n+1)}$
over
$\mathcal {X}, {\cal Z}_{\infty }^{(u)}, {\cal Z}_0^{(n)}, {\cal Z}_0^{(n+1)}$
over
![]() $\mathrm {Spa}({\mathbb Q}_p, {\mathbb Z}_p)$
to
$\mathrm {Spa}({\mathbb Q}_p, {\mathbb Z}_p)$
to
![]() $\mathrm {Spa}(B[1/p], B)$
and still denote them
$\mathrm {Spa}(B[1/p], B)$
and still denote them
![]() $\mathcal {X}, {\cal Z}_{\infty }^{(u)}, {\cal Z}_0^{(n)}, {\cal Z}_0^{(n+1)}$
. We let
$\mathcal {X}, {\cal Z}_{\infty }^{(u)}, {\cal Z}_0^{(n)}, {\cal Z}_0^{(n+1)}$
. We let
![]() ${\mathbb D}_k^o$
be the integral sheaf of weight k-distributions, seen as a pro-Kummer étale sheaf on
${\mathbb D}_k^o$
be the integral sheaf of weight k-distributions, seen as a pro-Kummer étale sheaf on
![]() $\mathcal {X}$
, and denote by
$\mathcal {X}$
, and denote by
![]() ${\mathbb D}_k:={\mathbb D}_k^o\otimes _{{\mathbb Z}_p}{\mathbb Q}_p$
.
${\mathbb D}_k:={\mathbb D}_k^o\otimes _{{\mathbb Z}_p}{\mathbb Q}_p$
.
First, let us recall that the map
![]() $\Psi _{\mathrm {HT,h}}$
appears, after passing to the the open subspaces defined in (1), as the following composition:
$\Psi _{\mathrm {HT,h}}$
appears, after passing to the the open subspaces defined in (1), as the following composition:
 $$ \begin{align*} \mathrm{H}^1\bigl(\mathcal{X}_{\mathrm{pke}}, {\mathbb D}_k(1) \bigr)^{(h)}\widehat{\otimes}{\mathbb C}_p&\cong \Bigl(\mathrm{ H}^1\bigl(\mathcal{X}_{\mathrm{pke}}, {\mathfrak{D}}_k (1) \bigr)[1/p]\Bigr)^{(h)}\\&\quad \stackrel{\mathcal{R}}{\longrightarrow}\Bigl(\mathrm{ H}^1\bigl(({\cal Z}_{\infty}^{(u)})_{\mathrm{pke}}, {\mathfrak{D}}_k(1)\bigr)[1/p]\Bigr)^{(h)}\stackrel{\Phi}{\longrightarrow} \end{align*} $$
$$ \begin{align*} \mathrm{H}^1\bigl(\mathcal{X}_{\mathrm{pke}}, {\mathbb D}_k(1) \bigr)^{(h)}\widehat{\otimes}{\mathbb C}_p&\cong \Bigl(\mathrm{ H}^1\bigl(\mathcal{X}_{\mathrm{pke}}, {\mathfrak{D}}_k (1) \bigr)[1/p]\Bigr)^{(h)}\\&\quad \stackrel{\mathcal{R}}{\longrightarrow}\Bigl(\mathrm{ H}^1\bigl(({\cal Z}_{\infty}^{(u)})_{\mathrm{pke}}, {\mathfrak{D}}_k(1)\bigr)[1/p]\Bigr)^{(h)}\stackrel{\Phi}{\longrightarrow} \end{align*} $$
where
![]() ${\mathfrak {D}}_k:={\mathbb D}_k\widehat {\otimes }{\cal O}_{{\cal Z}_{\mathrm {pke}}}$
,
${\mathfrak {D}}_k:={\mathbb D}_k\widehat {\otimes }{\cal O}_{{\cal Z}_{\mathrm {pke}}}$
,
![]() $\mathcal {R}$
is the restriction map and
$\mathcal {R}$
is the restriction map and
![]() $\Phi $
was defined in [Reference Andreatta, Iovita and Stevens6] and in 4.15, and it was proved in loc. cit. that it is an isomorphism. Therefore, in order to prove Theorem 5.1, we need to show that restriction from
$\Phi $
was defined in [Reference Andreatta, Iovita and Stevens6] and in 4.15, and it was proved in loc. cit. that it is an isomorphism. Therefore, in order to prove Theorem 5.1, we need to show that restriction from
![]() ${\cal Z}_{\mathrm {pke}}$
to
${\cal Z}_{\mathrm {pke}}$
to
![]() $({\cal Z}_{\infty }^{(u)})_{\mathrm {pke}}$
induces a surjective map on the
$({\cal Z}_{\infty }^{(u)})_{\mathrm {pke}}$
induces a surjective map on the
![]() $\mathrm {H}^1$
’s if
$\mathrm {H}^1$
’s if
![]() $\prod _{i-0}^{h-1}(u_k-i)$
is a unit in
$\prod _{i-0}^{h-1}(u_k-i)$
is a unit in
![]() $B[1/p]$
.
$B[1/p]$
.
To do this, we use Payman Kassaei’s idea of proving classicity of overconvergent modular forms of integral weight and small slope. More precisely, given
![]() $x\in \mathrm {H}^1\bigl (({\cal Z}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )^{(h)}$
, we may see it as an element of
$x\in \mathrm {H}^1\bigl (({\cal Z}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )^{(h)}$
, we may see it as an element of
![]() $\mathrm {H}^1\bigl (({\cal Z}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o\ \bigr )$
which is annihilated by
$\mathrm {H}^1\bigl (({\cal Z}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o\ \bigr )$
which is annihilated by
![]() $Q(U_p)$
, where
$Q(U_p)$
, where
![]() $Q(T)\in (B\widehat {\otimes }{\cal O}_{{\mathbb C}_p})[T]$
is a polynomial all of whose roots have valuations
$Q(T)\in (B\widehat {\otimes }{\cal O}_{{\mathbb C}_p})[T]$
is a polynomial all of whose roots have valuations
![]() $\le h$
. We write
$\le h$
. We write
![]() $Q(T)=P(T)-\alpha $
, with
$Q(T)=P(T)-\alpha $
, with
![]() $P(0)=0$
, and denote by a the valuation of
$P(0)=0$
, and denote by a the valuation of
![]() $\alpha $
. Then by applying to x the operator
$\alpha $
. Then by applying to x the operator
![]() $\bigl (P(U_p)\bigr )^{n+u+1}$
we can see it as a class
$\bigl (P(U_p)\bigr )^{n+u+1}$
we can see it as a class
![]() $\tilde {x}$
in
$\tilde {x}$
in
![]() $\mathrm {H}^1\bigl ((\mathcal {X}\backslash {\cal Z}_0^{(n+1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o\bigr )$
. On the other hand, following Kassaei, we can define a new operator
$\mathrm {H}^1\bigl ((\mathcal {X}\backslash {\cal Z}_0^{(n+1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o\bigr )$
. On the other hand, following Kassaei, we can define a new operator
![]() $\bigl (P(U_p)^{n} \bigr )^{\mathrm {good}}$
by choosing all the isogenies defining the correspondence
$\bigl (P(U_p)^{n} \bigr )^{\mathrm {good}}$
by choosing all the isogenies defining the correspondence
![]() $U_p^{n}$
which map
$U_p^{n}$
which map
![]() ${\cal Z}_0^{(n)}$
to
${\cal Z}_0^{(n)}$
to
![]() ${\cal Z}_{\infty }^{(1)}$
. Let
${\cal Z}_{\infty }^{(1)}$
. Let
![]() $\mathcal {P}(x):=\bigl (P(U_p)^{n}\bigr )^{\mathrm {good}}\bigl (P(U_p)^{u+1}(x)\bigr )\in \mathrm {H}^1\bigl ({\cal Z}_0^{(n)}, {\mathfrak {D}}_k^o\bigr )$
. As the family
$\mathcal {P}(x):=\bigl (P(U_p)^{n}\bigr )^{\mathrm {good}}\bigl (P(U_p)^{u+1}(x)\bigr )\in \mathrm {H}^1\bigl ({\cal Z}_0^{(n)}, {\mathfrak {D}}_k^o\bigr )$
. As the family
![]() $\{\mathcal {X}\backslash {\cal Z}_0^{(n+1)}, {\cal Z}_0^{(n)}\}$
is an open covering of
$\{\mathcal {X}\backslash {\cal Z}_0^{(n+1)}, {\cal Z}_0^{(n)}\}$
is an open covering of
![]() $\mathcal {X}$
, one can use a Mayer–Vietoris sequence in order to glue
$\mathcal {X}$
, one can use a Mayer–Vietoris sequence in order to glue
![]() $p^s\tilde {x}, p^s\mathcal {P}(x)$
for a certain fixed power of p, s modulo
$p^s\tilde {x}, p^s\mathcal {P}(x)$
for a certain fixed power of p, s modulo
![]() $p^r$
, where r was chosen in the beginning large enough so that
$p^r$
, where r was chosen in the beginning large enough so that
![]() $r\ge 2(s+d+1+(u+n+1)a)$
for a certain constant d (see Section §5). We obtain a class
$r\ge 2(s+d+1+(u+n+1)a)$
for a certain constant d (see Section §5). We obtain a class
![]() $z\in \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathfrak {D}}_k^0 \bigr )$
annihilated by
$z\in \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathfrak {D}}_k^0 \bigr )$
annihilated by
![]() $Q(U_p)$
and such that its restriction to
$Q(U_p)$
and such that its restriction to
![]() ${\cal Z}_{\infty }^{(n)}$
is congruent to
${\cal Z}_{\infty }^{(n)}$
is congruent to
![]() $p^{s+d+1}\alpha ^{u+n+1}x$
modulo
$p^{s+d+1}\alpha ^{u+n+1}x$
modulo
![]() $p^r$
, that is, there is
$p^r$
, that is, there is
![]() $x_1\in \mathrm {H}^1\bigl (({\cal Z}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o\bigr )$
annihilated by
$x_1\in \mathrm {H}^1\bigl (({\cal Z}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o\bigr )$
annihilated by
![]() $Q(U_p)$
such that
$Q(U_p)$
such that
![]() $\mathcal {R}(z)=p^{s+d+1}\alpha ^{n+u+1}(x-p^{r/2}x_1)$
. Now, we iterate the process for
$\mathcal {R}(z)=p^{s+d+1}\alpha ^{n+u+1}(x-p^{r/2}x_1)$
. Now, we iterate the process for
![]() $x_1$
and in the end obtain an element
$x_1$
and in the end obtain an element
![]() $y\in \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )^{(h)}$
such that
$y\in \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )^{(h)}$
such that
![]() $\mathcal {R}(y)=x$
.
$\mathcal {R}(y)=x$
.
3) On the de Rham comparison.
It is interesting to note, about the de Rham Eichler–Shimura map
![]() $\rho _k$
in theorem 1.2, the ‘decalage’ between the filtrations on
$\rho _k$
in theorem 1.2, the ‘decalage’ between the filtrations on
![]() $B_{\mathrm {dR}}$
that appear. This decalage is explained as follows: On the pro-Kummer étale site of
$B_{\mathrm {dR}}$
that appear. This decalage is explained as follows: On the pro-Kummer étale site of
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^r}\bigr )$
, we have the sheaves with filtrations and connections:
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^r}\bigr )$
, we have the sheaves with filtrations and connections:
![]() $\nabla '\colon \mathbf {W}_{k, \mathrm {dR}}\widehat {\otimes }{\cal O}\mathbb {B}_{\mathrm {dR}}\longrightarrow \mathbf {W}_{k+2, \mathrm {dR}}\widehat {\otimes }{\cal O}\mathbb {B}_{\mathrm {dR}}$
(see Section §6.4 for the details), where
$\nabla '\colon \mathbf {W}_{k, \mathrm {dR}}\widehat {\otimes }{\cal O}\mathbb {B}_{\mathrm {dR}}\longrightarrow \mathbf {W}_{k+2, \mathrm {dR}}\widehat {\otimes }{\cal O}\mathbb {B}_{\mathrm {dR}}$
(see Section §6.4 for the details), where
![]() $\nabla '=\nabla _k\widehat {\otimes }1 + 1\widehat {\otimes }\nabla _{\mathrm {dR}}$
and
$\nabla '=\nabla _k\widehat {\otimes }1 + 1\widehat {\otimes }\nabla _{\mathrm {dR}}$
and
![]() $\mathbf {W}_{k, \mathrm {dR}}$
has an increasing, infinite filtration, while
$\mathbf {W}_{k, \mathrm {dR}}$
has an increasing, infinite filtration, while
![]() ${\cal O}\mathbb {B}_{\mathrm {dR}}$
has a decreasing, infinite filtration. Both
${\cal O}\mathbb {B}_{\mathrm {dR}}$
has a decreasing, infinite filtration. Both
![]() $\nabla _k$
and
$\nabla _k$
and
![]() $\nabla _{\mathrm {dR}}$
satisfy the Griffith transversality property with respect to the respective filtrations, but on the tensor product, we don’t have a natural filtration. We have, however, the following fact:
$\nabla _{\mathrm {dR}}$
satisfy the Griffith transversality property with respect to the respective filtrations, but on the tensor product, we don’t have a natural filtration. We have, however, the following fact:
This explains the decalage.
As an immediate consequence of the above theorem, we have a ‘big exponential map’. More precisely, let K be the finite extension of
![]() ${\mathbb Q}_p$
over which
${\mathbb Q}_p$
over which
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^r}\bigr )$
are both defined, and let G denote the absolute Galois group of K for a fixed algebraic closure
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^r}\bigr )$
are both defined, and let G denote the absolute Galois group of K for a fixed algebraic closure
![]() $\overline {K}$
of K.
$\overline {K}$
of K.
Then we have a Hecke equivariant, B-linear map
which has the property that, for every classical weight
![]() $k_0$
-specialization, it is compatible with the classical dual exponential map, as follows:
$k_0$
-specialization, it is compatible with the classical dual exponential map, as follows:
a) If
![]() $k_0>h-1$
, that is,
$k_0>h-1$
, that is,
![]() $k_0$
is a noncritical weight for the slope h, then we have the following commutative diagram with horizontal isomorphisms. Here, we denoted by
$k_0$
is a noncritical weight for the slope h, then we have the following commutative diagram with horizontal isomorphisms. Here, we denoted by
![]() $\exp ^{\ast }_{k_0}$
the Kato dual exponential map associated to weight
$\exp ^{\ast }_{k_0}$
the Kato dual exponential map associated to weight
![]() $k_0$
modular forms.
$k_0$
modular forms.
 $$ \begin{align*}\begin{array}{ccccccccc} \Bigl(\mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k(1) \bigr)^{(h)}\right)\Bigr)_{k_0}&\stackrel{\bigl(\mathrm{Exp}^{\ast}_k\bigr)_{k_0}}{\longrightarrow} &\!\!\Bigl(\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^r}\bigr), \mathbf{W}_{k, \mathrm{dR}, \bullet}\bigr)^{ (h)}\Bigr)_{k_0}\\ \downarrow \cong&&\downarrow\cong\\ \mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, \mathrm{Sym}^{k_0}(T_p(E)^{\vee})(1)\bigr)^{(h)}\right)&\stackrel{\exp^{\ast}_{k_0}}{\longrightarrow} &\mathrm{Fil}^0\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}, \mathrm{Sym}^{k_0}(\mathrm{H}_E)\bigr)^{(h)}. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccccccccc} \Bigl(\mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k(1) \bigr)^{(h)}\right)\Bigr)_{k_0}&\stackrel{\bigl(\mathrm{Exp}^{\ast}_k\bigr)_{k_0}}{\longrightarrow} &\!\!\Bigl(\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^r}\bigr), \mathbf{W}_{k, \mathrm{dR}, \bullet}\bigr)^{ (h)}\Bigr)_{k_0}\\ \downarrow \cong&&\downarrow\cong\\ \mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, \mathrm{Sym}^{k_0}(T_p(E)^{\vee})(1)\bigr)^{(h)}\right)&\stackrel{\exp^{\ast}_{k_0}}{\longrightarrow} &\mathrm{Fil}^0\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}, \mathrm{Sym}^{k_0}(\mathrm{H}_E)\bigr)^{(h)}. \end{array} \end{align*} $$
b) If
![]() $0\le k_0\le h+1$
, that is,
$0\le k_0\le h+1$
, that is,
![]() $k_0$
is critical with respect to b, we only have a commutative diagram of the form
$k_0$
is critical with respect to b, we only have a commutative diagram of the form
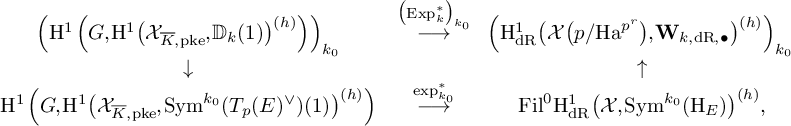 $$ \begin{align*} \begin{array}{ccccccccc} \Bigl(\mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k(1) \bigr)^{(h)}\right)\Bigr)_{k_0}&\stackrel{\bigl(\mathrm{Exp}^{\ast}_k\bigr)_{k_0}}{\longrightarrow} &\!\!\Bigl(\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^r}\bigr), \mathbf{W}_{k, \mathrm{dR}, \bullet}\bigr)^{ (h)}\Bigr)_{k_0}\\ \downarrow &&\uparrow\\ \mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, \mathrm{Sym}^{k_0}(T_p(E)^{\vee})(1)\bigr)^{(h)}\right)&\stackrel{\exp^{\ast}_{k_0}}{\longrightarrow} &\mathrm{Fil}^0\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}, \mathrm{Sym}^{k_0}(\mathrm{H}_E)\bigr)^{(h)}, \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ccccccccc} \Bigl(\mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k(1) \bigr)^{(h)}\right)\Bigr)_{k_0}&\stackrel{\bigl(\mathrm{Exp}^{\ast}_k\bigr)_{k_0}}{\longrightarrow} &\!\!\Bigl(\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^r}\bigr), \mathbf{W}_{k, \mathrm{dR}, \bullet}\bigr)^{ (h)}\Bigr)_{k_0}\\ \downarrow &&\uparrow\\ \mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, \mathrm{Sym}^{k_0}(T_p(E)^{\vee})(1)\bigr)^{(h)}\right)&\stackrel{\exp^{\ast}_{k_0}}{\longrightarrow} &\mathrm{Fil}^0\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}, \mathrm{Sym}^{k_0}(\mathrm{H}_E)\bigr)^{(h)}, \end{array} \end{align*} $$
where the right vertical arrow is induced by restriction.
2 Preliminaries
We will denote by X, Y, Z,
![]() $\ldots $
log schemes and by caligraphic letters
$\ldots $
log schemes and by caligraphic letters
![]() $\mathcal {X}$
,
$\mathcal {X}$
,
![]() $\mathcal {Y}$
,
$\mathcal {Y}$
,
![]() ${\cal Z}$
,
${\cal Z}$
,
![]() $\ldots $
log adic spaces. We refer to [Reference Diao, Lan, Liu and Zhu15] for generalities on those.
$\ldots $
log adic spaces. We refer to [Reference Diao, Lan, Liu and Zhu15] for generalities on those.
2.1 Pro-Kummer étale site
Given a finite saturated (for short ‘fs’) locally noetherian log scheme X (resp. an fs locally noetherian log adic space
![]() $\mathcal {X}$
) we denote by
$\mathcal {X}$
) we denote by
![]() $X_{\mathrm {ket}}$
,
$X_{\mathrm {ket}}$
,
![]() $X_{\mathrm {fket}}$
(resp.
$X_{\mathrm {fket}}$
(resp.
![]() $\mathcal {X}_{\mathrm {ket}}$
,
$\mathcal {X}_{\mathrm {ket}}$
,
![]() $\mathcal {X}_{\mathrm {fket}}$
) the Kummer étale site, respectively the finite Kummer étale site (see [Reference Illusie18, Def. 2.1], [Reference Diao, Lan, Liu and Zhu15, Def. 4.1.2]). Following Scholze [Reference Scholze22], we denote by
$\mathcal {X}_{\mathrm {fket}}$
) the Kummer étale site, respectively the finite Kummer étale site (see [Reference Illusie18, Def. 2.1], [Reference Diao, Lan, Liu and Zhu15, Def. 4.1.2]). Following Scholze [Reference Scholze22], we denote by
![]() $X_{\mathrm {pke}}$
, resp.
$X_{\mathrm {pke}}$
, resp.
![]() $X_{\mathrm {profket}}$
(resp.
$X_{\mathrm {profket}}$
(resp.
![]() $\mathcal {X}_{\mathrm {pke}}$
,
$\mathcal {X}_{\mathrm {pke}}$
,
![]() $\mathcal {X}_{\mathrm {profket}}$
) the pro-Kummer étale site, resp. the pro-finite Kummer étale site (see [Reference Diao, Lan, Liu and Zhu15, Def. 5.1.2 & 5.1.9]) of X, respectively
$\mathcal {X}_{\mathrm {profket}}$
) the pro-Kummer étale site, resp. the pro-finite Kummer étale site (see [Reference Diao, Lan, Liu and Zhu15, Def. 5.1.2 & 5.1.9]) of X, respectively
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
As a category, it is the full subcategory of pro-
![]() $X_{\mathrm {ket}}$
, resp. pro-
$X_{\mathrm {ket}}$
, resp. pro-
![]() $X_{\mathrm {fket}}$
(resp. pro-
$X_{\mathrm {fket}}$
(resp. pro-
![]() $\mathcal {X}_{\mathrm {ket}}$
, pro-
$\mathcal {X}_{\mathrm {ket}}$
, pro-
![]() $\mathcal {X}_{\mathrm {fket}}$
) of pro-objects that are pro-Kummer étale over X, resp. pro-finite Kummer étale over X (resp.
$\mathcal {X}_{\mathrm {fket}}$
) of pro-objects that are pro-Kummer étale over X, resp. pro-finite Kummer étale over X (resp.
![]() $\mathcal {X}$
), that is, objects that are equivalent to cofiltered systems
$\mathcal {X}$
), that is, objects that are equivalent to cofiltered systems
![]() $\displaystyle {\lim _{\leftarrow }} Z_i$
such that
$\displaystyle {\lim _{\leftarrow }} Z_i$
such that
![]() $Z_i\to X$
is Kummer étale, resp. finite Kummer étale, for every i and there exists an index
$Z_i\to X$
is Kummer étale, resp. finite Kummer étale, for every i and there exists an index
![]() $i_0$
such that
$i_0$
such that
![]() $Z_j\to Z_i$
is finite Kummer étale and surjective for i and
$Z_j\to Z_i$
is finite Kummer étale and surjective for i and
![]() $j\geq i_0$
(and similarly for
$j\geq i_0$
(and similarly for
![]() $\mathcal {X}$
). For the covering families we refer to loc. cit.
$\mathcal {X}$
). For the covering families we refer to loc. cit.
We have a natural projection
![]() $\nu \colon X_{\mathrm {pke}}\to X_{\mathrm {ket}}$
(resp.
$\nu \colon X_{\mathrm {pke}}\to X_{\mathrm {ket}}$
(resp.
![]() $\nu \colon \mathcal {X}_{\mathrm {pke}}\to \mathcal {X}_{\mathrm {ket}}$
) sending
$\nu \colon \mathcal {X}_{\mathrm {pke}}\to \mathcal {X}_{\mathrm {ket}}$
) sending
![]() $U\in X_{\mathrm {ket}}$
(resp. in
$U\in X_{\mathrm {ket}}$
(resp. in
![]() $\mathcal {X}_{\mathrm {ket}}$
) to the constant inverse system defined by U. Then, by [Reference Diao, Lan, Liu and Zhu15, Prop. 5.1.6 & 5.1.7] for every sheaf of abelian groups
$\mathcal {X}_{\mathrm {ket}}$
) to the constant inverse system defined by U. Then, by [Reference Diao, Lan, Liu and Zhu15, Prop. 5.1.6 & 5.1.7] for every sheaf of abelian groups
![]() ${\cal F}$
on
${\cal F}$
on
![]() $X_{\mathrm {ket}}$
(resp. in
$X_{\mathrm {ket}}$
(resp. in
![]() $\mathcal {X}_{\mathrm {ket}}$
) and any quasi-compact and quasi-separated object
$\mathcal {X}_{\mathrm {ket}}$
) and any quasi-compact and quasi-separated object
![]() $U={\displaystyle {\lim _{\leftarrow }}} U_j$
in
$U={\displaystyle {\lim _{\leftarrow }}} U_j$
in
![]() $X_{\mathrm {pke}}$
(resp. in
$X_{\mathrm {pke}}$
(resp. in
![]() $\mathcal {X}_{\mathrm {pke}}$
), we have natural isomorphisms of
$\mathcal {X}_{\mathrm {pke}}$
), we have natural isomorphisms of
![]() $\delta $
-functors
$\delta $
-functors
2.2 Sheaves on the pro-Kummer étale site
We then have the following sheaves on
![]() $\mathcal {X}_{{\mathrm {pke}}}$
defined in [Reference Diao, Lan, Liu and Zhu15, Def. 5.4.1] and in [Reference Diao, Lan, Liu and Zhu16, Def. 2.2.3] following [Reference Scholze22, Def. 6.1]:
$\mathcal {X}_{{\mathrm {pke}}}$
defined in [Reference Diao, Lan, Liu and Zhu15, Def. 5.4.1] and in [Reference Diao, Lan, Liu and Zhu16, Def. 2.2.3] following [Reference Scholze22, Def. 6.1]:
-
i. The structure sheaf
 ${\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}:=\nu ^{-1}\bigl ({\cal O}_{\mathcal {X}_{\mathrm {ket}}}\bigr )$
and its subsheaf of integral elements
${\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}:=\nu ^{-1}\bigl ({\cal O}_{\mathcal {X}_{\mathrm {ket}}}\bigr )$
and its subsheaf of integral elements
 ${\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+:=\nu ^{-1}\bigl ({\cal O}_{\mathcal {X}_{\mathrm {ket}}}^+\bigr )$
. It comes endowed with a morphism of sheaves of multiplicative monoids
${\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+:=\nu ^{-1}\bigl ({\cal O}_{\mathcal {X}_{\mathrm {ket}}}^+\bigr )$
. It comes endowed with a morphism of sheaves of multiplicative monoids
 $\alpha \colon {\cal M} \to {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}$
defined by taking
$\alpha \colon {\cal M} \to {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}$
defined by taking
 $\nu ^{-1}$
of the morphism of sheaves of multiplicative monoids defining the log structure on
$\nu ^{-1}$
of the morphism of sheaves of multiplicative monoids defining the log structure on
 $\mathcal {X}$
.
$\mathcal {X}$
. -
ii. The completed sheaf
 $\widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+:=\displaystyle {\lim _{\infty \leftarrow n}} {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+/p^n {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
and the completed structure sheaf
$\widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+:=\displaystyle {\lim _{\infty \leftarrow n}} {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+/p^n {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
and the completed structure sheaf
 $ \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}:=\widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+\bigl [ \frac {1}{p}\bigr ]$
.
$ \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}:=\widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+\bigl [ \frac {1}{p}\bigr ]$
. -
iii. Let K be a perfectoid field of characteristic
 $0$
with an open and bounded subring
$0$
with an open and bounded subring
 $K^+$
. Assume that
$K^+$
. Assume that
 $\mathcal {X}$
is defined over
$\mathcal {X}$
is defined over
 $\mathrm {Spa}(K,K^+)$
. Then we have the tilted integral structure sheaf
$\mathrm {Spa}(K,K^+)$
. Then we have the tilted integral structure sheaf
 $\widehat {{\cal O}}_{\mathcal {X}^{\flat }_{{\mathrm {pke}}}}^+:= \displaystyle {\lim _{\leftarrow \varphi }} {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+/p {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
and the tilted structure sheaf
$\widehat {{\cal O}}_{\mathcal {X}^{\flat }_{{\mathrm {pke}}}}^+:= \displaystyle {\lim _{\leftarrow \varphi }} {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+/p {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
and the tilted structure sheaf
 $\widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}^{\flat }}:=\widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}^{\flat }}^+\otimes _{K^{\flat +}} K^{\flat }$
. It comes endowed with a morphism of monoids
$\widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}^{\flat }}:=\widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}^{\flat }}^+\otimes _{K^{\flat +}} K^{\flat }$
. It comes endowed with a morphism of monoids
 $\alpha ^{\flat } \colon {\cal M}^{\flat } \to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}^{\flat }}$
, where
$\alpha ^{\flat } \colon {\cal M}^{\flat } \to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}^{\flat }}$
, where
 ${\cal M}^{\flat }$
is the inverse limit
${\cal M}^{\flat }$
is the inverse limit
 $\displaystyle {\lim _{\leftarrow }} {\cal M}$
indexed by
$\displaystyle {\lim _{\leftarrow }} {\cal M}$
indexed by
 ${\mathbb N}$
with transition maps given by raising to the p-th power,
${\mathbb N}$
with transition maps given by raising to the p-th power,
 $\widehat {{\cal O}}_{\mathcal {X}^{\flat }}$
is identified as a sheaf of mutiplicative monoids with the inverse limit
$\widehat {{\cal O}}_{\mathcal {X}^{\flat }}$
is identified as a sheaf of mutiplicative monoids with the inverse limit
 $\displaystyle {\lim _{\leftarrow }} \widehat { {\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}$
indexed by
$\displaystyle {\lim _{\leftarrow }} \widehat { {\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}$
indexed by
 ${\mathbb N}$
with transition maps given by rasing to the p-th power and the map
${\mathbb N}$
with transition maps given by rasing to the p-th power and the map
 $\alpha ^{\flat }$
is the inverse limit of the maps
$\alpha ^{\flat }$
is the inverse limit of the maps
 $\alpha $
composed with the natural maps
$\alpha $
composed with the natural maps
 ${ {\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}\to \widehat { {\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}$
.
${ {\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}\to \widehat { {\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}$
. -
iv. The period sheaf
 $\mathbb {A}_{\mathrm {inf}}:=\mathrm {W}\bigl (\widehat {{\cal O}}_{\mathcal {X}^{\flat }_{{\mathrm {pke}}}}^+ \bigr )$
and the period map
$\mathbb {A}_{\mathrm {inf}}:=\mathrm {W}\bigl (\widehat {{\cal O}}_{\mathcal {X}^{\flat }_{{\mathrm {pke}}}}^+ \bigr )$
and the period map
 $\vartheta \colon \mathbb {A}_{\mathrm {inf}}\to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
.
$\vartheta \colon \mathbb {A}_{\mathrm {inf}}\to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
.
2.3 Log affinoid perfectoid opens
Consider a locally noetherian fs log adic space
![]() $\mathcal {X}$
over
$\mathcal {X}$
over
![]() $\mathrm {Spa}({\mathbb Q}_p,{\mathbb Z}_p)$
. Following [Reference Diao, Lan, Liu and Zhu15, Def. 5.3.1 & Rmk. 5.3.2], an object
$\mathrm {Spa}({\mathbb Q}_p,{\mathbb Z}_p)$
. Following [Reference Diao, Lan, Liu and Zhu15, Def. 5.3.1 & Rmk. 5.3.2], an object
![]() $U=\lim _{i\in I} U_i$
, with
$U=\lim _{i\in I} U_i$
, with
![]() $U_i=\bigl (\mathrm {Spa}(R_i,R_i^+),{\cal M}_i\bigr )$
in
$U_i=\bigl (\mathrm {Spa}(R_i,R_i^+),{\cal M}_i\bigr )$
in
![]() $\mathcal {X}_{\mathrm {pke}}$
is called log affinoid perfectoid if:
$\mathcal {X}_{\mathrm {pke}}$
is called log affinoid perfectoid if:
-
a. There is an initial object
 $0 \in I$
.
$0 \in I$
. -
b. Each
 $U_i$
admits a global sharp finite saturated chart
$U_i$
admits a global sharp finite saturated chart
 $P_i$
such that each transition map
$P_i$
such that each transition map
 $U_j\to U_i$
is modeled on the Kummer chart
$U_j\to U_i$
is modeled on the Kummer chart
 $P_i \to P_j$
;
$P_i \to P_j$
; -
c.
 $\bigl (\mathrm {Spa}(R_i,R_i^+)\bigr )_i$
is affinoid perfectoid, that is, the p-adic completion
$\bigl (\mathrm {Spa}(R_i,R_i^+)\bigr )_i$
is affinoid perfectoid, that is, the p-adic completion
 $(R,R^+)$
of
$(R,R^+)$
of
 $\lim _i (R_i,R_i^+)$
is a perfectoid affinoid
$\lim _i (R_i,R_i^+)$
is a perfectoid affinoid
 ${\mathbb Q}_p$
-algebra;
${\mathbb Q}_p$
-algebra; -
d. The monoid
 $P = \lim _i P_i$
is n-divisible for all n.
$P = \lim _i P_i$
is n-divisible for all n.
Given a log affinoid perfectoid U as above, we denote by
![]() $\widehat {U}:=\mathrm {Spa}\bigl (R,R^+\bigr )$
the associated perfectoid affinoid space. By [Reference Diao, Lan, Liu and Zhu15, Lemma 5.3.6], it has the same underlying topological space as U (which is defined as the inverse limit of topological spaces
$\widehat {U}:=\mathrm {Spa}\bigl (R,R^+\bigr )$
the associated perfectoid affinoid space. By [Reference Diao, Lan, Liu and Zhu15, Lemma 5.3.6], it has the same underlying topological space as U (which is defined as the inverse limit of topological spaces
![]() $\displaystyle \lim _{\leftarrow \ i} \vert U_i\vert $
). Moreover, by [Reference Diao, Lan, Liu and Zhu15, Thm. 5.4.3] and [Reference Scholze22, Thm. 6.5], we have that
$\displaystyle \lim _{\leftarrow \ i} \vert U_i\vert $
). Moreover, by [Reference Diao, Lan, Liu and Zhu15, Thm. 5.4.3] and [Reference Scholze22, Thm. 6.5], we have that
 $$ \begin{align*} \widehat{{\cal O}}_{\mathcal{X}_{\mathrm{pke}}}^+(U)&=R^+,\quad \widehat{{\cal O}}_{\mathcal{X}_{\mathrm{pke}}}(U)=R, \quad \widehat{{\cal O}}_{\mathcal{X}^{\flat}_{\mathrm{pke}}}^+(U)=R^{\flat+}, \\ \widehat{{\cal O}}_{\mathcal{X}^{\flat}_{\mathrm{pke}}}(U)&=R^{\flat}, \quad \mathbb{A}_{\mathrm{inf}}(U)=W\bigl(R^{\flat+}\bigr) \end{align*} $$
$$ \begin{align*} \widehat{{\cal O}}_{\mathcal{X}_{\mathrm{pke}}}^+(U)&=R^+,\quad \widehat{{\cal O}}_{\mathcal{X}_{\mathrm{pke}}}(U)=R, \quad \widehat{{\cal O}}_{\mathcal{X}^{\flat}_{\mathrm{pke}}}^+(U)=R^{\flat+}, \\ \widehat{{\cal O}}_{\mathcal{X}^{\flat}_{\mathrm{pke}}}(U)&=R^{\flat}, \quad \mathbb{A}_{\mathrm{inf}}(U)=W\bigl(R^{\flat+}\bigr) \end{align*} $$
and the cohomology groups
(where
![]() $\sim $
means almost
$\sim $
means almost
![]() $0$
).
$0$
).
Thanks to [Reference Diao, Lan, Liu and Zhu15, Prop. 5.3.12 & Prop. 5.3.13], there exists a basis
![]() $\mathcal {B}$
for the site
$\mathcal {B}$
for the site
![]() $\mathcal {X}_{\mathrm {pke}}$
given by log affinoid perfectoid objects such that for every locally constant p-torsion sheaf
$\mathcal {X}_{\mathrm {pke}}$
given by log affinoid perfectoid objects such that for every locally constant p-torsion sheaf
![]() $\mathbb {L}$
on
$\mathbb {L}$
on
![]() $\mathcal {X}_{\mathrm {ket}}$
and every
$\mathcal {X}_{\mathrm {ket}}$
and every
![]() $U\in \mathcal {B}$
we have
$U\in \mathcal {B}$
we have
![]() $\mathrm {H}^i\bigl ( \mathcal {X}_{{\mathrm {pke}}}\vert _U,\mathbb {L}\bigr )=0$
for
$\mathrm {H}^i\bigl ( \mathcal {X}_{{\mathrm {pke}}}\vert _U,\mathbb {L}\bigr )=0$
for
![]() $i\geq 1$
. In case X is a fs log scheme over
$i\geq 1$
. In case X is a fs log scheme over
![]() ${\mathbb Q}_p$
, there is an analogous notion of log affinoid perfectoid opens of
${\mathbb Q}_p$
, there is an analogous notion of log affinoid perfectoid opens of
![]() $X_{\mathrm {pke}}$
, and it follows from the arguments in loc. cit. that there exists a basis of
$X_{\mathrm {pke}}$
, and it follows from the arguments in loc. cit. that there exists a basis of
![]() $X_{\mathrm {pke}}$
with the same property.
$X_{\mathrm {pke}}$
with the same property.
We recall that K was defined in the previous section as a perfectoid field of characteristic
![]() $0$
with an open and bounded subring
$0$
with an open and bounded subring
![]() $K^+$
. Assume that
$K^+$
. Assume that
![]() $\mathcal {X}$
is defined over
$\mathcal {X}$
is defined over
![]() $\mathrm {Spa}(K,K^+)$
. In this case,
$\mathrm {Spa}(K,K^+)$
. In this case,
![]() $\mathbb {A}_{\mathrm {inf}}$
, resp.
$\mathbb {A}_{\mathrm {inf}}$
, resp.
![]() $\widehat {{\cal O}}_{\mathcal {X}}^+$
, is a sheaf of algebras over the classical period ring
$\widehat {{\cal O}}_{\mathcal {X}}^+$
, is a sheaf of algebras over the classical period ring
![]() $\mathrm {A}_{\mathrm {inf}}:=\mathrm {W}\bigl (K^{\flat +}\bigr )$
, resp. over
$\mathrm {A}_{\mathrm {inf}}:=\mathrm {W}\bigl (K^{\flat +}\bigr )$
, resp. over
![]() $K^+$
, and given a generator
$K^+$
, and given a generator
![]() $\zeta \in \mathrm {A}_{\mathrm {inf}}$
for the kernel of the canonical ring homomorphism
$\zeta \in \mathrm {A}_{\mathrm {inf}}$
for the kernel of the canonical ring homomorphism
![]() $\mathrm {A}_{\mathrm {inf}}\to K^+$
, it follows from [Reference Scholze22, Lemma 6.3] that we have an exact sequence
$\mathrm {A}_{\mathrm {inf}}\to K^+$
, it follows from [Reference Scholze22, Lemma 6.3] that we have an exact sequence
2.4 Comparison results
Assume that
![]() $\mathcal {X}$
is a finite saturated locally noetherian log adic space over a perfectoid field
$\mathcal {X}$
is a finite saturated locally noetherian log adic space over a perfectoid field
![]() $\mathrm {Spa}(K,K^+)$
with K algebraically closed of characteristic
$\mathrm {Spa}(K,K^+)$
with K algebraically closed of characteristic
![]() $0$
. Firstly, the main result of [Reference Diao, Lan, Liu and Zhu15], namely Theorem 6.2.1, states that if the underlying adic space to
$0$
. Firstly, the main result of [Reference Diao, Lan, Liu and Zhu15], namely Theorem 6.2.1, states that if the underlying adic space to
![]() $\mathcal {X}$
is log smooth and proper and
$\mathcal {X}$
is log smooth and proper and
![]() $\mathbb {L}$
is an
$\mathbb {L}$
is an
![]() $\mathbb {F}_p$
-local system on
$\mathbb {F}_p$
-local system on
![]() $\mathcal {X}_{\mathrm {ket}}$
, then the cohomology groups
$\mathcal {X}_{\mathrm {ket}}$
, then the cohomology groups
![]() $\mathrm {H}^i(\mathcal {X}_{\mathrm {ket}},\mathbb {L}\big )$
are finite for all i, they vanish for
$\mathrm {H}^i(\mathcal {X}_{\mathrm {ket}},\mathbb {L}\big )$
are finite for all i, they vanish for
![]() $i\gg 0$
and the natural map
$i\gg 0$
and the natural map
is an almost isomorphism for every
![]() $i\geq 0$
. As
$i\geq 0$
. As
![]() ${\cal F}\cong \mathrm {R}\nu _{\ast }\nu ^{-1}\bigl ({\cal F}\bigr )$
for any sheaf of abelian goups, we obtain the same cohomology groups replacing
${\cal F}\cong \mathrm {R}\nu _{\ast }\nu ^{-1}\bigl ({\cal F}\bigr )$
for any sheaf of abelian goups, we obtain the same cohomology groups replacing
![]() $\mathcal {X}_{\mathrm {ket}}$
with
$\mathcal {X}_{\mathrm {ket}}$
with
![]() $\mathcal {X}_{\mathrm {pke}}$
in the isomorphisms above. Here, we denoted
$\mathcal {X}_{\mathrm {pke}}$
in the isomorphisms above. Here, we denoted
![]() $\nu \colon \mathcal {X}_{\mathrm {pke}}\longrightarrow \mathcal {X}_{\mathrm {ket}}$
the natural morphism of sites.
$\nu \colon \mathcal {X}_{\mathrm {pke}}\longrightarrow \mathcal {X}_{\mathrm {ket}}$
the natural morphism of sites.
Second, in the case X is finite separated locally noetherian log scheme, proper and log smooth over K, we have a géométrie algébrique et géométrie analytique (GAGA) type comparison isomorphism. Let
![]() $\mathcal {X}$
be the associated log adic space over
$\mathcal {X}$
be the associated log adic space over
![]() $\mathrm {Spa}(K,K^+)$
. We have a natural morphism of sites
$\mathrm {Spa}(K,K^+)$
. We have a natural morphism of sites
![]() $\gamma \colon \mathcal {X}_{\mathrm {ket}} \to X_{\mathrm {ket}}$
. Let
$\gamma \colon \mathcal {X}_{\mathrm {ket}} \to X_{\mathrm {ket}}$
. Let
![]() $\mathbb {L}$
be an
$\mathbb {L}$
be an
![]() $\mathbb {F}_p$
-local system on
$\mathbb {F}_p$
-local system on
![]() $X_{\mathrm {ket}}$
. Then
$X_{\mathrm {ket}}$
. Then
Proposition 2.1. For every
![]() $i\geq 0$
the natural morphism
$i\geq 0$
the natural morphism
![]() $\mathrm {H}^i(X_{\mathrm {ket}},\mathbb {L}\big ) \longrightarrow \mathrm {H}^i(\mathcal {X}_{\mathrm {ket}},\gamma ^{\ast }\bigl (\mathbb {L}\bigr )\big )$
is an isomorphism.
$\mathrm {H}^i(X_{\mathrm {ket}},\mathbb {L}\big ) \longrightarrow \mathrm {H}^i(\mathcal {X}_{\mathrm {ket}},\gamma ^{\ast }\bigl (\mathbb {L}\bigr )\big )$
is an isomorphism.
Proof. Let
![]() $X^o$
and
$X^o$
and
![]() $\mathcal {X}^o$
be the scheme, resp. the adic space defined by X and
$\mathcal {X}^o$
be the scheme, resp. the adic space defined by X and
![]() $\mathcal {X}$
forgetting the log structures. In this case, the morphism of sites
$\mathcal {X}$
forgetting the log structures. In this case, the morphism of sites
![]() $\gamma ^o\colon \mathcal {X}_{\mathrm {et}}^o \to X_{\mathrm {et}}^o$
induces the map
$\gamma ^o\colon \mathcal {X}_{\mathrm {et}}^o \to X_{\mathrm {et}}^o$
induces the map
![]() $\mathrm {H}^i(X_{\mathrm {et}}^o,F\big ) \longrightarrow \mathrm {H}^i(\mathcal {X}_{\mathrm {et}}^o,\gamma ^{o,\ast }\bigl (F\bigr )\big )$
for every sheaf of torsion abelian groups F. It is an isomorphism due to [Reference Huber17, Thm. 3.2.10]. Consider the commutative diagram of sites
$\mathrm {H}^i(X_{\mathrm {et}}^o,F\big ) \longrightarrow \mathrm {H}^i(\mathcal {X}_{\mathrm {et}}^o,\gamma ^{o,\ast }\bigl (F\bigr )\big )$
for every sheaf of torsion abelian groups F. It is an isomorphism due to [Reference Huber17, Thm. 3.2.10]. Consider the commutative diagram of sites
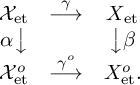 $$ \begin{align*}\begin{array}{ccc} \mathcal{X}_{\mathrm{et}} & \stackrel{\gamma}{\longrightarrow} & X_{\mathrm{et}} \cr \alpha \big\downarrow & & \big\downarrow \beta \cr \mathcal{X}_{\mathrm{et}}^o & \stackrel {\gamma^o}{\longrightarrow} & X_{\mathrm{et}}^o. \cr \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccc} \mathcal{X}_{\mathrm{et}} & \stackrel{\gamma}{\longrightarrow} & X_{\mathrm{et}} \cr \alpha \big\downarrow & & \big\downarrow \beta \cr \mathcal{X}_{\mathrm{et}}^o & \stackrel {\gamma^o}{\longrightarrow} & X_{\mathrm{et}}^o. \cr \end{array} \end{align*} $$
Using the compatibility of the Leray spectral sequences
![]() $\mathrm {H}^i(\mathcal {X}_{\mathrm {et}}^o,\mathrm {R}^j \alpha _{\ast } \gamma ^{\ast }(\mathbb {L})\big ) \Longrightarrow \mathrm {H}^{i+j}(\mathcal {X}_{\mathrm {ket}},\gamma ^{\ast }\bigl (\mathbb {L}\bigr )\big )$
and
$\mathrm {H}^i(\mathcal {X}_{\mathrm {et}}^o,\mathrm {R}^j \alpha _{\ast } \gamma ^{\ast }(\mathbb {L})\big ) \Longrightarrow \mathrm {H}^{i+j}(\mathcal {X}_{\mathrm {ket}},\gamma ^{\ast }\bigl (\mathbb {L}\bigr )\big )$
and
![]() $\mathrm {H}^i(X_{\mathrm {et}}^o,\mathrm {R}^j \beta _{\ast } (\mathbb {L})\big ) \Longrightarrow \mathrm {H}^{i+j}(X_{\mathrm {ket}},\mathbb {L}\big )$
and the result of Huber, it suffices to prove that the natural morphism
$\mathrm {H}^i(X_{\mathrm {et}}^o,\mathrm {R}^j \beta _{\ast } (\mathbb {L})\big ) \Longrightarrow \mathrm {H}^{i+j}(X_{\mathrm {ket}},\mathbb {L}\big )$
and the result of Huber, it suffices to prove that the natural morphism
is an isomorphism of sheaves for every j. It suffices to prove that we get an isomorphism after passing to stalks at geometric points
![]() $\zeta =\mathrm {Spa}\bigl (l,l^+\bigr ) \to \mathcal {X}^o$
as those form a conservative family by [Reference Huber17, Prop. 2.5.5]. Recall that
$\zeta =\mathrm {Spa}\bigl (l,l^+\bigr ) \to \mathcal {X}^o$
as those form a conservative family by [Reference Huber17, Prop. 2.5.5]. Recall that
![]() $\zeta $
might consist of more than one point but it has a unique closed point
$\zeta $
might consist of more than one point but it has a unique closed point
![]() $\zeta _0$
. Taking the stalk at
$\zeta _0$
. Taking the stalk at
![]() $\zeta $
is equivalent to take global sections over the associated strictly local adic space
$\zeta $
is equivalent to take global sections over the associated strictly local adic space
![]() $\mathcal {X}^o(\zeta )$
(see [Reference Huber17, Lemma 2.5.12]). Let
$\mathcal {X}^o(\zeta )$
(see [Reference Huber17, Lemma 2.5.12]). Let
![]() $X^o(\zeta _0)$
be the spectrum of the strict Henselization of X at
$X^o(\zeta _0)$
be the spectrum of the strict Henselization of X at
![]() $\zeta _0$
. Taking the stalk at
$\zeta _0$
. Taking the stalk at
![]() $\zeta $
of
$\zeta $
of
![]() $\gamma ^{o,\ast }$
of a sheaf is equivalent to taking the sections of that sheaf over
$\gamma ^{o,\ast }$
of a sheaf is equivalent to taking the sections of that sheaf over
![]() $X^o(\zeta _0)$
. We have a natural map of sites
$X^o(\zeta _0)$
. We have a natural map of sites
![]() $\mathcal {X}^o(\zeta )_{\mathrm {ket}}\to X^o(\zeta _0)_{\mathrm {ket}}$
, considering on
$\mathcal {X}^o(\zeta )_{\mathrm {ket}}\to X^o(\zeta _0)_{\mathrm {ket}}$
, considering on
![]() $X^o(\zeta )$
and on
$X^o(\zeta )$
and on
![]() $ \mathcal {X}^o(\zeta )$
the log structures coming from X and
$ \mathcal {X}^o(\zeta )$
the log structures coming from X and
![]() $\mathcal {X}$
. We need to show that it is an equivalence. In both cases, the Kummer étale sites are the same as the finite Kummer étale sites; indeed by definition the Kummer étale topology is generated in both cases by finite Kummer étale covers and classical étale morphisms and a Kummer cover of
$\mathcal {X}$
. We need to show that it is an equivalence. In both cases, the Kummer étale sites are the same as the finite Kummer étale sites; indeed by definition the Kummer étale topology is generated in both cases by finite Kummer étale covers and classical étale morphisms and a Kummer cover of
![]() $X^o(\zeta )$
, resp.
$X^o(\zeta )$
, resp.
![]() $ \mathcal {X}^o(\zeta )$
, is still strictly local and hence does not admit any nontrivial classical étale cover (see [Reference Huber17, Lemma 2.5.6] in the adic setting). Both in the schematic and in the adic setting, the finite Kummer étale sites are equivalent to the category of finite sets with continuous action of the group
$ \mathcal {X}^o(\zeta )$
, is still strictly local and hence does not admit any nontrivial classical étale cover (see [Reference Huber17, Lemma 2.5.6] in the adic setting). Both in the schematic and in the adic setting, the finite Kummer étale sites are equivalent to the category of finite sets with continuous action of the group
![]() $\mathrm {Hom}(\overline {M}^{\mathrm {gp}},\widehat {{\mathbb Z}}\big )$
with
$\mathrm {Hom}(\overline {M}^{\mathrm {gp}},\widehat {{\mathbb Z}}\big )$
with
![]() $\overline {M}$
the stalk of the log structure at
$\overline {M}$
the stalk of the log structure at
![]() $\zeta $
, modulo
$\zeta $
, modulo
![]() $l^{\ast }$
. See [Reference Illusie18, Ex. 4.7(a)] in the schematic case and [Reference Diao, Lan, Liu and Zhu15, Prop. 4.4.7] in the adic case. As such quotient is the same in the schematic and adic cases, the conclusion follows.
$l^{\ast }$
. See [Reference Illusie18, Ex. 4.7(a)] in the schematic case and [Reference Diao, Lan, Liu and Zhu15, Prop. 4.4.7] in the adic case. As such quotient is the same in the schematic and adic cases, the conclusion follows.
3 VBMS and dual VBMS
3.1 VBMS, that is, vector bundles with marked sections
We recall the main constructions of [Reference Andreatta and Iovita2] and [Reference Andreatta, Iovita and Pilloni4]. Let
![]() $\mathcal {X}$
denote an adic analytic space over
$\mathcal {X}$
denote an adic analytic space over
![]() $\mathrm {Spa}({\mathbb Q}_p, {\mathbb Z}_p)$
and let
$\mathrm {Spa}({\mathbb Q}_p, {\mathbb Z}_p)$
and let
![]() $({\cal E}, {\cal E}^+)$
denote a pair consisting of a locally free
$({\cal E}, {\cal E}^+)$
denote a pair consisting of a locally free
![]() ${\cal O}_{\mathcal {X}}$
-module
${\cal O}_{\mathcal {X}}$
-module
![]() ${\cal E}$
of rank
${\cal E}$
of rank
![]() $2$
and a subsheaf
$2$
and a subsheaf
![]() ${\cal E}^+$
of
${\cal E}^+$
of
![]() ${\cal E}$
which is a locally free
${\cal E}$
which is a locally free
![]() ${\cal O}_{\mathcal {X}}^+$
-module of rank
${\cal O}_{\mathcal {X}}^+$
-module of rank
![]() $2$
such that
$2$
such that
![]() ${\cal E}={\cal E}^+\otimes _{{\cal O}_{\mathcal {X}}^+}{\cal O}_{\mathcal {X}}$
. Let
${\cal E}={\cal E}^+\otimes _{{\cal O}_{\mathcal {X}}^+}{\cal O}_{\mathcal {X}}$
. Let
![]() ${\cal I}\subset {\cal O}_{\mathcal {X}}^+$
be an invertible ideal such that
${\cal I}\subset {\cal O}_{\mathcal {X}}^+$
be an invertible ideal such that
![]() ${\cal I}$
gives the topology on
${\cal I}$
gives the topology on
![]() ${\cal O}_{\mathcal {X}}^+$
, and let
${\cal O}_{\mathcal {X}}^+$
, and let
![]() $r\ge 0$
be an integer such that
$r\ge 0$
be an integer such that
![]() $ {\cal I} \subset p^r {\cal O}_{\mathcal {X}}^+$
.
$ {\cal I} \subset p^r {\cal O}_{\mathcal {X}}^+$
.
We suppose that there is a section
![]() $s\in \mathrm {H}^0(\mathcal {X}, {\cal E}^+/{\cal I}{\cal E}^+)$
such that the submodule
$s\in \mathrm {H}^0(\mathcal {X}, {\cal E}^+/{\cal I}{\cal E}^+)$
such that the submodule
![]() $\bigl ({\cal O}_{\mathcal {X}}^+/{\cal I}\bigr ) s$
is a direct summand of
$\bigl ({\cal O}_{\mathcal {X}}^+/{\cal I}\bigr ) s$
is a direct summand of
![]() ${\cal E}^+/{\cal I}{\cal E}^+$
. We have the following.
${\cal E}^+/{\cal I}{\cal E}^+$
. We have the following.
Theorem 3.1 [Reference Andreatta, Iovita and Pilloni4].
a) The functor attaching to every adic space
![]() $\gamma \colon {\cal Z}\rightarrow \mathcal {X}$
such that
$\gamma \colon {\cal Z}\rightarrow \mathcal {X}$
such that
![]() $t^{\ast }({\cal I})$
is an invertible ideal in
$t^{\ast }({\cal I})$
is an invertible ideal in
![]() ${\cal O}_{{\cal Z}}^+$
, the set (group in fact):
${\cal O}_{{\cal Z}}^+$
, the set (group in fact):
is represented by the adic vector bundle
![]() ${\mathbb V}({\cal E},{\cal E}^+):=\mathrm {Spa}_{\mathcal {X}}\bigl (\mathrm {Sym}({\cal E}), \mathrm {Sym}({\cal E}^+) \bigr )\rightarrow \mathcal {X}$
.
${\mathbb V}({\cal E},{\cal E}^+):=\mathrm {Spa}_{\mathcal {X}}\bigl (\mathrm {Sym}({\cal E}), \mathrm {Sym}({\cal E}^+) \bigr )\rightarrow \mathcal {X}$
.
b) The subfunctor of
![]() ${\mathbb V}({\cal E}, {\cal E}^+)$
denoted
${\mathbb V}({\cal E}, {\cal E}^+)$
denoted
![]() ${\mathbb V}_0({\cal E}^+, s)$
which associates to every adic space
${\mathbb V}_0({\cal E}^+, s)$
which associates to every adic space
![]() $\gamma \colon {\cal Z}\rightarrow \mathcal {X}$
as above, the set:
$\gamma \colon {\cal Z}\rightarrow \mathcal {X}$
as above, the set:
is represented by the open adic subspace of
![]() ${\mathbb V}({\cal E},{\cal E}^+)$
, also denoted
${\mathbb V}({\cal E},{\cal E}^+)$
, also denoted
![]() ${\mathbb V}_0({\cal E}^+,s)$
, consisting of the points x such that
${\mathbb V}_0({\cal E}^+,s)$
, consisting of the points x such that
![]() $\vert \tilde {s}-1\vert _x\le \vert \alpha \vert _x$
, where
$\vert \tilde {s}-1\vert _x\le \vert \alpha \vert _x$
, where
![]() $\tilde {s}$
is a (local) lift of s to
$\tilde {s}$
is a (local) lift of s to
![]() ${\cal E}^+$
and
${\cal E}^+$
and
![]() $\alpha $
is a (local) generator of
$\alpha $
is a (local) generator of
![]() ${\cal I}$
at x.
${\cal I}$
at x.
c) Suppose that we have sections s and
![]() $t\in \mathrm {H}^0(\mathcal {X}, {\cal E}^+/{\cal I}{\cal E}^+)$
which form an
$t\in \mathrm {H}^0(\mathcal {X}, {\cal E}^+/{\cal I}{\cal E}^+)$
which form an
![]() $\bigl ({\cal O}_{\mathcal {X}}^+/{\cal I}\bigr )$
-basis of
$\bigl ({\cal O}_{\mathcal {X}}^+/{\cal I}\bigr )$
-basis of
![]() ${\cal E}^+/{\cal I}{\cal E}^+$
. Then, the subfunctor
${\cal E}^+/{\cal I}{\cal E}^+$
. Then, the subfunctor
![]() ${\mathbb V}_0({\cal E}^+,s,t)$
of
${\mathbb V}_0({\cal E}^+,s,t)$
of
![]() ${\mathbb V}_0({\cal E}^+, s)$
which associates to every adic space
${\mathbb V}_0({\cal E}^+, s)$
which associates to every adic space
![]() $\gamma \colon {\cal Z}\rightarrow \mathcal {X}$
, the set:
$\gamma \colon {\cal Z}\rightarrow \mathcal {X}$
, the set:
is represented by the open adic subspace
![]() ${\mathbb V}_0({\cal E}^+,s, t)$
of
${\mathbb V}_0({\cal E}^+,s, t)$
of
![]() ${\mathbb V}_0({\cal E}^+, s)$
consisting of the points x such that
${\mathbb V}_0({\cal E}^+, s)$
consisting of the points x such that
![]() $\vert \tilde {t}\vert _x\le \vert \alpha \vert _x$
for a (any) lift
$\vert \tilde {t}\vert _x\le \vert \alpha \vert _x$
for a (any) lift
![]() $\tilde {t}$
of t to
$\tilde {t}$
of t to
![]() ${\cal E}^+$
and
${\cal E}^+$
and
![]() $\alpha $
a (local) generator of
$\alpha $
a (local) generator of
![]() ${\cal I}$
at x.
${\cal I}$
at x.
Proof. The proof is local on
![]() $\mathcal {X}$
. Assume that
$\mathcal {X}$
. Assume that
![]() $U\subset \mathcal {X}$
is an affinoid open
$U\subset \mathcal {X}$
is an affinoid open
![]() $U=\mathrm {Spa}(R,R^+)$
such that
$U=\mathrm {Spa}(R,R^+)$
such that
![]() ${\cal I}\vert _U$
is principal generated by
${\cal I}\vert _U$
is principal generated by
![]() $\alpha \in R^+$
and
$\alpha \in R^+$
and
![]() ${\cal E}^+\vert _U$
is free with basis
${\cal E}^+\vert _U$
is free with basis
![]() $f_0$
,
$f_0$
,
![]() $f_1$
with
$f_1$
with
![]() $f_0(\mathrm {mod}\ \alpha )=s\vert _U$
. Then
$f_0(\mathrm {mod}\ \alpha )=s\vert _U$
. Then
![]() $f_1(\mathrm {mod}\ \alpha ) $
generates
$f_1(\mathrm {mod}\ \alpha ) $
generates
![]() $\Bigl (\bigl ({\cal E}^+/{\cal I}{\cal E}^+\bigr )/s\bigl ({\cal O}_{\mathcal {X}}^+/{\cal I} \bigr )\Bigr )\vert _U$
and we assume in case (c) that
$\Bigl (\bigl ({\cal E}^+/{\cal I}{\cal E}^+\bigr )/s\bigl ({\cal O}_{\mathcal {X}}^+/{\cal I} \bigr )\Bigr )\vert _U$
and we assume in case (c) that
![]() $f_1(\mathrm {mod}\ \alpha )=t\vert _U$
. Then by [Reference Andreatta and Iovita2, §2] we have
$f_1(\mathrm {mod}\ \alpha )=t\vert _U$
. Then by [Reference Andreatta and Iovita2, §2] we have
![]() ${\mathbb V}({\cal E},{\cal E}^+)\vert _U=\mathrm {Spa}\bigl (R\langle X,Y\rangle , R^+\langle X,Y\rangle \bigr )$
and
${\mathbb V}({\cal E},{\cal E}^+)\vert _U=\mathrm {Spa}\bigl (R\langle X,Y\rangle , R^+\langle X,Y\rangle \bigr )$
and
where
![]() $\displaystyle X=1+\alpha Z$
giving also the map to
$\displaystyle X=1+\alpha Z$
giving also the map to
![]() ${\mathbb V}({\cal E},{\cal E}^+)\vert _U$
. Similarly,
${\mathbb V}({\cal E},{\cal E}^+)\vert _U$
. Similarly,
with
![]() $\displaystyle Y=\alpha W$
. We have the tautological map over
$\displaystyle Y=\alpha W$
. We have the tautological map over
![]() ${\mathbb V}({\cal E},{\cal E}^+)\vert _U$
given by
${\mathbb V}({\cal E},{\cal E}^+)\vert _U$
given by
from which we deduce similarly the tautological maps over
![]() ${\mathbb V}_0({\cal E}^+,s)\vert _U$
and
${\mathbb V}_0({\cal E}^+,s)\vert _U$
and
![]() ${\mathbb V}_0({\cal E}^+,s,t)\vert _U$
providing the claimed representability and concluding the proof.
${\mathbb V}_0({\cal E}^+,s,t)\vert _U$
providing the claimed representability and concluding the proof.
3.2 Dual VBMS
In this article, we’ll need a variant of the construction in Section §3.1 which we now present. Suppose that
![]() $\mathcal {X}$
,
$\mathcal {X}$
,
![]() ${\cal I}$
,
${\cal I}$
,
![]() $({\cal E}, {\cal E}^+)$
are as in Section §3.1. Moreover, we assume that there is an exact sequence of locally free
$({\cal E}, {\cal E}^+)$
are as in Section §3.1. Moreover, we assume that there is an exact sequence of locally free
![]() ${\cal O}_{\mathcal {X}}^+/{\cal I}$
-modules
${\cal O}_{\mathcal {X}}^+/{\cal I}$
-modules
and a section
![]() $s\in \mathrm {H}^0\bigl (\mathcal {X}, {\cal F} \bigr )$
such that
$s\in \mathrm {H}^0\bigl (\mathcal {X}, {\cal F} \bigr )$
such that
![]() $\bigl ({\cal O}_{\mathcal {X}}^+/{\cal I} \bigr )s={\cal F}$
. We have:
$\bigl ({\cal O}_{\mathcal {X}}^+/{\cal I} \bigr )s={\cal F}$
. We have:
Theorem 3.2. The subfunctor
![]() ${\mathbb V}_0^D({\cal E}^+, \mathcal {Q}, s)$
of
${\mathbb V}_0^D({\cal E}^+, \mathcal {Q}, s)$
of
![]() ${\mathbb V}({\cal E},{\cal E}^+)$
, defined by associating to every adic space
${\mathbb V}({\cal E},{\cal E}^+)$
, defined by associating to every adic space
![]() $t\colon {\cal Z}\rightarrow \mathcal {X}$
as in Section §3.1 the set
$t\colon {\cal Z}\rightarrow \mathcal {X}$
as in Section §3.1 the set
is represented by the the open adic subspace of
![]() ${\mathbb V}({\cal E}, {\cal E}^+)$
denoted
${\mathbb V}({\cal E}, {\cal E}^+)$
denoted
![]() ${\mathbb V}_0^D({\cal E}^+, \mathcal {Q},s)$
and consisting of the points x such that
${\mathbb V}_0^D({\cal E}^+, \mathcal {Q},s)$
and consisting of the points x such that
![]() $\vert q\vert _x\le \vert \alpha \vert _x$
and
$\vert q\vert _x\le \vert \alpha \vert _x$
and
![]() $\vert \tilde {s}-1\vert _x\le \vert \alpha \vert _x$
, where q is a (local) lift to
$\vert \tilde {s}-1\vert _x\le \vert \alpha \vert _x$
, where q is a (local) lift to
![]() ${\cal E}^+$
of a local generator of
${\cal E}^+$
of a local generator of
![]() $\mathcal {Q}$
at x,
$\mathcal {Q}$
at x,
![]() $\alpha $
is a (local) generator of
$\alpha $
is a (local) generator of
![]() ${\cal I}$
at x and
${\cal I}$
at x and
![]() $\tilde {s}$
is a (local) lift of s to
$\tilde {s}$
is a (local) lift of s to
![]() ${\cal E}^+$
.
${\cal E}^+$
.
3.3 The sheaves
 ${\mathbb W}_k$
and
${\mathbb W}_k$
and
 ${\mathbb W}^D_k$
${\mathbb W}^D_k$
Let the hypothesis be as in Section §3.1 and §3.2. We assume that we have a morphism of adic spaces
![]() $\mathcal {X}\to {\cal W}$
where let us recall that
$\mathcal {X}\to {\cal W}$
where let us recall that
![]() ${\cal W}$
is the adic weight space for
${\cal W}$
is the adic weight space for
![]() $\mathrm {\mathbf {GL}}_{2,/{\mathbb Q}}$
. For every adic space
$\mathrm {\mathbf {GL}}_{2,/{\mathbb Q}}$
. For every adic space
![]() ${\cal Z}$
, the morphisms
${\cal Z}$
, the morphisms
![]() ${\cal Z}\to {\cal W}$
classify continuous homomorphisms
${\cal Z}\to {\cal W}$
classify continuous homomorphisms
![]() ${\mathbb Z}_p^{\ast } \to \Gamma \bigl ({\cal Z},{\cal O}_{{\cal Z}}\bigr )$
. We denote by
${\mathbb Z}_p^{\ast } \to \Gamma \bigl ({\cal Z},{\cal O}_{{\cal Z}}\bigr )$
. We denote by
![]() $k^{\mathrm {univ}}\colon {\mathbb Z}_p^{\ast } \to \Gamma \bigl (\mathcal {X},{\cal O}_{\mathcal {X}}\bigr )$
the continuous homomorphism defined by
$k^{\mathrm {univ}}\colon {\mathbb Z}_p^{\ast } \to \Gamma \bigl (\mathcal {X},{\cal O}_{\mathcal {X}}\bigr )$
the continuous homomorphism defined by
![]() $\mathcal {X}\to {\cal W}$
. We assume that
$\mathcal {X}\to {\cal W}$
. We assume that
![]() $k^{\mathrm {univ}}$
satisfies the following analyticity assumption: There exists a section
$k^{\mathrm {univ}}$
satisfies the following analyticity assumption: There exists a section
![]() $u_{\mathrm {univ}}$
of
$u_{\mathrm {univ}}$
of
![]() ${\cal O}_{\mathcal {X}}$
such that
${\cal O}_{\mathcal {X}}$
such that
![]() $\vert u_{\mathrm {univ}} \vert _x < \vert p^{\frac {1}{p-1} -r} \vert _x$
for every
$\vert u_{\mathrm {univ}} \vert _x < \vert p^{\frac {1}{p-1} -r} \vert _x$
for every
![]() $x\in \mathcal {X}$
and
$x\in \mathcal {X}$
and
We recall that the integer
![]() $r\ge 0$
is such that
$r\ge 0$
is such that
![]() ${\cal I}\subset p^r {\cal O}_{\mathcal {X}}^+$
. Let us denote by
${\cal I}\subset p^r {\cal O}_{\mathcal {X}}^+$
. Let us denote by
![]() ${\cal T}$
the adic torus representing the functor which associates to an adic space
${\cal T}$
the adic torus representing the functor which associates to an adic space
![]() $\gamma \colon {\cal Z}\rightarrow \mathcal {X}$
the group
$\gamma \colon {\cal Z}\rightarrow \mathcal {X}$
the group
Then
![]() $k^{\mathrm {univ}}$
defines a character
$k^{\mathrm {univ}}$
defines a character
![]() $k^{\mathrm {univ}}\colon {\cal T} \to \mathbb {G}_m$
, that is, a morphism of adic spaces and group functors, using the fomula above.
$k^{\mathrm {univ}}\colon {\cal T} \to \mathbb {G}_m$
, that is, a morphism of adic spaces and group functors, using the fomula above.
We have natural actions of
![]() ${\cal T}$
on
${\cal T}$
on
![]() ${\mathbb V}_0({\cal E}^+, s)$
,
${\mathbb V}_0({\cal E}^+, s)$
,
![]() ${\mathbb V}_0({\cal E}^+, s,t)$
and
${\mathbb V}_0({\cal E}^+, s,t)$
and
![]() ${\mathbb V}_0^D\bigl ({\cal E}^+,\mathcal {Q}, s \bigr )$
defined on
${\mathbb V}_0^D\bigl ({\cal E}^+,\mathcal {Q}, s \bigr )$
defined on
![]() $\gamma \colon {\cal Z}\rightarrow \mathcal {X}$
points by:
$\gamma \colon {\cal Z}\rightarrow \mathcal {X}$
points by:
![]() $u\ast h:=uh$
and
$u\ast h:=uh$
and
![]() $u\ast h':=uh'$
, where
$u\ast h':=uh'$
, where
![]() $u\in {\cal T}(\gamma \colon {\cal Z}\rightarrow \mathcal {X})$
,
$u\in {\cal T}(\gamma \colon {\cal Z}\rightarrow \mathcal {X})$
,
![]() $h\in {\mathbb V}_0({\cal E}^+, s)(\gamma \colon {\cal Z}\rightarrow \mathcal {X})$
, resp.
$h\in {\mathbb V}_0({\cal E}^+, s)(\gamma \colon {\cal Z}\rightarrow \mathcal {X})$
, resp.
![]() $h\in {\mathbb V}_0({\cal E}^+, s,t)(\gamma \colon {\cal Z}\rightarrow \mathcal {X})$
, resp.
$h\in {\mathbb V}_0({\cal E}^+, s,t)(\gamma \colon {\cal Z}\rightarrow \mathcal {X})$
, resp.
![]() $h'\in {\mathbb V}_0^D\bigl ( {\cal E}^+,\mathcal {Q}, s\bigr )(\gamma \colon {\cal Z}\rightarrow \mathcal {X})$
. Let us denote by
$h'\in {\mathbb V}_0^D\bigl ( {\cal E}^+,\mathcal {Q}, s\bigr )(\gamma \colon {\cal Z}\rightarrow \mathcal {X})$
. Let us denote by
![]() $f\colon {\mathbb V}_0({\cal E}^+,s)\longrightarrow \mathcal {X}$
,
$f\colon {\mathbb V}_0({\cal E}^+,s)\longrightarrow \mathcal {X}$
,
![]() $g\colon {\mathbb V}_0({\cal E}^+,s,t)\longrightarrow \mathcal {X}$
and by
$g\colon {\mathbb V}_0({\cal E}^+,s,t)\longrightarrow \mathcal {X}$
and by
![]() $f^D:{\mathbb V}_0^D\bigl ({\cal E}^+,\mathcal {Q}, s\bigr )\longrightarrow \mathcal {X}$
the structural morphisms.
$f^D:{\mathbb V}_0^D\bigl ({\cal E}^+,\mathcal {Q}, s\bigr )\longrightarrow \mathcal {X}$
the structural morphisms.
Definition 3.3. We denote
and
where if
![]() ${\cal G}$
is an
${\cal G}$
is an
![]() ${\cal O}_{\mathcal {X}}^+$
-module on
${\cal O}_{\mathcal {X}}^+$
-module on
![]() $\mathcal {X}$
with an action by the torus
$\mathcal {X}$
with an action by the torus
![]() ${\cal T}:=1+{\cal I}$
, we denote
${\cal T}:=1+{\cal I}$
, we denote
![]() ${\cal G}[k^{\mathrm {univ}}]$
the subsheaf of
${\cal G}[k^{\mathrm {univ}}]$
the subsheaf of
![]() ${\cal G}$
of sections x such that
${\cal G}$
of sections x such that
![]() $u\ast x=k^{\mathrm {univ}}(u)x$
for all corresponding sections u of
$u\ast x=k^{\mathrm {univ}}(u)x$
for all corresponding sections u of
![]() ${\cal T}$
.
${\cal T}$
.
3.3.1 Local descriptions of the sheaves
 ${\mathbb W}_k$
and
${\mathbb W}_k$
and
 ${\mathbb W}_k^D$
${\mathbb W}_k^D$
We assume all notations and assumptions of the proof of Theorem 3.1 and of Section §3.3. Let
![]() $U=\mathrm {Spa}(R,R^+)\subset \mathcal {X}$
be an affinoid open such that
$U=\mathrm {Spa}(R,R^+)\subset \mathcal {X}$
be an affinoid open such that
![]() ${\cal E}^+\vert _U=f_0{\cal O}_U^++f_1{\cal O}_U^+$
,
${\cal E}^+\vert _U=f_0{\cal O}_U^++f_1{\cal O}_U^+$
,
![]() ${\cal I}\vert _U=\alpha {\cal O}_U^+$
and such that
${\cal I}\vert _U=\alpha {\cal O}_U^+$
and such that
![]() $f_0(\mathrm {mod}\ \alpha )=s\vert _U$
and
$f_0(\mathrm {mod}\ \alpha )=s\vert _U$
and
![]() $f_1(\mathrm {mod}\ \alpha ) $
generates
$f_1(\mathrm {mod}\ \alpha ) $
generates
![]() $\Bigl (\bigl ({\cal E}^+/{\cal I}{\cal E}^+\bigr )/s\bigl ({\cal O}_{\mathcal {X}}^+/{\cal I} \bigr )\Bigr )\vert _U$
(respectively
$\Bigl (\bigl ({\cal E}^+/{\cal I}{\cal E}^+\bigr )/s\bigl ({\cal O}_{\mathcal {X}}^+/{\cal I} \bigr )\Bigr )\vert _U$
(respectively
![]() $f_1(\mathrm {mod}\ \alpha )=t\vert _U$
).
$f_1(\mathrm {mod}\ \alpha )=t\vert _U$
).
In view of the next section, we also consider the dual situation, that is, recall that s is a global marked section of
![]() ${\cal E}^+$
modulo
${\cal E}^+$
modulo
![]() ${\cal I}$
and denote
${\cal I}$
and denote
![]() ${\cal F}:=({\cal E}^+/{\cal I}{\cal E}^+)/\bigl (s({\cal O}_{\mathcal {X}}^+/{\cal I})\bigr )$
. By dualizing, we obtain the exact sequence
${\cal F}:=({\cal E}^+/{\cal I}{\cal E}^+)/\bigl (s({\cal O}_{\mathcal {X}}^+/{\cal I})\bigr )$
. By dualizing, we obtain the exact sequence
where
![]() $\mathcal {Q}:={\cal F}^{\vee }$
, which defines data for
$\mathcal {Q}:={\cal F}^{\vee }$
, which defines data for
![]() ${\mathbb V}_0^D$
. Then
${\mathbb V}_0^D$
. Then
![]() $({\cal E}^+)^{\vee }\vert _U=f_0^{\vee }{\cal O}_{U}^++ f_1^{\vee }{\cal O}_{U}^+$
,
$({\cal E}^+)^{\vee }\vert _U=f_0^{\vee }{\cal O}_{U}^++ f_1^{\vee }{\cal O}_{U}^+$
,
![]() $\mathcal {Q}\vert _U=f_1^{\vee }\bigl ({\cal O}_U^+/\alpha {\cal O}_U^+\bigr )$
and
$\mathcal {Q}\vert _U=f_1^{\vee }\bigl ({\cal O}_U^+/\alpha {\cal O}_U^+\bigr )$
and
![]() $f_0^{\vee }(\mathrm {mod}\ \alpha )=s^{\vee }\vert _U$
. Therefore, as in [Reference Andreatta and Iovita2, Lemma 2.4], one proves that
$f_0^{\vee }(\mathrm {mod}\ \alpha )=s^{\vee }\vert _U$
. Therefore, as in [Reference Andreatta and Iovita2, Lemma 2.4], one proves that
where
![]() $\displaystyle X=1+\alpha Z$
and
$\displaystyle X=1+\alpha Z$
and
with
![]() $Y=\alpha W$
. Similarly, we have
$Y=\alpha W$
. Similarly, we have
where
![]() $A=1+\alpha C$
and
$A=1+\alpha C$
and
![]() $B=\alpha D$
.
$B=\alpha D$
.
Therefore, we have
and
3.4 The duality
Suppose that
![]() $\mathcal {X}$
,
$\mathcal {X}$
,
![]() ${\cal I}$
,
${\cal I}$
,
![]() $ ({\cal E}, {\cal E}^+)$
, s are as in Section §3.1, and let us denote by
$ ({\cal E}, {\cal E}^+)$
, s are as in Section §3.1, and let us denote by
Let
![]() $\bigl ({\cal E}', ({\cal E}^+)^{\vee }\bigr )$
denote the pair where
$\bigl ({\cal E}', ({\cal E}^+)^{\vee }\bigr )$
denote the pair where
![]() $({\cal E}^+)^{\vee }$
is the
$({\cal E}^+)^{\vee }$
is the
![]() ${\cal O}_{\mathcal {X}}^+$
-dual of
${\cal O}_{\mathcal {X}}^+$
-dual of
![]() ${\cal E}^+$
and
${\cal E}^+$
and
![]() ${\cal E}':=({\cal E}^+)^{\vee }\otimes _{{\cal O}_{\mathcal {X}}^+}{\cal O}_{\mathcal {X}}$
. Moreover, let us consider
${\cal E}':=({\cal E}^+)^{\vee }\otimes _{{\cal O}_{\mathcal {X}}^+}{\cal O}_{\mathcal {X}}$
. Moreover, let us consider
![]() $\mathcal {Q}:=\mathrm {Ker}\bigl (({\cal E}^+/{\cal I}{\cal E}^+)^{\vee }\stackrel {\iota ^{\vee }}{\longrightarrow }{\cal F}^{\vee } \bigr )$
, where
$\mathcal {Q}:=\mathrm {Ker}\bigl (({\cal E}^+/{\cal I}{\cal E}^+)^{\vee }\stackrel {\iota ^{\vee }}{\longrightarrow }{\cal F}^{\vee } \bigr )$
, where
![]() ${\cal F}^{\vee }$
is the
${\cal F}^{\vee }$
is the
![]() ${\cal O}_{\mathcal {X}}^+/{\cal I}$
-dual of
${\cal O}_{\mathcal {X}}^+/{\cal I}$
-dual of
![]() ${\cal F}$
. As explained in Theorems 3.1 and 3.2, we have adic spaces
${\cal F}$
. As explained in Theorems 3.1 and 3.2, we have adic spaces
![]() ${\mathbb V}_0({\cal E}^+,s)$
and
${\mathbb V}_0({\cal E}^+,s)$
and
![]() ${\mathbb V}_0^D\bigl (({\cal E}^+)^{\vee }, \mathcal {Q}, s^{\vee }\bigr )$
over
${\mathbb V}_0^D\bigl (({\cal E}^+)^{\vee }, \mathcal {Q}, s^{\vee }\bigr )$
over
![]() $\mathcal {X}$
. Consider the morphism of adic spaces
$\mathcal {X}$
. Consider the morphism of adic spaces
defined on points as follows. Fix a morphism of adic spaces
![]() $\gamma \colon {\cal Z}\rightarrow \mathcal {X}$
. Consider
$\gamma \colon {\cal Z}\rightarrow \mathcal {X}$
. Consider
![]() $h\in {\mathbb V}_0({\cal E}^+,s)\bigl (\gamma \colon {\cal Z}\rightarrow \mathcal {X}\bigr )$
and
$h\in {\mathbb V}_0({\cal E}^+,s)\bigl (\gamma \colon {\cal Z}\rightarrow \mathcal {X}\bigr )$
and
![]() $h'\in {\mathbb V}_0^D\bigl (({\cal E}^+)^{\vee }, \mathcal {Q}, s^{\vee }\bigr )\bigl (\gamma \colon {\cal Z}\rightarrow \mathcal {X}\bigr )$
. By definition, this is equivalent to giving morphisms of
$h'\in {\mathbb V}_0^D\bigl (({\cal E}^+)^{\vee }, \mathcal {Q}, s^{\vee }\bigr )\bigl (\gamma \colon {\cal Z}\rightarrow \mathcal {X}\bigr )$
. By definition, this is equivalent to giving morphisms of
![]() ${\cal O}_{{\cal Z}}^+$
-modules
${\cal O}_{{\cal Z}}^+$
-modules
![]() $h\colon \gamma ^{\ast }({\cal E}^+)\rightarrow {\cal O}_{{\cal Z}}^+$
with
$h\colon \gamma ^{\ast }({\cal E}^+)\rightarrow {\cal O}_{{\cal Z}}^+$
with
![]() $h(\mathrm {mod}\ {\cal I})(\gamma ^{\ast }(s))=1$
and
$h(\mathrm {mod}\ {\cal I})(\gamma ^{\ast }(s))=1$
and
![]() $h'\colon \gamma ^{\ast }({\cal E}^+)^{\vee }\rightarrow {\cal O}_{{\cal Z}}^+$
with
$h'\colon \gamma ^{\ast }({\cal E}^+)^{\vee }\rightarrow {\cal O}_{{\cal Z}}^+$
with
![]() $h'(\mathrm {mod}\ \gamma ^{\ast }({\cal I}))(\mathcal {Q})=0$
and
$h'(\mathrm {mod}\ \gamma ^{\ast }({\cal I}))(\mathcal {Q})=0$
and
![]() $h'(\mathrm {mod}\ \gamma ^{\ast }({\cal I}))(\gamma ^{\ast }(s^{\vee }))=1$
. Then
$h'(\mathrm {mod}\ \gamma ^{\ast }({\cal I}))(\gamma ^{\ast }(s^{\vee }))=1$
. Then
![]() $h'(h)\in \mathrm {H}^0({\cal Z}, {\cal O}_{{\cal Z}}^+)$
and
$h'(h)\in \mathrm {H}^0({\cal Z}, {\cal O}_{{\cal Z}}^+)$
and
![]() $h'(h)(\mathrm {mod}\ \gamma ^{\ast }({\cal I}))=1$
, that is,
$h'(h)(\mathrm {mod}\ \gamma ^{\ast }({\cal I}))=1$
, that is,
![]() $h'(h)\in {\mathbb V}_0({\cal O}_{\mathcal {X}}^+, 1)\bigl (\gamma \colon {\cal Z}\rightarrow \mathcal {X} \bigr )$
. We define
$h'(h)\in {\mathbb V}_0({\cal O}_{\mathcal {X}}^+, 1)\bigl (\gamma \colon {\cal Z}\rightarrow \mathcal {X} \bigr )$
. We define
Notice that
![]() ${\mathbb V}_0({\cal O}_{\mathcal {X}}^+, 1)$
is the affine one-dimensional space
${\mathbb V}_0({\cal O}_{\mathcal {X}}^+, 1)$
is the affine one-dimensional space
![]() $\mathbb {A}^1_{\mathcal {X}}$
over
$\mathbb {A}^1_{\mathcal {X}}$
over
![]() $\mathcal {X}$
, with standard coordinate T. The torus
$\mathcal {X}$
, with standard coordinate T. The torus
![]() ${\cal T} \times {\cal T}$
acts componentwisely on
${\cal T} \times {\cal T}$
acts componentwisely on
![]() ${\mathbb V}_0({\cal E}^+, s)\times _{\mathcal {X}}{\mathbb V}_0^D\bigl (({\cal E}^+)^{\vee }, \mathcal {Q}, s^{\vee }\bigr )$
. Given sections
${\mathbb V}_0({\cal E}^+, s)\times _{\mathcal {X}}{\mathbb V}_0^D\bigl (({\cal E}^+)^{\vee }, \mathcal {Q}, s^{\vee }\bigr )$
. Given sections
![]() $(h,h')$
of the latter and
$(h,h')$
of the latter and
![]() $(u,u')$
of
$(u,u')$
of
![]() ${\cal T}\times {\cal T}$
, we have
${\cal T}\times {\cal T}$
, we have
![]() $\langle u \ast h, u' \ast h'\rangle =(u \cdot u') \ast \langle h, h'\rangle $
.
$\langle u \ast h, u' \ast h'\rangle =(u \cdot u') \ast \langle h, h'\rangle $
.
Lemma 3.4. There is a section
![]() $T^{k^{\mathrm {univ}}}$
of
$T^{k^{\mathrm {univ}}}$
of
![]() ${\mathbb W}_{k^{\mathrm {univ}}}({\cal O}_{\mathcal {X}}^+, 1)$
over
${\mathbb W}_{k^{\mathrm {univ}}}({\cal O}_{\mathcal {X}}^+, 1)$
over
![]() $\mathcal {X}$
such that
$\mathcal {X}$
such that
![]() ${\mathbb W}_{k^{\mathrm {univ}}}({\cal O}_{\mathcal {X}}^+, 1)= T^{k^{\mathrm {univ}}} \cdot {\cal O}_{\mathcal {X}}^+$
. Moreover,
${\mathbb W}_{k^{\mathrm {univ}}}({\cal O}_{\mathcal {X}}^+, 1)= T^{k^{\mathrm {univ}}} \cdot {\cal O}_{\mathcal {X}}^+$
. Moreover,
![]() $\langle\ {,}\ \rangle ^{\ast }\bigl (T^{k^{\mathrm {univ}}}\bigr )\in {\mathbb W}_{k^{\mathrm {univ}}}({\cal E}^+, s) \widehat {\otimes } {\mathbb W}^D_{k^{\mathrm { univ}}}\bigl (({\cal E}^+)^{\vee },\mathcal {Q}, s^{\vee } \bigr )$
. Here, we see
$\langle\ {,}\ \rangle ^{\ast }\bigl (T^{k^{\mathrm {univ}}}\bigr )\in {\mathbb W}_{k^{\mathrm {univ}}}({\cal E}^+, s) \widehat {\otimes } {\mathbb W}^D_{k^{\mathrm { univ}}}\bigl (({\cal E}^+)^{\vee },\mathcal {Q}, s^{\vee } \bigr )$
. Here, we see
![]() $\langle \ {,}\ \rangle ^{\ast }$
in a natural way, as a morphism of sheaves
$\langle \ {,}\ \rangle ^{\ast }$
in a natural way, as a morphism of sheaves
![]() ${\mathbb W}_{k^{\mathrm {univ}}}\bigl ({\cal O}_{\mathcal {X}}^+, 1 \bigr )\longrightarrow {\mathbb W}_{k^{\mathrm {univ}}}({\cal E}^+, s) \widehat {\otimes } {\mathbb W}^D_{k^{\mathrm {univ}}}\bigl (({\cal E}^+)^{\vee },\mathcal {Q}, s^{\vee } \bigr )$
.
${\mathbb W}_{k^{\mathrm {univ}}}\bigl ({\cal O}_{\mathcal {X}}^+, 1 \bigr )\longrightarrow {\mathbb W}_{k^{\mathrm {univ}}}({\cal E}^+, s) \widehat {\otimes } {\mathbb W}^D_{k^{\mathrm {univ}}}\bigl (({\cal E}^+)^{\vee },\mathcal {Q}, s^{\vee } \bigr )$
.
Proof. The statement is local on
![]() $\mathcal {X}$
. We use the explicit coordinates of §3.3.1. Then,
$\mathcal {X}$
. We use the explicit coordinates of §3.3.1. Then,
![]() $T=1+\alpha V$
and
$T=1+\alpha V$
and
![]() $T^{k^{\mathrm {univ}}}$
is the section
$T^{k^{\mathrm {univ}}}$
is the section
![]() $ k^{\mathrm {univ}}(1+\alpha V)$
. By loc. cit., we have
$ k^{\mathrm {univ}}(1+\alpha V)$
. By loc. cit., we have
![]() ${\mathbb W}_{k^{\mathrm {univ}}}({\cal O}_{\mathcal {X}}^+, 1)(U)= T^{k^{\mathrm {univ}}} \cdot R^+$
.
${\mathbb W}_{k^{\mathrm {univ}}}({\cal O}_{\mathcal {X}}^+, 1)(U)= T^{k^{\mathrm {univ}}} \cdot R^+$
.
As
![]() $\langle \ , \ \rangle ^{\ast }\bigl ( T \bigr )=X\otimes A + Y \otimes B=\big (1+\alpha Z )\big ) \cdot \bigl (1+\alpha C \bigr )+ \alpha Y \otimes D$
, we conclude that
$\langle \ , \ \rangle ^{\ast }\bigl ( T \bigr )=X\otimes A + Y \otimes B=\big (1+\alpha Z )\big ) \cdot \bigl (1+\alpha C \bigr )+ \alpha Y \otimes D$
, we conclude that
 $$ \begin{align} \langle \ , \ \rangle^{\ast}\bigl( T^{k^{\mathrm{univ}}} \bigr)=k^{\mathrm{univ}}(1+\alpha Z) k^{\mathrm{univ}}(1+\alpha C) \cdot k^{\mathrm{univ}}\left(1+\alpha \frac{Y}{1+\alpha Z} \otimes \frac{D}{1+\alpha C}\right). \end{align} $$
$$ \begin{align} \langle \ , \ \rangle^{\ast}\bigl( T^{k^{\mathrm{univ}}} \bigr)=k^{\mathrm{univ}}(1+\alpha Z) k^{\mathrm{univ}}(1+\alpha C) \cdot k^{\mathrm{univ}}\left(1+\alpha \frac{Y}{1+\alpha Z} \otimes \frac{D}{1+\alpha C}\right). \end{align} $$
This concludes the proof.
Definition 3.5. Write
![]() ${\mathbb W}_{k^{\mathrm {univ}}}({\cal E}^+, s)^{\vee }$
for the
${\mathbb W}_{k^{\mathrm {univ}}}({\cal E}^+, s)^{\vee }$
for the
![]() ${\cal O}_{\mathcal {X}}^+$
-dual of
${\cal O}_{\mathcal {X}}^+$
-dual of
![]() ${\mathbb W}_{k^{\mathrm {univ}}}({\cal E}^+, s)$
. Define the map of
${\mathbb W}_{k^{\mathrm {univ}}}({\cal E}^+, s)$
. Define the map of
![]() ${\cal O}_{\mathcal {X}}^+$
-modules
${\cal O}_{\mathcal {X}}^+$
-modules
3.4.1 Local descriptions of the duality between
 ${\mathbb W}_k$
and
${\mathbb W}_k$
and
 ${\mathbb W}_k^D$
${\mathbb W}_k^D$
We put ourselves in the setting of §3.3.1 and compute explicitly the pairing
![]() $\xi _{k^{\mathrm {univ}}}$
on the affinoid U in terms of the local coordinates of loc. cit. As
$\xi _{k^{\mathrm {univ}}}$
on the affinoid U in terms of the local coordinates of loc. cit. As
![]() $k^{\mathrm {univ}}$
is supposed to be r-analytic on
$k^{\mathrm {univ}}$
is supposed to be r-analytic on
![]() $\mathcal {X}$
, we can write
$\mathcal {X}$
, we can write
![]() $k^{\mathrm {univ}}(t)=\exp u_{\mathrm {univ}} \log (t)$
for every
$k^{\mathrm {univ}}(t)=\exp u_{\mathrm {univ}} \log (t)$
for every
![]() $t\in 1+p^r {\mathbb Z}_p$
. We then claim that
$t\in 1+p^r {\mathbb Z}_p$
. We then claim that
 $$ \begin{align*} \xi_{k^{\mathrm{univ}}}\left( k^{\mathrm{ univ}}(1+\alpha Z) \bigl(\frac{Y}{1+\alpha Z} \bigr)^n\right)^{\vee}=\alpha^n \left( \begin{matrix}u_{\mathrm{univ}} \cr n \cr \end{matrix}\right) k^{\mathrm{univ}}(1+\alpha C) \bigl(\frac{D}{1+\alpha C}\bigr)^n , \end{align*} $$
$$ \begin{align*} \xi_{k^{\mathrm{univ}}}\left( k^{\mathrm{ univ}}(1+\alpha Z) \bigl(\frac{Y}{1+\alpha Z} \bigr)^n\right)^{\vee}=\alpha^n \left( \begin{matrix}u_{\mathrm{univ}} \cr n \cr \end{matrix}\right) k^{\mathrm{univ}}(1+\alpha C) \bigl(\frac{D}{1+\alpha C}\bigr)^n , \end{align*} $$
where
 $\displaystyle \left ( \begin {matrix}u_{\mathrm {univ}} \cr n \cr \end {matrix}\right ) :=\frac { u_{\mathrm {univ}} (u_{\mathrm {univ}}-1) \cdots (u_{\mathrm {univ}}-n+1)}{n!}$
if
$\displaystyle \left ( \begin {matrix}u_{\mathrm {univ}} \cr n \cr \end {matrix}\right ) :=\frac { u_{\mathrm {univ}} (u_{\mathrm {univ}}-1) \cdots (u_{\mathrm {univ}}-n+1)}{n!}$
if
![]() $n\ge 1$
and
$n\ge 1$
and
 $\displaystyle \left ( \begin {matrix}u_{\mathrm {univ}} \cr 0 \cr \end {matrix}\right )=1$
.
$\displaystyle \left ( \begin {matrix}u_{\mathrm {univ}} \cr 0 \cr \end {matrix}\right )=1$
.
First of all, one computes that, if we write
![]() $f(X):=\exp u_{\mathrm {univ}} \log (1+X)=\sum _{n=0}^{\infty } a_n X^n$
as a formal power series in X, then
$f(X):=\exp u_{\mathrm {univ}} \log (1+X)=\sum _{n=0}^{\infty } a_n X^n$
as a formal power series in X, then
 $\displaystyle a_n= \left ( \begin {matrix}u_{\mathrm {univ}} \cr n \cr \end {matrix}\right )$
. Using equation (1), we deduce that
$\displaystyle a_n= \left ( \begin {matrix}u_{\mathrm {univ}} \cr n \cr \end {matrix}\right )$
. Using equation (1), we deduce that
 $$ \begin{align*} \frac{\langle \ , \ \rangle^{\ast}\bigl( T^{k^{\mathrm{univ}}} \bigr)}{k^{\mathrm{univ}}(1+\alpha Z) k^{\mathrm{univ}}(1+\alpha C)}= \sum_ {n=0}^{\infty} \alpha^n \left( \begin{matrix}u_{\mathrm{univ}} \cr n \cr \end{matrix}\right) \left(\frac{Y}{1+\alpha Z} \right)^n\otimes \left(\frac{D}{1+\alpha C} \right)^n, \end{align*} $$
$$ \begin{align*} \frac{\langle \ , \ \rangle^{\ast}\bigl( T^{k^{\mathrm{univ}}} \bigr)}{k^{\mathrm{univ}}(1+\alpha Z) k^{\mathrm{univ}}(1+\alpha C)}= \sum_ {n=0}^{\infty} \alpha^n \left( \begin{matrix}u_{\mathrm{univ}} \cr n \cr \end{matrix}\right) \left(\frac{Y}{1+\alpha Z} \right)^n\otimes \left(\frac{D}{1+\alpha C} \right)^n, \end{align*} $$
and the claim follows.
3.5 An example: locally analytic functions and distributions
We consider in this article weights defined as follows. Let
![]() ${\cal W}$
denote the weight space seen as an adic space.
${\cal W}$
denote the weight space seen as an adic space.
Definition 3.6. Let
![]() $U\subset {\cal W}$
be an open disk of an open affinoid of
$U\subset {\cal W}$
be an open disk of an open affinoid of
![]() ${\cal W}$
, and let
${\cal W}$
, and let
![]() $\Lambda _U$
denote the
$\Lambda _U$
denote the
![]() ${\mathbb Z}_p$
-subalgebra of sections in
${\mathbb Z}_p$
-subalgebra of sections in
![]() ${\cal O}_U^+(U)$
which are bounded; see Section §4 of [Reference Andreatta, Iovita and Stevens5]. We recall that
${\cal O}_U^+(U)$
which are bounded; see Section §4 of [Reference Andreatta, Iovita and Stevens5]. We recall that
![]() $\Lambda _U$
is a complete noetherian local
$\Lambda _U$
is a complete noetherian local
![]() ${\mathbb Z}_p$
-algebra, and we call ‘weak topology’ the
${\mathbb Z}_p$
-algebra, and we call ‘weak topology’ the
![]() $m_{\Lambda _U}$
-adic topology of
$m_{\Lambda _U}$
-adic topology of
![]() $\Lambda _U$
, where
$\Lambda _U$
, where
![]() $m_{\Lambda _U}$
is its maximal ideal. Let B denote either
$m_{\Lambda _U}$
is its maximal ideal. Let B denote either
![]() $\Lambda _U$
for some open disk
$\Lambda _U$
for some open disk
![]() $U\subset {\cal W}$
or
$U\subset {\cal W}$
or
![]() ${\cal O}_K$
for a finite extension K of
${\cal O}_K$
for a finite extension K of
![]() ${\mathbb Q}_p$
. In this article, we will work with B-valued weights
${\mathbb Q}_p$
. In this article, we will work with B-valued weights
![]() $k\colon {\mathbb Z}_p^{\ast }\longrightarrow B^{\ast }$
, which, if
$k\colon {\mathbb Z}_p^{\ast }\longrightarrow B^{\ast }$
, which, if
![]() $B=\Lambda _U$
, is the universal weight associated to U.
$B=\Lambda _U$
, is the universal weight associated to U.
Let
![]() $k\colon {\mathbb Z}_p^{\ast }\longrightarrow B^{\ast }$
be a weight as in definition 3.6, and suppose it is an r-analytic character. Let
$k\colon {\mathbb Z}_p^{\ast }\longrightarrow B^{\ast }$
be a weight as in definition 3.6, and suppose it is an r-analytic character. Let
![]() $T={\mathbb Z}_p\oplus {\mathbb Z}_p$
; denote by
$T={\mathbb Z}_p\oplus {\mathbb Z}_p$
; denote by
![]() $f_0=(1,0)$
and
$f_0=(1,0)$
and
![]() $f_1=(0,1)\in T$
the standard
$f_1=(0,1)\in T$
the standard
![]() ${\mathbb Z}_p$
-basis. Denote by
${\mathbb Z}_p$
-basis. Denote by
![]() $T^{\vee }$
the
$T^{\vee }$
the
![]() ${\mathbb Z}_p$
-dual of T, and let
${\mathbb Z}_p$
-dual of T, and let
![]() $T_0^{\vee } \subset T^{\vee }$
be the subset of elements
$T_0^{\vee } \subset T^{\vee }$
be the subset of elements
![]() ${\mathbb Z}_p^{\ast } e_0 \times {\mathbb Z}_p e_1 $
with
${\mathbb Z}_p^{\ast } e_0 \times {\mathbb Z}_p e_1 $
with
![]() $e_0=f_0^{\vee }$
and
$e_0=f_0^{\vee }$
and
![]() $e_1=f_1^{\vee }$
, the
$e_1=f_1^{\vee }$
, the
![]() ${\mathbb Z}_p$
-basis of
${\mathbb Z}_p$
-basis of
![]() $T^{\vee }$
dual to
$T^{\vee }$
dual to
![]() $(f_0, f_1)$
. Then
$(f_0, f_1)$
. Then
![]() $T_0^{\vee }$
is a profinite set with an action of the Iwahori subgroup
$T_0^{\vee }$
is a profinite set with an action of the Iwahori subgroup
![]() $\mathrm {Iw}_1\subset \mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
. Following [Reference Barrera and Gao7, Def. 3.1], we set:
$\mathrm {Iw}_1\subset \mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
. Following [Reference Barrera and Gao7, Def. 3.1], we set:
Definition 3.7. For every integer
![]() $n\geq r$
, let
$n\geq r$
, let
![]() $A_{k}^o(T_0^{\vee })[n]$
denote the space of functions
$A_{k}^o(T_0^{\vee })[n]$
denote the space of functions
![]() $f\colon T_0^{\vee }\longrightarrow B$
such that
$f\colon T_0^{\vee }\longrightarrow B$
such that
(1) for every
![]() $a\in {\mathbb Z}_p^{\ast }$
,
$a\in {\mathbb Z}_p^{\ast }$
,
![]() $t\in T_0^{\vee }$
, we have
$t\in T_0^{\vee }$
, we have
![]() $f(at) = k(a) f(t)$
$f(at) = k(a) f(t)$
(2) the function
![]() $z\rightarrow f(e_0+ze_1)$
extends to an n-analytic function, that is, for every
$z\rightarrow f(e_0+ze_1)$
extends to an n-analytic function, that is, for every
![]() $i\in {\mathbb Z}/p^n {\mathbb Z}$
the function
$i\in {\mathbb Z}/p^n {\mathbb Z}$
the function
![]() $f\bigl (e_0+(i+p^n z)e_1\bigr )$
for
$f\bigl (e_0+(i+p^n z)e_1\bigr )$
for
![]() $z\in {\mathbb Z}_p$
is given by the values of a convergent power series
$z\in {\mathbb Z}_p$
is given by the values of a convergent power series
![]() $\sum _{m=0}^{\infty } a_{m,i} z^m $
.
$\sum _{m=0}^{\infty } a_{m,i} z^m $
.
Define
![]() $D_k^o(T_0^{\vee })[n]:=\mathrm {Hom}_{B}\bigl (A_{k}^o(T_0^{\vee })[n], B\bigr )$
, the continuous dual of
$D_k^o(T_0^{\vee })[n]:=\mathrm {Hom}_{B}\bigl (A_{k}^o(T_0^{\vee })[n], B\bigr )$
, the continuous dual of
![]() $A_{k}^o(T_0^{\vee })[n]$
with respect to the weak topology of B. We write
$A_{k}^o(T_0^{\vee })[n]$
with respect to the weak topology of B. We write
![]() $A_{k}(T_0^{\vee })[n]:=A_{k}^o(T_0^{\vee })[n]\otimes _{\mathbb Z} {\mathbb Q}$
and
$A_{k}(T_0^{\vee })[n]:=A_{k}^o(T_0^{\vee })[n]\otimes _{\mathbb Z} {\mathbb Q}$
and
![]() $D_k(T_0^{\vee })[n]:=D_k^o(T_0^{\vee })[n]\otimes _{\mathbb Z} {\mathbb Q}$
.
$D_k(T_0^{\vee })[n]:=D_k^o(T_0^{\vee })[n]\otimes _{\mathbb Z} {\mathbb Q}$
.
By [Reference Barrera and Gao7, Lemma 3.1], the action of
![]() $\mathrm {Iw}_1$
on
$\mathrm {Iw}_1$
on
![]() $T_0^{\vee }$
induces actions of
$T_0^{\vee }$
induces actions of
![]() $\mathrm {Iw}_1$
on
$\mathrm {Iw}_1$
on
![]() $A_k^o(T_0^{\vee })[n]$
,
$A_k^o(T_0^{\vee })[n]$
,
![]() $D_k^o(T_0^{\vee })[n]$
,
$D_k^o(T_0^{\vee })[n]$
,
![]() $A_k(T_0^{\vee })[n]$
and
$A_k(T_0^{\vee })[n]$
and
![]() $D_k(T_0^{\vee })[n]$
. Moreover, [Reference Barrera and Gao7, Def. 3.3 & Prop. 3.3] the B module
$D_k(T_0^{\vee })[n]$
. Moreover, [Reference Barrera and Gao7, Def. 3.3 & Prop. 3.3] the B module
![]() $D_k^o(T_0^{\vee })[n]$
admits a decreasing filtration
$D_k^o(T_0^{\vee })[n]$
admits a decreasing filtration
![]() $\mathrm {Fil}^{\bullet } D_k^o(T_0^{\vee })[n]$
of B-modules, stable under the action of
$\mathrm {Fil}^{\bullet } D_k^o(T_0^{\vee })[n]$
of B-modules, stable under the action of
![]() $\mathrm {Iw}_1$
, such that the graded pieces are finite and
$\mathrm {Iw}_1$
, such that the graded pieces are finite and
![]() $D_k^o(T_0^{\vee })[n]$
is the inverse limit
$D_k^o(T_0^{\vee })[n]$
is the inverse limit
![]() $\displaystyle {\lim _{\infty \leftarrow m}} D_k^o(T_0^{\vee })[n]/\mathrm {Fil}^m D_k^o(T_0^{\vee })[n]$
.
$\displaystyle {\lim _{\infty \leftarrow m}} D_k^o(T_0^{\vee })[n]/\mathrm {Fil}^m D_k^o(T_0^{\vee })[n]$
.
3.5.1 An alternative description
For later purposes, we end this section by describing
![]() $A_k(T_0^{\vee })[n]$
and
$A_k(T_0^{\vee })[n]$
and
![]() $D_k(T_0^{\vee })[n]$
using the formalism of VBMS. For every
$D_k(T_0^{\vee })[n]$
using the formalism of VBMS. For every
![]() $\lambda =0,\ldots , p^n-1$
denote by
$\lambda =0,\ldots , p^n-1$
denote by
![]() ${\mathbb W}_k(T,s,t+\lambda s ,p^n)$
, or simply
${\mathbb W}_k(T,s,t+\lambda s ,p^n)$
, or simply
![]() ${\mathbb W}_k(T,s,t+\lambda s)$
if the power of p we are working with is clear from the context, the sections
${\mathbb W}_k(T,s,t+\lambda s)$
if the power of p we are working with is clear from the context, the sections
![]() ${\mathbb W}_{k}(T, s,t+\lambda s)(U)$
over the adic space
${\mathbb W}_{k}(T, s,t+\lambda s)(U)$
over the adic space
![]() $U=\mathrm {Spa}(B[1/p],B)$
associated to the rank
$U=\mathrm {Spa}(B[1/p],B)$
associated to the rank
![]() $2$
, free
$2$
, free
![]() ${\cal O}_U^+$
-module
${\cal O}_U^+$
-module
![]() $T\otimes {\cal O}^+_U$
and the two sections
$T\otimes {\cal O}^+_U$
and the two sections
![]() $s=f_0\otimes 1$
and
$s=f_0\otimes 1$
and
![]() $t+\lambda s=f_1\otimes 1+\lambda (f_0\otimes 1)$
modulo
$t+\lambda s=f_1\otimes 1+\lambda (f_0\otimes 1)$
modulo
![]() ${\cal I}:=p^n {\cal O}_U^+$
. Let
${\cal I}:=p^n {\cal O}_U^+$
. Let
![]() $\mathrm {Iw}_n$
be the subgroup of matrices
$\mathrm {Iw}_n$
be the subgroup of matrices
 $M=\left (\begin {matrix}\alpha & \beta \cr \gamma & \delta \end {matrix} \right )\in \mathrm {GL}_2({\mathbb Z}_p)$
such that
$M=\left (\begin {matrix}\alpha & \beta \cr \gamma & \delta \end {matrix} \right )\in \mathrm {GL}_2({\mathbb Z}_p)$
such that
![]() $\gamma \equiv 0$
modulo
$\gamma \equiv 0$
modulo
![]() $p^n$
. Then:
$p^n$
. Then:
Proposition 3.8. There is an
![]() $\mathrm {Iw}_n$
-equivariant isomorphism of B-modules
$\mathrm {Iw}_n$
-equivariant isomorphism of B-modules
Then, taking duals with respect to the weak topology on B, we get a decomposition into a direct sum and a
![]() $\mathrm {Iw}_n$
-equivariant isomorphism
$\mathrm {Iw}_n$
-equivariant isomorphism
Proof. We describe the isomorphism explicitly. First of all, notice that
![]() $A_k^o(T_0^{\vee })[n]$
decomposes as a direct sum
$A_k^o(T_0^{\vee })[n]$
decomposes as a direct sum
according to residue classes: We say that
![]() $f\in A_k^o(T_0^{\vee })[n]$
lies in
$f\in A_k^o(T_0^{\vee })[n]$
lies in
![]() $A_{k,\lambda }^o(T_0^{\vee })$
if an only if
$A_{k,\lambda }^o(T_0^{\vee })$
if an only if
![]() $f(1,w)$
is zero if
$f(1,w)$
is zero if
![]() $w\not \in \lambda + p^n {\mathbb Z}_p$
. In particular,
$w\not \in \lambda + p^n {\mathbb Z}_p$
. In particular,
where
![]() $\sum _{m=0}^{\infty } a_m w_{\lambda }^m \cdot u^k\colon T_0^{\vee } \to B$
sends
$\sum _{m=0}^{\infty } a_m w_{\lambda }^m \cdot u^k\colon T_0^{\vee } \to B$
sends
![]() $u e_0 + v e_1 \mapsto k(u) \cdot \sum _m a_m \bigl (\frac {v/u -\lambda }{p^n}\bigr )^m $
if
$u e_0 + v e_1 \mapsto k(u) \cdot \sum _m a_m \bigl (\frac {v/u -\lambda }{p^n}\bigr )^m $
if
![]() $v/u\in \lambda + p^n{\mathbb Z}_p$
and to
$v/u\in \lambda + p^n{\mathbb Z}_p$
and to
![]() $0$
otherwise. The standard left action of
$0$
otherwise. The standard left action of
![]() $\mathrm {Iw}_n$
on T is described as follows: Given
$\mathrm {Iw}_n$
on T is described as follows: Given
 $M=\left (\begin {matrix}\alpha & \beta \cr \gamma & \delta \end {matrix} \right )\in \mathrm {Iw}_n$
, we have
$M=\left (\begin {matrix}\alpha & \beta \cr \gamma & \delta \end {matrix} \right )\in \mathrm {Iw}_n$
, we have
![]() $M (f_0) =\alpha f_0 + \gamma f_1$
,
$M (f_0) =\alpha f_0 + \gamma f_1$
,
![]() $M(f_1)=\beta f_0 + \delta f_1$
. This induces a right action given by
$M(f_1)=\beta f_0 + \delta f_1$
. This induces a right action given by
![]() $e_0 \cdot M =\alpha e_0 + \beta e_1$
,
$e_0 \cdot M =\alpha e_0 + \beta e_1$
,
![]() $e_1 \cdot M=\gamma e_0 + \delta e_1$
. We finally obtain the left action of
$e_1 \cdot M=\gamma e_0 + \delta e_1$
. We finally obtain the left action of
![]() $\mathrm {Iw}_n$
on
$\mathrm {Iw}_n$
on
![]() $A_k^o(T_0^{\vee })[n]$
. Explicitly, as
$A_k^o(T_0^{\vee })[n]$
. Explicitly, as
![]() $(u e_0 + v e_1)\cdot M= (\alpha u +\gamma v) e_0 + (\beta u+ \delta v) e_1$
, then
$(u e_0 + v e_1)\cdot M= (\alpha u +\gamma v) e_0 + (\beta u+ \delta v) e_1$
, then
 $$ \begin{align*} M(w_0^m \cdot u^k ) = k(\alpha + \gamma w_0) \left(\frac{\beta + \delta w_0 }{\alpha +\gamma w_0}\right)^m \cdot u^k.\\[-9pt] \end{align*} $$
$$ \begin{align*} M(w_0^m \cdot u^k ) = k(\alpha + \gamma w_0) \left(\frac{\beta + \delta w_0 }{\alpha +\gamma w_0}\right)^m \cdot u^k.\\[-9pt] \end{align*} $$
As
 $w_{\lambda }^m \cdot u^k = \left (\begin {matrix} 1 & -\lambda \cr 0 & 1 \end {matrix}\right ) (w_0^m \cdot u^k) $
we get the sought for action of
$w_{\lambda }^m \cdot u^k = \left (\begin {matrix} 1 & -\lambda \cr 0 & 1 \end {matrix}\right ) (w_0^m \cdot u^k) $
we get the sought for action of
![]() $\mathrm {Iw}_n$
on
$\mathrm {Iw}_n$
on
![]() $\oplus _{\lambda =0}^{p^n-1} A_{k,\lambda }^o(T_0^{\vee })$
.
$\oplus _{\lambda =0}^{p^n-1} A_{k,\lambda }^o(T_0^{\vee })$
.
On the other hand, consider the subfunctors
![]() $\amalg _{\lambda =0}^{p^n-1} {\mathbb V}_0(T,s,t-\lambda s) \to {\mathbb V}(T)$
over the adic space
$\amalg _{\lambda =0}^{p^n-1} {\mathbb V}_0(T,s,t-\lambda s) \to {\mathbb V}(T)$
over the adic space
![]() $U=\mathrm {Spa}(B[1/p],B)$
. The action of
$U=\mathrm {Spa}(B[1/p],B)$
. The action of
![]() $\mathrm {Iw}_n$
on T restricts to an action on this subfunctors and induces an action on
$\mathrm {Iw}_n$
on T restricts to an action on this subfunctors and induces an action on
![]() $\oplus _{\lambda =0}^{p^n-1} {\mathbb W}_{k}(T, s,t-\lambda s)$
. Explicitly,
$\oplus _{\lambda =0}^{p^n-1} {\mathbb W}_{k}(T, s,t-\lambda s)$
. Explicitly,
according to §3.3.1. It contains the B-submodule of the space of integral functions
![]() $B\langle X,Y\rangle $
of
$B\langle X,Y\rangle $
of
![]() ${\mathbb V}(T\otimes {\cal O}_U^+)$
, where
${\mathbb V}(T\otimes {\cal O}_U^+)$
, where
![]() $X=1+p^n Z$
and
$X=1+p^n Z$
and
![]() $Y= p^n W_{\lambda }+\lambda X$
. Recall that we have a universal map
$Y= p^n W_{\lambda }+\lambda X$
. Recall that we have a universal map
![]() $T \to B\langle X,Y\rangle $
defined by sending
$T \to B\langle X,Y\rangle $
defined by sending
![]() $m f_0 + r f_1\mapsto m X + r Y$
. The left action of
$m f_0 + r f_1\mapsto m X + r Y$
. The left action of
![]() $\mathrm {Iw}_n$
on T defines by universality an action on
$\mathrm {Iw}_n$
on T defines by universality an action on
![]() $B\langle X,Y\rangle $
: If
$B\langle X,Y\rangle $
: If
 $M=\left (\begin {matrix} \alpha & \beta \cr \gamma & \delta \cr \end {matrix}\right )$
, then
$M=\left (\begin {matrix} \alpha & \beta \cr \gamma & \delta \cr \end {matrix}\right )$
, then
![]() $M (f_0) =\alpha f_0 + \gamma f_1$
,
$M (f_0) =\alpha f_0 + \gamma f_1$
,
![]() $M(f_1)=\beta f_0 + \delta f_1$
and
$M(f_1)=\beta f_0 + \delta f_1$
and
![]() $M(X)=\alpha X + \gamma Y$
,
$M(X)=\alpha X + \gamma Y$
,
![]() $M(Y)=\beta X + \delta Y$
. Denote by
$M(Y)=\beta X + \delta Y$
. Denote by
![]() $\mathrm {Iw}_n^1\subset \mathrm {Iw}_n$
the subgroup of matrices with
$\mathrm {Iw}_n^1\subset \mathrm {Iw}_n$
the subgroup of matrices with
![]() $\alpha =1 $
modulo
$\alpha =1 $
modulo
![]() $p^n$
. We then get an action of
$p^n$
. We then get an action of
![]() $\mathrm {Iw}_n^1$
on the integral functions on
$\mathrm {Iw}_n^1$
on the integral functions on
![]() $\amalg _{\lambda =0}^{p^n-1} {\mathbb V}_0(T,s,t-\lambda s)$
, and hence on
$\amalg _{\lambda =0}^{p^n-1} {\mathbb V}_0(T,s,t-\lambda s)$
, and hence on
![]() $\oplus _{\lambda } {\mathbb W}_k(T,s,t-\lambda s )$
, determined on the variables Z and
$\oplus _{\lambda } {\mathbb W}_k(T,s,t-\lambda s )$
, determined on the variables Z and
![]() $W_{\lambda }$
’s by the formulas
$W_{\lambda }$
’s by the formulas
 $$ \begin{align*}M(Z)=\frac{(\alpha X-1)}{p^n} + \gamma W_0,\quad M(W_0)=\frac{\beta}{p^n} X + \delta W_0, \quad \left(\begin{matrix} 1 &- \lambda \cr 0 & 1 \end{matrix}\right)(W_0)=W_{\lambda}. \end{align*} $$
$$ \begin{align*}M(Z)=\frac{(\alpha X-1)}{p^n} + \gamma W_0,\quad M(W_0)=\frac{\beta}{p^n} X + \delta W_0, \quad \left(\begin{matrix} 1 &- \lambda \cr 0 & 1 \end{matrix}\right)(W_0)=W_{\lambda}. \end{align*} $$
Notice that if
 $M=\left (\begin {matrix} \alpha & 0 \cr 0 & \delta \cr \end {matrix}\right ) \in \mathrm {Iw}_n$
, then
$M=\left (\begin {matrix} \alpha & 0 \cr 0 & \delta \cr \end {matrix}\right ) \in \mathrm {Iw}_n$
, then
![]() $M\bigl (k(1+p^n Z)\bigr )=k(\alpha ) k(1+p^n Z)$
and
$M\bigl (k(1+p^n Z)\bigr )=k(\alpha ) k(1+p^n Z)$
and
![]() $M(W_0)=\delta W_0$
giving explicitly the action of diagonal matrices on each
$M(W_0)=\delta W_0$
giving explicitly the action of diagonal matrices on each
![]() ${\mathbb W}_{k}(T, s,t-\lambda s)$
. For every
${\mathbb W}_{k}(T, s,t-\lambda s)$
. For every
![]() $\lambda =0,\ldots , p^n-1$
define the map
$\lambda =0,\ldots , p^n-1$
define the map
 $$ \begin{align*} \nu_{\lambda}\colon {\mathbb W}_{k}(T, s,t-\lambda s )\longrightarrow A_{k,\lambda}^o(T_0^{\vee})[n] , \quad k(1+p^n Z) \sum_i a_i \left(\frac{W_{\lambda}}{1+p^nZ}\right)^i\mapsto \sum_i a_i w_{\lambda}^i \cdot u^k. \end{align*} $$
$$ \begin{align*} \nu_{\lambda}\colon {\mathbb W}_{k}(T, s,t-\lambda s )\longrightarrow A_{k,\lambda}^o(T_0^{\vee})[n] , \quad k(1+p^n Z) \sum_i a_i \left(\frac{W_{\lambda}}{1+p^nZ}\right)^i\mapsto \sum_i a_i w_{\lambda}^i \cdot u^k. \end{align*} $$
It is clearly an isomorphism of B-modules. We are left to show that
 $$ \begin{align*} \nu_n:=\sum_{\lambda=0}^{p^n-1} \nu_{\lambda}\colon \oplus_{\lambda=0}^{p^n-1} {\mathbb W}_{k}(T, s,t-\lambda s)\to \oplus_{\lambda=0}^{p^n-1} A_{k,\lambda}^o(T_0^{\vee})[n]=A_k^o(T_0^{\vee})[n] \end{align*} $$
$$ \begin{align*} \nu_n:=\sum_{\lambda=0}^{p^n-1} \nu_{\lambda}\colon \oplus_{\lambda=0}^{p^n-1} {\mathbb W}_{k}(T, s,t-\lambda s)\to \oplus_{\lambda=0}^{p^n-1} A_{k,\lambda}^o(T_0^{\vee})[n]=A_k^o(T_0^{\vee})[n] \end{align*} $$
is
![]() $\mathrm {Iw}_n$
-equivariant.
$\mathrm {Iw}_n$
-equivariant.
Consider the B-linear map
![]() $\xi \colon B\langle X,Y\rangle \to A(T^{\vee })$
, where
$\xi \colon B\langle X,Y\rangle \to A(T^{\vee })$
, where
![]() $A(T^{\vee })$
is the ring of analytic functions from
$A(T^{\vee })$
is the ring of analytic functions from
![]() $T^{\vee }$
to B, sending
$T^{\vee }$
to B, sending
![]() $f(X,Y)=\sum _{h,m} a_{h,m} X^h Y^m$
to the function
$f(X,Y)=\sum _{h,m} a_{h,m} X^h Y^m$
to the function
![]() $\xi \bigl (f(X,Y)\bigr )\colon T^{\vee } \to B$
,
$\xi \bigl (f(X,Y)\bigr )\colon T^{\vee } \to B$
,
![]() $u e_0 + v e_1 \to \sum _{h,m} a_{h,m} u^hv^m$
. This map is
$u e_0 + v e_1 \to \sum _{h,m} a_{h,m} u^hv^m$
. This map is
![]() $\mathrm {Iw}_n$
-equivariant. Indeed, given
$\mathrm {Iw}_n$
-equivariant. Indeed, given
![]() $M\in \mathrm {Iw}_n$
such that
$M\in \mathrm {Iw}_n$
such that
![]() $M (f_0) =\alpha f_0 + \gamma f_1$
,
$M (f_0) =\alpha f_0 + \gamma f_1$
,
![]() $M(f_1)=\beta f_0 + \delta f_1$
then
$M(f_1)=\beta f_0 + \delta f_1$
then
![]() $M (e_0) =\alpha e_0 + \beta e_1$
,
$M (e_0) =\alpha e_0 + \beta e_1$
,
![]() $M(e_1)=\gamma e_0 + \delta e_1$
so that
$M(e_1)=\gamma e_0 + \delta e_1$
so that
![]() $M(u e_0 + v e_1)= (u \alpha + v \gamma ) e_0 + (u\beta + \delta v) e_1$
. Hence,
$M(u e_0 + v e_1)= (u \alpha + v \gamma ) e_0 + (u\beta + \delta v) e_1$
. Hence,
![]() $M\bigl (\xi (f(X,Y)) \bigr )=\xi \bigl (f\bigl (M(X),M(Y)\bigr )\bigr )$
. As
$M\bigl (\xi (f(X,Y)) \bigr )=\xi \bigl (f\bigl (M(X),M(Y)\bigr )\bigr )$
. As
![]() $\nu _n$
is determined by
$\nu _n$
is determined by
![]() $\xi $
using that
$\xi $
using that
![]() $X=1+p^nZ$
and
$X=1+p^nZ$
and
![]() $Y= p^n W_{\lambda }+\lambda X$
, this implies that
$Y= p^n W_{\lambda }+\lambda X$
, this implies that
![]() $\nu _n$
is
$\nu _n$
is
![]() $\mathrm {Iw}_n$
-equivariant as well.
$\mathrm {Iw}_n$
-equivariant as well.
Note that we have a
![]() $\mathrm {Iw}_n$
-equivariant map of functors, and hence of representing objects,
$\mathrm {Iw}_n$
-equivariant map of functors, and hence of representing objects,
![]() $\amalg _{\lambda \in {\mathbb Z}/p^n{\mathbb Z}}{\mathbb V}_0(T,s,t-\lambda s) \to {\mathbb V}_0(T,s)$
. This provides a
$\amalg _{\lambda \in {\mathbb Z}/p^n{\mathbb Z}}{\mathbb V}_0(T,s,t-\lambda s) \to {\mathbb V}_0(T,s)$
. This provides a
![]() $\mathrm {Iw}_n$
-equivariant map
$\mathrm {Iw}_n$
-equivariant map
Let
![]() $Q_n\subset T^{\vee }/p^n T^{\vee }$
be the
$Q_n\subset T^{\vee }/p^n T^{\vee }$
be the
![]() $({\mathbb Z}/p^n{\mathbb Z})$
-dual of the quotient
$({\mathbb Z}/p^n{\mathbb Z})$
-dual of the quotient
![]() $\bigl (T/p^n T\bigr )/ ({\mathbb Z}/p^n{\mathbb Z}) s$
. The duality between
$\bigl (T/p^n T\bigr )/ ({\mathbb Z}/p^n{\mathbb Z}) s$
. The duality between
of Definition 3.5 composed with the
![]() $\mathrm {Iw}_n$
-equivariant isomorphism
$\mathrm {Iw}_n$
-equivariant isomorphism
of Proposition 3.8 give the following.
Corollary 3.9. We have a
![]() $\mathrm {Iw}_n$
-equivariant, B-linear map
$\mathrm {Iw}_n$
-equivariant, B-linear map
3.5.2 The
 $U_p$
operator
$U_p$
operator
For
![]() $\rho =0,\ldots ,p-1$
, let
$\rho =0,\ldots ,p-1$
, let
![]() $\pi _{\rho }\colon T \to T$
be the map defined by
$\pi _{\rho }\colon T \to T$
be the map defined by
 $\left (\begin {matrix} 1 & \rho \cr 0 & p \cr \end {matrix}\right ) $
, that is,
$\left (\begin {matrix} 1 & \rho \cr 0 & p \cr \end {matrix}\right ) $
, that is,
![]() $f_0\mapsto f_0$
,
$f_0\mapsto f_0$
,
![]() $f_1\mapsto p f_1+ \rho f_0$
. It defines the map
$f_1\mapsto p f_1+ \rho f_0$
. It defines the map
![]() $\pi _{\rho }^{\vee }\colon T^{\vee } \to T^{\vee }$
that sends
$\pi _{\rho }^{\vee }\colon T^{\vee } \to T^{\vee }$
that sends
![]() $u e_0+ v e_1 \mapsto u e_0+(pv+\rho ) e_1$
. In particular, taking
$u e_0+ v e_1 \mapsto u e_0+(pv+\rho ) e_1$
. In particular, taking
![]() $(\pi _{\rho }^{\vee })^{\ast }$
it induces a map
$(\pi _{\rho }^{\vee })^{\ast }$
it induces a map
![]() $A_{k}^o(T_0^{\vee })[n+1] \to A_{k}^o(T_0^{\vee })[n]$
that is
$A_{k}^o(T_0^{\vee })[n+1] \to A_{k}^o(T_0^{\vee })[n]$
that is
![]() $0$
on
$0$
on
![]() $A_{k,\lambda }^o(T_0^{\vee })[n+1] $
for
$A_{k,\lambda }^o(T_0^{\vee })[n+1] $
for
![]() $\lambda \not \equiv \rho $
modulo p and it induces a map
$\lambda \not \equiv \rho $
modulo p and it induces a map
![]() $A_{k,\lambda }^o(T_0^{\vee })[n+1] \to A_{k,\lambda _0}^o(T_0^{\vee })[n] $
if
$A_{k,\lambda }^o(T_0^{\vee })[n+1] \to A_{k,\lambda _0}^o(T_0^{\vee })[n] $
if
![]() $\lambda =\rho + p \lambda _0$
, with
$\lambda =\rho + p \lambda _0$
, with
![]() $\lambda _0\in \{ 0,\ldots , p^n-1\}$
. Taking the sum over the
$\lambda _0\in \{ 0,\ldots , p^n-1\}$
. Taking the sum over the
![]() $\rho $
’s, we get a map
$\rho $
’s, we get a map
![]() $\pi _n=\sum _{\rho =0}^{p-1} (\pi _{\rho }^{\vee })^{\ast }$
, where
$\pi _n=\sum _{\rho =0}^{p-1} (\pi _{\rho }^{\vee })^{\ast }$
, where
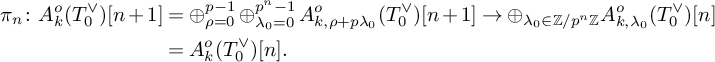 $$ \begin{align*} \pi_n \colon A_{k}^o(T_0^{\vee})[n+1]&=\oplus_{\rho=0}^{p-1} \oplus_{\lambda_0=0}^{p^n-1} A_{k,\rho+p\lambda_0}^o(T_0^{\vee})[n+1] \to \oplus_{\lambda_0\in{\mathbb Z}/p^n {\mathbb Z}} A_{k,\lambda_0}^o(T_0^{\vee})[n]\\&=A_{k}^o(T_0^{\vee})[n]. \end{align*} $$
$$ \begin{align*} \pi_n \colon A_{k}^o(T_0^{\vee})[n+1]&=\oplus_{\rho=0}^{p-1} \oplus_{\lambda_0=0}^{p^n-1} A_{k,\rho+p\lambda_0}^o(T_0^{\vee})[n+1] \to \oplus_{\lambda_0\in{\mathbb Z}/p^n {\mathbb Z}} A_{k,\lambda_0}^o(T_0^{\vee})[n]\\&=A_{k}^o(T_0^{\vee})[n]. \end{align*} $$
Notice that
![]() $\pi _{\rho }$
defines by functoriality a map
$\pi _{\rho }$
defines by functoriality a map
![]() ${\mathbb V}_0(T,s,t-\lambda s,p^n) \to {\mathbb V}_0(T,s,t-(\rho +p\lambda ) s,p^{n+1})$
(we have added the dependence on the power of p in the definition of
${\mathbb V}_0(T,s,t-\lambda s,p^n) \to {\mathbb V}_0(T,s,t-(\rho +p\lambda ) s,p^{n+1})$
(we have added the dependence on the power of p in the definition of
![]() ${\mathbb V}_0$
to avoid confusion). This gives a map
${\mathbb V}_0$
to avoid confusion). This gives a map
![]() $\mu _{\rho }\colon {\mathbb W}_{k}(T, s,t-(\rho +p\lambda ) s,p^{n+1})\to {\mathbb W}_k( s, t-\lambda s,p^{n}) $
and, summing over all
$\mu _{\rho }\colon {\mathbb W}_{k}(T, s,t-(\rho +p\lambda ) s,p^{n+1})\to {\mathbb W}_k( s, t-\lambda s,p^{n}) $
and, summing over all
![]() $\rho $
’s,
$\rho $
’s,
 $$ \begin{align*} \mu_n=\sum_{\rho=0}^{p-1}\mu_{\rho}\colon\oplus_{\rho=0}^{p-1}\oplus_{\lambda=0}^{p^n-1} {\mathbb W}_{k}(T, s,t-(\rho+p\lambda) s,p^{n+1})\to \oplus_{\lambda\in {\mathbb Z}/p^n{\mathbb Z}} {\mathbb W}_{k}(T, s,t-\lambda s,p^{n}). \end{align*} $$
$$ \begin{align*} \mu_n=\sum_{\rho=0}^{p-1}\mu_{\rho}\colon\oplus_{\rho=0}^{p-1}\oplus_{\lambda=0}^{p^n-1} {\mathbb W}_{k}(T, s,t-(\rho+p\lambda) s,p^{n+1})\to \oplus_{\lambda\in {\mathbb Z}/p^n{\mathbb Z}} {\mathbb W}_{k}(T, s,t-\lambda s,p^{n}). \end{align*} $$
Lemma 3.10. With the notation of Proposition 3.8, we have
![]() $\pi _n \circ \nu _{n+1}=\nu _n \circ \mu _n$
and similarly taking strong duals
$\pi _n \circ \nu _{n+1}=\nu _n \circ \mu _n$
and similarly taking strong duals
![]() $ \nu _{n+1}^{\vee } \circ \pi _n^{\vee }=\mu _n^{\vee } \circ \nu _n^{\vee }$
.
$ \nu _{n+1}^{\vee } \circ \pi _n^{\vee }=\mu _n^{\vee } \circ \nu _n^{\vee }$
.
Proof. This is an explicit computation using the notation of the proof of Proposition 3.8 and follows from the fact that
![]() $ (\pi _{\rho }^{\vee })^{\ast }$
sends
$ (\pi _{\rho }^{\vee })^{\ast }$
sends
![]() $w_{\rho +p\lambda _0} \mapsto w_{\lambda _0}$
and
$w_{\rho +p\lambda _0} \mapsto w_{\lambda _0}$
and
![]() $\mu _{\lambda }$
sends
$\mu _{\lambda }$
sends
![]() $W_{\rho +p\lambda }\mapsto W_{\lambda }$
.
$W_{\rho +p\lambda }\mapsto W_{\lambda }$
.
4 The modular curve setting
Let
![]() $p>0$
be a prime integer. We fix once for all the p-adic completion
$p>0$
be a prime integer. We fix once for all the p-adic completion
![]() ${\mathbb C}_p$
of an algebraic closure of
${\mathbb C}_p$
of an algebraic closure of
![]() ${\mathbb Q}_p$
. We denote by v the valuation on
${\mathbb Q}_p$
. We denote by v the valuation on
![]() ${\mathbb C}_p$
, normalized such that
${\mathbb C}_p$
, normalized such that
![]() $v(p)=1$
.
$v(p)=1$
.
Let
![]() $N\geq 5$
and
$N\geq 5$
and
![]() $r\geq 0$
be integers with N prime to p, and let
$r\geq 0$
be integers with N prime to p, and let
![]() $X_0(p^r,N)$
, resp.
$X_0(p^r,N)$
, resp.
![]() $X_1(p^r,N)$
, resp.
$X_1(p^r,N)$
, resp.
![]() $X(p^r,N)$
, be the modular curves over
$X(p^r,N)$
, be the modular curves over
![]() ${\mathbb C}_p$
of level
${\mathbb C}_p$
of level
![]() $\Gamma _1(N) \cap \Gamma _0(p^r)$
, resp.
$\Gamma _1(N) \cap \Gamma _0(p^r)$
, resp.
![]() $\Gamma _1(N)\cap \Gamma _1(p^r) $
, resp.
$\Gamma _1(N)\cap \Gamma _1(p^r) $
, resp.
![]() $\Gamma _1(N)\cap \Gamma (p^r) $
. Over the complement of the cusps of the modular curve
$\Gamma _1(N)\cap \Gamma (p^r) $
. Over the complement of the cusps of the modular curve
![]() $X_0(p^s,N) $
, we have a universal elliptic curve E, a cyclic subgroup
$X_0(p^s,N) $
, we have a universal elliptic curve E, a cyclic subgroup
![]() $H_s\subset E[p^s]$
of order
$H_s\subset E[p^s]$
of order
![]() $p^s$
and an embedding
$p^s$
and an embedding
![]() $\Psi _N\colon \mu _N\hookrightarrow E[N]$
. For
$\Psi _N\colon \mu _N\hookrightarrow E[N]$
. For
![]() $X_1(p^s,N) $
, we further have a generator of
$X_1(p^s,N) $
, we further have a generator of
![]() $H_s$
.
$H_s$
.
We denote the associated adic space over
![]() $\mathrm {Spa}({\mathbb C}_p,{\cal O}_{{\mathbb C}_p}\big )$
by
$\mathrm {Spa}({\mathbb C}_p,{\cal O}_{{\mathbb C}_p}\big )$
by
![]() $\mathcal {X}_0(p^r,N)$
, resp.
$\mathcal {X}_0(p^r,N)$
, resp.
![]() $\mathcal {X}_1(p^r,N)$
, resp.
$\mathcal {X}_1(p^r,N)$
, resp.
![]() $\mathcal {X}(p^r,N)$
considered as adic spaces with logarithmic structures given by the cusps, with reduced structure, as in [Reference Diao, Lan, Liu and Zhu15, Ex. 2.3.17]. We simply write X, resp.
$\mathcal {X}(p^r,N)$
considered as adic spaces with logarithmic structures given by the cusps, with reduced structure, as in [Reference Diao, Lan, Liu and Zhu15, Ex. 2.3.17]. We simply write X, resp.
![]() $\mathcal {X}$
for
$\mathcal {X}$
for
![]() $X_0(p^0,N)$
, resp.
$X_0(p^0,N)$
, resp.
![]() $\mathcal {X}(p^0,N)$
. Notice that the
$\mathcal {X}(p^0,N)$
. Notice that the
![]() $p^r$
-torsion of the universal elliptic curve E over the complement of the cusps in X defines a locally constant sheaf for the finite Kummer étale topology that we denote by
$p^r$
-torsion of the universal elliptic curve E over the complement of the cusps in X defines a locally constant sheaf for the finite Kummer étale topology that we denote by
![]() $E[p^r]$
and
$E[p^r]$
and
![]() $\mathcal {X}(p^r,N)\to \mathcal {X}$
is the finite Kummer étale Galois cover, with group
$\mathcal {X}(p^r,N)\to \mathcal {X}$
is the finite Kummer étale Galois cover, with group
![]() $\mathrm { \mathbf {GL}}_2({\mathbb Z}/p^r{\mathbb Z})$
, defined by trivializing it. We let
$\mathrm { \mathbf {GL}}_2({\mathbb Z}/p^r{\mathbb Z})$
, defined by trivializing it. We let
![]() $T_p(E)$
be the sheaf on
$T_p(E)$
be the sheaf on
![]() $X_{\mathrm {profket}}$
, resp.
$X_{\mathrm {profket}}$
, resp.
![]() $\mathcal {X}_{\mathrm {profket}}$
defined by the inverse limt
$\mathcal {X}_{\mathrm {profket}}$
defined by the inverse limt
![]() $\lim E[p^r]$
. Thanks to [Reference Scholze23, Thm. 3.1.2], we have
$\lim E[p^r]$
. Thanks to [Reference Scholze23, Thm. 3.1.2], we have
-
(i) a unique perfectoid space
 $\mathcal {X}(p^{\infty },N)$
such that
$\mathcal {X}(p^{\infty },N)$
such that
 $\mathcal {X}(p^{\infty },N) \sim \displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
in the sense of [Reference Scholze and Weinstein24, Def. 2.4.1];
$\mathcal {X}(p^{\infty },N) \sim \displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
in the sense of [Reference Scholze and Weinstein24, Def. 2.4.1]; -
(ii) the Hodge–Tate period map
 $\pi _{\mathrm {HT}}\colon \mathcal {X}(p^{\infty },N) \longrightarrow \mathbb {P}^1_{{\mathbb Q}_p}$
.
$\pi _{\mathrm {HT}}\colon \mathcal {X}(p^{\infty },N) \longrightarrow \mathbb {P}^1_{{\mathbb Q}_p}$
.
In particular, we have morphisms of adic spaces
![]() $\pi _r\colon \mathcal {X}(p^{\infty },N)\to \mathcal {X}(p^r,N)$
, compatible for varying
$\pi _r\colon \mathcal {X}(p^{\infty },N)\to \mathcal {X}(p^r,N)$
, compatible for varying
![]() $r \geq 0$
, inducing a homeomorphism of the underlying topological spaces
$r \geq 0$
, inducing a homeomorphism of the underlying topological spaces
![]() $\vert \mathcal {X}(p^{\infty },N) \vert \cong \displaystyle {\lim _{\infty \leftarrow r}} \vert \mathcal {X}(p^r,N) \vert $
.
$\vert \mathcal {X}(p^{\infty },N) \vert \cong \displaystyle {\lim _{\infty \leftarrow r}} \vert \mathcal {X}(p^r,N) \vert $
.
4.1 On the pro-Kummer étale topology of modular curves
For every
![]() $s\in {\mathbb N}$
, we write
$s\in {\mathbb N}$
, we write
![]() $\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
(for
$\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
(for
![]() $r\geq s$
) for the pro-finite Kummer étale cover of
$r\geq s$
) for the pro-finite Kummer étale cover of
![]() $\mathcal {X}_0(p^s,N)$
defined by the Kummer étale covers
$\mathcal {X}_0(p^s,N)$
defined by the Kummer étale covers
![]() $\mathcal {X}(p^r,N)\to \mathcal {X}_0(p^s,N)$
, for
$\mathcal {X}(p^r,N)\to \mathcal {X}_0(p^s,N)$
, for
![]() $r\geq s$
. The following lemma provides a basis for the pro-Kumemr étale topology of
$r\geq s$
. The following lemma provides a basis for the pro-Kumemr étale topology of
![]() $\mathcal {X}_0(p^s,N)$
:
$\mathcal {X}_0(p^s,N)$
:
Lemma 4.1. For every
![]() $s\in {\mathbb N}$
, the site
$s\in {\mathbb N}$
, the site
![]() $\mathcal {X}_0(p^s,N)_{\mathrm {pke}}$
has a basis consisting of log affinoid perfectoid opens U that are pro-Kummer étale over an affinoid perfectoid open of
$\mathcal {X}_0(p^s,N)_{\mathrm {pke}}$
has a basis consisting of log affinoid perfectoid opens U that are pro-Kummer étale over an affinoid perfectoid open of
![]() $\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
(for
$\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
(for
![]() $r\geq s$
). In particular, for any such open U,
$r\geq s$
). In particular, for any such open U,
![]() $T_p(E)\vert _U$
is a constant sheaf and such basis is closed under fibre products over
$T_p(E)\vert _U$
is a constant sheaf and such basis is closed under fibre products over
![]() $\mathcal {X}_0(p^s,N)$
.
$\mathcal {X}_0(p^s,N)$
.
Proof. Due to [Reference Diao, Lan, Liu and Zhu15, Prop. 5.3.12], the site
![]() $\mathcal {X}_0(p^s,N)_{\mathrm {pke}}$
admits a basis consisting of log affinoid perfectoid opens, and thanks to [Reference Diao, Lan, Liu and Zhu15, Prop. 5.3.11], the category of such bases is closed under fibre products. Given any such W, consider the fibre product Z of W and
$\mathcal {X}_0(p^s,N)_{\mathrm {pke}}$
admits a basis consisting of log affinoid perfectoid opens, and thanks to [Reference Diao, Lan, Liu and Zhu15, Prop. 5.3.11], the category of such bases is closed under fibre products. Given any such W, consider the fibre product Z of W and
![]() $\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
over
$\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
over
![]() $\mathcal {X}_0(p^s,N)$
. By [Reference Diao, Lan, Liu and Zhu15, Cor. 5.3.9] if such a fibre product exists, it is pro-Kummer étale over
$\mathcal {X}_0(p^s,N)$
. By [Reference Diao, Lan, Liu and Zhu15, Cor. 5.3.9] if such a fibre product exists, it is pro-Kummer étale over
![]() $\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
. As a cover of W, it can be represented as
$\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
. As a cover of W, it can be represented as
![]() $\displaystyle {\lim _{\infty \leftarrow r}} W_r$
with
$\displaystyle {\lim _{\infty \leftarrow r}} W_r$
with
![]() $W_r:=\mathcal {X}(p^r,N) \times _{\mathcal {X}_0(p^s,N)} W$
. In particular, thanks to [Reference Diao, Lan, Liu and Zhu15, Lemma 5.3.8], each
$W_r:=\mathcal {X}(p^r,N) \times _{\mathcal {X}_0(p^s,N)} W$
. In particular, thanks to [Reference Diao, Lan, Liu and Zhu15, Lemma 5.3.8], each
![]() $W_r$
is a finite étale cover of W so that
$W_r$
is a finite étale cover of W so that
![]() $Z=\displaystyle {\lim _{\infty \leftarrow r}} W_r \to W$
is a pro-finite étale cover of W. Since W is log affinoid perfectoid, we deduce from [Reference Diao, Lan, Liu and Zhu15, Cor. 5.3.9] that also Z is log affinoid perfectoid. Recall from [Reference Scholze23, Thm. 3.1.2] that
$Z=\displaystyle {\lim _{\infty \leftarrow r}} W_r \to W$
is a pro-finite étale cover of W. Since W is log affinoid perfectoid, we deduce from [Reference Diao, Lan, Liu and Zhu15, Cor. 5.3.9] that also Z is log affinoid perfectoid. Recall from [Reference Scholze23, Thm. 3.1.2] that
![]() $\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
is covered by perfectoid affinoid open subsets. Taking the fibre product over
$\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
is covered by perfectoid affinoid open subsets. Taking the fibre product over
![]() $\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
of Z with a cover of
$\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
of Z with a cover of
![]() $\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
by perfectoid affinoid open subsets, the claim follows.
$\displaystyle {\lim _{\infty \leftarrow r}} \mathcal {X}(p^r,N)$
by perfectoid affinoid open subsets, the claim follows.
Remark 4.2. Endow
![]() $\mathcal {X}(p^{\infty },N)$
with the limit log structure. Then, open affinoid subsets of
$\mathcal {X}(p^{\infty },N)$
with the limit log structure. Then, open affinoid subsets of
![]() $\mathcal {X}(p^{\infty },N)$
for the analytic topology are not log affinoid perfectoid opens as condition (d) of §2.3 is not satisfied.
$\mathcal {X}(p^{\infty },N)$
for the analytic topology are not log affinoid perfectoid opens as condition (d) of §2.3 is not satisfied.
This condition is used in [Reference Diao, Lan, Liu and Zhu15, Cor. 5.3.8], an analogue of Abhyankar’s lemma, stating that, for a log affinoid perfectoid, the finite Kummer étale site coincides with the finite étale site. This was already used in the proof of Lemma 4.1.
4.2 Standard opens
We start by defining certain opens of
![]() ${\mathbb P}^1:={\mathbb P}^1_{{\mathbb Q}_p}$
, namely let for every
${\mathbb P}^1:={\mathbb P}^1_{{\mathbb Q}_p}$
, namely let for every
![]() $n\ge 1 U_0, U_{\infty }, U_{\infty }^{(n)}, U_0^{(n)}\subset {\mathbb P}^1$
be defined as follows. Let T denote a parameter at
$n\ge 1 U_0, U_{\infty }, U_{\infty }^{(n)}, U_0^{(n)}\subset {\mathbb P}^1$
be defined as follows. Let T denote a parameter at
![]() $0$
on
$0$
on
![]() ${\mathbb P}^1$
, then
${\mathbb P}^1$
, then
-
a)
 $\displaystyle U_{\infty }=\{x\in {\mathbb P}^1 \ | \ \Vert \frac {1}{T}\Vert _x\le 1\}$
,
$\displaystyle U_{\infty }=\{x\in {\mathbb P}^1 \ | \ \Vert \frac {1}{T}\Vert _x\le 1\}$
,
 $U_0=\{x\in {\mathbb P}^1 \ | \ \Vert T-\lambda \Vert _x\le 1, \mbox { for some }\lambda \in \{0,1,\ldots ,p-1\}\}$
,
$U_0=\{x\in {\mathbb P}^1 \ | \ \Vert T-\lambda \Vert _x\le 1, \mbox { for some }\lambda \in \{0,1,\ldots ,p-1\}\}$
, -
b)
 $\displaystyle U_{\infty }^{(n)}={\mathbb P}^1\bigl ( \frac {1}{p^nT} \bigr )=\{x\in {\mathbb P}^1\ | \ \Vert \frac {1}{T}\Vert _x\le \Vert p^n\Vert _x\}$
,
$\displaystyle U_{\infty }^{(n)}={\mathbb P}^1\bigl ( \frac {1}{p^nT} \bigr )=\{x\in {\mathbb P}^1\ | \ \Vert \frac {1}{T}\Vert _x\le \Vert p^n\Vert _x\}$
, -
c)
 $U_0^{(n)}=\cup _{\lambda } U_{0,\lambda }^{(n)}$
with
$U_0^{(n)}=\cup _{\lambda } U_{0,\lambda }^{(n)}$
with
 $\lambda =\lambda _0+\lambda _1p+\ldots +\lambda _{n-1}p^{n-1}$
, where
$\lambda =\lambda _0+\lambda _1p+\ldots +\lambda _{n-1}p^{n-1}$
, where
 $\lambda _0,\lambda _1,\ldots ,\lambda _{n-1}\in \{0,1,\ldots ,p-1\}$
and we have
$\lambda _0,\lambda _1,\ldots ,\lambda _{n-1}\in \{0,1,\ldots ,p-1\}$
and we have
 $\displaystyle U_{0,\lambda }^{(n)}:={\mathbb P}^1\bigl ( \frac {T-\lambda }{p^n} \bigr )$
.
$\displaystyle U_{0,\lambda }^{(n)}:={\mathbb P}^1\bigl ( \frac {T-\lambda }{p^n} \bigr )$
.
We remark that for every
![]() $n\ge 1$
we have
$n\ge 1$
we have
![]() ${\mathbb P}^1({\mathbb Q}_p, {\mathbb Z}_p)\subset U_{\infty }^{(n)}\cup U_0^{(n)}$
, and moreover, the family
${\mathbb P}^1({\mathbb Q}_p, {\mathbb Z}_p)\subset U_{\infty }^{(n)}\cup U_0^{(n)}$
, and moreover, the family
![]() $\{U_{\infty }^{(n)}\cup U_0^{(n)}\}_{n\ge 1}$
is a fundamental system of open neighbourhoods of
$\{U_{\infty }^{(n)}\cup U_0^{(n)}\}_{n\ge 1}$
is a fundamental system of open neighbourhoods of
![]() ${\mathbb P}^1({\mathbb Q}_p,{\mathbb Z}_p)$
in
${\mathbb P}^1({\mathbb Q}_p,{\mathbb Z}_p)$
in
![]() ${\mathbb P}^1$
.
${\mathbb P}^1$
.
We recall from [Reference Scholze23, Thm. 3.3.18] that for every rational open subset
![]() $U'\subset U_0$
or
$U'\subset U_0$
or
![]() $U'\subset U_{\infty }$
the inverse image
$U'\subset U_{\infty }$
the inverse image
![]() ${\cal U}':=\pi _{\mathrm {HT}}^{-1}\bigl (U'\bigr )$
is an affinoid perfectoid open subspace of
${\cal U}':=\pi _{\mathrm {HT}}^{-1}\bigl (U'\bigr )$
is an affinoid perfectoid open subspace of
![]() $\mathcal {X}(p^{\infty },N)$
. In particular, it is quasi-compact so that it is also the inverse image of an open
$\mathcal {X}(p^{\infty },N)$
. In particular, it is quasi-compact so that it is also the inverse image of an open
![]() ${\cal U}^{\prime }_r$
via
${\cal U}^{\prime }_r$
via
![]() $\pi _r$
of
$\pi _r$
of
![]() $ \mathcal {X}(p^r,N)$
for some r using the homeomorphism
$ \mathcal {X}(p^r,N)$
for some r using the homeomorphism
![]() $\vert \mathcal {X}(p^{\infty },N) \vert \cong \displaystyle {\lim _{\infty \leftarrow n}} \vert \mathcal {X}(p^r,N) \vert $
. As the transition maps in the inverse limit are finite and surjective,
$\vert \mathcal {X}(p^{\infty },N) \vert \cong \displaystyle {\lim _{\infty \leftarrow n}} \vert \mathcal {X}(p^r,N) \vert $
. As the transition maps in the inverse limit are finite and surjective,
![]() ${\cal U}^{\prime }_r$
is in fact the image of
${\cal U}^{\prime }_r$
is in fact the image of
![]() ${\cal U}'$
via
${\cal U}'$
via
![]() $\pi _r$
for r large enough. If
$\pi _r$
for r large enough. If
![]() $U'$
is further invariant for the action of the Iwahori subgroup
$U'$
is further invariant for the action of the Iwahori subgroup
![]() $\mathrm {Iw}_s\subset \mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
of matrices which are upper triangular modulo
$\mathrm {Iw}_s\subset \mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
of matrices which are upper triangular modulo
![]() $p^s$
, then also
$p^s$
, then also
![]() ${\cal U}'$
is
${\cal U}'$
is
![]() $\mathrm {Iw}_s$
-invariant as
$\mathrm {Iw}_s$
-invariant as
![]() $\pi _{\mathrm {HT}}$
is
$\pi _{\mathrm {HT}}$
is
![]() $\mathrm { Iw}_s$
-equivariant and
$\mathrm { Iw}_s$
-equivariant and
![]() ${\cal U}'$
is the inverse image of a unique open
${\cal U}'$
is the inverse image of a unique open
![]() ${\cal U}^{\prime }_{0,s}$
of
${\cal U}^{\prime }_{0,s}$
of
![]() $ \mathcal {X}_0(p^s,N)$
. Indeed, given
$ \mathcal {X}_0(p^s,N)$
. Indeed, given
![]() ${\cal U}^{\prime }_r \subset \mathcal {X}(p^r,N)$
for some
${\cal U}^{\prime }_r \subset \mathcal {X}(p^r,N)$
for some
![]() $r\geq s$
such that its inverse image gives
$r\geq s$
such that its inverse image gives
![]() ${\cal U}'$
, then
${\cal U}'$
, then
![]() ${\cal U}^{\prime }_r$
is
${\cal U}^{\prime }_r$
is
![]() $\mathrm { Iw}_s$
-invariant. As the morphism
$\mathrm { Iw}_s$
-invariant. As the morphism
![]() $\mathcal {X}(p^r,N) \to \mathcal {X}_0(p^s,N) $
is finite Kummer étale and Galois with group
$\mathcal {X}(p^r,N) \to \mathcal {X}_0(p^s,N) $
is finite Kummer étale and Galois with group
![]() $G_s$
equal to the image of
$G_s$
equal to the image of
![]() $\mathrm {Iw}_s\subset \mathrm {\mathbf {GL}}_2({\mathbb Z}_p)\to \mathrm {\mathbf {GL}}_2({\mathbb Z}/p^r{\mathbb Z})$
then
$\mathrm {Iw}_s\subset \mathrm {\mathbf {GL}}_2({\mathbb Z}_p)\to \mathrm {\mathbf {GL}}_2({\mathbb Z}/p^r{\mathbb Z})$
then
![]() ${\cal U}^{\prime }_{0,s}:={\cal U}^{\prime }_r/G_s$
is an open of
${\cal U}^{\prime }_{0,s}:={\cal U}^{\prime }_r/G_s$
is an open of
![]() $ \mathcal {X}_0(p^s,N) $
with the required properties. Furthermore,
$ \mathcal {X}_0(p^s,N) $
with the required properties. Furthermore,
![]() ${\cal U}^{\prime }_{0,s}$
defines the open
${\cal U}^{\prime }_{0,s}$
defines the open
![]() $({\cal U}^{\prime }_r)_{r\geq s}$
for the pro-Kummer étale site of
$({\cal U}^{\prime }_r)_{r\geq s}$
for the pro-Kummer étale site of
![]() $ \mathcal {X}_0(p^s,N)$
, and hence of
$ \mathcal {X}_0(p^s,N)$
, and hence of
![]() $\mathcal {X}$
, given by
$\mathcal {X}$
, given by
![]() ${\cal U}^{\prime }_r:={\cal U}^{\prime }_{0,s} \times _{ \mathcal {X}_0(p^s,N)} \mathcal {X}(p^r,N)$
. By construction,
${\cal U}^{\prime }_r:={\cal U}^{\prime }_{0,s} \times _{ \mathcal {X}_0(p^s,N)} \mathcal {X}(p^r,N)$
. By construction,
![]() ${\cal U}'\sim \displaystyle {\lim _{\infty \leftarrow r}} {\cal U}^{\prime }_r$
.
${\cal U}'\sim \displaystyle {\lim _{\infty \leftarrow r}} {\cal U}^{\prime }_r$
.
In particular, for every
![]() $n\ge 1$
, we consider the open rational subspaces
$n\ge 1$
, we consider the open rational subspaces
![]() $U_{\infty }^{(n)}$
of
$U_{\infty }^{(n)}$
of
![]() $U_{\infty }$
and
$U_{\infty }$
and
![]() $U_0^{(n)}$
of
$U_0^{(n)}$
of
![]() $U_0$
defined above. We remark that
$U_0$
defined above. We remark that
![]() $U_{\infty }^{(n)}$
is invariant under the left action of the subgroup
$U_{\infty }^{(n)}$
is invariant under the left action of the subgroup
![]() $\mathrm {Iw}_n$
. Then we denote by
$\mathrm {Iw}_n$
. Then we denote by
![]() $\mathcal {X}(p^{\infty },N)_0^{(n)}:=\pi _{\mathrm {HT}}^{-1}\bigl (U_0^{(n)} \bigr ) $
and
$\mathcal {X}(p^{\infty },N)_0^{(n)}:=\pi _{\mathrm {HT}}^{-1}\bigl (U_0^{(n)} \bigr ) $
and
![]() $\mathcal {X}(p^{\infty },N)_{\infty }^{(n)}:=\pi _{\mathrm {HT}}^{-1}\bigl (U_{\infty }^{(n)} \bigr ) $
and recall that they define affinoid perfectoid open subspaces of
$\mathcal {X}(p^{\infty },N)_{\infty }^{(n)}:=\pi _{\mathrm {HT}}^{-1}\bigl (U_{\infty }^{(n)} \bigr ) $
and recall that they define affinoid perfectoid open subspaces of
![]() $ \mathcal {X}(p^{\infty },N)$
.
$ \mathcal {X}(p^{\infty },N)$
.
As explained above, they also define opens for the pro-Kummer étale site of
![]() $ \mathcal {X}_0(p^n,N)$
and of
$ \mathcal {X}_0(p^n,N)$
and of
![]() $\mathcal {X}$
respectively. Namely, for
$\mathcal {X}$
respectively. Namely, for
![]() $n\ge 1$
,
$n\ge 1$
,
![]() $\mathcal {X}(p^{\infty }, N)_{\infty }^{(n)}$
, being invariant under
$\mathcal {X}(p^{\infty }, N)_{\infty }^{(n)}$
, being invariant under
![]() $\mathrm {Iw}_n$
, descends to an affinoid open denoted
$\mathrm {Iw}_n$
, descends to an affinoid open denoted
![]() $\mathcal {X}_0(p^m, N)_{\infty }^{(n)}$
of
$\mathcal {X}_0(p^m, N)_{\infty }^{(n)}$
of
![]() $\mathcal {X}_0(p^m, N)$
, for all
$\mathcal {X}_0(p^m, N)$
, for all
![]() $m\ge n$
. We also have variants
$m\ge n$
. We also have variants
![]() $\mathcal {X}_1(p^m, N)_{\infty }^{(n)}$
, resp.
$\mathcal {X}_1(p^m, N)_{\infty }^{(n)}$
, resp.
![]() $\mathcal {X}(p^m, N)_{\infty }^{(n)}$
, if we descend to
$\mathcal {X}(p^m, N)_{\infty }^{(n)}$
, if we descend to
![]() $\mathcal {X}_1(p^m, N)$
, resp.
$\mathcal {X}_1(p^m, N)$
, resp.
![]() $\mathcal {X}(p^m, N)$
.
$\mathcal {X}(p^m, N)$
.
In contrast, as
![]() $U_0^{(n)}$
is invariant with respect to
$U_0^{(n)}$
is invariant with respect to
![]() $\mathrm {Iw}_1$
, the open
$\mathrm {Iw}_1$
, the open
![]() $\mathcal {X}(p^{\infty }, N)_0^{(n)}$
descends to an open affinoid denoted
$\mathcal {X}(p^{\infty }, N)_0^{(n)}$
descends to an open affinoid denoted
![]() $\mathcal {X}_0(p^m, N)_0^{(n)}$
of
$\mathcal {X}_0(p^m, N)_0^{(n)}$
of
![]() $\mathcal {X}_0(p^m, N)$
, for all
$\mathcal {X}_0(p^m, N)$
, for all
![]() $m\ge 1$
. In this case, we consider the variant
$m\ge 1$
. In this case, we consider the variant
![]() $\mathcal {X}(p^m, N)_0^{(n)}$
open of
$\mathcal {X}(p^m, N)_0^{(n)}$
open of
![]() $\mathcal {X}(p^m, N)$
.
$\mathcal {X}(p^m, N)$
.
Lemma 4.3. For every
![]() $h\in {\mathbb N}$
, there exists
$h\in {\mathbb N}$
, there exists
![]() $n=n(h)\geq 1$
such that for every
$n=n(h)\geq 1$
such that for every
![]() $r\geq n$
the universal elliptic curve over
$r\geq n$
the universal elliptic curve over
![]() $\mathcal {X}_0(p^r,N)_0^{(n)}$
and
$\mathcal {X}_0(p^r,N)_0^{(n)}$
and
![]() $\mathcal {X}_0(p^r,N)_{\infty }^{(n)}$
resp. admits a canonical subgroup of order
$\mathcal {X}_0(p^r,N)_{\infty }^{(n)}$
resp. admits a canonical subgroup of order
![]() $p^h$
.
$p^h$
.
Proof. This follows from [Reference Scholze23, Lemma 3.3.14], stating that the preimage via
![]() $\pi _{\mathrm {HT}}$
of
$\pi _{\mathrm {HT}}$
of
![]() ${\mathbb P}^1({\mathbb Q}_p, {\mathbb Z}_p)$
is, as a topological space, the closure of the inverse image in
${\mathbb P}^1({\mathbb Q}_p, {\mathbb Z}_p)$
is, as a topological space, the closure of the inverse image in
![]() $\mathcal {X}(p^{\infty },N)$
of the ordinary locus and the cusps of
$\mathcal {X}(p^{\infty },N)$
of the ordinary locus and the cusps of
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
In particular,
![]() $\mathcal {X}(p^{\infty },N)_0^{(n)}$
and
$\mathcal {X}(p^{\infty },N)_0^{(n)}$
and
![]() $ \mathcal {X}(p^{\infty },N)_{\infty }^{(n)}$
define a fundamental system of open neighbourhoods of the ordinary locus in
$ \mathcal {X}(p^{\infty },N)_{\infty }^{(n)}$
define a fundamental system of open neighbourhoods of the ordinary locus in
![]() $\mathcal {X}(p^{\infty },N)$
.
$\mathcal {X}(p^{\infty },N)$
.
Remark 4.4. Recall that the ordinary locus in
![]() $ \mathcal {X}_0(p,N)$
has two connected components. Then
$ \mathcal {X}_0(p,N)$
has two connected components. Then
![]() $\mathcal {X}(p,N)_0^{(1)}$
and
$\mathcal {X}(p,N)_0^{(1)}$
and
![]() $\mathcal {X}(p,N)_{\infty }^{(1)}$
are neighbourhoods of these two components. The first is defined by requiring that the level subgroup is not the canonical one while the second is the component where the level subgroup coincides with the canonical one. Following conventions going back to Robert Coleman, we set up the notation so that the first is indexed by
$\mathcal {X}(p,N)_{\infty }^{(1)}$
are neighbourhoods of these two components. The first is defined by requiring that the level subgroup is not the canonical one while the second is the component where the level subgroup coincides with the canonical one. Following conventions going back to Robert Coleman, we set up the notation so that the first is indexed by
![]() $0$
and the second by
$0$
and the second by
![]() $\infty $
.
$\infty $
.
A reason to introduce the open subsets
![]() $\mathcal {X}_0(p^r,N)_{\infty }^{(n)}$
for
$\mathcal {X}_0(p^r,N)_{\infty }^{(n)}$
for
![]() $r\ge n$
and
$r\ge n$
and
![]() $\mathcal {X}_0(p^r,N)_0^{(n)}$
, for any
$\mathcal {X}_0(p^r,N)_0^{(n)}$
, for any
![]() $r \geq 1$
, is that they behave nicely under the
$r \geq 1$
, is that they behave nicely under the
![]() $U_p$
-correspondence, as we will explain below.
$U_p$
-correspondence, as we will explain below.
4.3 On the Hodge–Tate period map
Over
![]() $\mathcal {X}(p^{\infty },N)$
, the sheaf
$\mathcal {X}(p^{\infty },N)$
, the sheaf
![]() $T_p(E)$
admits a universal trivialization
$T_p(E)$
admits a universal trivialization
The map
![]() $\mathrm {dlog}$
defines a surjective map onto the sheaf of invariant differentials of E
$\mathrm {dlog}$
defines a surjective map onto the sheaf of invariant differentials of E
which is used to define the map
![]() $\pi _{\mathrm {HT}}$
: For every log affinoid perfectoid open
$\pi _{\mathrm {HT}}$
: For every log affinoid perfectoid open
![]() $W\,{=}\,\mathrm {Spa}(R,R^+)$
of
$W\,{=}\,\mathrm {Spa}(R,R^+)$
of
![]() $\mathcal {X}(p^{\infty },N)$
such that the universal elliptic curve extends to a (generalized) elliptic curve over
$\mathcal {X}(p^{\infty },N)$
such that the universal elliptic curve extends to a (generalized) elliptic curve over
![]() $\mbox {Spec} (R^+)$
and
$\mbox {Spec} (R^+)$
and
![]() $\omega _E$
is generated as
$\omega _E$
is generated as
![]() $R^+$
-module by one element that we denote
$R^+$
-module by one element that we denote
![]() $\Omega _W$
, we write
$\Omega _W$
, we write
![]() $\mathrm {dlog}(a^{\vee })= \alpha \Omega _W$
,
$\mathrm {dlog}(a^{\vee })= \alpha \Omega _W$
,
![]() $\mathrm {dlog}(b^{\vee })= \beta \Omega _W$
with
$\mathrm {dlog}(b^{\vee })= \beta \Omega _W$
with
![]() $\alpha $
,
$\alpha $
,
![]() $\beta \in R$
generating the whole ring R. Then
$\beta \in R$
generating the whole ring R. Then
![]() $\pi _{\mathrm {HT}}\vert _W\colon W \to \mathbb {P}^1$
is defined in homogeneous coordinates by
$\pi _{\mathrm {HT}}\vert _W\colon W \to \mathbb {P}^1$
is defined in homogeneous coordinates by
![]() $[\alpha ;\beta ]$
. Namely, let
$[\alpha ;\beta ]$
. Namely, let
![]() $W_{\infty }\subset W$
be the rational open defined by
$W_{\infty }\subset W$
be the rational open defined by
![]() $W(1/\alpha )$
, and let
$W(1/\alpha )$
, and let
![]() $W_0\subset W$
be the rational open defined by
$W_0\subset W$
be the rational open defined by
![]() $W(1/\beta )$
. Then
$W(1/\beta )$
. Then
![]() $\pi _{\mathrm {HT}}\vert _{W_0}\colon W_0\to U_0$
sends the standard coordinate T on the standard affinoid neighbourhood
$\pi _{\mathrm {HT}}\vert _{W_0}\colon W_0\to U_0$
sends the standard coordinate T on the standard affinoid neighbourhood
![]() $U_0=\mathbb {A}^1$
of
$U_0=\mathbb {A}^1$
of
![]() $0$
to
$0$
to
![]() $\alpha /\beta $
and
$\alpha /\beta $
and
![]() $\pi _{\mathrm {HT}}\vert _{W_{\infty }}\colon W_{\infty }\to U_{\infty }$
sends the standard coordinate T on the standard affinoid neighbourhood
$\pi _{\mathrm {HT}}\vert _{W_{\infty }}\colon W_{\infty }\to U_{\infty }$
sends the standard coordinate T on the standard affinoid neighbourhood
![]() $U_{\infty }:=\mathbb {A}^1$
of
$U_{\infty }:=\mathbb {A}^1$
of
![]() $\infty $
to
$\infty $
to
![]() $\beta /\alpha $
.
$\beta /\alpha $
.
For every
![]() $n\in {\mathbb N}$
, we can refine such morphism to a morphism on
$n\in {\mathbb N}$
, we can refine such morphism to a morphism on
![]() $\mathcal {X}_0(p^n,N)_{\mathrm {pke}}$
as follows. Considering the smooth formal model
$\mathcal {X}_0(p^n,N)_{\mathrm {pke}}$
as follows. Considering the smooth formal model
![]() $\mathfrak {X}$
of the modular curve X over
$\mathfrak {X}$
of the modular curve X over
![]() ${\cal O}_{{\mathbb C}_p}$
given by moduli theory and the universal generalised elliptic curve E over
${\cal O}_{{\mathbb C}_p}$
given by moduli theory and the universal generalised elliptic curve E over
![]() $\mathfrak {X}$
, the invariant differentials of E relative to
$\mathfrak {X}$
, the invariant differentials of E relative to
![]() $\mathfrak {X}$
and the fact that
$\mathfrak {X}$
and the fact that
![]() $\mathcal {X}$
is the adic generic fibre of
$\mathcal {X}$
is the adic generic fibre of
![]() $\mathfrak {X}$
, give an invertible
$\mathfrak {X}$
, give an invertible
![]() ${\cal O}_{\mathcal {X}}^+$
-module
${\cal O}_{\mathcal {X}}^+$
-module
![]() $\omega _E^+$
on
$\omega _E^+$
on
![]() $\mathcal {X}$
. Pulling back via the projection map
$\mathcal {X}$
. Pulling back via the projection map
![]() $\mathcal {X}_0(p^n,N) \to \mathcal {X} $
, we get a
$\mathcal {X}_0(p^n,N) \to \mathcal {X} $
, we get a
![]() ${\cal O}_{\mathcal {X}_0(p^n,N)_{\mathrm {pke}}}^+$
-module for the pro-Kummer étale topology that we still abusively denote
${\cal O}_{\mathcal {X}_0(p^n,N)_{\mathrm {pke}}}^+$
-module for the pro-Kummer étale topology that we still abusively denote
![]() $\omega _E^+$
and passing to p-adic completions we finally obtain an invertible
$\omega _E^+$
and passing to p-adic completions we finally obtain an invertible
![]() $\widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)}^+$
-module
$\widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)}^+$
-module
![]() $ \widehat { \omega }_E^+$
. Here, for simplicity, we write
$ \widehat { \omega }_E^+$
. Here, for simplicity, we write
![]() $\widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)}^+$
for
$\widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)}^+$
for
![]() $\widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_{\mathrm {pke}}}^+$
.
$\widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_{\mathrm {pke}}}^+$
.
Consider the map
![]() $\mathrm {dlog}$
for the basis of
$\mathrm {dlog}$
for the basis of
![]() $\mathcal {X}_0(p^n,N)_{\mathrm {pke}}$
given in Lemma 4.1. Let a modulo
$\mathcal {X}_0(p^n,N)_{\mathrm {pke}}$
given in Lemma 4.1. Let a modulo
![]() $p^n$
be a generator in
$p^n$
be a generator in
![]() $T_ p(E)/ p^n T_p(E)$
of the level subgroup of order
$T_ p(E)/ p^n T_p(E)$
of the level subgroup of order
![]() $p^n$
. For every log affinoid perfectoid open U as in loc. cit., write
$p^n$
. For every log affinoid perfectoid open U as in loc. cit., write
![]() $\widehat {U}=\mathrm {Spa}(R,R^+)$
. Then
$\widehat {U}=\mathrm {Spa}(R,R^+)$
. Then
![]() $T_p(E)^{\vee }$
is constant on U; we have a universal generalized elliptic curve E over
$T_p(E)^{\vee }$
is constant on U; we have a universal generalized elliptic curve E over
![]() $\mbox {Spec}(R^+)$
and
$\mbox {Spec}(R^+)$
and
![]() $\widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)}^+(U)=R^+$
. We then have the map
$\widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)}^+(U)=R^+$
. We then have the map
![]() $\mathrm {dlog}\colon T_p(E)^{\vee }(U) \otimes _{{\mathbb Z}_p} R^+ \longrightarrow \widehat { \omega }_E^+(U)$
. Gluing, we obtain a map of sheaves on
$\mathrm {dlog}\colon T_p(E)^{\vee }(U) \otimes _{{\mathbb Z}_p} R^+ \longrightarrow \widehat { \omega }_E^+(U)$
. Gluing, we obtain a map of sheaves on
![]() $\mathcal {X}_0(p^n,N)_{\mathrm {pke}}$
:
$\mathcal {X}_0(p^n,N)_{\mathrm {pke}}$
:
Proposition 4.5. For every
![]() $r\in {\mathbb N}$
there exist
$r\in {\mathbb N}$
there exist
![]() $m\in N$
such that for every
$m\in N$
such that for every
![]() $n\in {\mathbb N}$
with
$n\in {\mathbb N}$
with
![]() $n\geq m$
, r the following hold:
$n\geq m$
, r the following hold:
-
a. There exists a canonical subgroup
 $C_r$
of order
$C_r$
of order
 $p^r$
on
$p^r$
on
 $\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
and on
$\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
and on
 $\mathcal {X}_0(p^n,N)_0^{(m)}$
which on
$\mathcal {X}_0(p^n,N)_0^{(m)}$
which on
 $\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
coincides with
$\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
coincides with
 $p^r$
-torsion of the level
$p^r$
-torsion of the level
 $p^n$
subgroup and which on
$p^n$
subgroup and which on
 $\mathcal {X}_0(p^n,N)_0^{(m)}$
is disjoint from the level
$\mathcal {X}_0(p^n,N)_0^{(m)}$
is disjoint from the level
 $p^n$
subgroup;
$p^n$
subgroup; -
b. There exists an invertible
 ${\cal O}_{\mathcal {X}_0(p^n,N)_{\infty }^{(m)}}^+$
-module
${\cal O}_{\mathcal {X}_0(p^n,N)_{\infty }^{(m)}}^+$
-module
 $\omega _E^{\mathrm {mod}}$
on
$\omega _E^{\mathrm {mod}}$
on
 $\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
(resp. a
$\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
(resp. a
 ${\cal O}_{\mathcal {X}_0(p^n,N)_0^{(m)}}^+$
-module
${\cal O}_{\mathcal {X}_0(p^n,N)_0^{(m)}}^+$
-module
 $\omega _E^{\mathrm {mod}}$
on
$\omega _E^{\mathrm {mod}}$
on
 $\mathcal {X}_0(p^n,N)_0^{(m)}$
) contained in
$\mathcal {X}_0(p^n,N)_0^{(m)}$
) contained in
 $\omega _E^+$
;
$\omega _E^+$
; -
c. The morphism
 $\mathrm {dlog}$
surjects onto the p-adic completion
$\mathrm {dlog}$
surjects onto the p-adic completion
 $\widehat {\omega }_E^{\mathrm {mod}}$
of the pullback of
$\widehat {\omega }_E^{\mathrm {mod}}$
of the pullback of
 $\omega _E^{\mathrm { mod}}$
to
$\omega _E^{\mathrm { mod}}$
to
 $\mathcal {X}_1(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}$
and its restriction to
$\mathcal {X}_1(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}$
and its restriction to
 $T_p(E)^{\vee }$
modulo
$T_p(E)^{\vee }$
modulo
 $p^r$
factors via
$p^r$
factors via
 $C_r^{\vee }$
. The kernel of
$C_r^{\vee }$
. The kernel of
 $\mathrm {dlog}$
is isomorphic to the p-adic completion of
$\mathrm {dlog}$
is isomorphic to the p-adic completion of
 $\bigl (\widehat {\omega }_E^{\mathrm {mod}}\bigr )^{-1}$
(here, we omit the Tate twist that usually appears as we work over
$\bigl (\widehat {\omega }_E^{\mathrm {mod}}\bigr )^{-1}$
(here, we omit the Tate twist that usually appears as we work over
 ${\mathbb C}_p$
);
${\mathbb C}_p$
); -
d. The map
 $\mathrm {dlog}$
surjects onto the p-adic completion
$\mathrm {dlog}$
surjects onto the p-adic completion
 $\widehat {\omega }_E^{\mathrm {mod}}$
of
$\widehat {\omega }_E^{\mathrm {mod}}$
of
 $\omega _E^{\mathrm {mod}}$
on
$\omega _E^{\mathrm {mod}}$
on
 $\mathcal {X}(p^n,N)_{0,{\mathrm {pke}}}^{(m)}$
and its restriction to
$\mathcal {X}(p^n,N)_{0,{\mathrm {pke}}}^{(m)}$
and its restriction to
 $T_p(E)^{\vee }$
modulo
$T_p(E)^{\vee }$
modulo
 $p^r$
factors via
$p^r$
factors via
 $C_r^{\vee }$
. The kernel of
$C_r^{\vee }$
. The kernel of
 $\mathrm {dlog}$
is isomorphic to the p-adic completion of
$\mathrm {dlog}$
is isomorphic to the p-adic completion of
 $\bigl (\widehat {\omega }_E^{\mathrm {mod}}\bigr )^{-1}$
.
$\bigl (\widehat {\omega }_E^{\mathrm {mod}}\bigr )^{-1}$
.
Proof. It follows from [Reference Andreatta, Iovita and Pilloni3] that the result holds true on strict neighbourhoods
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
of the ordinary loci in
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
of the ordinary loci in
![]() $\mathcal {X}$
defined by the points x, where
$\mathcal {X}$
defined by the points x, where
![]() $\vert p \vert _x < \vert \mathrm {Ha}^{p^s} \vert _x$
for s large enough; here,
$\vert p \vert _x < \vert \mathrm {Ha}^{p^s} \vert _x$
for s large enough; here,
![]() $\mathrm {Ha}$
is a (any) local lift of the Hasse invariant. Thanks to [Reference Scholze23, Lemma 3.3.8], there exists
$\mathrm {Ha}$
is a (any) local lift of the Hasse invariant. Thanks to [Reference Scholze23, Lemma 3.3.8], there exists
![]() $m\in {\mathbb N}$
such that
$m\in {\mathbb N}$
such that
![]() $\mathcal {X}(p^n,N)_{\infty }^{(m)}$
and
$\mathcal {X}(p^n,N)_{\infty }^{(m)}$
and
![]() $\mathcal {X}(p^n,N)_0^{(m)}$
are contained in
$\mathcal {X}(p^n,N)_0^{(m)}$
are contained in
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
. See Lemma 4.3. The claim follows.
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
. See Lemma 4.3. The claim follows.
Remark 4.6. See [Reference Chojecki, Hansen and Johansson12] for similar results in the case of Shimura curves. The notation
![]() $\omega _E^{\mathrm {mod}}$
is taken from [Reference Pilloni and Stroh20].
$\omega _E^{\mathrm {mod}}$
is taken from [Reference Pilloni and Stroh20].
From Proposition 4.5, we get an integral version of the Hodge–Tate exact sequence:
This will be useful to compute the cohomology
![]() $\mathrm {H}^1\bigl (\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}, \widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_{\infty }^{(n)}} \bigr )$
. In fact, tensoring the exact sequence with
$\mathrm {H}^1\bigl (\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}, \widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_{\infty }^{(n)}} \bigr )$
. In fact, tensoring the exact sequence with
![]() $\widehat {\omega }_E^{\mathrm {mod,2}}$
and taking the long exact sequence in cohomology we obtain a map
$\widehat {\omega }_E^{\mathrm {mod,2}}$
and taking the long exact sequence in cohomology we obtain a map
and similarly for
![]() $\mathcal {X}_0(p^n,N)_0^{(m)}$
, or their covers
$\mathcal {X}_0(p^n,N)_0^{(m)}$
, or their covers
![]() $\mathcal {X}_1(p^n,N)_{\infty }^{(m)}$
,
$\mathcal {X}_1(p^n,N)_{\infty }^{(m)}$
,
![]() $\mathcal {X}(p^n,N)_0^{(m)}$
.
$\mathcal {X}(p^n,N)_0^{(m)}$
.
4.4 The sheaf
 $\omega _E^k$
$\omega _E^k$
Take r, m and
![]() $n \in {\mathbb N}$
as in Proposition 4.5. The map
$n \in {\mathbb N}$
as in Proposition 4.5. The map
![]() $\mathrm {dlog}$
provides
$\mathrm {dlog}$
provides
![]() $\omega _E^{\mathrm {mod}}/p^r \omega _E^{\mathrm {mod}} $
with a marked section s over
$\omega _E^{\mathrm {mod}}/p^r \omega _E^{\mathrm {mod}} $
with a marked section s over
![]() $\mathcal {X}_1(p^n,N)_{\infty }^{(m)}$
as the image of the tautological generator of
$\mathcal {X}_1(p^n,N)_{\infty }^{(m)}$
as the image of the tautological generator of
![]() $C_r^{\vee }$
.
$C_r^{\vee }$
.
Similarly, recall that we have a decomposition
![]() $\mathcal {X}(p^n,N)_0^{(m)}=\amalg _{\lambda \in {\mathbb Z}/p^n{\mathbb Z}} \mathcal {X}(p^n,N)_{0,\lambda }^{(m)}$
, where over
$\mathcal {X}(p^n,N)_0^{(m)}=\amalg _{\lambda \in {\mathbb Z}/p^n{\mathbb Z}} \mathcal {X}(p^n,N)_{0,\lambda }^{(m)}$
, where over
![]() $\mathcal {X}(p^n,N)_{0,\lambda }^{(m)}$
, using the trivialization
$\mathcal {X}(p^n,N)_{0,\lambda }^{(m)}$
, using the trivialization
![]() $T_p(E)/p^n T_p(E)=({\mathbb Z}/p^n{\mathbb Z}) a \oplus ({\mathbb Z}/p^n{\mathbb Z}) b$
, we have
$T_p(E)/p^n T_p(E)=({\mathbb Z}/p^n{\mathbb Z}) a \oplus ({\mathbb Z}/p^n{\mathbb Z}) b$
, we have
![]() $\mathrm {dlog} (a^{\vee })=\lambda \mathrm {dlog} (b^{\vee })$
. In particular, the canonical subgroup
$\mathrm {dlog} (a^{\vee })=\lambda \mathrm {dlog} (b^{\vee })$
. In particular, the canonical subgroup
![]() $C_r$
is generated by
$C_r$
is generated by
![]() $b+\lambda a$
and
$b+\lambda a$
and
![]() $\omega _E^{\mathrm {mod}}/p^r \omega _E^{\mathrm {mod}} $
acquires a marked section
$\omega _E^{\mathrm {mod}}/p^r \omega _E^{\mathrm {mod}} $
acquires a marked section
![]() $s:=\mathrm { dlog} (b^{\vee })$
.
$s:=\mathrm { dlog} (b^{\vee })$
.
Suppose we are given an h-analytic character
![]() $k\colon {\mathbb Z}_p^{\ast } \to B^{\ast }$
, for
$k\colon {\mathbb Z}_p^{\ast } \to B^{\ast }$
, for
![]() $h\leq r$
, as in Definition 3.6. Using the formalism of VBMS from §3.3 for
$h\leq r$
, as in Definition 3.6. Using the formalism of VBMS from §3.3 for
![]() $\omega _E^{\mathrm {mod}}$
and the section s modulo
$\omega _E^{\mathrm {mod}}$
and the section s modulo
![]() $p^r$
, we get the invertible
$p^r$
, we get the invertible
![]() ${\cal O}_{\mathcal {X}_1(p^n,N)_{\infty }^{(m)}}^+\widehat {\otimes } B$
-module, resp.
${\cal O}_{\mathcal {X}_1(p^n,N)_{\infty }^{(m)}}^+\widehat {\otimes } B$
-module, resp.
![]() ${\cal O}_{\mathcal {X}(p^n,N)_0^{(m)}}\widehat {\otimes } B$
-module
${\cal O}_{\mathcal {X}(p^n,N)_0^{(m)}}\widehat {\otimes } B$
-module
Since
![]() $\omega _E^{\mathrm {mod}}$
and the section s modulo
$\omega _E^{\mathrm {mod}}$
and the section s modulo
![]() $p^r$
are stable under the action of the automorphism group
$p^r$
are stable under the action of the automorphism group
![]() $\Delta _n:=({\mathbb Z}/p^n{\mathbb Z})^{\ast }$
of
$\Delta _n:=({\mathbb Z}/p^n{\mathbb Z})^{\ast }$
of
![]() $j_n\colon \mathcal {X}_1(p^n,N)_{\infty }^{(m)}\to \mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
, then
$j_n\colon \mathcal {X}_1(p^n,N)_{\infty }^{(m)}\to \mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
, then
![]() $({\mathbb Z}/p^n{\mathbb Z})^{\ast }$
acts on
$({\mathbb Z}/p^n{\mathbb Z})^{\ast }$
acts on
![]() $j_{n,\ast }\bigl (\omega _E^k[1/p]\bigr )$
and, taking the subsheaf of
$j_{n,\ast }\bigl (\omega _E^k[1/p]\bigr )$
and, taking the subsheaf of
![]() $j_{n,\ast }\bigl (\omega _E^k[1/p]\bigr )$
on which
$j_{n,\ast }\bigl (\omega _E^k[1/p]\bigr )$
on which
![]() ${\mathbb Z}_p^{\ast }$
acts via the character k, then
${\mathbb Z}_p^{\ast }$
acts via the character k, then
![]() $j_{n,\ast }\bigl (\omega _E^k[1/p]\bigr )$
descends to an invertible
$j_{n,\ast }\bigl (\omega _E^k[1/p]\bigr )$
descends to an invertible
![]() ${\cal O}_{\mathcal {X}_0(p^n,N)_{\infty }^{(m)}}\widehat {\otimes } B[1/p]$
-module that we denote
${\cal O}_{\mathcal {X}_0(p^n,N)_{\infty }^{(m)}}\widehat {\otimes } B[1/p]$
-module that we denote
![]() $\omega _E^k[1/p] $
.
$\omega _E^k[1/p] $
.
Similarly, the Galois group of
![]() $j^{\prime }_n\colon \mathcal {X}(p^n,N)_0^{(m)}\to \mathcal {X}_0(p^n,N)_0^{(m)}$
, which is identified with the standard Borel subgroup of
$j^{\prime }_n\colon \mathcal {X}(p^n,N)_0^{(m)}\to \mathcal {X}_0(p^n,N)_0^{(m)}$
, which is identified with the standard Borel subgroup of
![]() $\mathrm {GL}_2({\mathbb Z}/p^n{\mathbb Z})$
, acts compatibly on
$\mathrm {GL}_2({\mathbb Z}/p^n{\mathbb Z})$
, acts compatibly on
![]() $(\omega _E^{\mathrm {mod}},s)$
and hence it acts on
$(\omega _E^{\mathrm {mod}},s)$
and hence it acts on
![]() $j^{\prime }_{n,\ast }\bigl (\omega _E^k[1/p]\bigr )$
. In this case we let
$j^{\prime }_{n,\ast }\bigl (\omega _E^k[1/p]\bigr )$
. In this case we let
![]() $\omega _E^k[1/p]$
be the invertible
$\omega _E^k[1/p]$
be the invertible
![]() ${\cal O}_{\mathcal {X}_0(p^n,N)_0^{(m)}}\widehat {\otimes } B[1/p]$
-module defined as the subsheaf of
${\cal O}_{\mathcal {X}_0(p^n,N)_0^{(m)}}\widehat {\otimes } B[1/p]$
-module defined as the subsheaf of
![]() $j^{\prime }_{n,\ast }\bigl (\omega _E^k[1/p]\bigr )$
on which the standard Borel subroup of
$j^{\prime }_{n,\ast }\bigl (\omega _E^k[1/p]\bigr )$
on which the standard Borel subroup of
![]() $\mathrm {GL}_2({\mathbb Z}_p)$
acts via the projection onto the lower right entry
$\mathrm {GL}_2({\mathbb Z}_p)$
acts via the projection onto the lower right entry
![]() ${\mathbb Z}_p^{\ast }$
composed with the character k.
${\mathbb Z}_p^{\ast }$
composed with the character k.
4.5 The
 $U_p$
-correspondence
$U_p$
-correspondence
Given the modular curve
![]() $\mathcal {X}_0(p^s,N)$
for
$\mathcal {X}_0(p^s,N)$
for
![]() $s\geq 1$
, we have correspondences
$s\geq 1$
, we have correspondences
![]() $T_{\ell }$
, for
$T_{\ell }$
, for
![]() $\ell $
not dividing
$\ell $
not dividing
![]() $p N$
, and
$p N$
, and
![]() $U_p$
. They are defined by the analytification
$U_p$
. They are defined by the analytification
![]() $\mathcal {X}_0(p^s,N, \ell )$
, resp.
$\mathcal {X}_0(p^s,N, \ell )$
, resp.
![]() $\mathcal {X}_0(p^s,N,p)$
, of the modular curve
$\mathcal {X}_0(p^s,N,p)$
, of the modular curve
![]() $X_0(p^s,N,\ell )$
, resp.
$X_0(p^s,N,\ell )$
, resp.
![]() $X_0(p^s,N,p) $
, classifying, at least away from the cusps, subgroups D of order
$X_0(p^s,N,p) $
, classifying, at least away from the cusps, subgroups D of order
![]() $\ell $
of the universal elliptic curve E, resp. subgroups of order p of E complementary to the p-torsion
$\ell $
of the universal elliptic curve E, resp. subgroups of order p of E complementary to the p-torsion
![]() $H_1$
of the cyclic subgroup
$H_1$
of the cyclic subgroup
![]() $H_s$
of order
$H_s$
of order
![]() $p^s$
defined by the level structure. We have two maps
$p^s$
defined by the level structure. We have two maps
![]() $q_1,q_2\colon ,\mathcal {X}_0(p^s,N, \ell ) \to \mathcal {X}_0(p^s,N)$
defined by the analytification of the maps
$q_1,q_2\colon ,\mathcal {X}_0(p^s,N, \ell ) \to \mathcal {X}_0(p^s,N)$
defined by the analytification of the maps
![]() $q_1,q_2\colon X_0(p^s,N,\ell )\to X_0(p^s,N) $
, where
$q_1,q_2\colon X_0(p^s,N,\ell )\to X_0(p^s,N) $
, where
![]() $q_1$
sends the universal object
$q_1$
sends the universal object
![]() $(E,H_s,\Psi _N,D)$
to
$(E,H_s,\Psi _N,D)$
to
![]() $(E,H_s,\Psi _N)$
(the forgetful map) and
$(E,H_s,\Psi _N)$
(the forgetful map) and
![]() $q_2$
sends the universal object
$q_2$
sends the universal object
![]() $(E,H_s,\Psi _N,D)$
to
$(E,H_s,\Psi _N,D)$
to
![]() $(E/D, H_s',\Psi _N')$
, where
$(E/D, H_s',\Psi _N')$
, where
![]() $H_s'$
is the image of
$H_s'$
is the image of
![]() $H_s$
via the isogeny
$H_s$
via the isogeny
![]() $E\to E/D$
and
$E\to E/D$
and
![]() $\Psi _N'$
is
$\Psi _N'$
is
![]() $\Psi _N$
composed with this isogeny.
$\Psi _N$
composed with this isogeny.
These maps induce morphisms of sites
![]() $\mathcal {X}_0(p^s,N,\ell )_{\mathrm {pke}} \to \mathcal {X}_0(p^s,N)_{\mathrm {pke}} $
, resp.
$\mathcal {X}_0(p^s,N,\ell )_{\mathrm {pke}} \to \mathcal {X}_0(p^s,N)_{\mathrm {pke}} $
, resp.
![]() $\mathcal {X}_0(p^s, N,p )_{\mathrm {pke}} \to \mathcal {X}_0(p^s,N)_{\mathrm {pke}} $
. As
$\mathcal {X}_0(p^s, N,p )_{\mathrm {pke}} \to \mathcal {X}_0(p^s,N)_{\mathrm {pke}} $
. As
![]() $q_1, q_2$
are finite Kummer étale, the following follows from the discussion in [Reference Andreatta, Iovita and Stevens5, Cor. 2.6] or [Reference Diao, Lan, Liu and Zhu15, Prop. 4.5.2].
$q_1, q_2$
are finite Kummer étale, the following follows from the discussion in [Reference Andreatta, Iovita and Stevens5, Cor. 2.6] or [Reference Diao, Lan, Liu and Zhu15, Prop. 4.5.2].
Lemma 4.7. There is a natural isomorphism of functors
![]() $q_{i,\ast }\cong q_{i,!}$
. In particular,
$q_{i,\ast }\cong q_{i,!}$
. In particular,
![]() $q_{i,\ast }$
is exact and we have a natural transformation
$q_{i,\ast }$
is exact and we have a natural transformation
![]() $\mathrm {Tr}_{q_i}\colon q_{i,\ast } q_i^{\ast } \to \mathrm {Id}$
, called the trace map.
$\mathrm {Tr}_{q_i}\colon q_{i,\ast } q_i^{\ast } \to \mathrm {Id}$
, called the trace map.
The maps
![]() $q_1$
and
$q_1$
and
![]() $q_2$
induce maps of perfectoid spaces. Take
$q_2$
induce maps of perfectoid spaces. Take
![]() $\ell $
prime to N but possibly equal to p. The fibre product
$\ell $
prime to N but possibly equal to p. The fibre product
![]() $\mathcal {X}(p^{\infty },N,\ell ):=\mathcal {X}(p^{\infty },N) \times _{\mathcal {X}_0(p^s,N)}^{q_i} \mathcal {X}_0(p^s,N,\ell )$
exists and is independent of the choice of maps
$\mathcal {X}(p^{\infty },N,\ell ):=\mathcal {X}(p^{\infty },N) \times _{\mathcal {X}_0(p^s,N)}^{q_i} \mathcal {X}_0(p^s,N,\ell )$
exists and is independent of the choice of maps
![]() $q_1$
or
$q_1$
or
![]() $q_2$
. We then have the two projections
$q_2$
. We then have the two projections
![]() $q_1,q_2\colon \mathcal {X}(p^{\infty },N,\ell ) \to \mathcal {X}(p^s,N)$
. Notice that
$q_1,q_2\colon \mathcal {X}(p^{\infty },N,\ell ) \to \mathcal {X}(p^s,N)$
. Notice that
![]() $\mathcal {X}(p^{\infty },N,p )$
splits completely as
$\mathcal {X}(p^{\infty },N,p )$
splits completely as
where over the copy labeled by
![]() $\lambda =0,\ldots ,p-1$
the isogeny
$\lambda =0,\ldots ,p-1$
the isogeny
![]() $E\to E':=E/D$
produces the map of
$E\to E':=E/D$
produces the map of
![]() ${\mathbb Z}_p$
-modules
${\mathbb Z}_p$
-modules
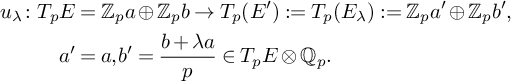 $$ \begin{align*} u_{\lambda} \colon T_p E&={\mathbb Z}_p a \oplus {\mathbb Z}_p b \to T_p(E'):=T_p(E_{\lambda}):={\mathbb Z}_p a' \oplus {\mathbb Z}_p b', \\ a'&=a, b'=\frac{b+\lambda a}{p}\in T_p E \otimes {\mathbb Q}_p. \end{align*} $$
$$ \begin{align*} u_{\lambda} \colon T_p E&={\mathbb Z}_p a \oplus {\mathbb Z}_p b \to T_p(E'):=T_p(E_{\lambda}):={\mathbb Z}_p a' \oplus {\mathbb Z}_p b', \\ a'&=a, b'=\frac{b+\lambda a}{p}\in T_p E \otimes {\mathbb Q}_p. \end{align*} $$
Using this description, the maps
![]() $q_1$
and
$q_1$
and
![]() $q_2$
restricted to the component labeled
$q_2$
restricted to the component labeled
![]() $\lambda $
define maps
$\lambda $
define maps
![]() $q_{1,\lambda }$
and
$q_{1,\lambda }$
and
![]() $q_{2,\lambda }$
, where
$q_{2,\lambda }$
, where
![]() $q_{1,\lambda }$
is the identity map and
$q_{1,\lambda }$
is the identity map and
![]() $q_{2,\lambda }\colon \mathcal {X}(p^{\infty },N) \to \mathcal {X}(p^{\infty },N) $
is an isomorphism such that the pullback of
$q_{2,\lambda }\colon \mathcal {X}(p^{\infty },N) \to \mathcal {X}(p^{\infty },N) $
is an isomorphism such that the pullback of
![]() $T_p E$
is
$T_p E$
is
![]() $T_p(E_{\lambda })$
.
$T_p(E_{\lambda })$
.
We consider the maps
![]() $t_1,t_2\colon \amalg _{\lambda =0,\ldots ,p-1} {\mathbb P}^1 \to {\mathbb P}^1$
where on the component labeled by
$t_1,t_2\colon \amalg _{\lambda =0,\ldots ,p-1} {\mathbb P}^1 \to {\mathbb P}^1$
where on the component labeled by
![]() $\lambda $
the map
$\lambda $
the map
![]() $t_{1,\lambda }$
induced by
$t_{1,\lambda }$
induced by
![]() $t_1$
is the identity while the map
$t_1$
is the identity while the map
![]() $t_2$
is the isomorphism
$t_2$
is the isomorphism
![]() $t_{2,\lambda }\colon {\mathbb P}^1 \to {\mathbb P}^1$
defined on points by
$t_{2,\lambda }\colon {\mathbb P}^1 \to {\mathbb P}^1$
defined on points by
![]() $[\alpha ,\beta ]\mapsto [\alpha - \lambda \beta ,p \beta ]$
. We then have the following diagram:
$[\alpha ,\beta ]\mapsto [\alpha - \lambda \beta ,p \beta ]$
. We then have the following diagram:
 $$ \begin{align*}\begin{matrix} \mathcal{X}(p^{\infty},N) & \stackrel{q_2}{\longleftarrow} & \mathcal{X}(p^{\infty},N,p )= \amalg_{\lambda=0,\ldots,p-1} \mathcal{X}(p^{\infty},N) & \stackrel{q_1}{\longrightarrow} & \mathcal{X}(p^{\infty},N) \cr \pi_{\mathrm{HT}} \big\downarrow & & \amalg_{\lambda=0,\ldots,p-1} \pi_{\mathrm{HT}} \big\downarrow & & \pi_{\mathrm{HT}} \big\downarrow\\ {\mathbb P}^1 & \stackrel{t_2}{\longleftarrow} & \amalg_{\lambda=0,\ldots,p-1} {\mathbb P}^1 & \stackrel{t_1}{\longrightarrow} & {\mathbb P}^1.\cr \end{matrix} \end{align*} $$
$$ \begin{align*}\begin{matrix} \mathcal{X}(p^{\infty},N) & \stackrel{q_2}{\longleftarrow} & \mathcal{X}(p^{\infty},N,p )= \amalg_{\lambda=0,\ldots,p-1} \mathcal{X}(p^{\infty},N) & \stackrel{q_1}{\longrightarrow} & \mathcal{X}(p^{\infty},N) \cr \pi_{\mathrm{HT}} \big\downarrow & & \amalg_{\lambda=0,\ldots,p-1} \pi_{\mathrm{HT}} \big\downarrow & & \pi_{\mathrm{HT}} \big\downarrow\\ {\mathbb P}^1 & \stackrel{t_2}{\longleftarrow} & \amalg_{\lambda=0,\ldots,p-1} {\mathbb P}^1 & \stackrel{t_1}{\longrightarrow} & {\mathbb P}^1.\cr \end{matrix} \end{align*} $$
In fact, the squares are commutative. This follows from the functoriality of
![]() $\mathrm {dlog}$
with respect to isogenies and by computing
$\mathrm {dlog}$
with respect to isogenies and by computing
![]() $u_{\lambda }^{\vee }$
: The map
$u_{\lambda }^{\vee }$
: The map
![]() $u_{\lambda }$
sends
$u_{\lambda }$
sends
![]() $a\mapsto a'$
and
$a\mapsto a'$
and
![]() $b\mapsto p b'-\lambda a'$
so that on the dual basis
$b\mapsto p b'-\lambda a'$
so that on the dual basis
![]() $u_{\lambda }^{\vee }$
sends
$u_{\lambda }^{\vee }$
sends
![]() $(a')^{\vee }\mapsto a^{\vee }-\lambda b^{\vee }$
and
$(a')^{\vee }\mapsto a^{\vee }-\lambda b^{\vee }$
and
![]() $(b')^{\vee }\mapsto p b^{\vee }$
.
$(b')^{\vee }\mapsto p b^{\vee }$
.
Remark 4.8. Let us observe that, with the notations above, if we denote by
![]() $U_p$
the correspondence on
$U_p$
the correspondence on
![]() $\mathcal {X}(p^{\infty },N)$
given by
$\mathcal {X}(p^{\infty },N)$
given by
![]() $U_p:=q_{2}\circ q_1^{-1}$
and if we denote by
$U_p:=q_{2}\circ q_1^{-1}$
and if we denote by
![]() $\widetilde {U}$
the correspondence on
$\widetilde {U}$
the correspondence on
![]() ${\mathbb P}^1$
defined by
${\mathbb P}^1$
defined by
![]() $\widetilde {U}:=t_{2}\circ t_1^{-1}$
, then we have:
$\widetilde {U}:=t_{2}\circ t_1^{-1}$
, then we have:
![]() $\pi _{\mathrm {HT}}\circ U_p=\widetilde {U}\circ \pi _{\mathrm {HT}}$
.
$\pi _{\mathrm {HT}}\circ U_p=\widetilde {U}\circ \pi _{\mathrm {HT}}$
.
We conclude this section with a lemma on the dynamic of the operators
![]() $t_{2,\lambda }$
. For
$t_{2,\lambda }$
. For
![]() $\lambda =0,\ldots ,p-1$
we write
$\lambda =0,\ldots ,p-1$
we write
![]() $t_{\lambda }$
in place of
$t_{\lambda }$
in place of
![]() $t_{2,\lambda }$
in the next lemma.
$t_{2,\lambda }$
in the next lemma.
Lemma 4.9.
a) Let
![]() $\lambda =\lambda _0 + p \lambda _1 + \cdots + \lambda _n p^n$
with
$\lambda =\lambda _0 + p \lambda _1 + \cdots + \lambda _n p^n$
with
![]() $\lambda _i\in \{0,\ldots , p-1\}$
. Write
$\lambda _i\in \{0,\ldots , p-1\}$
. Write
![]() $t_{\lambda }:=t_{\lambda _n} \circ \cdots \circ t_{\lambda _0}$
. Then
$t_{\lambda }:=t_{\lambda _n} \circ \cdots \circ t_{\lambda _0}$
. Then
![]() $t_{\lambda }\bigl (U_{0,\lambda }^{(n+1)}\bigr )= U_0$
,
$t_{\lambda }\bigl (U_{0,\lambda }^{(n+1)}\bigr )= U_0$
,
![]() $t_{\lambda }\bigl ({\mathbb P}^1\backslash U_{0,\lambda }^{(n+1)}\bigr )=U^{(1)}_{\infty }$
.
$t_{\lambda }\bigl ({\mathbb P}^1\backslash U_{0,\lambda }^{(n+1)}\bigr )=U^{(1)}_{\infty }$
.
b) If
![]() $\mu :=\lambda _0+\lambda _1p+\ldots +\lambda _{n-1}p^{n-1}$
with
$\mu :=\lambda _0+\lambda _1p+\ldots +\lambda _{n-1}p^{n-1}$
with
![]() $\lambda _i$
as above for
$\lambda _i$
as above for
![]() $0\le i\le n-1$
and
$0\le i\le n-1$
and
![]() $t_{\mu }:=t_{\lambda _{n-1}}\circ \ldots \circ t_{\lambda _0}$
, then we have
$t_{\mu }:=t_{\lambda _{n-1}}\circ \ldots \circ t_{\lambda _0}$
, then we have
![]() $t_{\mu }\bigl ({\mathbb P}^1\backslash U_{0,\lambda }^{(n+1)}\bigr ) \subset U_{\infty }\backslash U_0^{(1)}$
and
$t_{\mu }\bigl ({\mathbb P}^1\backslash U_{0,\lambda }^{(n+1)}\bigr ) \subset U_{\infty }\backslash U_0^{(1)}$
and
![]() $t_{\mu }(U_{\infty }^{(1)})\subset U_{\infty }^{(n+1)}$
.
$t_{\mu }(U_{\infty }^{(1)})\subset U_{\infty }^{(n+1)}$
.
Proof. It is enough to prove the statement for
![]() $\mathrm {Spa}(K,K^+)$
-valued points for an affinoid field
$\mathrm {Spa}(K,K^+)$
-valued points for an affinoid field
![]() $(K,K^+)$
. This is determined by a K-valued point of
$(K,K^+)$
. This is determined by a K-valued point of
![]() ${\mathbb P}^1$
, or equivalently a
${\mathbb P}^1$
, or equivalently a
![]() $K^+$
-valued point
$K^+$
-valued point
![]() $[\alpha ;\beta ]$
as
$[\alpha ;\beta ]$
as
![]() $K^+$
is a valuation ring, whose normalized valuation is denoted v.
$K^+$
is a valuation ring, whose normalized valuation is denoted v.
a) We prove the statement for
![]() $\lambda =\lambda _0$
leaving the inductive process to the reader. If
$\lambda =\lambda _0$
leaving the inductive process to the reader. If
![]() $[\alpha ;\beta ]$
is a point of
$[\alpha ;\beta ]$
is a point of
![]() $U_{\infty }\backslash U_0$
, then we can assume that
$U_{\infty }\backslash U_0$
, then we can assume that
![]() $\alpha =1$
and that
$\alpha =1$
and that
![]() $\beta $
is in the maximal ideal of
$\beta $
is in the maximal ideal of
![]() $K^+$
and
$K^+$
and
![]() $t_{\lambda }([1;\beta ])=[1-\lambda \beta; p \beta ]$
defines a point of
$t_{\lambda }([1;\beta ])=[1-\lambda \beta; p \beta ]$
defines a point of
![]() $U_{\infty }^{(1)}$
.
$U_{\infty }^{(1)}$
.
If
![]() $\beta $
is a unit, we can assume that
$\beta $
is a unit, we can assume that
![]() $\beta =1$
and then
$\beta =1$
and then
![]() $t_{\lambda }([\alpha ;1])=[\alpha -\lambda; p ]$
. This is a point of
$t_{\lambda }([\alpha ;1])=[\alpha -\lambda; p ]$
. This is a point of
![]() $U_0$
if and only if
$U_0$
if and only if
![]() $\frac {\alpha -\lambda }{p}\in K^+$
, that is, if and only if
$\frac {\alpha -\lambda }{p}\in K^+$
, that is, if and only if
![]() $[\alpha ;1]$
defines a point of
$[\alpha ;1]$
defines a point of
![]() $U_{0,\lambda }^{(1)}$
. Else
$U_{0,\lambda }^{(1)}$
. Else
![]() $\frac {p}{\alpha -\lambda }$
lies in the maximal ideal of
$\frac {p}{\alpha -\lambda }$
lies in the maximal ideal of
![]() $K^+$
and then
$K^+$
and then
![]() $t_{\lambda }([\alpha ;1])$
defines a point of
$t_{\lambda }([\alpha ;1])$
defines a point of
![]() $U_{\infty }\backslash U_0$
.
$U_{\infty }\backslash U_0$
.
b) If
![]() $[\alpha , \beta ]\in {\mathbb P}^1\backslash U_0^{(n+1)}$
,
$[\alpha , \beta ]\in {\mathbb P}^1\backslash U_0^{(n+1)}$
,
![]() $\alpha , \beta \in K^+$
, we may assume that one of
$\alpha , \beta \in K^+$
, we may assume that one of
![]() $\alpha , \beta $
is
$\alpha , \beta $
is
![]() $1$
.
$1$
.
If
![]() $\beta =1$
, we have
$\beta =1$
, we have
![]() $t_{\mu }([\alpha , 1])=[\alpha -\mu , p^n]$
. Moreover,
$t_{\mu }([\alpha , 1])=[\alpha -\mu , p^n]$
. Moreover,
![]() $[\alpha , 1]\notin U_0^{(n+1)}$
implies either that
$[\alpha , 1]\notin U_0^{(n+1)}$
implies either that
![]() $r:=v(\alpha -\mu )<n$
and in this case
$r:=v(\alpha -\mu )<n$
and in this case
![]() $[\alpha -\mu , p^n]\in U_{\infty }\backslash U_0^{(1)}$
, or that
$[\alpha -\mu , p^n]\in U_{\infty }\backslash U_0^{(1)}$
, or that
![]() $v(\alpha -\mu )=n$
and
$v(\alpha -\mu )=n$
and
![]() $\alpha =\mu +p^n\gamma $
, with
$\alpha =\mu +p^n\gamma $
, with
![]() $\gamma \in K^+$
,
$\gamma \in K^+$
,
![]() $\gamma \notin {\mathbb F}_p (\mathrm {mod }\ pK^+)$
. Then
$\gamma \notin {\mathbb F}_p (\mathrm {mod }\ pK^+)$
. Then
![]() $t_{\mu }([\alpha , \beta ])=[\gamma , 1]\in U_{\infty }\backslash U_0^{(1)}$
.
$t_{\mu }([\alpha , \beta ])=[\gamma , 1]\in U_{\infty }\backslash U_0^{(1)}$
.
If now
![]() $\alpha =1$
and
$\alpha =1$
and
![]() $\beta $
is in the maximal ideal of
$\beta $
is in the maximal ideal of
![]() $K^+$
, we have
$K^+$
, we have
![]() $t_{\mu }([1, \beta ])=[1-\mu \beta , p^n\beta ]$
. Since
$t_{\mu }([1, \beta ])=[1-\mu \beta , p^n\beta ]$
. Since
![]() $1-\mu \beta \in (K^+)^{\ast }$
, we have
$1-\mu \beta \in (K^+)^{\ast }$
, we have
![]() $t_{\mu }([1, \beta ])=[1, p^n\beta /(1-\mu \beta )]\in U_{\infty }^{(n)}\subset U_{\infty }\backslash U_0^{(1)}.$
$t_{\mu }([1, \beta ])=[1, p^n\beta /(1-\mu \beta )]\in U_{\infty }^{(n)}\subset U_{\infty }\backslash U_0^{(1)}.$
Let us notice that if
![]() $x\in U_{\infty }\backslash U_0^{(1)}$
and
$x\in U_{\infty }\backslash U_0^{(1)}$
and
![]() $\nu \in \{ 0,1,\ldots ,p-1\}$
, then
$\nu \in \{ 0,1,\ldots ,p-1\}$
, then
![]() $t_{\nu }(x)\in U_{\infty }^{(1)}$
. This observation and claim (b) imply the part
$t_{\nu }(x)\in U_{\infty }^{(1)}$
. This observation and claim (b) imply the part
![]() $t_{\lambda }({\mathbb P}^1\backslash U_0^{(n+1)})\subset U_{\infty }^{(1)}$
of claim (a).
$t_{\lambda }({\mathbb P}^1\backslash U_0^{(n+1)})\subset U_{\infty }^{(1)}$
of claim (a).
4.6 Étale sheaves
Let
![]() $H\subset \mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
be a finite index subgroup. In this section, we recall the tensor functor from the category of profinite H-representations to the category of sheaves on the pro-Kummer étale site of the modular curve
$H\subset \mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
be a finite index subgroup. In this section, we recall the tensor functor from the category of profinite H-representations to the category of sheaves on the pro-Kummer étale site of the modular curve
![]() $X(H,N)$
defined by H or, equivalently, of the associated adic space
$X(H,N)$
defined by H or, equivalently, of the associated adic space
![]() $\mathcal {X}(H,N)$
. We work with the latter.
$\mathcal {X}(H,N)$
. We work with the latter.
We fix log geometric points
![]() $\zeta _i$
, one for every connected component
$\zeta _i$
, one for every connected component
![]() $Z_i$
of
$Z_i$
of
![]() $\mathcal {X}(H,N)$
. Due to [Reference Diao, Lan, Liu and Zhu15, Prop. 5.1.12], the sites
$\mathcal {X}(H,N)$
. Due to [Reference Diao, Lan, Liu and Zhu15, Prop. 5.1.12], the sites
![]() $Z_{i,{\mathrm {fket}}}$
are Galois categories with underlying profinite group, the Kummer étale fundamental group
$Z_{i,{\mathrm {fket}}}$
are Galois categories with underlying profinite group, the Kummer étale fundamental group
![]() $\pi _1^{\mathrm {ket}}(Z_i,\zeta _i)$
. In particular, the pro-Kummer finite étale cover
$\pi _1^{\mathrm {ket}}(Z_i,\zeta _i)$
. In particular, the pro-Kummer finite étale cover
![]() $\bigl (\mathcal {X}(p^r,N)\bigr )_{r}$
of
$\bigl (\mathcal {X}(p^r,N)\bigr )_{r}$
of
![]() $\mathcal {X}(H,N)$
for r big enough, restricted to each
$\mathcal {X}(H,N)$
for r big enough, restricted to each
![]() $Z_i$
defines a homomorphism
$Z_i$
defines a homomorphism
Given a finite representation
![]() $L_n$
of H, we view it as a representation of
$L_n$
of H, we view it as a representation of
![]() $\pi _1(Z_i,\zeta _i)$
, for every i, and hence as a local system on each
$\pi _1(Z_i,\zeta _i)$
, for every i, and hence as a local system on each
![]() $Z_{i,{\mathrm {ket}}}$
and, hence, a local system
$Z_{i,{\mathrm {ket}}}$
and, hence, a local system
![]() $\mathbb {L}_n$
on
$\mathbb {L}_n$
on
![]() $\mathcal {X}(H,N)_{\mathrm {ket}}$
. In fact,
$\mathcal {X}(H,N)_{\mathrm {ket}}$
. In fact,
![]() $\mathbb {L}_n$
is a sheaf on
$\mathbb {L}_n$
is a sheaf on
![]() $\mathcal {X}(H,N)_{\mathrm {ket}}$
such that there exists a finite Kummer étale cover
$\mathcal {X}(H,N)_{\mathrm {ket}}$
such that there exists a finite Kummer étale cover
![]() $\mathcal {X}(p^r,N) \to \mathcal {X}(H,N)$
, for
$\mathcal {X}(p^r,N) \to \mathcal {X}(H,N)$
, for
![]() $r\gg 0$
, on which the sheaf
$r\gg 0$
, on which the sheaf
![]() $\mathbb {L}_n$
is constant.
$\mathbb {L}_n$
is constant.
Given a profinite representation L of H, that is, an inverse limit
![]() $L=\displaystyle {\lim _{\infty \leftarrow n}} L_n$
of finite representations
$L=\displaystyle {\lim _{\infty \leftarrow n}} L_n$
of finite representations
![]() $L_n$
for
$L_n$
for
![]() $n\in {\mathbb N}$
, we let
$n\in {\mathbb N}$
, we let
![]() $\mathbb {L}$
be the inverse limit
$\mathbb {L}$
be the inverse limit
![]() $\mathbb {L}=\displaystyle {\lim _{\infty \leftarrow n}} \mathbb {L}_n$
. It is a sheaf on
$\mathbb {L}=\displaystyle {\lim _{\infty \leftarrow n}} \mathbb {L}_n$
. It is a sheaf on
![]() $\mathcal {X}(H,N)_{\mathrm {ket}}$
. Notice that using the scheme
$\mathcal {X}(H,N)_{\mathrm {ket}}$
. Notice that using the scheme
![]() $X(H,N)$
one gets, as mentioned before, a sheaf on
$X(H,N)$
one gets, as mentioned before, a sheaf on
![]() $X(H,N)_{\mathrm {ket}}$
, that we will denote
$X(H,N)_{\mathrm {ket}}$
, that we will denote
![]() $\mathbb {L}$
. We have the following GAGA type of results:
$\mathbb {L}$
. We have the following GAGA type of results:
Theorem 4.10. For every
![]() $i\in {\mathbb N}$
, the maps
$i\in {\mathbb N}$
, the maps
are isomorphisms. Analogously, the natural map
is an almost isomorphism.
Proof. The result for each
![]() $\mathbb {L}_n$
follows from the discussion in §2.4 and from Proposition 2.1.
$\mathbb {L}_n$
follows from the discussion in §2.4 and from Proposition 2.1.
Consider the natural map
![]() $\displaystyle {\lim _{\leftarrow }}\colon \mathrm {Sh}^{\mathbb N}(Z) \to \mathrm {Sh}(Z)$
from inverse systems of sheaves on
$\displaystyle {\lim _{\leftarrow }}\colon \mathrm {Sh}^{\mathbb N}(Z) \to \mathrm {Sh}(Z)$
from inverse systems of sheaves on
![]() $Z=X(H,N)_{\mathrm {pke}}$
, and
$Z=X(H,N)_{\mathrm {pke}}$
, and
![]() $Z=\mathcal {X}(H,N)_{\mathrm {pke}}$
, respectively. Using the existence of bases of log affinoid perfectoid opens with the properties recalled in §2.3, it follows from [Reference Scholze22, lemma 3.18] that we have
$Z=\mathcal {X}(H,N)_{\mathrm {pke}}$
, respectively. Using the existence of bases of log affinoid perfectoid opens with the properties recalled in §2.3, it follows from [Reference Scholze22, lemma 3.18] that we have
![]() $\mathrm {R}^i \displaystyle {\lim _{\leftarrow }} (\mathbb {L})=0$
, both in the algebraic and in the adic setting, and
$\mathrm {R}^i \displaystyle {\lim _{\leftarrow }} (\mathbb {L})=0$
, both in the algebraic and in the adic setting, and
![]() $\mathrm {R}^i \displaystyle {\lim _{\leftarrow }} \bigl ( \mathbb {L}\widehat {\otimes } \widehat {{\cal O}}_{\mathcal {X}(H,N)}^+\bigr )=0$
for
$\mathrm {R}^i \displaystyle {\lim _{\leftarrow }} \bigl ( \mathbb {L}\widehat {\otimes } \widehat {{\cal O}}_{\mathcal {X}(H,N)}^+\bigr )=0$
for
![]() $i\geq 1$
. Hence,
$i\geq 1$
. Hence,
![]() $\mathrm {H}^j\bigl (Z,\mathbb {L}\bigr )$
and
$\mathrm {H}^j\bigl (Z,\mathbb {L}\bigr )$
and
![]() $\mathrm {H}^j\bigl (\mathcal {X}(H,N)_{\mathrm {pke}},\mathbb {L}\widehat {\otimes } \widehat {{\cal O}}_{\mathcal {X}(H,N)}^+\bigr )$
coincide with the derived functors
$\mathrm {H}^j\bigl (\mathcal {X}(H,N)_{\mathrm {pke}},\mathbb {L}\widehat {\otimes } \widehat {{\cal O}}_{\mathcal {X}(H,N)}^+\bigr )$
coincide with the derived functors
![]() $\mathrm {H}^j\bigl (Z,(\mathbb {L}_n)_{n\in {\mathbb N}}\bigr )$
, resp.
$\mathrm {H}^j\bigl (Z,(\mathbb {L}_n)_{n\in {\mathbb N}}\bigr )$
, resp.
![]() $ \mathrm {H}^j\bigl (\mathcal {X}(H,N)_{\mathrm {pke}}, (\mathbb {L}_n \otimes {\cal O}_{\mathcal {X}(H,N)_{\mathrm {pke}}}^+)_{n\in {\mathbb N}}\bigr ) $
of
$ \mathrm {H}^j\bigl (\mathcal {X}(H,N)_{\mathrm {pke}}, (\mathbb {L}_n \otimes {\cal O}_{\mathcal {X}(H,N)_{\mathrm {pke}}}^+)_{n\in {\mathbb N}}\bigr ) $
of
![]() $\displaystyle {\lim _{\leftarrow }} \mathrm {H}^0(Z,\_) $
introduced by [Reference Jannsen19] on the inverse system
$\displaystyle {\lim _{\leftarrow }} \mathrm {H}^0(Z,\_) $
introduced by [Reference Jannsen19] on the inverse system
![]() $\mathrm {Sh}^{\mathbb N}(Z)$
. Due to [Reference Jannsen19, Prop. 1.6], these cohomology groups sit in exact sequences
$\mathrm {Sh}^{\mathbb N}(Z)$
. Due to [Reference Jannsen19, Prop. 1.6], these cohomology groups sit in exact sequences
and similarly for the inverse system
![]() $(\mathbb {L}_n \otimes {\cal O}_{\mathcal {X}(H,N)_{\mathrm {pke}}}^+)_{n\in {\mathbb N}}$
. The maps in the theorem are compatible with these sequences, and the claims follow from the finite case, that is, for the sheaves
$(\mathbb {L}_n \otimes {\cal O}_{\mathcal {X}(H,N)_{\mathrm {pke}}}^+)_{n\in {\mathbb N}}$
. The maps in the theorem are compatible with these sequences, and the claims follow from the finite case, that is, for the sheaves
![]() $\mathbb {L}_n$
.
$\mathbb {L}_n$
.
Remark 4.11. The sheaf
![]() $\mathbb {L}$
has the property that its pullback to the perfectoid space
$\mathbb {L}$
has the property that its pullback to the perfectoid space
![]() $\mathcal {X}(p^{\infty },N)$
is constant and coincides, together with the its H-action, with
$\mathcal {X}(p^{\infty },N)$
is constant and coincides, together with the its H-action, with
![]() $\pi _{\mathrm {HT}}^{-1}\big (L)$
where we view L as a constant, H-equivariant sheaf on
$\pi _{\mathrm {HT}}^{-1}\big (L)$
where we view L as a constant, H-equivariant sheaf on
![]() $\mathbb {P}^1$
(compare with [Reference Caraiani and Scholze10, §2.3] for the case of p-adic automorphic étale sheaves).
$\mathbb {P}^1$
(compare with [Reference Caraiani and Scholze10, §2.3] for the case of p-adic automorphic étale sheaves).
Example 4.12. Consider on
![]() $\mathcal {X}(p^{\infty },N) $
trivializations
$\mathcal {X}(p^{\infty },N) $
trivializations
![]() $T_p E = {\mathbb Z}_p a \oplus {\mathbb Z}_p b$
. The group
$T_p E = {\mathbb Z}_p a \oplus {\mathbb Z}_p b$
. The group
![]() $\mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
acts on the left on the family of trivializations: Given such a basis
$\mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
acts on the left on the family of trivializations: Given such a basis
![]() $\mathcal {A}:=\{a,b\}$
as above and a matrix
$\mathcal {A}:=\{a,b\}$
as above and a matrix
![]() $M\in \mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
, we get a new basis
$M\in \mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
, we get a new basis
![]() $\mathcal {A}':=(a',b'):=(a ,b) M$
. If we think of a trivialization as an isomorphism
$\mathcal {A}':=(a',b'):=(a ,b) M$
. If we think of a trivialization as an isomorphism
![]() $\psi _{\mathcal {A}}\colon T_p E\cong {\mathbb Z}_p^2$
, then
$\psi _{\mathcal {A}}\colon T_p E\cong {\mathbb Z}_p^2$
, then
![]() $\psi _{\mathcal {A}'}$
is
$\psi _{\mathcal {A}'}$
is
![]() $\psi _{\mathcal {A}}$
times left multiplication by M. Thus,
$\psi _{\mathcal {A}}$
times left multiplication by M. Thus,
![]() $T_p(E)$
corresponds to the standard representation
$T_p(E)$
corresponds to the standard representation
![]() $T={\mathbb Z}_p\oplus {\mathbb Z}_p$
of
$T={\mathbb Z}_p\oplus {\mathbb Z}_p$
of
![]() $\mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
.
$\mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
.
This action of M induces a map on dual basis
![]() ${^t}(a^{\vee },b^{\vee })= M{^t}(a^{',\vee },b^{',\vee })$
. Then the trivializations
${^t}(a^{\vee },b^{\vee })= M{^t}(a^{',\vee },b^{',\vee })$
. Then the trivializations
![]() $\psi _{\mathcal {A}^{\vee }}\colon T_p E^{\vee }\cong {\mathbb Z}_p^2$
and
$\psi _{\mathcal {A}^{\vee }}\colon T_p E^{\vee }\cong {\mathbb Z}_p^2$
and
![]() $\psi _{\mathcal {A}^{',\vee }}\colon T_p E^{\vee }\cong {\mathbb Z}_p^2$
induced by the dual bases are such that
$\psi _{\mathcal {A}^{',\vee }}\colon T_p E^{\vee }\cong {\mathbb Z}_p^2$
induced by the dual bases are such that
![]() $ \psi _{\mathcal {A}^{\vee }}$
is
$ \psi _{\mathcal {A}^{\vee }}$
is
![]() $\psi _{\mathcal {A}^{',\vee }}$
times the right multiplication by M. To make the map
$\psi _{\mathcal {A}^{',\vee }}$
times the right multiplication by M. To make the map
![]() $\pi _{\mathrm {HT}}$
equivariant for the
$\pi _{\mathrm {HT}}$
equivariant for the
![]() $\mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
-action we take on
$\mathrm {\mathbf {GL}}_2({\mathbb Z}_p)$
-action we take on
![]() ${\mathbb P}^1_{{\mathbb Q}_p}$
the standard action. If
${\mathbb P}^1_{{\mathbb Q}_p}$
the standard action. If
![]() $\pi _{\mathrm {HT}} (\psi _{\mathcal {A}^{\vee }})=[\alpha ;\beta ]$
and
$\pi _{\mathrm {HT}} (\psi _{\mathcal {A}^{\vee }})=[\alpha ;\beta ]$
and
![]() $\pi _{\mathrm {HT}} (\psi _{\mathcal {A}^{',\vee }})=[\alpha ' ;\beta ']$
, then
$\pi _{\mathrm {HT}} (\psi _{\mathcal {A}^{',\vee }})=[\alpha ' ;\beta ']$
, then
![]() ${^t}[\alpha ;\beta ]=M \, {^t}[\alpha ';\beta ']$
(where
${^t}[\alpha ;\beta ]=M \, {^t}[\alpha ';\beta ']$
(where
![]() ${^t}[\alpha ;\beta ]$
means
${^t}[\alpha ;\beta ]$
means
![]() $[\alpha ;\beta ]$
viewed as column vector).
$[\alpha ;\beta ]$
viewed as column vector).
Consider an s-analytic character
![]() $k\colon {\mathbb Z}_p^{\times }\longrightarrow B^{\ast }$
as in Definition 3.6. Consider the
$k\colon {\mathbb Z}_p^{\times }\longrightarrow B^{\ast }$
as in Definition 3.6. Consider the
![]() ${\mathbb Q}_p$
-module
${\mathbb Q}_p$
-module
![]() $D_k(T_0^{\vee })[n]$
, for
$D_k(T_0^{\vee })[n]$
, for
![]() $n\geq s$
, with action of the Iwahori subroup
$n\geq s$
, with action of the Iwahori subroup
![]() $\mathrm {Iw}_1$
, defined in §3.7. As
$\mathrm {Iw}_1$
, defined in §3.7. As
![]() $D_k(T_0^{\vee })[n]=\bigl (D_k^o(T_0^{\vee })[n]\bigr )[1/p]$
and
$D_k(T_0^{\vee })[n]=\bigl (D_k^o(T_0^{\vee })[n]\bigr )[1/p]$
and
![]() $D_k^o(T_0^{\vee })[n]$
admits a
$D_k^o(T_0^{\vee })[n]$
admits a
![]() $\mathrm {Iw}_1$
-equivariant filtration with finite graded pieces, we get an associated sheaf
$\mathrm {Iw}_1$
-equivariant filtration with finite graded pieces, we get an associated sheaf
![]() ${\mathbb D}_k(T_0^{\vee })[n]$
on the pro-Kummer étale site of
${\mathbb D}_k(T_0^{\vee })[n]$
on the pro-Kummer étale site of
![]() $\mathcal {X}_0(p,N)$
. Then:
$\mathcal {X}_0(p,N)$
. Then:
Proposition 4.13. For every
![]() $i\in {\mathbb N}$
, we have isomorphisms
$i\in {\mathbb N}$
, we have isomorphisms
Proof. The first group is identified with
![]() $\mathrm {H}^i\bigl (X_0(p,N)_{\mathrm {pke}},{\mathbb D}_k(T_0^{\vee })[n] \bigr )\widehat {\otimes } {\mathbb C}_p$
arguing as in [Reference Andreatta, Iovita and Stevens5, Thm. 3.15] using the filtration
$\mathrm {H}^i\bigl (X_0(p,N)_{\mathrm {pke}},{\mathbb D}_k(T_0^{\vee })[n] \bigr )\widehat {\otimes } {\mathbb C}_p$
arguing as in [Reference Andreatta, Iovita and Stevens5, Thm. 3.15] using the filtration
![]() $\mathrm {Fil}^{\bullet } {\mathbb D}_k(T_0^{\vee })[n]$
discussed in §3.5. As
$\mathrm {Fil}^{\bullet } {\mathbb D}_k(T_0^{\vee })[n]$
discussed in §3.5. As
![]() $\widehat {{\cal O}}_{\mathcal {X}_0(p,N)}=\widehat {{\cal O}}_{\mathcal {X}_0(p,N)}^+[1/p]$
and cohomology commutes with direct limits, the conclusion follows from Theorem 4.10 and inverting p.
$\widehat {{\cal O}}_{\mathcal {X}_0(p,N)}=\widehat {{\cal O}}_{\mathcal {X}_0(p,N)}^+[1/p]$
and cohomology commutes with direct limits, the conclusion follows from Theorem 4.10 and inverting p.
For every
![]() $s\geq 1$
, we have actions of Hecke operators on
$s\geq 1$
, we have actions of Hecke operators on
![]() $\mathrm {H}^i\bigl (\mathcal {X}_0(p^s,N)_{\mathrm {pke}},{\mathbb D}_k(T_0^{\vee })[n]\widehat {\otimes } \widehat {{\cal O}}_{\mathcal {X}_0(p^s,N)}\bigr )$
as follows. Let
$\mathrm {H}^i\bigl (\mathcal {X}_0(p^s,N)_{\mathrm {pke}},{\mathbb D}_k(T_0^{\vee })[n]\widehat {\otimes } \widehat {{\cal O}}_{\mathcal {X}_0(p^s,N)}\bigr )$
as follows. Let
![]() $\ell $
be a prime integer not dividing N, and let
$\ell $
be a prime integer not dividing N, and let
![]() $q_1,q_2\colon X_0(p,N,\ell )\to X_0(p,N)$
be as in §4.5. For
$q_1,q_2\colon X_0(p,N,\ell )\to X_0(p,N)$
be as in §4.5. For
![]() $\ell \neq p$
, we have natural isomorphisms
$\ell \neq p$
, we have natural isomorphisms
![]() $q_1^{\ast }\bigl ({\mathbb D}_k^o(T_0^{\vee })[n]\bigr ) \to q_2^{\ast }\bigl ({\mathbb D}_k^o(T_0^{\vee })[n]\bigr )$
inducing a map
$q_1^{\ast }\bigl ({\mathbb D}_k^o(T_0^{\vee })[n]\bigr ) \to q_2^{\ast }\bigl ({\mathbb D}_k^o(T_0^{\vee })[n]\bigr )$
inducing a map
Inverting p, taking
![]() $q_{2,\ast }$
and using the trace map
$q_{2,\ast }$
and using the trace map
![]() $\mathrm {Tr}\colon q_{2,\ast } q_2^{\ast } \to \mathrm {Id}$
of Lemma 4.7, we get a map
$\mathrm {Tr}\colon q_{2,\ast } q_2^{\ast } \to \mathrm {Id}$
of Lemma 4.7, we get a map
For
![]() $\ell =p$
, it follows by taking the dual of the
$\ell =p$
, it follows by taking the dual of the
![]() $\mathrm {Iw}_s$
-equivariant map
$\mathrm {Iw}_s$
-equivariant map
![]() $\pi _n$
of §3.5.2 that we have a map
$\pi _n$
of §3.5.2 that we have a map
![]() $\mathcal {U}_p\colon q_1^{\ast }\bigl ({\mathbb D}_k^o(T_0^{\vee })[n]\bigr ) \to q_2^{\ast }\bigl ({\mathbb D}_k^o(T_0^{\vee })[n+1]\bigr )$
and, hence, a map
$\mathcal {U}_p\colon q_1^{\ast }\bigl ({\mathbb D}_k^o(T_0^{\vee })[n]\bigr ) \to q_2^{\ast }\bigl ({\mathbb D}_k^o(T_0^{\vee })[n+1]\bigr )$
and, hence, a map
Inverting p, taking
![]() $q_{2,\ast }$
and using the trace map
$q_{2,\ast }$
and using the trace map
![]() $\mathrm {Tr}\colon q_{2,\ast } q_2^{\ast } \to \mathrm {Id}$
, we get a map
$\mathrm {Tr}\colon q_{2,\ast } q_2^{\ast } \to \mathrm {Id}$
, we get a map
We have a restriction map
![]() $D_k(T_0^{\vee })[n+1]\to D_k(T_0^{\vee })[n] $
which is
$D_k(T_0^{\vee })[n+1]\to D_k(T_0^{\vee })[n] $
which is
![]() $\mathrm {Iw}_s$
-equivariant and defines a map
$\mathrm {Iw}_s$
-equivariant and defines a map
![]() ${\mathbb D}_k(T_0^{\vee })[n+1] \to {\mathbb D}_k(T_0^{\vee })[n] $
. We finally get a morphism
${\mathbb D}_k(T_0^{\vee })[n+1] \to {\mathbb D}_k(T_0^{\vee })[n] $
. We finally get a morphism
Taking cohomology groups over
![]() $\mathcal {X}_0(p^s,N)_{\mathrm {pke}}$
and using the map
$\mathcal {X}_0(p^s,N)_{\mathrm {pke}}$
and using the map
we get Hecke operators
 $$ \begin{align} T_{\ell}, U_p^{\mathrm{naive}}&\colon \mathrm{H}^i\bigl(\mathcal{X}_0(p^s,N)_{\mathrm{pke}},{\mathbb D}_k(T_0^{\vee})[n]\widehat{\otimes} \widehat{{\cal O}}_{\mathcal{X}_0(p^s,N)}\bigr)\nonumber\\ &\quad \to \mathrm{H}^i\bigl(\mathcal{X}_0(p^s,N)_{\mathrm{pke}},{\mathbb D}_k(T_0^{\vee})[n]\widehat{\otimes} \widehat{{\cal O}}_{\mathcal{X}_0(p^s,N)}\bigr). \end{align} $$
$$ \begin{align} T_{\ell}, U_p^{\mathrm{naive}}&\colon \mathrm{H}^i\bigl(\mathcal{X}_0(p^s,N)_{\mathrm{pke}},{\mathbb D}_k(T_0^{\vee})[n]\widehat{\otimes} \widehat{{\cal O}}_{\mathcal{X}_0(p^s,N)}\bigr)\nonumber\\ &\quad \to \mathrm{H}^i\bigl(\mathcal{X}_0(p^s,N)_{\mathrm{pke}},{\mathbb D}_k(T_0^{\vee})[n]\widehat{\otimes} \widehat{{\cal O}}_{\mathcal{X}_0(p^s,N)}\bigr). \end{align} $$
(Here we introduce the unnormalized operator
![]() $U_p^{\mathrm {naive}}$
which is
$U_p^{\mathrm {naive}}$
which is
![]() $p $
times the standard operator
$p $
times the standard operator
![]() $U_p$
as it preserves integral structures, a fact that will be of crucial importance in section §5.)
$U_p$
as it preserves integral structures, a fact that will be of crucial importance in section §5.)
4.7 A comparison result on
 $\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
$\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
Consider an r-analytic weight
![]() $k\colon {\mathbb Z}_p^{\ast } \to B^{\ast }$
as in Definition 3.6 and integers
$k\colon {\mathbb Z}_p^{\ast } \to B^{\ast }$
as in Definition 3.6 and integers
![]() $ n\geq m$
as in Proposition 4.5, and define the sheaf
$ n\geq m$
as in Proposition 4.5, and define the sheaf
The aim of this section is to prove that for m large enough it admits a decreasing filtration
![]() $\mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n]$
for
$\mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n]$
for
![]() $h\geq -1$
with the following properties.
$h\geq -1$
with the following properties.
Proposition 4.14. The following hold:
-
i. For
 $n\ge m'\geq m$
, we have
$n\ge m'\geq m$
, we have
 $\mathrm {Fil}^{\bullet } \mathfrak {D}_{k,\infty }^{o,(m)}[n] \widehat {\otimes }_{ \widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_{\infty }^{(m)}}^+} \widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_{\infty }^{(m')}}^+\cong \mathrm {Fil}^{\bullet } \mathfrak {D}_{k,\infty }^{o,(m')}[n] $
;
$\mathrm {Fil}^{\bullet } \mathfrak {D}_{k,\infty }^{o,(m)}[n] \widehat {\otimes }_{ \widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_{\infty }^{(m)}}^+} \widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_{\infty }^{(m')}}^+\cong \mathrm {Fil}^{\bullet } \mathfrak {D}_{k,\infty }^{o,(m')}[n] $
; -
ii. We have a surjective map
 $\mathrm {Gr}^{-1} \mathfrak {D}_{k,\infty }^{o,(m)}[n]=\mathfrak {D}_{k,\infty }^{o,(m)}[n]/\mathrm {Fil}^0 \mathfrak {D}_{k,\infty }^{o,(m)}[n]\longrightarrow$
$\mathrm {Gr}^{-1} \mathfrak {D}_{k,\infty }^{o,(m)}[n]=\mathfrak {D}_{k,\infty }^{o,(m)}[n]/\mathrm {Fil}^0 \mathfrak {D}_{k,\infty }^{o,(m)}[n]\longrightarrow$
 $\hspace{2pt}\omega ^{k}_E \otimes _{{\cal O}_{\mathcal {X}_0(p^n, N)_{\infty }^{(m)}}^+} \widehat {{\cal O}}_{\mathcal {X}_0(p^n, N)_{\infty }^{(m)}}^+ $
, where
$\hspace{2pt}\omega ^{k}_E \otimes _{{\cal O}_{\mathcal {X}_0(p^n, N)_{\infty }^{(m)}}^+} \widehat {{\cal O}}_{\mathcal {X}_0(p^n, N)_{\infty }^{(m)}}^+ $
, where
 $\omega _E^k$
is the sheaf defined in §4.4;
$\omega _E^k$
is the sheaf defined in §4.4; -
iii. We have an isomorphism
 $$ \begin{align*} \mathrm{H}^1\bigl(\mathcal{X}_0(p^n, N)_{\infty,{\mathrm{pke}}}^{(m)}, \omega^{k}_E \otimes_{{\cal O}_{\mathcal{X}_0(p^s,N)_{\infty}^{(m)}}^+} \widehat{{\cal O}}_{\mathcal{X}_0(p^n, N)_{\infty}^{(m)}} \bigr)\cong \mathrm{H}^0\bigl(\mathcal{X}_0(p^n, N)_{\infty}^{(m)},\omega^{k+2}_E\bigr)[1/p];\\[-9pt] \end{align*} $$
$$ \begin{align*} \mathrm{H}^1\bigl(\mathcal{X}_0(p^n, N)_{\infty,{\mathrm{pke}}}^{(m)}, \omega^{k}_E \otimes_{{\cal O}_{\mathcal{X}_0(p^s,N)_{\infty}^{(m)}}^+} \widehat{{\cal O}}_{\mathcal{X}_0(p^n, N)_{\infty}^{(m)}} \bigr)\cong \mathrm{H}^0\bigl(\mathcal{X}_0(p^n, N)_{\infty}^{(m)},\omega^{k+2}_E\bigr)[1/p];\\[-9pt] \end{align*} $$
-
iv. The map
induced by the projection onto $$ \begin{align*}&\mathrm{H}^1\bigl(\mathcal{X}_0(p^n, N)_{\infty,{\mathrm{pke}}}^{(m)}, \mathfrak{D}_{k,\infty}^{o,(m)}[n] /\mathrm{Fil}^h \mathfrak{D}_{k,\infty}^{o,(m)}[n] \bigr)\\ &\quad \to \mathrm{H}^1\bigl(\mathcal{X}_0(p^n, N)_{\infty,{\mathrm{pke}}}^{(m)}, \omega^{k}_E \otimes_{{\cal O}_{\mathcal{X}_0(p^s,N)_{\infty}^{(m)}}^+} \widehat{{\cal O}}_{\mathcal{X}_0(p^n, N)_{\infty}^{(m)}}^+\bigr),\\[-9pt] \end{align*} $$
$$ \begin{align*}&\mathrm{H}^1\bigl(\mathcal{X}_0(p^n, N)_{\infty,{\mathrm{pke}}}^{(m)}, \mathfrak{D}_{k,\infty}^{o,(m)}[n] /\mathrm{Fil}^h \mathfrak{D}_{k,\infty}^{o,(m)}[n] \bigr)\\ &\quad \to \mathrm{H}^1\bigl(\mathcal{X}_0(p^n, N)_{\infty,{\mathrm{pke}}}^{(m)}, \omega^{k}_E \otimes_{{\cal O}_{\mathcal{X}_0(p^s,N)_{\infty}^{(m)}}^+} \widehat{{\cal O}}_{\mathcal{X}_0(p^n, N)_{\infty}^{(m)}}^+\bigr),\\[-9pt] \end{align*} $$
 $\mathrm {Gr}^{-1} \mathfrak {D}_{k,\infty }^{o,(m)}[n] $
and (ii), has kernel and cokernel annihilated by a power
$\mathrm {Gr}^{-1} \mathfrak {D}_{k,\infty }^{o,(m)}[n] $
and (ii), has kernel and cokernel annihilated by a power
 $p^{a h}$
of p (with a depending on n);
$p^{a h}$
of p (with a depending on n);
-
v.
 $\mathrm {H}^i\bigl (\mathcal {X}_0(p^n, N)_{\infty ,{\mathrm {pke}}}^{(m)}, \mathfrak {D}_{k,\infty }^{o,(m)}[n] /\mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n] \bigr )$
is equal to
$\mathrm {H}^i\bigl (\mathcal {X}_0(p^n, N)_{\infty ,{\mathrm {pke}}}^{(m)}, \mathfrak {D}_{k,\infty }^{o,(m)}[n] /\mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n] \bigr )$
is equal to
 $\mathrm {H}^0\bigl (\mathcal {X}_0(p^n, N)_{\infty }^{(m)}, \mathrm {Gr}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n] \bigr ) $
for
$\mathrm {H}^0\bigl (\mathcal {X}_0(p^n, N)_{\infty }^{(m)}, \mathrm {Gr}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n] \bigr ) $
for
 $i=0$
, and it is
$i=0$
, and it is
 $0$
for
$0$
for
 $i\geq 2$
.
$i\geq 2$
.
Proof. Recall the surjective map
from equation (2) and Proposition 4.5. It is defined for every m large enough and
![]() $\omega _E^{\mathrm {mod}} $
is an invertible
$\omega _E^{\mathrm {mod}} $
is an invertible
![]() ${\cal O}_{\mathcal {X}_0(p^n,N)_{\infty }^{(m)}}^+$
-module. We also assume that over
${\cal O}_{\mathcal {X}_0(p^n,N)_{\infty }^{(m)}}^+$
-module. We also assume that over
![]() $\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
we have a canonical subgroup
$\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
we have a canonical subgroup
![]() $C_r$
of order
$C_r$
of order
![]() $p^r$
. Consider the natural projection
$p^r$
. Consider the natural projection
![]() $j_n\colon \mathcal {X}(p^n,N)_{\infty }^{(m)} \to \mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
; then
$j_n\colon \mathcal {X}(p^n,N)_{\infty }^{(m)} \to \mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
; then
![]() $j_n$
is Kummer étale and Galois with group
$j_n$
is Kummer étale and Galois with group
![]() $\Delta _n$
the subgroup of
$\Delta _n$
the subgroup of
![]() $\mathrm {\mathbf {GL}}_2({\mathbb Z}/p^n{\mathbb Z})$
of upper triangular matrices. In particular, to define a sheaf on
$\mathrm {\mathbf {GL}}_2({\mathbb Z}/p^n{\mathbb Z})$
of upper triangular matrices. In particular, to define a sheaf on
![]() $\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}$
is equivalent to define a sheaf on
$\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}$
is equivalent to define a sheaf on
![]() $\mathcal {X}(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}$
with an action of
$\mathcal {X}(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}$
with an action of
![]() $\Delta _n$
compatible with the action on
$\Delta _n$
compatible with the action on
![]() $\mathcal {X}(p^n,N)_{\infty }^{(m)}$
. In order to define
$\mathcal {X}(p^n,N)_{\infty }^{(m)}$
. In order to define
![]() $\mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n]$
, we define a
$\mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n]$
, we define a
![]() $\Delta _n$
-equivariant filtration on
$\Delta _n$
-equivariant filtration on
![]() $j_n^{\ast } \bigl ( \mathfrak {D}_{k,\infty }^{o,(m)}[n]\bigr )$
.
$j_n^{\ast } \bigl ( \mathfrak {D}_{k,\infty }^{o,(m)}[n]\bigr )$
.
Over
![]() $ \mathcal {X}(p^n,N)_{\infty }^{(m)}$
, we have a trivialization
$ \mathcal {X}(p^n,N)_{\infty }^{(m)}$
, we have a trivialization
such that
![]() $\mathrm {dlog}(a^{\vee })$
is a basis for
$\mathrm {dlog}(a^{\vee })$
is a basis for
![]() $\omega _E^{\mathrm {mod}}/ p^r \omega _E^{\mathrm {mod}}$
as
$\omega _E^{\mathrm {mod}}/ p^r \omega _E^{\mathrm {mod}}$
as
![]() ${\cal O}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+$
-module. Dualizing, we get an injective map
${\cal O}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+$
-module. Dualizing, we get an injective map
with quotient
![]() $\mathcal {Q}$
isomorphic to
$\mathcal {Q}$
isomorphic to
![]() $\omega _E^{\mathrm {mod}}\otimes _{{\cal O}_{\mathcal {X}_0(p,N)_{\infty }^{(m)}}^+} \widehat {{\cal O}}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+$
and such that modulo
$\omega _E^{\mathrm {mod}}\otimes _{{\cal O}_{\mathcal {X}_0(p,N)_{\infty }^{(m)}}^+} \widehat {{\cal O}}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+$
and such that modulo
![]() $p^r$
the section a generates
$p^r$
the section a generates
![]() $\omega _E^{\mathrm {mod,-1}}/p^n \omega _E^{\mathrm {mod,-1}}$
as
$\omega _E^{\mathrm {mod,-1}}/p^n \omega _E^{\mathrm {mod,-1}}$
as
![]() ${\cal O}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+$
-module. Then
${\cal O}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+$
-module. Then
![]() $(\mathrm { dlog})^{\vee }$
induces, for every
$(\mathrm { dlog})^{\vee }$
induces, for every
![]() $\lambda \in {\mathbb Z}/p^n{\mathbb Z}$
, an affine map
$\lambda \in {\mathbb Z}/p^n{\mathbb Z}$
, an affine map
on the pro-Kummer étale site of
![]() $\mathcal {X}(p^n,N)_{\infty }^{(m)}$
. Here and below, the formalism f VBMS is applied with respect to the ideal
$\mathcal {X}(p^n,N)_{\infty }^{(m)}$
. Here and below, the formalism f VBMS is applied with respect to the ideal
![]() ${\cal I}$
generated by
${\cal I}$
generated by
![]() $p^r$
. Notice that
$p^r$
. Notice that
![]() ${\mathbb V}_0\bigl (T_p(E) , a,b-\lambda a\bigr ) \times _{{\mathbb Z}_p} \mathcal {X}(p^n,N)_{\infty }^{(m)}\cong {\mathbb V}_0\bigl (T_p(E)\otimes _{{\mathbb Z}_p} \widehat {{\cal O}}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+,a,b-\lambda b\bigr )$
is a principal homogeneous space under the formal vector group
${\mathbb V}_0\bigl (T_p(E) , a,b-\lambda a\bigr ) \times _{{\mathbb Z}_p} \mathcal {X}(p^n,N)_{\infty }^{(m)}\cong {\mathbb V}_0\bigl (T_p(E)\otimes _{{\mathbb Z}_p} \widehat {{\cal O}}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+,a,b-\lambda b\bigr )$
is a principal homogeneous space under the formal vector group
![]() ${\mathbb V}'\bigl (\mathcal {Q}\bigr ) \subset {\mathbb V}\bigl (\mathcal {Q}\bigr )$
classifying sections of
${\mathbb V}'\bigl (\mathcal {Q}\bigr ) \subset {\mathbb V}\bigl (\mathcal {Q}\bigr )$
classifying sections of
![]() $\mathcal {Q}^{\vee }$
which are zero modulo
$\mathcal {Q}^{\vee }$
which are zero modulo
![]() $p^r$
. We have the invertible
$p^r$
. We have the invertible
![]() ${\cal O}_{\mathcal {X}_0(p,N)_{\infty }^{(m)}}^+\widehat {\otimes } B$
-module
${\cal O}_{\mathcal {X}_0(p,N)_{\infty }^{(m)}}^+\widehat {\otimes } B$
-module
![]() $\omega ^{-k}_E := {\mathbb W}_k(\omega _E^{\mathrm {mod,-1}}, a\big )$
. Set
$\omega ^{-k}_E := {\mathbb W}_k(\omega _E^{\mathrm {mod,-1}}, a\big )$
. Set
Applying the formalism of VBMS, we get the map of sheaves on the pro-Kummer étale site of
![]() $\mathcal {X}(p^n,N)_{\infty }^{(m)}$
$\mathcal {X}(p^n,N)_{\infty }^{(m)}$
Using that
![]() ${\mathbb V}_0\bigl (T_p(E)\otimes _{{\mathbb Z}_p} \widehat {{\cal O}}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+,a,b +\lambda a\bigr )$
is a principal homogeneous space under
${\mathbb V}_0\bigl (T_p(E)\otimes _{{\mathbb Z}_p} \widehat {{\cal O}}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+,a,b +\lambda a\bigr )$
is a principal homogeneous space under
![]() ${\mathbb V}'\bigl (\mathcal {Q}\bigr )$
, we obtain a
${\mathbb V}'\bigl (\mathcal {Q}\bigr )$
, we obtain a
![]() ${\mathbb V}'\bigl (\mathcal {Q}\bigr )$
-stable increasing filtration
${\mathbb V}'\bigl (\mathcal {Q}\bigr )$
-stable increasing filtration
![]() $\mathrm { Fil}_h \mathfrak {W}_{k,\infty ,\lambda }^{(m)}$
for
$\mathrm { Fil}_h \mathfrak {W}_{k,\infty ,\lambda }^{(m)}$
for
![]() $h\geq 0$
with
$h\geq 0$
with
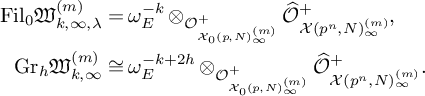 $$ \begin{align} \mathrm{Fil}_0 \mathfrak{W}_{k,\infty,\lambda}^{(m)}&=\omega^{-k}_E \otimes_{{\cal O}_{\mathcal{X}_0(p,N)_{\infty}^{(m)}}^+} \widehat{{\cal O}}_{\mathcal{X}(p^n,N)_{\infty}^{(m)}}^+,\nonumber\\ \mathrm{Gr}_h \mathfrak{W}_{k,\infty}^{(m)}&\cong \omega^{-k+2h}_E \otimes_{{\cal O}_{\mathcal{X}_0(p,N)_{\infty}^{(m)}}^+} \widehat{{\cal O}}_{\mathcal{X}(p^n,N)_{\infty}^{(m)}}^+. \end{align} $$
$$ \begin{align} \mathrm{Fil}_0 \mathfrak{W}_{k,\infty,\lambda}^{(m)}&=\omega^{-k}_E \otimes_{{\cal O}_{\mathcal{X}_0(p,N)_{\infty}^{(m)}}^+} \widehat{{\cal O}}_{\mathcal{X}(p^n,N)_{\infty}^{(m)}}^+,\nonumber\\ \mathrm{Gr}_h \mathfrak{W}_{k,\infty}^{(m)}&\cong \omega^{-k+2h}_E \otimes_{{\cal O}_{\mathcal{X}_0(p,N)_{\infty}^{(m)}}^+} \widehat{{\cal O}}_{\mathcal{X}(p^n,N)_{\infty}^{(m)}}^+. \end{align} $$
See [Reference Andreatta and Iovita2] and [Reference Andreatta, Iovita and Stevens6, Prop. 5.2]. Taking
![]() $\widehat {{\cal O}}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+$
-duals, we get a sheaf and a decreasing filtration
$\widehat {{\cal O}}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+$
-duals, we get a sheaf and a decreasing filtration
on the pro-Kummer étale site of
![]() $\mathcal {X}(p^n,N)_{\infty }^{(m)}$
. Here,
$\mathcal {X}(p^n,N)_{\infty }^{(m)}$
. Here,
![]() $\mathrm {Fil}^h \mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee }$
consists of those sections of
$\mathrm {Fil}^h \mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee }$
consists of those sections of
![]() $\mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee }$
which are zero on
$\mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee }$
which are zero on
![]() $\mathrm {Fil}_h \mathfrak {W}_{k,\infty ,\lambda }^{(m)}$
(where we set
$\mathrm {Fil}_h \mathfrak {W}_{k,\infty ,\lambda }^{(m)}$
(where we set
![]() $\mathrm {Fil}_{-1}\mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee }=0$
so that
$\mathrm {Fil}_{-1}\mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee }=0$
so that
![]() $\mathrm {Fil}^{-1} \mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee })= \mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee }$
). Then
$\mathrm {Fil}^{-1} \mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee })= \mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee }$
). Then
Due to Proposition 3.8, we have a
![]() $\Delta _n$
-equivariant isomorphism
$\Delta _n$
-equivariant isomorphism
and we set
![]() $\mathrm {Fil}^h j_n^{\ast } \bigl ( \mathfrak {D}_{k,\infty }^{o,(m)}[n]\bigr )$
to be the filtration corresponding to
$\mathrm {Fil}^h j_n^{\ast } \bigl ( \mathfrak {D}_{k,\infty }^{o,(m)}[n]\bigr )$
to be the filtration corresponding to
![]() $\oplus _{\lambda \in {\mathbb Z}/p^n{\mathbb Z}} \mathrm {Fil}^h\mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee } $
. The map
$\oplus _{\lambda \in {\mathbb Z}/p^n{\mathbb Z}} \mathrm {Fil}^h\mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee } $
. The map
![]() $\oplus _ \lambda \rho _{\lambda }^k$
defines a map
$\oplus _ \lambda \rho _{\lambda }^k$
defines a map
![]() $\rho ^k\colon \omega ^{-k}_E \otimes _{{\cal O}_{\mathcal {X}_0(p,N)_{\infty }^{(m)}}^+} \widehat {{\cal O}}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+ \longrightarrow \oplus _{\lambda } \mathfrak {W}_{k,\infty ,\lambda }^{(m)} $
and, hence, a map
$\rho ^k\colon \omega ^{-k}_E \otimes _{{\cal O}_{\mathcal {X}_0(p,N)_{\infty }^{(m)}}^+} \widehat {{\cal O}}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+ \longrightarrow \oplus _{\lambda } \mathfrak {W}_{k,\infty ,\lambda }^{(m)} $
and, hence, a map
By construction, (i) and (ii) hold over
![]() $\mathcal {X}(p^n,N)_{\infty }^{(m)}$
, and to prove those claims we need to show that the given filtration and the map
$\mathcal {X}(p^n,N)_{\infty }^{(m)}$
, and to prove those claims we need to show that the given filtration and the map
![]() $\nu $
are
$\nu $
are
![]() $\Delta _n$
-equivariant. Also, given a sheaf
$\Delta _n$
-equivariant. Also, given a sheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\mathcal {X}_0(p,N)_{\infty }^{(m)}$
, we have a spectral sequence
$\mathcal {X}_0(p,N)_{\infty }^{(m)}$
, we have a spectral sequence
Since the cohomology groups
![]() $\mathrm {H}^j\bigl (\Delta _n,\mathcal {G}\bigr )$
are annihilated by the order of
$\mathrm {H}^j\bigl (\Delta _n,\mathcal {G}\bigr )$
are annihilated by the order of
![]() $\Delta _n$
for
$\Delta _n$
for
![]() $j\geq 1$
, to conclude (iv)–(v) it suffices to prove those claims for
$j\geq 1$
, to conclude (iv)–(v) it suffices to prove those claims for
![]() $\mathcal {X}(p^n,N)_{\infty }^{(m)}$
.
$\mathcal {X}(p^n,N)_{\infty }^{(m)}$
.
The rest of the proof is a computation using the log affinoid perfectoid cover by opens U of the adic space
![]() $\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}$
defined by trivializing the full Tate module
$\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}$
defined by trivializing the full Tate module
![]() $\prod _{\ell } T_{\ell }(E)$
. It is Galois over
$\prod _{\ell } T_{\ell }(E)$
. It is Galois over
![]() $\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}$
with group
$\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}$
with group
![]() $G_U$
. Let
$G_U$
. Let
![]() $\widehat {U}:=\mathrm {Spa}(R,R^+)$
be the associated affinoid perfectoid space as in §2.3. Write
$\widehat {U}:=\mathrm {Spa}(R,R^+)$
be the associated affinoid perfectoid space as in §2.3. Write
![]() $T_p(E)^{\vee }(U)\otimes R^+=e_0 R^+\oplus e_1R^+$
with
$T_p(E)^{\vee }(U)\otimes R^+=e_0 R^+\oplus e_1R^+$
with
![]() $e_0$
mapping to a generator of
$e_0$
mapping to a generator of
![]() $\omega _E^{\mathrm {mod}}$
and
$\omega _E^{\mathrm {mod}}$
and
![]() $e_1$
in the kernel of
$e_1$
in the kernel of
![]() $d\log $
generating
$d\log $
generating
![]() $\omega _E^{\mathrm {mod,-1}}$
. Recall from Proposition 3.8 that
$\omega _E^{\mathrm {mod,-1}}$
. Recall from Proposition 3.8 that
![]() $\mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee }(U)$
is the dual of
$\mathfrak {W}_{k,\infty ,\lambda }^{(m),\vee }(U)$
is the dual of
![]() $\mathfrak {W}_{k,\infty ,\lambda }^{(m)}(U)\cong R^+\otimes B\langle \frac {W_{\lambda }}{1+p^r Z} \rangle \cdot k(1+p^r Z)$
with increasing filtration defined by
$\mathfrak {W}_{k,\infty ,\lambda }^{(m)}(U)\cong R^+\otimes B\langle \frac {W_{\lambda }}{1+p^r Z} \rangle \cdot k(1+p^r Z)$
with increasing filtration defined by
![]() $\mathrm {Fil}^h = \oplus _{i=0}^h R^+\otimes B \bigl (\frac {W_{\lambda }}{1+p^r Z}\bigr )^i \cdot k(1+p^r Z) $
.
$\mathrm {Fil}^h = \oplus _{i=0}^h R^+\otimes B \bigl (\frac {W_{\lambda }}{1+p^r Z}\bigr )^i \cdot k(1+p^r Z) $
.
For every
![]() $\sigma \in G_U$
, we then have
$\sigma \in G_U$
, we then have
![]() $\sigma (e_1)=e_1$
and
$\sigma (e_1)=e_1$
and
![]() $\sigma (e_0)=e_0+\xi (\sigma ) e_1$
. Then,
$\sigma (e_0)=e_0+\xi (\sigma ) e_1$
. Then,
![]() $\sigma (W_{\lambda })=W_{\lambda } +\frac {\xi (\sigma )}{p^n} (1+p^r Z) $
and
$\sigma (W_{\lambda })=W_{\lambda } +\frac {\xi (\sigma )}{p^n} (1+p^r Z) $
and
![]() $\sigma (Z)= Z$
. If
$\sigma (Z)= Z$
. If
![]() $\xi (\sigma )=\alpha + p^r \beta $
then
$\xi (\sigma )=\alpha + p^r \beta $
then
![]() $\sigma (W_{\lambda })=W_{\lambda +\alpha } + \beta (1+p^r Z) $
. Thus, the increasing filtration on
$\sigma (W_{\lambda })=W_{\lambda +\alpha } + \beta (1+p^r Z) $
. Thus, the increasing filtration on
![]() $\oplus _{\lambda \in {\mathbb Z}/p^n{\mathbb Z}}\mathfrak {W}_{k,\infty ,\lambda }^{(m)}$
and the diagonal embedding of
$\oplus _{\lambda \in {\mathbb Z}/p^n{\mathbb Z}}\mathfrak {W}_{k,\infty ,\lambda }^{(m)}$
and the diagonal embedding of
![]() $R^+\otimes B\to \oplus _{\lambda \in {\mathbb Z}/p^n{\mathbb Z}}\mathrm {Fil}^0 \mathfrak {W}_{k,\infty ,\lambda }^{(m)}$
are both stable for the action of
$R^+\otimes B\to \oplus _{\lambda \in {\mathbb Z}/p^n{\mathbb Z}}\mathrm {Fil}^0 \mathfrak {W}_{k,\infty ,\lambda }^{(m)}$
are both stable for the action of
![]() $G_U$
. This concludes the proof of (i) and (ii).
$G_U$
. This concludes the proof of (i) and (ii).
We pass to claims (iii)–(v). As
![]() $\omega ^{k+2}_E$
is a locally free
$\omega ^{k+2}_E$
is a locally free
![]() ${\cal O}_{\mathcal {X}_0(p,N)_{\infty }^{(m)}}^+\widehat {\otimes }B$
-module, we are left to show that
${\cal O}_{\mathcal {X}_0(p,N)_{\infty }^{(m)}}^+\widehat {\otimes }B$
-module, we are left to show that
So to prove claim (iii), we are left to show that that the map (3) is an isomorphism. The étale cohomology of the structure sheaf on U is trivial as recalled in §2.3. Thanks to equation (6), the sheaves
![]() $ \mathfrak {D}_{k,\infty }^{o,(m)}[n] /\mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n] \vert _U$
are extensions of the structure sheaf
$ \mathfrak {D}_{k,\infty }^{o,(m)}[n] /\mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n] \vert _U$
are extensions of the structure sheaf
![]() $\widehat {{\cal O}}_U^+$
so that also their cohomology over U is trivial. Then the cohomology groups in equation (3) and those of
$\widehat {{\cal O}}_U^+$
so that also their cohomology over U is trivial. Then the cohomology groups in equation (3) and those of
![]() $ \mathfrak {D}_{k,\infty }^{o,(m)}[n] /\mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n]$
appearing in (iv) and (v) coincide with the continuous cohomology of
$ \mathfrak {D}_{k,\infty }^{o,(m)}[n] /\mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n]$
appearing in (iv) and (v) coincide with the continuous cohomology of
![]() $G_U$
of the sections of the relevant sheaves over U. This reduces the proof of claims (iii), (iv) and (v) to a Galois cohomology computation for which we refer to [Reference Andreatta, Iovita and Stevens6, Thm. 5.4].
$G_U$
of the sections of the relevant sheaves over U. This reduces the proof of claims (iii), (iv) and (v) to a Galois cohomology computation for which we refer to [Reference Andreatta, Iovita and Stevens6, Thm. 5.4].
We have Hecke operators acting on the cohomology of
![]() $\mathfrak {D}_{k,\infty }^{o,(m)}[n] $
; see equation (4). We assume the hypothesis in the proof of Proposition 4.14.
$\mathfrak {D}_{k,\infty }^{o,(m)}[n] $
; see equation (4). We assume the hypothesis in the proof of Proposition 4.14.
Proposition 4.15. The operator
![]() $U_p^{\mathrm {naive}}=p U_p$
is defined on
$U_p^{\mathrm {naive}}=p U_p$
is defined on
![]() $\mathrm {H}^i\bigl (\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}, \mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n] \bigr )$
for every
$\mathrm {H}^i\bigl (\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}, \mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n] \bigr )$
for every
![]() $h\geq -1$
. There exists an operator
$h\geq -1$
. There exists an operator
![]() $U_{p,h}$
$U_{p,h}$
such that on
![]() $\mathrm {H}^i\bigl (\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}, \mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n] \bigr )$
we have
$\mathrm {H}^i\bigl (\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(m)}, \mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)}[n] \bigr )$
we have
![]() $U_p^{\mathrm {naive}}=p^{h+1} U_{p,h}$
for
$U_p^{\mathrm {naive}}=p^{h+1} U_{p,h}$
for
![]() $i=0$
,
$i=0$
,
![]() $1$
.
$1$
.
Moreover, for every positive integer h the cohomology group
![]() $\mathrm {H}^1\bigl (\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(n)}, \mathfrak {D}_{k,\infty }^{o,(m)}[n] \bigr )[1/p] $
admits a slope
$\mathrm {H}^1\bigl (\mathcal {X}_0(p^n,N)_{\infty ,{\mathrm {pke}}}^{(n)}, \mathfrak {D}_{k,\infty }^{o,(m)}[n] \bigr )[1/p] $
admits a slope
![]() $\leq h$
-decomposition with respect to the
$\leq h$
-decomposition with respect to the
![]() $U_p$
-operator and we have an isomorphism of Hecke modules:
$U_p$
-operator and we have an isomorphism of Hecke modules:
where the tensor product is over the finite extension of
![]() ${\mathbb Q}_p$
over which
${\mathbb Q}_p$
over which
![]() $\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
is defined.
$\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
is defined.
Proof. Recall the construction of the
![]() $U_p$
-operator in equation (4); all steps are defined integrally on
$U_p$
-operator in equation (4); all steps are defined integrally on
![]() $\mathfrak {D}_{k,\infty }^{o,(m)} [n]$
except for the trace
$\mathfrak {D}_{k,\infty }^{o,(m)} [n]$
except for the trace
![]() $\mathrm {Tr}\colon q_{2,\ast } q_2^{\ast }\sim \mathrm {Id}$
, and all steps are defined for
$\mathrm {Tr}\colon q_{2,\ast } q_2^{\ast }\sim \mathrm {Id}$
, and all steps are defined for
![]() $\mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)} [n]$
except possibly for
$\mathrm {Fil}^h \mathfrak {D}_{k,\infty }^{o,(m)} [n]$
except possibly for
We claim that
![]() $\mathcal {U}$
restricts to a map on
$\mathcal {U}$
restricts to a map on
![]() $q_1^{\ast }\bigl (\mathrm {Fil}^h {\mathbb D}_k^o(T_0^{\vee })[n]\widehat {\otimes } \widehat {{\cal O}}_{\mathcal {X}_0(p,N)}^+\bigr ) \to q_2^{\ast }\bigl (\mathrm {Fil}^h {\mathbb D}_k^o(T_0^{\vee })[n+1]\widehat {\otimes } \widehat {{\cal O}}_{\mathcal {X}_0(p,N,p)}^+\bigr )$
which can be written as
$q_1^{\ast }\bigl (\mathrm {Fil}^h {\mathbb D}_k^o(T_0^{\vee })[n]\widehat {\otimes } \widehat {{\cal O}}_{\mathcal {X}_0(p,N)}^+\bigr ) \to q_2^{\ast }\bigl (\mathrm {Fil}^h {\mathbb D}_k^o(T_0^{\vee })[n+1]\widehat {\otimes } \widehat {{\cal O}}_{\mathcal {X}_0(p,N,p)}^+\bigr )$
which can be written as
![]() $p^{h+1}$
times an operator
$p^{h+1}$
times an operator
![]() $\mathcal {U}'$
. Both statements can be checked upon passing to sections over a log affinoid perfectoid. These statements are then proven in [Reference Andreatta, Iovita and Stevens6, Thm. 5.5].
$\mathcal {U}'$
. Both statements can be checked upon passing to sections over a log affinoid perfectoid. These statements are then proven in [Reference Andreatta, Iovita and Stevens6, Thm. 5.5].
The statement on the existence of slope decomposition and the displayed isomorphism are proven as in [Reference Andreatta, Iovita and Stevens6, Thm. 5.1] using Proposition 4.14.
4.8 A comparison result on
 $\mathcal {X}_0(p^n,N)_0^{(m)}$
$\mathcal {X}_0(p^n,N)_0^{(m)}$
As in the previous section, we fix an r-analytic weight
![]() $k\colon {\mathbb Z}_p^{\ast } \to B^{\ast }$
, as in definition 3.6, and we write
$k\colon {\mathbb Z}_p^{\ast } \to B^{\ast }$
, as in definition 3.6, and we write
![]() $u_k\in B[1/p]$
for the element such that
$u_k\in B[1/p]$
for the element such that
![]() $k(a)=\exp u_k \log a$
for
$k(a)=\exp u_k \log a$
for
![]() $a\in 1+p^r {\mathbb Z}_p$
. Note that
$a\in 1+p^r {\mathbb Z}_p$
. Note that
![]() $p^{r} u_k\in B$
. Fix an integer
$p^{r} u_k\in B$
. Fix an integer
![]() $n\geq r$
, and define the sheaf
$n\geq r$
, and define the sheaf
![]() $\mathfrak {D}_{k,0}^{o,(m)}[n]:={\mathbb D}_k^o(T_0^{\vee })[n]\vert _{\mathcal {X}_0(p^n,N)_0^{(m)}} \widehat {\otimes } \widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_0^{(m)}}^+$
. In this case, we have the following.
$\mathfrak {D}_{k,0}^{o,(m)}[n]:={\mathbb D}_k^o(T_0^{\vee })[n]\vert _{\mathcal {X}_0(p^n,N)_0^{(m)}} \widehat {\otimes } \widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_0^{(m)}}^+$
. In this case, we have the following.
Proposition 4.16. For m large enough, there exists an increasing filtration
![]() $\bigl (\mathrm {Fil}_s \mathfrak {D}_{k,0}^{o,(m)}[n]\bigr )_{s\ge 0}$
with the following properties:
$\bigl (\mathrm {Fil}_s \mathfrak {D}_{k,0}^{o,(m)}[n]\bigr )_{s\ge 0}$
with the following properties:
-
i. For
 $m'\geq m$
, we have
$m'\geq m$
, we have
 $\mathrm {Fil}_{\bullet } \mathfrak {D}_{k,0}^{o,(m)}[n] \widehat {\otimes }_{ \widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_0^{(m)}}^+} \widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_0^{(m')}}^+\cong \mathrm {Fil}_{\bullet } \mathfrak {D}_{k,0}^{o,(m')}[n] $
;
$\mathrm {Fil}_{\bullet } \mathfrak {D}_{k,0}^{o,(m)}[n] \widehat {\otimes }_{ \widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_0^{(m)}}^+} \widehat {{\cal O}}_{\mathcal {X}_0(p^n,N)_0^{(m')}}^+\cong \mathrm {Fil}_{\bullet } \mathfrak {D}_{k,0}^{o,(m')}[n] $
; -
ii. For every
 $s\ge 0$
the image of the map is annihilated by the product
$s\ge 0$
the image of the map is annihilated by the product $$ \begin{align*}\mathrm{H}^1\bigl(\mathcal{X}_0(p^n,N)_{0,{\mathrm{pke}}}^{(m)},\mathrm{ Fil}_s \mathfrak{D}_{k,\infty}^{o,(m)}[n] \bigr) \to \mathrm{H}^1\bigl(\mathcal{X}_0(p^n,N)_{0,{\mathrm{pke}}}^{(m)}, \mathfrak{D}_{k,\infty}^{o,(m)}[n] \bigr)\end{align*} $$
$$ \begin{align*}\mathrm{H}^1\bigl(\mathcal{X}_0(p^n,N)_{0,{\mathrm{pke}}}^{(m)},\mathrm{ Fil}_s \mathfrak{D}_{k,\infty}^{o,(m)}[n] \bigr) \to \mathrm{H}^1\bigl(\mathcal{X}_0(p^n,N)_{0,{\mathrm{pke}}}^{(m)}, \mathfrak{D}_{k,\infty}^{o,(m)}[n] \bigr)\end{align*} $$
 $p^{(r+c) s} \left (\begin {matrix} u_k \cr s \end {matrix} \right ) $
(with c depending on n).
$p^{(r+c) s} \left (\begin {matrix} u_k \cr s \end {matrix} \right ) $
(with c depending on n).
Proof. We follow closely the proof of Proposition 4.14. We take m large enough so that E admits a canoncial subgroup
![]() $C_n$
of level
$C_n$
of level
![]() $p^n$
over
$p^n$
over
![]() $\mathcal {X}_0(p^n,N)_{0}^{(m)}$
. Note that the canonical subgroup
$\mathcal {X}_0(p^n,N)_{0}^{(m)}$
. Note that the canonical subgroup
![]() $C_n$
and the level subgroup
$C_n$
and the level subgroup
![]() $H_n$
are distinct.
$H_n$
are distinct.
The natural projection
![]() $j_n\colon \mathcal {X}(p^n,N)_0^{(m)} \to \mathcal {X}_0(p^n,N)_0^{(m)}$
is Kummer étale with automorphism group
$j_n\colon \mathcal {X}(p^n,N)_0^{(m)} \to \mathcal {X}_0(p^n,N)_0^{(m)}$
is Kummer étale with automorphism group
![]() $\Delta _n$
isomorphic to the subgroup of
$\Delta _n$
isomorphic to the subgroup of
![]() $\mathrm {\mathbf {GL}}_2({\mathbb Z}/p^n{\mathbb Z})$
of matrices that are upper triangular modulo
$\mathrm {\mathbf {GL}}_2({\mathbb Z}/p^n{\mathbb Z})$
of matrices that are upper triangular modulo
![]() $p^n$
. It is not a Galois cover as
$p^n$
. It is not a Galois cover as
![]() $ \mathcal {X}(p^n,N)_0^{(m)} $
is not connected. In fact, we have a trivialization
$ \mathcal {X}(p^n,N)_0^{(m)} $
is not connected. In fact, we have a trivialization
![]() $T_p E/p^n T_p E=({\mathbb Z}/p^n{\mathbb Z}) a \oplus ({\mathbb Z}/p^n{\mathbb Z}) b$
over
$T_p E/p^n T_p E=({\mathbb Z}/p^n{\mathbb Z}) a \oplus ({\mathbb Z}/p^n{\mathbb Z}) b$
over
![]() $\mathcal {X}(p^n,N)_0^{(m)}$
. As recalled in 4.2, we have a decomposition
$\mathcal {X}(p^n,N)_0^{(m)}$
. As recalled in 4.2, we have a decomposition
![]() $\mathcal {X}(p^n,N)_{0}^{(m)}=\amalg _{\xi \in {\mathbb Z}/p^n {\mathbb Z}} \mathcal {X}(p^n,N)_{0,\xi }^{(m)}$
where over
$\mathcal {X}(p^n,N)_{0}^{(m)}=\amalg _{\xi \in {\mathbb Z}/p^n {\mathbb Z}} \mathcal {X}(p^n,N)_{0,\xi }^{(m)}$
where over
![]() $\mathcal {X}(p^n,N)_{0,\xi }^{(m)}$
we have
$\mathcal {X}(p^n,N)_{0,\xi }^{(m)}$
we have
![]() $\mathrm {dlog}(a^{\vee })=\xi \mathrm {dlog} (b^{\vee })$
modulo
$\mathrm {dlog}(a^{\vee })=\xi \mathrm {dlog} (b^{\vee })$
modulo
![]() $p^n$
. We recall that to give a sheaf on
$p^n$
. We recall that to give a sheaf on
![]() $\mathcal {X}_0(p,N)_{0,{\mathrm {pke}}}^{(m)}$
is equivalent to give a sheaf on
$\mathcal {X}_0(p,N)_{0,{\mathrm {pke}}}^{(m)}$
is equivalent to give a sheaf on
![]() $\mathcal {X}(p^n,N)_{0,{\mathrm {pke}}}^{(m)}$
endowed with a compatible action of
$\mathcal {X}(p^n,N)_{0,{\mathrm {pke}}}^{(m)}$
endowed with a compatible action of
![]() $\Delta _n$
. In particular to define
$\Delta _n$
. In particular to define
![]() $\mathrm {Fil}_s \mathfrak {D}_{k,\infty }^{o,(m)}[n] $
, we define the filtration over
$\mathrm {Fil}_s \mathfrak {D}_{k,\infty }^{o,(m)}[n] $
, we define the filtration over
![]() $\mathcal {X}(p^n,N)_{0,{\mathrm {pke}}}^{(m)}$
and we prove that it is stable for the action of
$\mathcal {X}(p^n,N)_{0,{\mathrm {pke}}}^{(m)}$
and we prove that it is stable for the action of
![]() $\Delta _n$
. The maps
$\Delta _n$
. The maps
![]() $\mathrm {dlog}$
and
$\mathrm {dlog}$
and
![]() $\mathrm {dlog}^{\vee }$
define an exact sequence of sheaves on the pro-Kummer étale site of
$\mathrm {dlog}^{\vee }$
define an exact sequence of sheaves on the pro-Kummer étale site of
![]() $\mathcal {X}(p^n,N)_0^{(m)}$
:
$\mathcal {X}(p^n,N)_0^{(m)}$
:
 $$ \begin{align*} Q&:=\omega_E^{\mathrm{mod,-1}} \otimes_{{\cal O}_{\mathcal{X}_0(p^n,N)_0^{(m)}}^+} \widehat{{\cal O}}_{\mathcal{X}(p^n,N)_0^{(m)}}^+ \longrightarrow T_p(E) \otimes_{{\mathbb Z}_p} \widehat{{\cal O}}_{\mathcal{X}(p^n,N)_0^{(m)}}^+\\ &\quad \longrightarrow \omega_E^{\mathrm{mod}}\otimes_{{\cal O}_{\mathcal{X}_0(p^n,N)_0^{(m)}}^+} \widehat{{\cal O}}_{\mathcal{X}(p^n,N)_0^{(m)}}^+. \end{align*} $$
$$ \begin{align*} Q&:=\omega_E^{\mathrm{mod,-1}} \otimes_{{\cal O}_{\mathcal{X}_0(p^n,N)_0^{(m)}}^+} \widehat{{\cal O}}_{\mathcal{X}(p^n,N)_0^{(m)}}^+ \longrightarrow T_p(E) \otimes_{{\mathbb Z}_p} \widehat{{\cal O}}_{\mathcal{X}(p^n,N)_0^{(m)}}^+\\ &\quad \longrightarrow \omega_E^{\mathrm{mod}}\otimes_{{\cal O}_{\mathcal{X}_0(p^n,N)_0^{(m)}}^+} \widehat{{\cal O}}_{\mathcal{X}(p^n,N)_0^{(m)}}^+. \end{align*} $$
Via the trivialization
![]() $T_p E/p^n T_p E=({\mathbb Z}/p^n{\mathbb Z}) a \oplus ({\mathbb Z}/p^n{\mathbb Z}) b$
over
$T_p E/p^n T_p E=({\mathbb Z}/p^n{\mathbb Z}) a \oplus ({\mathbb Z}/p^n{\mathbb Z}) b$
over
![]() $\mathcal {X}(p^n,N)_0^{(m)}$
, over the component
$\mathcal {X}(p^n,N)_0^{(m)}$
, over the component
![]() $\mathcal {X}(p^n,N)_{0,\xi }^{(m)}$
the canonical subgroup
$\mathcal {X}(p^n,N)_{0,\xi }^{(m)}$
the canonical subgroup
![]() $C_r$
, and hence, Q modulo
$C_r$
, and hence, Q modulo
![]() $p^r$
, is generated by the section
$p^r$
, is generated by the section
![]() $b+\xi a$
and a maps to a generator of the quotient
$b+\xi a$
and a maps to a generator of the quotient
![]() $\omega _E^{\mathrm {mod}}\otimes _{{\cal O}_{\mathcal {X}_0(p,N)_0^{(m)}}^+} \widehat {{\cal O}}_{\mathcal {X}(p^n,N)_0^{(m)}}^+$
modulo
$\omega _E^{\mathrm {mod}}\otimes _{{\cal O}_{\mathcal {X}_0(p,N)_0^{(m)}}^+} \widehat {{\cal O}}_{\mathcal {X}(p^n,N)_0^{(m)}}^+$
modulo
![]() $p^r$
. In particular, we get an affine map
$p^r$
. In particular, we get an affine map
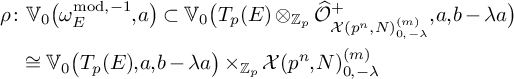 $$ \begin{align*} &\rho\colon {\mathbb V}_0\bigl(\omega_E^{\mathrm{mod,-1}}, a\bigr)\subset {\mathbb V}_0\bigl(T_p(E)\otimes_{{\mathbb Z}_p} \widehat{{\cal O}}_{\mathcal{X}(p^n,N)_{0,-\lambda}^{(m)}}^+, a, b-\lambda a\bigr)\\ &\quad \cong {\mathbb V}_0\bigl(T_p(E) , a, b-\lambda a\bigr) \times_{{\mathbb Z}_p} \mathcal{X}(p^n,N)_{0,-\lambda}^{(m)} \end{align*} $$
$$ \begin{align*} &\rho\colon {\mathbb V}_0\bigl(\omega_E^{\mathrm{mod,-1}}, a\bigr)\subset {\mathbb V}_0\bigl(T_p(E)\otimes_{{\mathbb Z}_p} \widehat{{\cal O}}_{\mathcal{X}(p^n,N)_{0,-\lambda}^{(m)}}^+, a, b-\lambda a\bigr)\\ &\quad \cong {\mathbb V}_0\bigl(T_p(E) , a, b-\lambda a\bigr) \times_{{\mathbb Z}_p} \mathcal{X}(p^n,N)_{0,-\lambda}^{(m)} \end{align*} $$
on the pro-Kummer étale site of
![]() $\mathcal {X}(p^n,N)_{0,-\lambda }^{(m)} $
. Considering the underlying sheaves of functions of weight
$\mathcal {X}(p^n,N)_{0,-\lambda }^{(m)} $
. Considering the underlying sheaves of functions of weight
![]() $0$
, the map
$0$
, the map
![]() $\rho ^{\ast }$
induces a surjective map of sheaves of rings
$\rho ^{\ast }$
induces a surjective map of sheaves of rings
We let
![]() $\mathcal {I}$
be its kernel. We set
$\mathcal {I}$
be its kernel. We set
Taking
![]() $\widehat {{\cal O}}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+$
-duals we get a sheaf and an increasing filtration
$\widehat {{\cal O}}_{\mathcal {X}(p^n,N)_{\infty }^{(m)}}^+$
-duals we get a sheaf and an increasing filtration
on the pro-Kummer étale site of
![]() $\mathcal {X}(p^n,N)_{0,-\lambda }^{(m)}$
. Here,
$\mathcal {X}(p^n,N)_{0,-\lambda }^{(m)}$
. Here,
![]() $\mathrm {Fil}_s \mathfrak {W}_{k,0,\lambda }^{(m),\vee }$
consists of those sections vanishing on
$\mathrm {Fil}_s \mathfrak {W}_{k,0,\lambda }^{(m),\vee }$
consists of those sections vanishing on
![]() $\mathrm {Fil}^s \mathfrak {W}_{k,0,\lambda }^{(m)}$
. Due to Proposition 3.8, we have a
$\mathrm {Fil}^s \mathfrak {W}_{k,0,\lambda }^{(m)}$
. Due to Proposition 3.8, we have a
![]() $\Delta _n$
-equivariant isomorphism
$\Delta _n$
-equivariant isomorphism
and we set
![]() $\mathrm {Fil}_s j_n^{\ast } \bigl ( \mathfrak {D}_{k,\infty }^{o,(m)}[n]\bigr )$
to be the filtration given by
$\mathrm {Fil}_s j_n^{\ast } \bigl ( \mathfrak {D}_{k,\infty }^{o,(m)}[n]\bigr )$
to be the filtration given by
![]() $\oplus _{\lambda \in {\mathbb Z}/p^n{\mathbb Z}} \mathrm {Fil}_s\mathfrak {W}_{k,0,\lambda }^{(m),\vee } $
.
$\oplus _{\lambda \in {\mathbb Z}/p^n{\mathbb Z}} \mathrm {Fil}_s\mathfrak {W}_{k,0,\lambda }^{(m),\vee } $
.
In order to get a well-defined filtration on
![]() $\mathfrak {D}_{k,0}^{o,(m)}[n]$
, we need to prove that
$\mathfrak {D}_{k,0}^{o,(m)}[n]$
, we need to prove that
![]() $\mathrm {Fil}_s j_n^{\ast } \bigl ( \mathfrak {D}_{k,\infty }^{o,(m)}[n]\bigr )$
is
$\mathrm {Fil}_s j_n^{\ast } \bigl ( \mathfrak {D}_{k,\infty }^{o,(m)}[n]\bigr )$
is
![]() $\Delta _n$
-equivariant. If this holds, claim (i) is then clear by construction. Arguing as in Proposition 4.14, to prove claim (ii) it suffices to prove it for
$\Delta _n$
-equivariant. If this holds, claim (i) is then clear by construction. Arguing as in Proposition 4.14, to prove claim (ii) it suffices to prove it for
![]() $\mathrm {H}^1\bigl (\mathcal {X}(p^n,N)_{0,{\mathrm {pke}}}^{(m)}, \_ \,\bigr )$
. As in loc. cit. one reduces the proof of this statement and the statement of the
$\mathrm {H}^1\bigl (\mathcal {X}(p^n,N)_{0,{\mathrm {pke}}}^{(m)}, \_ \,\bigr )$
. As in loc. cit. one reduces the proof of this statement and the statement of the
![]() $\Delta _n$
-equivariance after passing to a log affinoid perfectoid cover U of
$\Delta _n$
-equivariance after passing to a log affinoid perfectoid cover U of
![]() $\mathcal {X}(p^n,N)_{0}^{(m)}$
, with group of automorphisms
$\mathcal {X}(p^n,N)_{0}^{(m)}$
, with group of automorphisms
![]() $G_U$
relatively to
$G_U$
relatively to
![]() $\mathcal {X}_0(p^n,N)_{0}^{(m)}$
and with
$\mathcal {X}_0(p^n,N)_{0}^{(m)}$
and with
![]() $\widehat {U}:=\mathrm {Spa}(R,R^+)$
the associated affinoid perfectoid space. Write
$\widehat {U}:=\mathrm {Spa}(R,R^+)$
the associated affinoid perfectoid space. Write
![]() $T_p(E)(U)\otimes R^+=R^+ f_0 + R^+ f_1$
and
$T_p(E)(U)\otimes R^+=R^+ f_0 + R^+ f_1$
and
![]() $T_p(E)^{\vee }(U)\otimes R^+=e_0 R^+\oplus e_1R^+$
with
$T_p(E)^{\vee }(U)\otimes R^+=e_0 R^+\oplus e_1R^+$
with
![]() $e_0=f_0^{\vee }\equiv b^{\vee }$
mapping to a generator of
$e_0=f_0^{\vee }\equiv b^{\vee }$
mapping to a generator of
![]() $\omega _E^{\mathrm {mod}}$
and
$\omega _E^{\mathrm {mod}}$
and
![]() $e_1=f_1^{\vee }\equiv a^{\vee }-\lambda b^{\vee }$
in the kernel of
$e_1=f_1^{\vee }\equiv a^{\vee }-\lambda b^{\vee }$
in the kernel of
![]() $\mathrm {dlog}$
generating
$\mathrm {dlog}$
generating
![]() $\omega _E^{\mathrm {mod,-1}}$
. Recall from Proposition 3.8 that
$\omega _E^{\mathrm {mod,-1}}$
. Recall from Proposition 3.8 that
![]() $\mathfrak {W}_{k,0,\lambda }^{(m),\vee }(U)$
is the dual of
$\mathfrak {W}_{k,0,\lambda }^{(m),\vee }(U)$
is the dual of
![]() $\mathfrak {W}_{k,0,\lambda }^{(m)}(U)\cong (R^+\otimes B)\langle \frac {W_{\lambda }}{1+p^r Z} \rangle \cdot k(1+p^r Z)$
where
$\mathfrak {W}_{k,0,\lambda }^{(m)}(U)\cong (R^+\otimes B)\langle \frac {W_{\lambda }}{1+p^r Z} \rangle \cdot k(1+p^r Z)$
where
![]() $p^r W_{\lambda }= Y$
and
$p^r W_{\lambda }= Y$
and
![]() $X=1+p^r Z$
, and we have the universal map
$X=1+p^r Z$
, and we have the universal map
![]() $\alpha f_0 + \beta f_1\mapsto \alpha Y +\beta X$
(note the roles of X and Y are interchanged compared to loc. cit. as in this case we are looking for functions on T that are
$\alpha f_0 + \beta f_1\mapsto \alpha Y +\beta X$
(note the roles of X and Y are interchanged compared to loc. cit. as in this case we are looking for functions on T that are
![]() $0$
on b modulo
$0$
on b modulo
![]() $p^r$
and
$p^r$
and
![]() $1$
on a modulo
$1$
on a modulo
![]() $p^r$
, or equivalently that are
$p^r$
, or equivalently that are
![]() $1$
on
$1$
on
![]() $e_1$
modulo
$e_1$
modulo
![]() $p^r$
and
$p^r$
and
![]() $0$
on
$0$
on
![]() $e_0-\lambda e_1$
modulo
$e_0-\lambda e_1$
modulo
![]() $p^r$
). The decreasing filtration is defined by
$p^r$
). The decreasing filtration is defined by
![]() $\mathrm {Fil}^s = \oplus _{i\geq s}(R^+\otimes B) \bigl (\frac {W_{\lambda }}{1+p^r Z}\bigr )^i \cdot k(1+p^r Z) $
.
$\mathrm {Fil}^s = \oplus _{i\geq s}(R^+\otimes B) \bigl (\frac {W_{\lambda }}{1+p^r Z}\bigr )^i \cdot k(1+p^r Z) $
.
Given
![]() $\sigma \in G_U$
, we have
$\sigma \in G_U$
, we have
![]() $\sigma (e_0)=e_0$
and
$\sigma (e_0)=e_0$
and
![]() $\sigma (e_1)=e_1+ \xi (\sigma ) e_0$
so that
$\sigma (e_1)=e_1+ \xi (\sigma ) e_0$
so that
![]() $\sigma (Y)=Y$
and
$\sigma (Y)=Y$
and
![]() $\sigma (X)=X+\xi (\sigma ) Y= X+ p^r \xi (\sigma ) W_{\lambda }$
. Here,
$\sigma (X)=X+\xi (\sigma ) Y= X+ p^r \xi (\sigma ) W_{\lambda }$
. Here,
![]() $\xi $
is an
$\xi $
is an
![]() $R^+$
-valued continuous
$R^+$
-valued continuous
![]() $1$
-cocycle on
$1$
-cocycle on
![]() $G_U$
. In particular, write
$G_U$
. In particular, write
![]() $k(t)=\exp (u_k \log (t))$
for
$k(t)=\exp (u_k \log (t))$
for
![]() $t\equiv 1$
modulo
$t\equiv 1$
modulo
![]() $p^r$
. Then
$p^r$
. Then
 $$ \begin{align*} =k(X) X^{-i} \exp\bigl((u_k-i) \log(1+ p^r \xi(\sigma) \frac{W_{\lambda}}{X})\bigr)=k(X) X^{-i} \sum_{m=0}^{\infty} p^{r m} \left(\begin{matrix} u_k-i \cr m \end{matrix}\right)\bigl(\xi(\sigma) \frac{W_{\lambda}}{X}\bigr)^m.\\[-9pt] \end{align*} $$
$$ \begin{align*} =k(X) X^{-i} \exp\bigl((u_k-i) \log(1+ p^r \xi(\sigma) \frac{W_{\lambda}}{X})\bigr)=k(X) X^{-i} \sum_{m=0}^{\infty} p^{r m} \left(\begin{matrix} u_k-i \cr m \end{matrix}\right)\bigl(\xi(\sigma) \frac{W_{\lambda}}{X}\bigr)^m.\\[-9pt] \end{align*} $$
Notice that the term
![]() $m=0$
is
$m=0$
is
![]() $(u_k-i) k(X) X^{-i}$
. Thus,
$(u_k-i) k(X) X^{-i}$
. Thus,
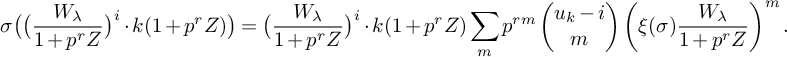 $$ \begin{align} \sigma\bigl(\bigl(\frac{W_{\lambda}}{1+p^r Z}\bigr)^i \cdot k(1+p^r Z) \bigr)=\bigl(\frac{W_{\lambda}}{1+p^r Z}\bigr)^i \cdot k(1+p^r Z) \sum_{m} p^{r m} \left(\begin{matrix} u_k-i \cr m \end{matrix}\right)\left(\xi(\sigma) \frac{W_{\lambda}}{1+p^r Z}\right)^m.\\[-9pt]\nonumber \end{align} $$
$$ \begin{align} \sigma\bigl(\bigl(\frac{W_{\lambda}}{1+p^r Z}\bigr)^i \cdot k(1+p^r Z) \bigr)=\bigl(\frac{W_{\lambda}}{1+p^r Z}\bigr)^i \cdot k(1+p^r Z) \sum_{m} p^{r m} \left(\begin{matrix} u_k-i \cr m \end{matrix}\right)\left(\xi(\sigma) \frac{W_{\lambda}}{1+p^r Z}\right)^m.\\[-9pt]\nonumber \end{align} $$
This implies first of all that
![]() $G_U$
preserves the filtration. Claim (ii) follows from the following lemma.
$G_U$
preserves the filtration. Claim (ii) follows from the following lemma.
Lemma 4.17. For every s, consider the short exact sequence of
![]() $G_U$
-modules
$G_U$
-modules
Then, the connecting homomorphism
has cokernel annihilated by
 $p^{(r+c) s}s! \left (\begin {matrix} u_k \cr s \end {matrix} \right ) $
for some c depending on n.
$p^{(r+c) s}s! \left (\begin {matrix} u_k \cr s \end {matrix} \right ) $
for some c depending on n.
Proof. We argue by induction on s. We are reduced to prove that for any s the short exact sequence
the connecting homomorphism
has cokernel annihilated by
![]() $p^{(r+c)} \frac {(u_k- s)}{s} $
for some c depending on n. Note that
$p^{(r+c)} \frac {(u_k- s)}{s} $
for some c depending on n. Note that
 $$ \begin{align*}\mathrm{H}^0\bigl( G_U, \mathrm{Gr}_{s+1}\mathfrak{W}_{k,0,\lambda}^{(m)}(U) \bigr)=\bigl((R^+)^{G_U} \otimes B\bigr) \left(\Bigl(\frac{W_{\lambda}}{1+p^r Z}\Bigr)^{s+1} \cdot k(1+p^r Z)\right)^{\vee} \end{align*} $$
$$ \begin{align*}\mathrm{H}^0\bigl( G_U, \mathrm{Gr}_{s+1}\mathfrak{W}_{k,0,\lambda}^{(m)}(U) \bigr)=\bigl((R^+)^{G_U} \otimes B\bigr) \left(\Bigl(\frac{W_{\lambda}}{1+p^r Z}\Bigr)^{s+1} \cdot k(1+p^r Z)\right)^{\vee} \end{align*} $$
and
 $$ \begin{align*} \mathrm{H}^1\!\bigl(G_U, \mathrm{Gr}_{s} \mathfrak{W}_{k,0,\lambda}^{(m)}(U)\!\bigr)&=\bigl(\!(R^+)^{G_U} \otimes B\bigr)\! \otimes_{(R^+)^{G_U}} \!\left(\!\Bigl(\!\frac{W_{\lambda}}{1+p^r Z}\!\Bigr)^s \cdot k(1+p^r Z)\!\right)^{\vee} \mathrm{H}^1\bigl(G_U, R^+\bigr). \end{align*} $$
$$ \begin{align*} \mathrm{H}^1\!\bigl(G_U, \mathrm{Gr}_{s} \mathfrak{W}_{k,0,\lambda}^{(m)}(U)\!\bigr)&=\bigl(\!(R^+)^{G_U} \otimes B\bigr)\! \otimes_{(R^+)^{G_U}} \!\left(\!\Bigl(\!\frac{W_{\lambda}}{1+p^r Z}\!\Bigr)^s \cdot k(1+p^r Z)\!\right)^{\vee} \mathrm{H}^1\bigl(G_U, R^+\bigr). \end{align*} $$
Thanks to equation (7), the map sends
 $\left (\Bigl (\frac {W_{\lambda }}{1+p^r Z}\Bigr )^{s+1} \cdot k(1+p^r Z)\right )^{\vee } $
to the cocyle
$\left (\Bigl (\frac {W_{\lambda }}{1+p^r Z}\Bigr )^{s+1} \cdot k(1+p^r Z)\right )^{\vee } $
to the cocyle
![]() $G_U\ni \sigma \mapsto (u_k-s) p^r \xi (\sigma ) \left (\Bigl (\frac {W_{\lambda }}{1+p^r Z}\Bigr )^s \cdot k(1+p^r Z)\right )^{\vee } $
. The quotient of
$G_U\ni \sigma \mapsto (u_k-s) p^r \xi (\sigma ) \left (\Bigl (\frac {W_{\lambda }}{1+p^r Z}\Bigr )^s \cdot k(1+p^r Z)\right )^{\vee } $
. The quotient of
![]() $ \mathrm {H}^1\bigl (G_U, R^+\bigr )$
by the
$ \mathrm {H}^1\bigl (G_U, R^+\bigr )$
by the
![]() $(R^+)^{G_U}$
-span of the cocycle
$(R^+)^{G_U}$
-span of the cocycle
![]() $\xi $
is torsion and hence killed by a power
$\xi $
is torsion and hence killed by a power
![]() $p^c$
of p; see [Reference Andreatta, Iovita and Stevens6, Prop. 5.2]. The conclusion follows.
$p^c$
of p; see [Reference Andreatta, Iovita and Stevens6, Prop. 5.2]. The conclusion follows.
5 The Hodge–Tate Eichler–Shimura map revisited
Let
![]() $k\colon {\mathbb Z}_p^{\ast }\longrightarrow B^{\ast }$
be a B-valued weight, as in Definition 3.6, which is r-analytic for some
$k\colon {\mathbb Z}_p^{\ast }\longrightarrow B^{\ast }$
be a B-valued weight, as in Definition 3.6, which is r-analytic for some
![]() $r\in {\mathbb N}$
(definition 3.6), that is, there is
$r\in {\mathbb N}$
(definition 3.6), that is, there is
![]() $u_k\in B[1/p]$
such that
$u_k\in B[1/p]$
such that
![]() $k(t)=\mathrm {exp}\bigl (u_k\log (t)\bigr )$
for all
$k(t)=\mathrm {exp}\bigl (u_k\log (t)\bigr )$
for all
![]() $t\in 1+p^{r}{\mathbb Z}_p$
. In this section, we fix an integer
$t\in 1+p^{r}{\mathbb Z}_p$
. In this section, we fix an integer
![]() $n\ge r$
and denote
$n\ge r$
and denote
![]() ${\mathbb D}^o_k(T_0^{\vee })[n]$
the integral pro-Kummer étale sheaf of distributions on the base-change of
${\mathbb D}^o_k(T_0^{\vee })[n]$
the integral pro-Kummer étale sheaf of distributions on the base-change of
![]() $\mathcal {X}:=\mathcal {X}_0(p^n, N)$
over
$\mathcal {X}:=\mathcal {X}_0(p^n, N)$
over
![]() $\mathrm {Spa}(B[1/p], B)$
. We will simply denote this sheaf by
$\mathrm {Spa}(B[1/p], B)$
. We will simply denote this sheaf by
![]() ${\mathbb D}^o_k$
in this section and also set
${\mathbb D}^o_k$
in this section and also set
![]() ${\mathbb D}_k:={\mathbb D}_k^o\otimes _{{\mathbb Z}_p}{\mathbb Q}_p$
.
${\mathbb D}_k:={\mathbb D}_k^o\otimes _{{\mathbb Z}_p}{\mathbb Q}_p$
.
Let us fix a slope
![]() $h\in {\mathbb N}$
, and recall that if M is a
$h\in {\mathbb N}$
, and recall that if M is a
![]() ${\mathbb Q}_p$
-vector space with a linear endomorphism
${\mathbb Q}_p$
-vector space with a linear endomorphism
![]() $U_p$
, we denote
$U_p$
, we denote
![]() $M^{(h)}$
the subvector space of M of elements
$M^{(h)}$
the subvector space of M of elements
![]() $x\in M$
such that
$x\in M$
such that
![]() $P(U_p)(x)=0$
for all polynomials
$P(U_p)(x)=0$
for all polynomials
![]() $P(X)\in {\mathbb Q}_p[X]$
, whose roots in
$P(X)\in {\mathbb Q}_p[X]$
, whose roots in
![]() ${\mathbb C}_p$
have all valuations in
${\mathbb C}_p$
have all valuations in
![]() $[0,h]\cap {\mathbb Q}$
. Up to localization of B and for s large enough, both
$[0,h]\cap {\mathbb Q}$
. Up to localization of B and for s large enough, both
![]() $\mathrm { H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}_k \bigr )$
and
$\mathrm { H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}_k \bigr )$
and
![]() $\mathrm {H}^0\bigl (\mathcal {X}\langle \frac {p}{\mathrm {Ha}^{p^s}} \rangle , \omega _E^{k+2}\bigr )$
admit slope h decompositions; here,
$\mathrm {H}^0\bigl (\mathcal {X}\langle \frac {p}{\mathrm {Ha}^{p^s}} \rangle , \omega _E^{k+2}\bigr )$
admit slope h decompositions; here,
![]() $\mathrm {Ha}$
is a (any) local lift of the Hasse invariant. Then the main result of this section is as follows.
$\mathrm {Ha}$
is a (any) local lift of the Hasse invariant. Then the main result of this section is as follows.
Theorem 5.1. For s large enough, there is a canonical
![]() ${\mathbb C}_p$
-linear, Galois and Hecke equivariant map:
${\mathbb C}_p$
-linear, Galois and Hecke equivariant map:
Moreover, if
![]() $\prod _{i=0}^{h-1}(u_k-i)\in \bigl (B[1/p] \bigr )^{\ast }$
, then
$\prod _{i=0}^{h-1}(u_k-i)\in \bigl (B[1/p] \bigr )^{\ast }$
, then
![]() $\Psi _{\mathrm {HT}}$
is surjective.
$\Psi _{\mathrm {HT}}$
is surjective.
The map
![]() $\Psi _{\mathrm {HT}}$
was defined in [Reference Andreatta, Iovita and Stevens5] using Faltings’ sites of
$\Psi _{\mathrm {HT}}$
was defined in [Reference Andreatta, Iovita and Stevens5] using Faltings’ sites of
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {X}\langle \frac {p}{\mathrm {Ha}^{p^s}} \rangle $
, respectively. To relate it to the language developed in this paper, first of all we allow ourselves to increase n. In fact, the map
$\mathcal {X}\langle \frac {p}{\mathrm {Ha}^{p^s}} \rangle $
, respectively. To relate it to the language developed in this paper, first of all we allow ourselves to increase n. In fact, the map
![]() $\mathcal {X}_0(p^{n_1},N)\to \mathcal {X}_0(p^{n_2},N)$
for
$\mathcal {X}_0(p^{n_1},N)\to \mathcal {X}_0(p^{n_2},N)$
for
![]() $n_1\geq n_2$
is finite étale, and one can obtain the map
$n_1\geq n_2$
is finite étale, and one can obtain the map
![]() $\Psi _{\mathrm {HT}}$
for
$\Psi _{\mathrm {HT}}$
for
![]() $n=n_1$
in the theorem upon taking traces from the map
$n=n_1$
in the theorem upon taking traces from the map
![]() $\Psi _{\mathrm {HT}}$
for
$\Psi _{\mathrm {HT}}$
for
![]() $n=n_2$
; on the left-hand side the trace is defined using Lemma 4.7. We also replace
$n=n_2$
; on the left-hand side the trace is defined using Lemma 4.7. We also replace
![]() $\mathcal {X}_0(p^n,N)\langle \frac {p}{\mathrm {Ha}^{p^s}} \rangle $
with
$\mathcal {X}_0(p^n,N)\langle \frac {p}{\mathrm {Ha}^{p^s}} \rangle $
with
![]() $\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
for arbitrary large integers
$\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
for arbitrary large integers
![]() $n\geq m$
, as the first is contained in the latter for m large enough thanks to [Reference Scholze23, Lemma 3.3.15].
$n\geq m$
, as the first is contained in the latter for m large enough thanks to [Reference Scholze23, Lemma 3.3.15].
In particular, we choose n large enough such that there is
![]() $m\le n$
with the property that the restriction of
$m\le n$
with the property that the restriction of
![]() ${\mathbb D}_k^o$
to the pro-Kummer étale site of
${\mathbb D}_k^o$
to the pro-Kummer étale site of
![]() $\mathcal {X}_0(p^n, N)_{\infty }^{(m)}$
has the property that the (pro-Kummer étale) sheaf
$\mathcal {X}_0(p^n, N)_{\infty }^{(m)}$
has the property that the (pro-Kummer étale) sheaf
![]() ${\mathbb D}_k^o\widehat {\otimes }\widehat {{\cal O}}_{\mathcal {X}_0(p^n, N)_{\infty }^{(m)}}$
has the decreasing filtration defined in Proposition 4.14. We fix such n, m. Let us denote by
${\mathbb D}_k^o\widehat {\otimes }\widehat {{\cal O}}_{\mathcal {X}_0(p^n, N)_{\infty }^{(m)}}$
has the decreasing filtration defined in Proposition 4.14. We fix such n, m. Let us denote by
![]() ${\mathfrak {D}}_k^o:={\mathbb D}_k^o\widehat {\otimes }{\cal O}_{\mathcal {X}_{\mathrm {pke}}}^+$
, where
${\mathfrak {D}}_k^o:={\mathbb D}_k^o\widehat {\otimes }{\cal O}_{\mathcal {X}_{\mathrm {pke}}}^+$
, where
![]() ${\cal O}_{\mathcal {X}_{\mathrm {pke}}}^+$
is the structure sheaf of the pro-Kummer étal site of
${\cal O}_{\mathcal {X}_{\mathrm {pke}}}^+$
is the structure sheaf of the pro-Kummer étal site of
![]() $\mathcal {X}$
. As in [Reference Andreatta, Iovita and Stevens5], we let
$\mathcal {X}$
. As in [Reference Andreatta, Iovita and Stevens5], we let
![]() $\Psi _{\mathrm {HT}}$
be the composition of the following maps:
$\Psi _{\mathrm {HT}}$
be the composition of the following maps:
where
![]() $\mathcal {R}$
is the restriction map while the map
$\mathcal {R}$
is the restriction map while the map
![]() $\Phi $
is defined in Proposition 4.15 and it is proved in loc. cit. that it is an isomorphism. Therefore, in order to prove Theorem 5.1, it is enough to prove the following.
$\Phi $
is defined in Proposition 4.15 and it is proved in loc. cit. that it is an isomorphism. Therefore, in order to prove Theorem 5.1, it is enough to prove the following.
Theorem 5.2. In the notations above, if
![]() $\prod _{i=0}^{h-1}(u_k-i)\in \bigl (B[1/p] \bigr )^{\ast }$
, then the map
$\prod _{i=0}^{h-1}(u_k-i)\in \bigl (B[1/p] \bigr )^{\ast }$
, then the map
![]() $\mathcal {R}$
is surjective.
$\mathcal {R}$
is surjective.
To simplify the notation, in the rest of the section, we write
![]() $\mathcal {X}$
instead of
$\mathcal {X}$
instead of
![]() $\mathcal {X}_0(p^n, N)$
,
$\mathcal {X}_0(p^n, N)$
,
![]() $\mathcal {X}_{\infty }^{(m)}$
instead of
$\mathcal {X}_{\infty }^{(m)}$
instead of
![]() $\mathcal {X}_0(p^n, N)_{\infty }^{(m)}$
, and so on. Before starting the proof of Theorem 5.2, we’ll describe the dynamic of the
$\mathcal {X}_0(p^n, N)_{\infty }^{(m)}$
, and so on. Before starting the proof of Theorem 5.2, we’ll describe the dynamic of the
![]() $U_p$
-operator on the modular curve
$U_p$
-operator on the modular curve
![]() $\mathcal {X}$
. We think about
$\mathcal {X}$
. We think about
![]() $U_p$
as correspondences on
$U_p$
as correspondences on
![]() $\mathcal {X}$
, and we have:
$\mathcal {X}$
, and we have:
Lemma 5.3. For every integer
![]() $u\ge 1$
, we have
$u\ge 1$
, we have
-
i)
 $U_p^{u+1}\bigl (\mathcal {X}\backslash \mathcal {X}_0^{(u+1)}\bigr )\subset \mathcal {X}_{\infty }^{(1)}$
and
$U_p^{u+1}\bigl (\mathcal {X}\backslash \mathcal {X}_0^{(u+1)}\bigr )\subset \mathcal {X}_{\infty }^{(1)}$
and
 $U_p^u(\mathcal {X}\backslash \mathcal {X}_0^{(u+1)})\subset \mathcal {X}_{\infty }\backslash \mathcal {X}_0^{(1)}$
.
$U_p^u(\mathcal {X}\backslash \mathcal {X}_0^{(u+1)})\subset \mathcal {X}_{\infty }\backslash \mathcal {X}_0^{(1)}$
. -
ii)
 $U_p^{u}\bigl (\mathcal {X}_{\infty }^{(1)} \bigr ) \subset \mathcal {X}_{\infty }^{(u+1)}$
.
$U_p^{u}\bigl (\mathcal {X}_{\infty }^{(1)} \bigr ) \subset \mathcal {X}_{\infty }^{(u+1)}$
.
Proof. This is a direct consequence of Lemma 4.9.
We also have:
Lemma 5.4. For every
![]() $u\ge 1$
, there is a canonical decomposition of correspondences
$u\ge 1$
, there is a canonical decomposition of correspondences
![]() $U_p^u|_{\mathcal {X}_0^{(u)}}=\bigl (U_p^u\bigr )^{\mathrm {good}}\amalg \bigl (U_p^u \bigr )^{\mathrm {bad}}$
such that:
$U_p^u|_{\mathcal {X}_0^{(u)}}=\bigl (U_p^u\bigr )^{\mathrm {good}}\amalg \bigl (U_p^u \bigr )^{\mathrm {bad}}$
such that:
-
a)
 $(U_p^u)^{\mathrm {good}}\bigl (\mathcal {X}_0^{(u)}\bigr )\subset \mathcal {X}_{\infty }^{(1)}.$
$(U_p^u)^{\mathrm {good}}\bigl (\mathcal {X}_0^{(u)}\bigr )\subset \mathcal {X}_{\infty }^{(1)}.$
-
b)
 $(U_p^u)^{\mathrm {bad}}\bigl (\mathcal {X}_0^{(u)} \backslash \mathcal {X}_0^{(u+1)} \bigr )\subset \mathcal {X}_{\infty }\backslash \mathcal {X}_0^{(1)}$
.
$(U_p^u)^{\mathrm {bad}}\bigl (\mathcal {X}_0^{(u)} \backslash \mathcal {X}_0^{(u+1)} \bigr )\subset \mathcal {X}_{\infty }\backslash \mathcal {X}_0^{(1)}$
.
We remark that for
![]() $u=1$
,
$u=1$
,
![]() $U_p^1 =U_p$
and so we obtain the decomposition of
$U_p^1 =U_p$
and so we obtain the decomposition of
![]() $U_p|_{\mathcal {X}_0{(1)}}=\bigl (U_p\bigr )^{\mathrm {good}}\amalg \bigl (U_p \bigr )^{\mathrm {bad}}$
.
$U_p|_{\mathcal {X}_0{(1)}}=\bigl (U_p\bigr )^{\mathrm {good}}\amalg \bigl (U_p \bigr )^{\mathrm {bad}}$
.
Proof. In view of Lemma 4.9 and Remark 4.8, it is enough to define this decomposition for the correspondence
![]() $\widetilde {U}^u:=\cup _{\mu }t_{\mu }\colon U_0^{(u)}\longrightarrow \mathcal {P}\bigl ({\mathbb P}^1\bigr )$
, where
$\widetilde {U}^u:=\cup _{\mu }t_{\mu }\colon U_0^{(u)}\longrightarrow \mathcal {P}\bigl ({\mathbb P}^1\bigr )$
, where
![]() $\mu =\lambda _0+\lambda _1p+\ldots +\lambda _{u-1}p^{u-1}$
,
$\mu =\lambda _0+\lambda _1p+\ldots +\lambda _{u-1}p^{u-1}$
,
![]() $\lambda _i\in \{0,1,\ldots ,p-1\}$
, for
$\lambda _i\in \{0,1,\ldots ,p-1\}$
, for
![]() $i=0,1,\ldots ,u-1.$
Namely, we define
$i=0,1,\ldots ,u-1.$
Namely, we define
![]() $(\widetilde {U}^u)^{\mathrm {bad}}\vert _{U_{0,\mu }^{(u)}}:=t_{\mu }$
and
$(\widetilde {U}^u)^{\mathrm {bad}}\vert _{U_{0,\mu }^{(u)}}:=t_{\mu }$
and
![]() $(\widetilde {U}^u)^{\mathrm {good}}\vert _{U_{0,\mu }^{(u)}}:=\cup _{\lambda \neq \mu }t_{\lambda }$
. With these definitions, the rest of Lemma 5.4 follows from Lemma 4.9.
$(\widetilde {U}^u)^{\mathrm {good}}\vert _{U_{0,\mu }^{(u)}}:=\cup _{\lambda \neq \mu }t_{\lambda }$
. With these definitions, the rest of Lemma 5.4 follows from Lemma 4.9.
We have the following consequence of Lemma 5.3 and Lemma 5.4. Let us recall our notation
![]() ${\mathfrak {D}}_k^o:={\mathbb D}_k^o\widehat {\otimes }{\cal O}^+_{\mathcal {X}}$
(this is a sheaf on the pro-Kummer étale site of the base-change of
${\mathfrak {D}}_k^o:={\mathbb D}_k^o\widehat {\otimes }{\cal O}^+_{\mathcal {X}}$
(this is a sheaf on the pro-Kummer étale site of the base-change of
![]() $\mathcal {X}$
to
$\mathcal {X}$
to
![]() $\mathrm {Spa}(B[1/p], B)$
) base-change which is not shown in the notations. Also, we recall that we use the operator
$\mathrm {Spa}(B[1/p], B)$
) base-change which is not shown in the notations. Also, we recall that we use the operator
![]() $U_p^{\mathrm {naive}}$
induced on cohomology by the
$U_p^{\mathrm {naive}}$
induced on cohomology by the
![]() $U_p$
-correspondence and not its normalized version
$U_p$
-correspondence and not its normalized version
![]() $p^{-1} U_p^{\mathrm { naive}}$
. With this understanding, to ease the notation, we simply write
$p^{-1} U_p^{\mathrm { naive}}$
. With this understanding, to ease the notation, we simply write
![]() $U_p$
instead of
$U_p$
instead of
![]() $U_p^{\mathrm {naive}}$
.
$U_p^{\mathrm {naive}}$
.
Corollary 5.5. Let
![]() $P(T)\in (B\widehat {\otimes }{\cal O}_{{\mathbb C}_p})[T]$
be such that
$P(T)\in (B\widehat {\otimes }{\cal O}_{{\mathbb C}_p})[T]$
be such that
![]() $P(T)=TR(T)$
and for every
$P(T)=TR(T)$
and for every
![]() $u\ge 1$
denote
$u\ge 1$
denote
![]() $\bigl (P(U_p)^u \bigr )^{\mathrm { good}}:=(U_p^u)^{\mathrm {good}}R(U_p)^u$
and
$\bigl (P(U_p)^u \bigr )^{\mathrm { good}}:=(U_p^u)^{\mathrm {good}}R(U_p)^u$
and
![]() $\bigl (P(U_p)^u\bigr )^{\mathrm {bad}}:=\big (U_p^u)^{\mathrm {bad}}R(U_p)^u$
. Then
$\bigl (P(U_p)^u\bigr )^{\mathrm {bad}}:=\big (U_p^u)^{\mathrm {bad}}R(U_p)^u$
. Then
-
i)
 $P(U_p)^{u}\colon \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )\longrightarrow \mathrm { H}^1\bigl ((\mathcal {X}\backslash \mathcal {X}_0^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )$
.
$P(U_p)^{u}\colon \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )\longrightarrow \mathrm { H}^1\bigl ((\mathcal {X}\backslash \mathcal {X}_0^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )$
. -
ii)
 $P(U_p)^{u-1}\colon \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )\longrightarrow \mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )$
.
$P(U_p)^{u-1}\colon \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )\longrightarrow \mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )$
. -
iii)
 $\bigl (P(U_p)^u\bigr )^{\mathrm {good}}P(U_p)\colon \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }\backslash \mathcal {X}_0^{(1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o\bigr ) \longrightarrow \mathrm {H}^1\bigl ( (\mathcal {X}_0^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )$
.
$\bigl (P(U_p)^u\bigr )^{\mathrm {good}}P(U_p)\colon \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }\backslash \mathcal {X}_0^{(1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o\bigr ) \longrightarrow \mathrm {H}^1\bigl ( (\mathcal {X}_0^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )$
. -
iv)
 $\bigl (P(U_p)^u\bigr )^{\mathrm {bad}}\colon \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }\backslash \mathcal {X}_0^{(1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o\bigr ) \longrightarrow \mathrm {H}^1\bigl ( (\mathcal {X}_0^{(u)} \backslash \mathcal {X}_0^{(u+1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )$
.
$\bigl (P(U_p)^u\bigr )^{\mathrm {bad}}\colon \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }\backslash \mathcal {X}_0^{(1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o\bigr ) \longrightarrow \mathrm {H}^1\bigl ( (\mathcal {X}_0^{(u)} \backslash \mathcal {X}_0^{(u+1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )$
.
Proof. In view of the fact that, for any polynomial
![]() $Q(T)$
with
$Q(T)$
with
![]() $(B\widehat {\otimes }{\cal O}_{{\mathbb C}_p})$
-coeffcients,
$(B\widehat {\otimes }{\cal O}_{{\mathbb C}_p})$
-coeffcients,
![]() $Q(U_p)$
maps
$Q(U_p)$
maps
![]() $\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )$
to itself, i) and, respectively, ii) are immediate consequences of Lemma 5.3 a) and b), respectively, while iii) is a consequence of Lemma 5.4 a) and iii) follows from Lemma 5.4 b).
$\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(1)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )$
to itself, i) and, respectively, ii) are immediate consequences of Lemma 5.3 a) and b), respectively, while iii) is a consequence of Lemma 5.4 a) and iii) follows from Lemma 5.4 b).
Before we start the actual proof of Theorem 5.2, it seems natural to recall and gather here the main ingredients in the proof, namely the properties of the cohomology of the filtrations of the sheaf
![]() ${\mathfrak {D}}_k^o$
on
${\mathfrak {D}}_k^o$
on
![]() $\mathcal {X}_{\infty }^{(m)}$
and respectively on
$\mathcal {X}_{\infty }^{(m)}$
and respectively on
![]() $\mathcal {X}_0^{(v)}$
, for m as fixed at the beginning of this section and for the moment
$\mathcal {X}_0^{(v)}$
, for m as fixed at the beginning of this section and for the moment
![]() $v\ge 1$
such that the pro-Kummer étale sheaf
$v\ge 1$
such that the pro-Kummer étale sheaf
![]() ${\mathfrak {D}}_k^o$
has the increasing filtration
${\mathfrak {D}}_k^o$
has the increasing filtration
![]() ${\mathfrak {Fil}}_{\bullet }$
of Proposition 4.16 when restricted to
${\mathfrak {Fil}}_{\bullet }$
of Proposition 4.16 when restricted to
![]() $\mathcal {X}_0^{(v)}$
.
$\mathcal {X}_0^{(v)}$
.
Recall that we have denoted by
![]() ${\mathfrak {D}}^o_k:={\mathbb D}^o_k\widehat {\otimes }\widehat {{\cal O}}^+_{\mathcal {X}}$
for
${\mathfrak {D}}^o_k:={\mathbb D}^o_k\widehat {\otimes }\widehat {{\cal O}}^+_{\mathcal {X}}$
for
![]() $\widehat {{\cal O}}^+_{\mathcal {X}}$
the completion of the structure sheaf of the pro-Kummer étale site of
$\widehat {{\cal O}}^+_{\mathcal {X}}$
the completion of the structure sheaf of the pro-Kummer étale site of
![]() $\mathcal {X}$
. We have:
$\mathcal {X}$
. We have:
i) The image of the morphism
![]() $\mathrm {H}^1\bigl ((\mathcal {X}^{(v)}_0)_{{\mathrm {pke}}}, {\mathfrak {Fil}}_h\bigr )\longrightarrow \mathrm { H}^1\bigl ((\mathcal {X}^{(v)}_0)_{{\mathrm {pke}}}, {\mathfrak {D}}_k^o \bigr )$
is annihilated by
$\mathrm {H}^1\bigl ((\mathcal {X}^{(v)}_0)_{{\mathrm {pke}}}, {\mathfrak {Fil}}_h\bigr )\longrightarrow \mathrm { H}^1\bigl ((\mathcal {X}^{(v)}_0)_{{\mathrm {pke}}}, {\mathfrak {D}}_k^o \bigr )$
is annihilated by
![]() $p^{(r+c)h}\prod _{i=0}^{h-1}(u_k-i)/h!$
, where let us recall r is the degree of analyticity of the weight on B,
$p^{(r+c)h}\prod _{i=0}^{h-1}(u_k-i)/h!$
, where let us recall r is the degree of analyticity of the weight on B,
![]() $\mathcal {X}=\mathcal {X}_0(p^n, N)$
and c is constant independent of h. In particular, if
$\mathcal {X}=\mathcal {X}_0(p^n, N)$
and c is constant independent of h. In particular, if
![]() $\Bigl (\prod _{i=0}^{h-1}(u_k-i)/h!\Bigr )\gamma =p^q$
for some
$\Bigl (\prod _{i=0}^{h-1}(u_k-i)/h!\Bigr )\gamma =p^q$
for some
![]() $\gamma \in B$
, then
$\gamma \in B$
, then
![]() $p^{(r+c)h+q}$
annihilates the image of the above map.
$p^{(r+c)h+q}$
annihilates the image of the above map.
ii) The
![]() $U_p$
correspondence on
$U_p$
correspondence on
![]() $\mathcal {X}_0^{(m)}$
can be written as the disjoint union of
$\mathcal {X}_0^{(m)}$
can be written as the disjoint union of
![]() $U_p^{\mathrm {good}}$
, mapping
$U_p^{\mathrm {good}}$
, mapping
![]() $\mathcal {X}_0^{(m)}$
to
$\mathcal {X}_0^{(m)}$
to
![]() $\mathcal {X}_{\infty }^{(1)}$
and
$\mathcal {X}_{\infty }^{(1)}$
and
![]() $U_p^{\mathrm {bad}}\colon \mathcal {X}_0^{(m)}\to \mathcal {X}_0^{(m-1)}$
and corresponding to the p-isogeny
$U_p^{\mathrm {bad}}\colon \mathcal {X}_0^{(m)}\to \mathcal {X}_0^{(m-1)}$
and corresponding to the p-isogeny
![]() $E \to E'$
given by modding out by the canonical subgroup. To keep track of where our sheaves are defined, we denote
$E \to E'$
given by modding out by the canonical subgroup. To keep track of where our sheaves are defined, we denote
![]() $\mathfrak {D}_{k,0}^{o,(s)}$
the restriction of the pro-Kummer étale sheaf
$\mathfrak {D}_{k,0}^{o,(s)}$
the restriction of the pro-Kummer étale sheaf
![]() $\mathfrak {D}^o_k$
to
$\mathfrak {D}^o_k$
to
![]() $(\mathcal {X}_0^{(s)})_{\mathrm {pke}}$
. Suppose
$(\mathcal {X}_0^{(s)})_{\mathrm {pke}}$
. Suppose
![]() $1\le u\le m$
is such that
$1\le u\le m$
is such that
![]() ${\mathfrak {D}}_{0,k}^{o,(u-1)}$
has the increasing filtration
${\mathfrak {D}}_{0,k}^{o,(u-1)}$
has the increasing filtration
![]() $\mathfrak {Fil}_{\bullet }^{(u-1)}$
on
$\mathfrak {Fil}_{\bullet }^{(u-1)}$
on
![]() $(\mathcal {X}_0^{(u-1)})_{\mathrm {pke}}$
. We have:
$(\mathcal {X}_0^{(u-1)})_{\mathrm {pke}}$
. We have:
Proposition 5.6. The map
![]() $U_p^{\mathrm {bad}}$
induces a map
$U_p^{\mathrm {bad}}$
induces a map
![]() $U_p^{\mathrm {bad}}\colon \mathfrak {D}_{k,0}^{o,(u)} \to \gamma ^{\ast } \bigl (\mathfrak {D}_{k,0}^{o,(u-1)} \bigr ) $
that preserves the filtration. Furthermore, for every b, there exists an operator
$U_p^{\mathrm {bad}}\colon \mathfrak {D}_{k,0}^{o,(u)} \to \gamma ^{\ast } \bigl (\mathfrak {D}_{k,0}^{o,(u-1)} \bigr ) $
that preserves the filtration. Furthermore, for every b, there exists an operator
such that
![]() $U_p^{\mathrm {bad}}=p^b U_p^{\mathrm {bad,b}}$
on
$U_p^{\mathrm {bad}}=p^b U_p^{\mathrm {bad,b}}$
on
![]() $\mathfrak {D}_{k,0}^{o,(u)} /\mathfrak {Fil}_b^{(u)}$
. Here,
$\mathfrak {D}_{k,0}^{o,(u)} /\mathfrak {Fil}_b^{(u)}$
. Here,
![]() $\gamma :\mathcal {X}_0^{(u)}\subset \mathcal {X}_0^{(u-1)}$
is the inclusion.
$\gamma :\mathcal {X}_0^{(u)}\subset \mathcal {X}_0^{(u-1)}$
is the inclusion.
Proof. We use the notation of Proposition 4.16. It suffices to prove both statements after passing to a log affinoid perfectoid cover U of
![]() $\mathcal {X}_{0,\lambda }^{(u)}$
for
$\mathcal {X}_{0,\lambda }^{(u)}$
for
![]() $\lambda =\lambda _0+\lambda _1p+\ldots +\lambda _{n-1}p^{n-1}$
,
$\lambda =\lambda _0+\lambda _1p+\ldots +\lambda _{n-1}p^{n-1}$
,
![]() $\lambda _i\in \{0,1,\ldots ,p-1\}$
, for
$\lambda _i\in \{0,1,\ldots ,p-1\}$
, for
![]() $i=0,1,\ldots ,n-1$
, with associated affinoid perfectoid space
$i=0,1,\ldots ,n-1$
, with associated affinoid perfectoid space
![]() $\widehat {U}:=\mathrm {Spa}(R,R^+)$
. Recall from loc. cit. that
$\widehat {U}:=\mathrm {Spa}(R,R^+)$
. Recall from loc. cit. that
![]() $T_p(E)$
is trivialized
$T_p(E)$
is trivialized
![]() $T_p(E)(U)={\mathbb Z}_p\alpha \oplus {\mathbb Z}_p \beta $
, where the level subgroup is generated by
$T_p(E)(U)={\mathbb Z}_p\alpha \oplus {\mathbb Z}_p \beta $
, where the level subgroup is generated by
![]() $\alpha $
and the canonical subgroup is generated by the section
$\alpha $
and the canonical subgroup is generated by the section
![]() $\beta +\lambda \alpha $
. For every
$\beta +\lambda \alpha $
. For every
![]() $\lambda $
as above, write
$\lambda $
as above, write
![]() $\lambda =\lambda _0 + p \lambda '$
, and then
$\lambda =\lambda _0 + p \lambda '$
, and then
![]() $U_p^{\mathrm {bad}}$
restricts to a map
$U_p^{\mathrm {bad}}$
restricts to a map
![]() $u_{\lambda _0}\colon \mathcal {X}_0(p^n,N)_{0,\lambda }^{(m)} \to \mathcal {X}_0(p^n,N)_{0,\lambda '}^{(m-1)}$
. At the level of universal elliptic curves over U, it corresponds to the p-isogeny defined by
$u_{\lambda _0}\colon \mathcal {X}_0(p^n,N)_{0,\lambda }^{(m)} \to \mathcal {X}_0(p^n,N)_{0,\lambda '}^{(m-1)}$
. At the level of universal elliptic curves over U, it corresponds to the p-isogeny defined by
![]() $u_{\lambda _0}\colon T_p(E)(U)\to T_p(E')(U)$
with
$u_{\lambda _0}\colon T_p(E)(U)\to T_p(E')(U)$
with
![]() $T_p(E')(U)={\mathbb Z}_p \alpha \oplus {\mathbb Z}_p \beta '$
with
$T_p(E')(U)={\mathbb Z}_p \alpha \oplus {\mathbb Z}_p \beta '$
with
![]() $\beta '=\frac {\beta +\lambda _0 \alpha }{p}$
in
$\beta '=\frac {\beta +\lambda _0 \alpha }{p}$
in
![]() $T_p(E)\otimes {\mathbb Q}$
. Notice that
$T_p(E)\otimes {\mathbb Q}$
. Notice that
![]() $\frac {\beta +\lambda \alpha }{p}= \beta ' + \lambda ' \alpha $
defines a generator of the canonical subgroup on
$\frac {\beta +\lambda \alpha }{p}= \beta ' + \lambda ' \alpha $
defines a generator of the canonical subgroup on
![]() $E'$
. The map
$E'$
. The map
![]() $u_{\lambda _0}$
induces by functoriality the map
$u_{\lambda _0}$
induces by functoriality the map
![]() $\mathfrak {D}_{k,0,\lambda }^{o,(u)} \to u^{\ast } \bigl (\mathfrak {D}_{k,0,\lambda _0}^{o,(u-1)} \bigr )$
. We describe it explicitly.
$\mathfrak {D}_{k,0,\lambda }^{o,(u)} \to u^{\ast } \bigl (\mathfrak {D}_{k,0,\lambda _0}^{o,(u-1)} \bigr )$
. We describe it explicitly.
Write
![]() $T_p(E)(U)\otimes R^+=R^+ f_0 \oplus R^+ f_1$
as in Proposition 4.16 so that
$T_p(E)(U)\otimes R^+=R^+ f_0 \oplus R^+ f_1$
as in Proposition 4.16 so that
![]() $f_0\equiv \beta +\lambda \alpha $
and
$f_0\equiv \beta +\lambda \alpha $
and
![]() $f_1\equiv a$
modulo
$f_1\equiv a$
modulo
![]() $p^n$
and
$p^n$
and
![]() $T_p(E)^{\vee }(U)\otimes R^+=e_0 R^+\oplus e_1R^+$
with
$T_p(E)^{\vee }(U)\otimes R^+=e_0 R^+\oplus e_1R^+$
with
![]() $e_0=f_0^{\vee }\equiv \beta ^{\vee }$
mapping to a generator of
$e_0=f_0^{\vee }\equiv \beta ^{\vee }$
mapping to a generator of
![]() $\omega _E^{\mathrm { mod}}$
and
$\omega _E^{\mathrm { mod}}$
and
![]() $e_1=f_1^{\vee }\equiv \alpha ^{\vee }-\lambda \beta ^{\vee }$
in the kernel of
$e_1=f_1^{\vee }\equiv \alpha ^{\vee }-\lambda \beta ^{\vee }$
in the kernel of
![]() $\mathrm {dlog}$
generating
$\mathrm {dlog}$
generating
![]() $\omega _E^{\mathrm {mod,-1}}$
. Then
$\omega _E^{\mathrm {mod,-1}}$
. Then
![]() $\mathfrak {W}_{k,0,\lambda }^{(u),\vee }(U)$
is the dual of
$\mathfrak {W}_{k,0,\lambda }^{(u),\vee }(U)$
is the dual of
![]() $\mathfrak {W}_{k,0,\lambda }^{(u)}(U)\cong R^+\otimes B\langle \frac {W_{\lambda }}{1+p^r Z} \rangle \cdot k(1+p^r Z)$
. Similarly, write
$\mathfrak {W}_{k,0,\lambda }^{(u)}(U)\cong R^+\otimes B\langle \frac {W_{\lambda }}{1+p^r Z} \rangle \cdot k(1+p^r Z)$
. Similarly, write
![]() $T_p(E')(U)\otimes R^+=R^+ f_0' \oplus R^+ f_1'$
with
$T_p(E')(U)\otimes R^+=R^+ f_0' \oplus R^+ f_1'$
with
![]() $f_0'=\frac {f_0}{p}=\beta ' + \lambda ' \alpha $
and
$f_0'=\frac {f_0}{p}=\beta ' + \lambda ' \alpha $
and
![]() $f_1'=f_1$
. Then
$f_1'=f_1$
. Then
![]() $T_p(E')^{\vee }(U)\otimes R^+=e_0' R^+\oplus e_1'R^+$
with
$T_p(E')^{\vee }(U)\otimes R^+=e_0' R^+\oplus e_1'R^+$
with
![]() $e_0'=(f_0')^{\vee }=p e_0$
mapping to a generator of
$e_0'=(f_0')^{\vee }=p e_0$
mapping to a generator of
![]() $\omega _{E'}^{\mathrm {mod}}$
and
$\omega _{E'}^{\mathrm {mod}}$
and
![]() $e_1'=(f_1')^{\vee }=f_1$
in the kernel of
$e_1'=(f_1')^{\vee }=f_1$
in the kernel of
![]() $\mathrm { dlog}$
for
$\mathrm { dlog}$
for
![]() $E'$
generating
$E'$
generating
![]() $\omega _{E'}^{\mathrm {mod,-1}}$
. In particular,
$\omega _{E'}^{\mathrm {mod,-1}}$
. In particular,
![]() $\mathfrak {W}_{k,0,\lambda _0}^{(u-1),\vee }(U)$
is the dual of
$\mathfrak {W}_{k,0,\lambda _0}^{(u-1),\vee }(U)$
is the dual of
![]() $\mathfrak {W}_{k,0,\lambda _0}^{(u-1)}(U)\cong R^+\otimes B\langle \frac {W_{\lambda _0}'}{1+p^r Z'} \rangle \cdot k(1+p^r Z')$
. The map
$\mathfrak {W}_{k,0,\lambda _0}^{(u-1)}(U)\cong R^+\otimes B\langle \frac {W_{\lambda _0}'}{1+p^r Z'} \rangle \cdot k(1+p^r Z')$
. The map
![]() $T_p(E)\to T_p(E')$
induces a map
$T_p(E)\to T_p(E')$
induces a map
![]() $T_p(E')^{\vee } \to T_p(E)^{\vee }$
on the duals and, hence, a map
$T_p(E')^{\vee } \to T_p(E)^{\vee }$
on the duals and, hence, a map
As the decreasing filtrations are defined by
 $$ \begin{align*} \mathrm{Fil}^b \mathfrak{W}_{k,0,\lambda}^{(u)}(U)= \mathfrak{W}_{k,0,\lambda}^{(u)}(U) \cdot \bigl( \frac{W_{\lambda}}{1+p^r Z} \bigr)^b,\quad \mathrm{Fil}^b \mathfrak{W}_{k,0,\lambda_0}^{(u-1)}(U)= \mathfrak{W}_{k,0,\lambda_0}^{(u-1)}(U) \cdot \bigl(\frac{W_{\lambda_0}'}{1+p^r Z'} \bigr)^b, \end{align*} $$
$$ \begin{align*} \mathrm{Fil}^b \mathfrak{W}_{k,0,\lambda}^{(u)}(U)= \mathfrak{W}_{k,0,\lambda}^{(u)}(U) \cdot \bigl( \frac{W_{\lambda}}{1+p^r Z} \bigr)^b,\quad \mathrm{Fil}^b \mathfrak{W}_{k,0,\lambda_0}^{(u-1)}(U)= \mathfrak{W}_{k,0,\lambda_0}^{(u-1)}(U) \cdot \bigl(\frac{W_{\lambda_0}'}{1+p^r Z'} \bigr)^b, \end{align*} $$
we see that
![]() $v_{\lambda }$
respects the filtrations and on
$v_{\lambda }$
respects the filtrations and on
![]() $\mathrm {Fil}^b$
can be written as
$\mathrm {Fil}^b$
can be written as
![]() $p^b v_{\lambda }'$
with
$p^b v_{\lambda }'$
with
![]() $v_{\lambda }'\colon \mathrm { Fil}^b \mathfrak {W}_{k,0,\lambda }^{(u)}(U)\to \mathrm {Fil}^b \mathfrak {W}_{k,0,\lambda _0}^{(u-1)}(U)$
. The claim follows upon taking strong
$v_{\lambda }'\colon \mathrm { Fil}^b \mathfrak {W}_{k,0,\lambda }^{(u)}(U)\to \mathrm {Fil}^b \mathfrak {W}_{k,0,\lambda _0}^{(u-1)}(U)$
. The claim follows upon taking strong
![]() $R^+$
-duals.
$R^+$
-duals.
iii) Given
![]() $h\in {\mathbb N}$
, there exists an integer d such that
$h\in {\mathbb N}$
, there exists an integer d such that
![]() $p^d$
annihilates
$p^d$
annihilates
![]() $\mathrm {Ker}\Bigl (\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(m)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr ) \longrightarrow \mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(m)})_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )\Bigr )$
and
$\mathrm {Ker}\Bigl (\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(m)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr ) \longrightarrow \mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(m)})_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )\Bigr )$
and
![]() $p^de_h$
is integral, where
$p^de_h$
is integral, where
![]() $e_h$
is an idempotent projecting onto the slope
$e_h$
is an idempotent projecting onto the slope
![]() $\le h$
parts of
$\le h$
parts of
![]() $\mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )$
and of
$\mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )$
and of
![]() $\mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(m)})_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )$
. This is the main result of §7.
$\mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(m)})_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )$
. This is the main result of §7.
Proof of Theorem 5.2
We now start the proof of Theorem 5.2. We work with a weight k as in Definition 3.6, which will be assumed in this proof to be the universal weight of some (wide) open disk of the weight space. The case of a finite extension of
![]() ${\mathbb Q}_p$
is obtained by specialization. In particular,
${\mathbb Q}_p$
is obtained by specialization. In particular,
![]() $u_k-i $
is not
$u_k-i $
is not
![]() $0$
in B for every
$0$
in B for every
![]() $i\in {\mathbb N}$
. This will be used in step 3.
$i\in {\mathbb N}$
. This will be used in step 3.
We recall that we have fixed a slope
![]() $h\in {\mathbb N}$
and consider the module
$h\in {\mathbb N}$
and consider the module
Let
![]() $Q(T)\in (B\widehat {\otimes }{\cal O}_{{\mathbb C}_p})[T]$
be the polynomial with
$Q(T)\in (B\widehat {\otimes }{\cal O}_{{\mathbb C}_p})[T]$
be the polynomial with
![]() $\mathrm {deg}(Q(T))\ge 1$
and having the property:
$\mathrm {deg}(Q(T))\ge 1$
and having the property:
![]() $y\in \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )^{(h)}$
if and only if
$y\in \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )^{(h)}$
if and only if
![]() $Q(U_p)y=0$
. Such a polynomial exists as by [Reference Andreatta, Iovita and Stevens6] we have an isomorphism
$Q(U_p)y=0$
. Such a polynomial exists as by [Reference Andreatta, Iovita and Stevens6] we have an isomorphism
![]() $\mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )^{(h)}\cong \mathrm {H}^0\bigl (\mathcal {X}_{\infty }^{(u)}, \omega ^{k+2}_E\bigr )^{(h)}$
and on
$\mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k\bigr )^{(h)}\cong \mathrm {H}^0\bigl (\mathcal {X}_{\infty }^{(u)}, \omega ^{k+2}_E\bigr )^{(h)}$
and on
![]() $\mathrm {H}^0\bigl (\mathcal {X}_{\infty }^{(u)}, \omega ^{k+2}_E\bigr )$
the operator
$\mathrm {H}^0\bigl (\mathcal {X}_{\infty }^{(u)}, \omega ^{k+2}_E\bigr )$
the operator
![]() $U_p$
is compact and has a Fredholm determinant which is an entire power series.
$U_p$
is compact and has a Fredholm determinant which is an entire power series.
![]() $Q(T)$
is obtained from a factor of this Fredholm determinant. We write
$Q(T)$
is obtained from a factor of this Fredholm determinant. We write
![]() $Q(T)=P(T)-\alpha $
, with
$Q(T)=P(T)-\alpha $
, with
![]() $P(T)=TR(T)$
and remark that there is nonnegative
$P(T)=TR(T)$
and remark that there is nonnegative
![]() $a\in {\mathbb Q}$
such that
$a\in {\mathbb Q}$
such that
![]() $\alpha \in p^a(B\widehat {\otimes }{\cal O}_{{\mathbb C}_p})^{\ast }$
. Then
$\alpha \in p^a(B\widehat {\otimes }{\cal O}_{{\mathbb C}_p})^{\ast }$
. Then
![]() $a\le h \cdot \mathrm {deg}(Q(T))$
. Now, we choose integers b with
$a\le h \cdot \mathrm {deg}(Q(T))$
. Now, we choose integers b with
![]() $b\geq 2a+2$
,
$b\geq 2a+2$
,
![]() $s:=(r+c)b+q$
(see i) above) and d as in iii) above. Then it is easy to verify that there exist integers m and
$s:=(r+c)b+q$
(see i) above) and d as in iii) above. Then it is easy to verify that there exist integers m and
![]() $\theta \ge 1$
such that
$\theta \ge 1$
such that
We will work with the open affinoids
![]() $\mathcal {X}_{\infty }^{(u)}:=\mathcal {X}_0(p^n, N)_{\infty }^{(u)}, \ \mathcal {X}_0^{(m)}:=\mathcal {X}_0(p^n, N)_0^{(m)}, \mathcal {X}_0^{m+1)}:=\mathcal {X}_0(p^n, N)_0^{(m+1)}\subset \mathcal {X}_0(p^n, N)$
and their pro-Kummer étale sites.
$\mathcal {X}_{\infty }^{(u)}:=\mathcal {X}_0(p^n, N)_{\infty }^{(u)}, \ \mathcal {X}_0^{(m)}:=\mathcal {X}_0(p^n, N)_0^{(m)}, \mathcal {X}_0^{m+1)}:=\mathcal {X}_0(p^n, N)_0^{(m+1)}\subset \mathcal {X}_0(p^n, N)$
and their pro-Kummer étale sites.
Step 1. Fix
![]() $x\in \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k \bigr )^{(h)}$
, then
$x\in \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k \bigr )^{(h)}$
, then
![]() $P(U_p)x=\alpha x$
. Without loss of generality, we may consider
$P(U_p)x=\alpha x$
. Without loss of generality, we may consider
![]() $x\in \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}^o_k \bigr )^{\mathrm { tf}}$
such that
$x\in \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}^o_k \bigr )^{\mathrm { tf}}$
such that
![]() $P(U_p)x=\alpha x$
(this notation was introduced in Section §7) as
$P(U_p)x=\alpha x$
(this notation was introduced in Section §7) as
![]() $\mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k \bigr )=\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}^o_k \bigr )[1/p]$
. Then there is a unique
$\mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k \bigr )=\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}^o_k \bigr )[1/p]$
. Then there is a unique
![]() $x'\in \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}^o_k \bigr )$
with
$x'\in \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}^o_k \bigr )$
with
![]() $P(U_p)x'=\alpha x'$
and
$P(U_p)x'=\alpha x'$
and
![]() $(x')^{\mathrm {tf}}=p^dx$
, and using Corollary 5.5 ii), we have:
$(x')^{\mathrm {tf}}=p^dx$
, and using Corollary 5.5 ii), we have:
![]() $P(U_p)^{u}(x')\in \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(1)})_{\mathrm {pke}}, {\mathfrak {D}}^o_k \bigr )$
, and by using Corollary 5.5 i), we have that
$P(U_p)^{u}(x')\in \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(1)})_{\mathrm {pke}}, {\mathfrak {D}}^o_k \bigr )$
, and by using Corollary 5.5 i), we have that
![]() $P(U_p)^{m+u+1}(x')\in \mathrm { H}^1\bigl ((\mathcal {X}\backslash \mathcal {X}_0^{(m+1})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr ).$
Denote
$P(U_p)^{m+u+1}(x')\in \mathrm { H}^1\bigl ((\mathcal {X}\backslash \mathcal {X}_0^{(m+1})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr ).$
Denote
![]() $\tilde {x}$
the image of
$\tilde {x}$
the image of
![]() $P(U_p)^{m+u+1}(x')$
in
$P(U_p)^{m+u+1}(x')$
in
![]() $\mathrm {H}^1\bigl ((\mathcal {X}\backslash \mathcal {X}_0^{(m+1)})_{\mathrm {pke}}, {\mathfrak {D}}^o_k/p^{\theta }{\mathfrak {D}}_k^o \bigr )$
.
$\mathrm {H}^1\bigl ((\mathcal {X}\backslash \mathcal {X}_0^{(m+1)})_{\mathrm {pke}}, {\mathfrak {D}}^o_k/p^{\theta }{\mathfrak {D}}_k^o \bigr )$
.
We recall that
![]() $P(U_p)^{u+1}(x')=P(U_p)\bigl (P(U_p)^u(x') \bigr )\in \mathrm {H}^1((\mathcal {X}_{\infty }\backslash \mathcal {X}_0^{(1)} )_{\mathrm {prok}}, {\mathfrak {D}}_k^o)$
by Corollary 5.5 i) and so denote
$P(U_p)^{u+1}(x')=P(U_p)\bigl (P(U_p)^u(x') \bigr )\in \mathrm {H}^1((\mathcal {X}_{\infty }\backslash \mathcal {X}_0^{(1)} )_{\mathrm {prok}}, {\mathfrak {D}}_k^o)$
by Corollary 5.5 i) and so denote
![]() $\mathcal {P}\bigl (x\bigr )$
the image of
$\mathcal {P}\bigl (x\bigr )$
the image of
in
![]() $\mathrm {H}^1\bigl ((\mathcal {X}_0^{(m)})_{\mathrm {pke}}, {\mathfrak {D}}^o_k/p^{\theta }{\mathfrak {D}}_k^o \bigr )$
.
$\mathrm {H}^1\bigl ((\mathcal {X}_0^{(m)})_{\mathrm {pke}}, {\mathfrak {D}}^o_k/p^{\theta }{\mathfrak {D}}_k^o \bigr )$
.
Now, let us observe that the opens
![]() $(\mathcal {X}\backslash \mathcal {X}_0^{(m+1)})$
and
$(\mathcal {X}\backslash \mathcal {X}_0^{(m+1)})$
and
![]() $\mathcal {X}_0^{(m)}$
constitute an open covering of
$\mathcal {X}_0^{(m)}$
constitute an open covering of
![]() $\mathcal {X}$
, and so we have a Mayer–Vietoris exact sequence:
$\mathcal {X}$
, and so we have a Mayer–Vietoris exact sequence:
together with an almost isomorphism
![]() $\displaystyle \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )\widehat {\otimes } {\cal O}_{{\mathbb C}_p}\stackrel {\rho }{\longrightarrow } \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathfrak {D}}^o_k\bigr )$
. We consider the element
$\displaystyle \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )\widehat {\otimes } {\cal O}_{{\mathbb C}_p}\stackrel {\rho }{\longrightarrow } \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathfrak {D}}^o_k\bigr )$
. We consider the element
and we first claim that
![]() $\psi (A,B)=0$
.
$\psi (A,B)=0$
.
Indeed, let us denote by
![]() $\mathcal {V}$
the pro-Kummer étale site
$\mathcal {V}$
the pro-Kummer étale site
![]() $(\mathcal {X}_0^{(m)}\backslash \mathcal {X}_0^{(m+1)})_{\mathrm {pke}}$
. Thanks to Corollary 5.5 iv), we have
$(\mathcal {X}_0^{(m)}\backslash \mathcal {X}_0^{(m+1)})_{\mathrm {pke}}$
. Thanks to Corollary 5.5 iv), we have
Now, let us recall that we have an exact sequence
Using Proposition 5.6 and the fact that
![]() $mb\ge \theta $
, we have
$mb\ge \theta $
, we have
![]() $g\big ((P(U_p)^{m})^{\mathrm {bad}}\bigl (P(U_p)^{u+1}(x') \bigr )=0$
which implies that there is
$g\big ((P(U_p)^{m})^{\mathrm {bad}}\bigl (P(U_p)^{u+1}(x') \bigr )=0$
which implies that there is
![]() $\beta \in \mathrm {H}^1\bigl ({\cal V}, {\mathfrak {Fil}}_b/p^{\theta }{\mathfrak {Fil}}_h\bigr )$
such that
$\beta \in \mathrm {H}^1\bigl ({\cal V}, {\mathfrak {Fil}}_b/p^{\theta }{\mathfrak {Fil}}_h\bigr )$
such that
![]() $\bigl (P(U_p)^{m}\bigr )^{\mathrm {bad}}\bigl (P(U_p)^{u+1}(x') \bigr ) =f(\beta )$
. But by i) above, the image of f is annihilated by
$\bigl (P(U_p)^{m}\bigr )^{\mathrm {bad}}\bigl (P(U_p)^{u+1}(x') \bigr ) =f(\beta )$
. But by i) above, the image of f is annihilated by
![]() $p^s$
, therefore
$p^s$
, therefore
![]() $\psi (A,B)=p^sf(\beta )=0$
. This proves the claim.
$\psi (A,B)=p^sf(\beta )=0$
. This proves the claim.
We continue the proof of the theorem. The Mayer–Vietoris exact sequence implies that there is
![]() $y\in \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )\widehat {\otimes } {\cal O}_{{\mathbb C}_p}$
such that
$y\in \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )\widehat {\otimes } {\cal O}_{{\mathbb C}_p}$
such that
Let
![]() $z_0\in \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )\widehat {\otimes } {\cal O}_{{\mathbb C}_p}$
be
$z_0\in \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )\widehat {\otimes } {\cal O}_{{\mathbb C}_p}$
be
![]() $z_0:=p^de_h(y)$
. Then
$z_0:=p^de_h(y)$
. Then
![]() $z_0\in \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )^{(h)}\widehat {\otimes } {\cal O}_{{\mathbb C}_p}$
and
$z_0\in \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )^{(h)}\widehat {\otimes } {\cal O}_{{\mathbb C}_p}$
and
![]() $\rho (z_0)|_{(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}}\equiv p^{s+d+1}\alpha ^{m+u+1}x'\ \Bigl (\mathrm {mod}\ p^{\theta }\mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}} , {\mathfrak {D}}_k^o \bigr )^{(b)}\Bigr )$
, where we write
$\rho (z_0)|_{(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}}\equiv p^{s+d+1}\alpha ^{m+u+1}x'\ \Bigl (\mathrm {mod}\ p^{\theta }\mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}} , {\mathfrak {D}}_k^o \bigr )^{(b)}\Bigr )$
, where we write
![]() $\mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}} , {\mathfrak {D}}_k^o \bigr )^{(h)}$
for the image
$\mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}} , {\mathfrak {D}}_k^o \bigr )^{(h)}$
for the image
![]() $p^d e_h \mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}} , {\mathfrak {D}}_k^o \bigr )$
.
$p^d e_h \mathrm { H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}} , {\mathfrak {D}}_k^o \bigr )$
.
Step 2. Let
![]() $x_1\in \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )^{(h)}$
be such that
$x_1\in \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )^{(h)}$
be such that
![]() $\rho (z_0)|_{(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}}=p^{s+d+1}\alpha ^{m+u+1}\bigl (x'-p^{\theta /2} x_1 \bigr )$
. Such
$\rho (z_0)|_{(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}}=p^{s+d+1}\alpha ^{m+u+1}\bigl (x'-p^{\theta /2} x_1 \bigr )$
. Such
![]() $x_1$
exists indeed because
$x_1$
exists indeed because
![]() $x_1\in p^{-s-d-1+\theta /2}\alpha ^{-m-u-1}\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )^{(h)}\subset \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )^{(h)}$
.
$x_1\in p^{-s-d-1+\theta /2}\alpha ^{-m-u-1}\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )^{(h)}\subset \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )^{(h)}$
.
Now, we apply to
![]() $x_1$
the Step 1 we used on x and obtain
$x_1$
the Step 1 we used on x and obtain
![]() $z_1\in \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )^{(h)}\widehat {\otimes } {\cal O}_{{\mathbb C}_p}$
such that
$z_1\in \mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )^{(h)}\widehat {\otimes } {\cal O}_{{\mathbb C}_p}$
such that
![]() $\rho (z_1)\equiv p^{s+d+1}\alpha ^{m+u+1}x_1 \Bigl (\mathrm {mod}\ p^{\theta } \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )^{(b)}\Bigr )$
.
$\rho (z_1)\equiv p^{s+d+1}\alpha ^{m+u+1}x_1 \Bigl (\mathrm {mod}\ p^{\theta } \mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )^{(b)}\Bigr )$
.
We remark that
![]() $\rho (z_0+p^{\theta /2}z_1)|_{(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}}\equiv p^{s+d+1}\alpha ^{m+u+1}x' \ \Bigl (\mathrm {mod}\ p^{3\theta /2}\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )^{(b)}\Bigr )$
.
$\rho (z_0+p^{\theta /2}z_1)|_{(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}}\equiv p^{s+d+1}\alpha ^{m+u+1}x' \ \Bigl (\mathrm {mod}\ p^{3\theta /2}\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o \bigr )^{(b)}\Bigr )$
.
Repeating Step 2, we construct inductively a sequence
![]() $(z_v)_{v\ge 0}$
in
$(z_v)_{v\ge 0}$
in
![]() $\mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )^{(h)}\widehat {\otimes } {\cal O}_{{\mathbb C}_p}$
such that for every
$\mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )^{(h)}\widehat {\otimes } {\cal O}_{{\mathbb C}_p}$
such that for every
![]() $v\ge 0$
we have
$v\ge 0$
we have
 $$ \begin{align*} \rho\bigl(\sum_{j=0}^vp^{j\theta/2}z_j \bigr)|_{(\mathcal{X}_{\infty}^{(u)})_{\mathrm{pke}}}\equiv p^{s+d+1}\alpha^{m+u+1}x' \ \Bigl(\mathrm{mod}\ p^{(2v+1)\theta/2}\mathrm{H}^1\bigl((\mathcal{X}_{\infty}^{(u)})_{\mathrm{pke}}, {\mathfrak{D}}_k^o \bigr)^{(b)}\Bigr). \end{align*} $$
$$ \begin{align*} \rho\bigl(\sum_{j=0}^vp^{j\theta/2}z_j \bigr)|_{(\mathcal{X}_{\infty}^{(u)})_{\mathrm{pke}}}\equiv p^{s+d+1}\alpha^{m+u+1}x' \ \Bigl(\mathrm{mod}\ p^{(2v+1)\theta/2}\mathrm{H}^1\bigl((\mathcal{X}_{\infty}^{(u)})_{\mathrm{pke}}, {\mathfrak{D}}_k^o \bigr)^{(b)}\Bigr). \end{align*} $$
If we denote by
 $$ \begin{align*} z:=p^{-s-d-1}\alpha^{-m-u-1}\sum_{j=0}^{\infty} p^{j\theta/2}z_j\in \mathrm{H}^1\bigl(\mathcal{X}_{\mathrm{pke}}, {\mathbb D}^o_k\bigr)^{(h)}\widehat{\otimes} {\mathbb C}_p, \end{align*} $$
$$ \begin{align*} z:=p^{-s-d-1}\alpha^{-m-u-1}\sum_{j=0}^{\infty} p^{j\theta/2}z_j\in \mathrm{H}^1\bigl(\mathcal{X}_{\mathrm{pke}}, {\mathbb D}^o_k\bigr)^{(h)}\widehat{\otimes} {\mathbb C}_p, \end{align*} $$
then
![]() $\rho \bigl (p^{-d}z\bigr )|_{(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}}=p^{-d}\bigl ((x')^{\mathrm {tf}}\bigr )=x$
. To see that the written series converges, we recall (see [Reference Andreatta, Iovita and Stevens5]) that
$\rho \bigl (p^{-d}z\bigr )|_{(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}}=p^{-d}\bigl ((x')^{\mathrm {tf}}\bigr )=x$
. To see that the written series converges, we recall (see [Reference Andreatta, Iovita and Stevens5]) that
![]() $\mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )$
is profinite, therefore compact, and so
$\mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )$
is profinite, therefore compact, and so
![]() $\mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )^{(h)}\widehat {\otimes } {\mathbb C}_p$
is complete for the p-adic topology.
$\mathrm {H}^1\bigl (\mathcal {X}_{\mathrm {pke}}, {\mathbb D}^o_k\bigr )^{(h)}\widehat {\otimes } {\mathbb C}_p$
is complete for the p-adic topology.
Step 3. Using step (2), Theorem 5.2 is proven under the condition that
![]() $\Bigl (\prod _{i=0}^{b-1} (u_k-i)\Bigr )\in B[1/p]^{\ast }$
. As no
$\Bigl (\prod _{i=0}^{b-1} (u_k-i)\Bigr )\in B[1/p]^{\ast }$
. As no
![]() $u_k-i$
is
$u_k-i$
is
![]() $0$
in B due to our assumptions, we have
$0$
in B due to our assumptions, we have
![]() $B\bigl [p^{-1}\prod _{i=h}^{h-1} (u_k-i)^{-1} \bigr ]=\cap _{n\in {\mathbb N}} B_n[p^{-1}]$
, with
$B\bigl [p^{-1}\prod _{i=h}^{h-1} (u_k-i)^{-1} \bigr ]=\cap _{n\in {\mathbb N}} B_n[p^{-1}]$
, with
![]() $B_n=B\big [\!\big [p^n/\prod _{i=h}^{b-1}(u_k-i) \big ]\!\big ]$
satisfying the requirements of Definition 3.6 for every
$B_n=B\big [\!\big [p^n/\prod _{i=h}^{b-1}(u_k-i) \big ]\!\big ]$
satisfying the requirements of Definition 3.6 for every
![]() $n\ge 0$
. The theorem then holds for each
$n\ge 0$
. The theorem then holds for each
![]() $B_n$
. Since the map
$B_n$
. Since the map
![]() $\mathcal {R}$
is a map of finite and projective
$\mathcal {R}$
is a map of finite and projective
![]() $B[1/p]$
-modules, we get that Theorem 5.2 holds after inverting
$B[1/p]$
-modules, we get that Theorem 5.2 holds after inverting
![]() $\prod _{i=h}^{b-1}(u_k-i)$
.
$\prod _{i=h}^{b-1}(u_k-i)$
.
Consider the reduction of
![]() $\Psi _{\mathrm {HT}}$
modulo
$\Psi _{\mathrm {HT}}$
modulo
![]() $u_k-i$
, for
$u_k-i$
, for
![]() $h\leq i\leq b-1$
. It is compatible with the classical p-adic Hodge–Tate decomposition, which provides a surjective map
$h\leq i\leq b-1$
. It is compatible with the classical p-adic Hodge–Tate decomposition, which provides a surjective map
see [Reference Andreatta, Iovita and Stevens5]. The map
![]() $\mathrm {H}^1\bigl (\mathcal {X}_{\overline {K},{\mathrm {pke}}}, {\mathbb D}_i^o(T_0^{\vee })[n]\bigr )\to \mathrm {H}^1\bigl (\mathcal {X}_{\overline {K},{\mathrm {pke}}}, \mathrm {Sym}^{i}(T_0^{\vee })\bigr )$
is induced by the surjective map
$\mathrm {H}^1\bigl (\mathcal {X}_{\overline {K},{\mathrm {pke}}}, {\mathbb D}_i^o(T_0^{\vee })[n]\bigr )\to \mathrm {H}^1\bigl (\mathcal {X}_{\overline {K},{\mathrm {pke}}}, \mathrm {Sym}^{i}(T_0^{\vee })\bigr )$
is induced by the surjective map
![]() ${\mathbb D}_k^o(T_0^{\vee })[n]/(u_k-i)\cong {\mathbb D}_i^o(T_0^{\vee })[n] \to \mathrm {Sym}^{i}(T_0^{\vee })$
and induces a surjective morphism on the slope
${\mathbb D}_k^o(T_0^{\vee })[n]/(u_k-i)\cong {\mathbb D}_i^o(T_0^{\vee })[n] \to \mathrm {Sym}^{i}(T_0^{\vee })$
and induces a surjective morphism on the slope
![]() $\leq h$
-part
$\leq h$
-part
![]() $\mathrm {H}^1\bigl (\mathcal {X}_{\overline {K},{\mathrm {pke}}}, {\_}\bigr )^{(h)}$
, by results of Stevens. The map
$\mathrm {H}^1\bigl (\mathcal {X}_{\overline {K},{\mathrm {pke}}}, {\_}\bigr )^{(h)}$
, by results of Stevens. The map
![]() $\mathrm {H}^0\bigl (\mathcal {X}, \omega ^{i+2}_E\bigr )\to \mathrm {H}^0\bigl (\mathcal {X}_{\infty }^{(u)}, \omega ^{i+2}_E\bigr )\cong \mathrm {H}^0\bigl (\mathcal {X}_{\infty }^{(u)}, \omega ^{k+2}_E\bigr )/(u_k-i)$
is the restriction map, and it is an isomorphism on the slope
$\mathrm {H}^0\bigl (\mathcal {X}, \omega ^{i+2}_E\bigr )\to \mathrm {H}^0\bigl (\mathcal {X}_{\infty }^{(u)}, \omega ^{i+2}_E\bigr )\cong \mathrm {H}^0\bigl (\mathcal {X}_{\infty }^{(u)}, \omega ^{k+2}_E\bigr )/(u_k-i)$
is the restriction map, and it is an isomorphism on the slope
![]() $\leq h$
-part by the classicity result of Coleman. We conclude that
$\leq h$
-part by the classicity result of Coleman. We conclude that
![]() $\Psi _{\mathrm {HT}}$
, and hence
$\Psi _{\mathrm {HT}}$
, and hence
![]() $\mathcal {R}$
, is surjective modulo
$\mathcal {R}$
, is surjective modulo
![]() $u_k-i$
for every
$u_k-i$
for every
![]() $h\leq i\leq b-1$
. This implies that
$h\leq i\leq b-1$
. This implies that
![]() $\mathcal {R}$
is surjective if
$\mathcal {R}$
is surjective if
![]() $\Bigl (\prod _{i=0}^{h-1}(u_k-i)\Bigr )\in B[1/p]^{\ast }$
, as claimed.
$\Bigl (\prod _{i=0}^{h-1}(u_k-i)\Bigr )\in B[1/p]^{\ast }$
, as claimed.
6 The
 $B_{\mathrm {dR}}$
-comparison
$B_{\mathrm {dR}}$
-comparison
In this section, we consider the modular curve
![]() $\mathcal {X}=\mathcal {X}(N)$
of full-level N and the modular curve
$\mathcal {X}=\mathcal {X}(N)$
of full-level N and the modular curve
![]() $\mathcal {X}_0(p^n,N)$
over the ring of integers
$\mathcal {X}_0(p^n,N)$
over the ring of integers
![]() ${\cal O}_K$
of an unramified extension K of
${\cal O}_K$
of an unramified extension K of
![]() ${\mathbb Q}_p$
. Let
${\mathbb Q}_p$
. Let
![]() $\widehat {X}$
be the p-adic formal scheme over
$\widehat {X}$
be the p-adic formal scheme over
![]() ${\cal O}_K$
defined by formally completing the modular curve
${\cal O}_K$
defined by formally completing the modular curve
![]() $X(N)$
over
$X(N)$
over
![]() ${\cal O}_K$
along the special fibre
${\cal O}_K$
along the special fibre
![]() $X(N)_0$
. Let E be the universal generalised elliptic curve over
$X(N)_0$
. Let E be the universal generalised elliptic curve over
![]() $X(N)$
, and denote its modulo p-reduction by
$X(N)$
, and denote its modulo p-reduction by
![]() $E_0$
. As
$E_0$
. As
![]() $X(N)_0$
is smooth, the crystalline cohomology
$X(N)_0$
is smooth, the crystalline cohomology
![]() $\mathrm {H}^1_{\mathrm {crys}}\bigl (E_0/\widehat {X}\bigr ) $
is identified with the de Rham cohomology
$\mathrm {H}^1_{\mathrm {crys}}\bigl (E_0/\widehat {X}\bigr ) $
is identified with the de Rham cohomology
![]() $\mathrm {H}_E:=\mathrm {H}^1_{\mathrm {dR}}\bigl (E/\widehat {X}\bigr ) $
(as a module with log connection; see its description below).
$\mathrm {H}_E:=\mathrm {H}^1_{\mathrm {dR}}\bigl (E/\widehat {X}\bigr ) $
(as a module with log connection; see its description below).
6.1 Period sheaves
There is a map of sites
![]() $w\colon \mathcal {X}_{{\mathrm {pke}}} \to \widehat {X}_{\mathrm {et}}$
defined by associating to an étale map
$w\colon \mathcal {X}_{{\mathrm {pke}}} \to \widehat {X}_{\mathrm {et}}$
defined by associating to an étale map
![]() $U\to \widehat {X}$
of formal schemes its adic generic fibre. We set
$U\to \widehat {X}$
of formal schemes its adic generic fibre. We set
![]() ${\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^{\mathrm {unr, +}}:=w^{-1}\bigl ({\cal O}_{\widehat {X}}\bigr )$
(see [Reference Tan and Tong25, §2.2]). It is a subsheaf of
${\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^{\mathrm {unr, +}}:=w^{-1}\bigl ({\cal O}_{\widehat {X}}\bigr )$
(see [Reference Tan and Tong25, §2.2]). It is a subsheaf of
![]() ${\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
. As
${\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
. As
![]() $\widehat {X}$
is endowed with the log structure defined by the cusps, this induces a log structure
$\widehat {X}$
is endowed with the log structure defined by the cusps, this induces a log structure
![]() $\widehat {\alpha }\colon \widehat {{\cal M}} \to {\cal O}_{\widehat {X}}$
; more precisely,
$\widehat {\alpha }\colon \widehat {{\cal M}} \to {\cal O}_{\widehat {X}}$
; more precisely,
![]() $ \widehat {{\cal M}}$
is the inverse limit
$ \widehat {{\cal M}}$
is the inverse limit
![]() $\displaystyle {\lim _{\infty \leftarrow n}} {\cal M}_n$
, where
$\displaystyle {\lim _{\infty \leftarrow n}} {\cal M}_n$
, where
![]() ${\cal M}_n\to {\cal O}_{\widehat {X}}/p^n {\cal O}_{\widehat {X}}$
is the log structure defined by the cusps. This induces a log structure
${\cal M}_n\to {\cal O}_{\widehat {X}}/p^n {\cal O}_{\widehat {X}}$
is the log structure defined by the cusps. This induces a log structure
![]() $\alpha ^{\mathrm {unr}}\colon {\cal M}^{\mathrm {unr, +}}:=w^{-1}\bigl ( \widehat {{\cal M}} \bigr ) \to {\cal O}_{\mathcal {X}}^{\mathrm {unr, +}}$
and a log structure
$\alpha ^{\mathrm {unr}}\colon {\cal M}^{\mathrm {unr, +}}:=w^{-1}\bigl ( \widehat {{\cal M}} \bigr ) \to {\cal O}_{\mathcal {X}}^{\mathrm {unr, +}}$
and a log structure
![]() $\alpha ^+\colon {\cal M}^+ \to {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
which defines the log structure
$\alpha ^+\colon {\cal M}^+ \to {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
which defines the log structure
![]() $\alpha \colon {\cal M}\to {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}$
of §2.2. In particular, we can refine the prelog structure
$\alpha \colon {\cal M}\to {\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}$
of §2.2. In particular, we can refine the prelog structure
![]() $\alpha ^{\flat } \colon {\cal M}^{\flat } \to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}^{\flat }}$
of loc. cit. to a prelog structure
$\alpha ^{\flat } \colon {\cal M}^{\flat } \to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}^{\flat }}$
of loc. cit. to a prelog structure
![]() $\alpha ^{\flat ,+} \colon {\cal M}^{\flat ,+} \to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}^{\flat }}^+$
, where
$\alpha ^{\flat ,+} \colon {\cal M}^{\flat ,+} \to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}^{\flat }}^+$
, where
![]() ${\cal M}^{\flat ,+}$
is the inverse limit
${\cal M}^{\flat ,+}$
is the inverse limit
![]() $\displaystyle \lim _{\leftarrow } {\cal M}^+$
, indexed by
$\displaystyle \lim _{\leftarrow } {\cal M}^+$
, indexed by
![]() ${\mathbb N}$
, with transition maps given by raising to the p-th power. We write
${\mathbb N}$
, with transition maps given by raising to the p-th power. We write
![]() $a\mapsto a^{\sharp }$
for the first projection
$a\mapsto a^{\sharp }$
for the first projection
![]() ${\cal M}^{\flat ,+}\to {\cal M}^+$
.
${\cal M}^{\flat ,+}\to {\cal M}^+$
.
Recall that we have the period sheaf
![]() $\mathbb {A}_{\mathrm {inf}}$
over
$\mathbb {A}_{\mathrm {inf}}$
over
![]() $\mathcal {X}_{{\mathrm {pke}}}$
; see §2.2. We define the morphism of multiplicative monoids
$\mathcal {X}_{{\mathrm {pke}}}$
; see §2.2. We define the morphism of multiplicative monoids
![]() $\alpha _{\mathrm {inf}}\colon {\cal M}^{\flat ,+} \to \mathbb {A}_{\mathrm {inf}}$
by composing
$\alpha _{\mathrm {inf}}\colon {\cal M}^{\flat ,+} \to \mathbb {A}_{\mathrm {inf}}$
by composing
![]() $\alpha ^{\flat ,+}$
with the Teichmüller lift. Then the map
$\alpha ^{\flat ,+}$
with the Teichmüller lift. Then the map
![]() $\vartheta \colon \mathbb {A}_{\mathrm {inf}} \to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
is compatible with prelog structures, namely
$\vartheta \colon \mathbb {A}_{\mathrm {inf}} \to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
is compatible with prelog structures, namely
![]() $\vartheta \circ \alpha _{\mathrm {inf}}$
coincides with the first projection
$\vartheta \circ \alpha _{\mathrm {inf}}$
coincides with the first projection
![]() ${\cal M}^{+,\flat } \to {\cal M}^+$
composed with
${\cal M}^{+,\flat } \to {\cal M}^+$
composed with
![]() $\alpha ^+$
and the natural map
$\alpha ^+$
and the natural map
![]() ${\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+ \to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
. The map
${\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^+ \to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
. The map
![]() $\vartheta $
defines a map
$\vartheta $
defines a map
of
![]() ${\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^{\mathrm {unr, +}}$
-algebras. Furthermore,
${\cal O}_{\mathcal {X}_{{\mathrm {pke}}}}^{\mathrm {unr, +}}$
-algebras. Furthermore,
![]() $\vartheta _{\mathcal {X}}$
is a map of sheaves compatible with the prelog structures
$\vartheta _{\mathcal {X}}$
is a map of sheaves compatible with the prelog structures
![]() $\alpha ^{\mathrm {unr}}\times \alpha _{\mathrm {inf}}\colon {\cal M}^{\mathrm {unr, +}} \times {\cal M}^{\flat ,+} \to {\cal O} \mathbb {A}_{\mathrm {inf}}$
and
$\alpha ^{\mathrm {unr}}\times \alpha _{\mathrm {inf}}\colon {\cal M}^{\mathrm {unr, +}} \times {\cal M}^{\flat ,+} \to {\cal O} \mathbb {A}_{\mathrm {inf}}$
and
![]() $\alpha ^+$
; namely,
$\alpha ^+$
; namely,
![]() $\vartheta _{\mathcal {X}} \circ \bigl (\alpha ^{\mathrm {unr}}\times \alpha _{\mathrm {inf}}\bigr ) $
coincides with
$\vartheta _{\mathcal {X}} \circ \bigl (\alpha ^{\mathrm {unr}}\times \alpha _{\mathrm {inf}}\bigr ) $
coincides with
![]() $\alpha ^+$
composed with the homomorphism of monoids
$\alpha ^+$
composed with the homomorphism of monoids
![]() $\tau : {\cal M}^{\mathrm {unr, +}} \times {\cal M}^{\flat , +} \to {\cal M}^+$
provided by the natural map
$\tau : {\cal M}^{\mathrm {unr, +}} \times {\cal M}^{\flat , +} \to {\cal M}^+$
provided by the natural map
![]() ${\cal M}^{\mathrm {unr, +}}\to {\cal M}^{+}$
, the projection
${\cal M}^{\mathrm {unr, +}}\to {\cal M}^{+}$
, the projection
![]() ${\cal M}^{\flat ,+} \to {\cal M}^+ $
given by
${\cal M}^{\flat ,+} \to {\cal M}^+ $
given by
![]() $a\mapsto a^{\sharp }$
and the multiplication map
$a\mapsto a^{\sharp }$
and the multiplication map
![]() ${\cal M}^+\times {\cal M}^+ \to {\cal M}^+$
.
${\cal M}^+\times {\cal M}^+ \to {\cal M}^+$
.
Define
![]() ${\cal O} \mathbb {A}_{\mathrm {log}}$
to be the sheaf on
${\cal O} \mathbb {A}_{\mathrm {log}}$
to be the sheaf on
![]() $\mathcal {X}_{{\mathrm {pke}}}$
given by the p-adic completion of the log-divided powers (DP) envelope of
$\mathcal {X}_{{\mathrm {pke}}}$
given by the p-adic completion of the log-divided powers (DP) envelope of
![]() ${\cal O} \mathbb {A}_{\mathrm {inf}}$
with respect to the product prelog structure
${\cal O} \mathbb {A}_{\mathrm {inf}}$
with respect to the product prelog structure
![]() $\alpha ^{\mathrm {unr}}\times \alpha _{\mathrm {inf}}$
and with respect to
$\alpha ^{\mathrm {unr}}\times \alpha _{\mathrm {inf}}$
and with respect to
![]() $\vartheta _{\mathcal {X}}$
; see [Reference Andreatta and Iovita1, Lemma 2.16] for the definition. More precisely, let
$\vartheta _{\mathcal {X}}$
; see [Reference Andreatta and Iovita1, Lemma 2.16] for the definition. More precisely, let
![]() ${\cal M}' \subset ({\cal M}^{\mathrm {unr, +}})^{\mathrm {gp}} \times ({\cal M}^{\flat ,+})^{\mathrm {gp}} $
be the sheaf of monoids defined as the inverse image of
${\cal M}' \subset ({\cal M}^{\mathrm {unr, +}})^{\mathrm {gp}} \times ({\cal M}^{\flat ,+})^{\mathrm {gp}} $
be the sheaf of monoids defined as the inverse image of
![]() ${\cal M}^+\subset ({\cal M}^+)^{\mathrm {gp}}$
via the map
${\cal M}^+\subset ({\cal M}^+)^{\mathrm {gp}}$
via the map
![]() $\tau ^{\mathrm {gp}}\colon ({\cal M}^{\mathrm {unr, +}})^{\mathrm {gp}} \times ({\cal M}^{\flat ,+})^{\mathrm {gp}}\to ({\cal M}^+)^{\mathrm {gp}}$
associated to
$\tau ^{\mathrm {gp}}\colon ({\cal M}^{\mathrm {unr, +}})^{\mathrm {gp}} \times ({\cal M}^{\flat ,+})^{\mathrm {gp}}\to ({\cal M}^+)^{\mathrm {gp}}$
associated to
![]() $\tau $
defined above; here, the superscript
$\tau $
defined above; here, the superscript
![]() $\mathrm {gp}$
is the sheaf of groups associated to a sheaf of monoids. Let
$\mathrm {gp}$
is the sheaf of groups associated to a sheaf of monoids. Let
![]() ${\cal O} \mathbb {A}_{\mathrm {inf}}':= {\cal O} \mathbb {A}_{\mathrm {inf}}\otimes _{{\mathbb Z}\bigl [{\cal M}^{\mathrm {unr, +}} \times {\cal M}^{\flat ,+}\bigr ]} {\mathbb Z}\bigl [{\cal M}'\bigr ] $
be the log envelope of
${\cal O} \mathbb {A}_{\mathrm {inf}}':= {\cal O} \mathbb {A}_{\mathrm {inf}}\otimes _{{\mathbb Z}\bigl [{\cal M}^{\mathrm {unr, +}} \times {\cal M}^{\flat ,+}\bigr ]} {\mathbb Z}\bigl [{\cal M}'\bigr ] $
be the log envelope of
![]() ${\cal O}_{\mathcal {X}}^{\mathrm {unr +}} \otimes _{{\mathbb Z}_p} \mathbb {A}_{\mathrm {inf}}$
, with respect to prelog structure
${\cal O}_{\mathcal {X}}^{\mathrm {unr +}} \otimes _{{\mathbb Z}_p} \mathbb {A}_{\mathrm {inf}}$
, with respect to prelog structure
![]() ${\cal M}^{\mathrm {unr, +}} \times {\cal M}^{\flat ,+}$
and the map
${\cal M}^{\mathrm {unr, +}} \times {\cal M}^{\flat ,+}$
and the map
![]() $\vartheta _{\mathcal {X}}$
. It is endowed with a tautological prelog structure
$\vartheta _{\mathcal {X}}$
. It is endowed with a tautological prelog structure
![]() $\alpha '\colon {\cal M}'\to {\cal O} \mathbb {A}_{\mathrm {inf}}'$
. The map
$\alpha '\colon {\cal M}'\to {\cal O} \mathbb {A}_{\mathrm {inf}}'$
. The map
![]() $\vartheta _{\mathcal {X}}$
extends uniquely to a map
$\vartheta _{\mathcal {X}}$
extends uniquely to a map
![]() $\vartheta _{\mathcal {X}}'\colon {\cal O} \mathbb {A}_{\mathrm {inf}}' \longrightarrow \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
compatible with the prelog structures
$\vartheta _{\mathcal {X}}'\colon {\cal O} \mathbb {A}_{\mathrm {inf}}' \longrightarrow \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
compatible with the prelog structures
![]() $\alpha '$
and
$\alpha '$
and
![]() $\alpha ^+$
, that is, such that
$\alpha ^+$
, that is, such that
![]() $\vartheta _{\mathcal {X}}' \circ \alpha '$
is
$\vartheta _{\mathcal {X}}' \circ \alpha '$
is
![]() $\alpha ^+$
composed with the natural morphism
$\alpha ^+$
composed with the natural morphism
![]() ${\cal M}'\to {\cal M}^+$
induced by
${\cal M}'\to {\cal M}^+$
induced by
![]() $(\alpha ^{\mathrm {unr}})^{\mathrm {gp}}\times ( \alpha _{\mathrm {inf}})^{\mathrm {gp}}$
. Let
$(\alpha ^{\mathrm {unr}})^{\mathrm {gp}}\times ( \alpha _{\mathrm {inf}})^{\mathrm {gp}}$
. Let
![]() $\mathcal {I}$
be the kernel of
$\mathcal {I}$
be the kernel of
![]() $\vartheta _{\mathcal {X}}'$
.
$\vartheta _{\mathcal {X}}'$
.
Then
![]() ${\cal O}\mathbb {A}_{\mathrm {log}}$
is the p-adic completion of the DP envelope of
${\cal O}\mathbb {A}_{\mathrm {log}}$
is the p-adic completion of the DP envelope of
![]() ${\cal O} \mathbb {A}_{\mathrm {inf}}'$
with respect to the ideal
${\cal O} \mathbb {A}_{\mathrm {inf}}'$
with respect to the ideal
![]() ${\cal I}$
. For every positive integer n, we also define
${\cal I}$
. For every positive integer n, we also define
![]() ${\cal O}\mathbb {A}_{\max ,n}^{\log }$
to be the p-adic completion of the subsheaf
${\cal O}\mathbb {A}_{\max ,n}^{\log }$
to be the p-adic completion of the subsheaf
![]() $\displaystyle {\cal O} \mathbb {A}_{\mathrm {inf}}' \bigl [\frac {\mathcal {I}}{p^n}\bigr ]$
of
$\displaystyle {\cal O} \mathbb {A}_{\mathrm {inf}}' \bigl [\frac {\mathcal {I}}{p^n}\bigr ]$
of
![]() ${\cal O}\mathbb {A}_{\mathrm {inf}}'[p^{-1}]$
. The map
${\cal O}\mathbb {A}_{\mathrm {inf}}'[p^{-1}]$
. The map
![]() $\vartheta _{\mathcal {X}}'$
extends to a map
$\vartheta _{\mathcal {X}}'$
extends to a map
![]() $\vartheta _{\max ,n}\colon {\cal O}\mathbb {A}_{\max ,n}^{\log }\to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
. As
$\vartheta _{\max ,n}\colon {\cal O}\mathbb {A}_{\max ,n}^{\log }\to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
. As
![]() $\mathcal {I}$
admits DP powers in
$\mathcal {I}$
admits DP powers in
![]() ${\cal O} \mathbb {A}_{\max ,n}^{\log }$
and
${\cal O} \mathbb {A}_{\max ,n}^{\log }$
and
![]() ${\cal O}\mathbb {A}_{\log }$
is the p-adic completion of the DP envelope of
${\cal O}\mathbb {A}_{\log }$
is the p-adic completion of the DP envelope of
![]() ${\cal O} \mathbb {A}_{\mathrm {inf}}'$
with respect to
${\cal O} \mathbb {A}_{\mathrm {inf}}'$
with respect to
![]() $\mathcal {I}$
, we have a natural map
$\mathcal {I}$
, we have a natural map
![]() ${\cal O} \mathbb {A}_{\log }\to {\cal O}\mathbb {A}_{\max ,n}^{\log }$
by the universal property of the DP envelope.
${\cal O} \mathbb {A}_{\log }\to {\cal O}\mathbb {A}_{\max ,n}^{\log }$
by the universal property of the DP envelope.
The derivation
![]() $d\colon {\cal O}_{\widehat {X}} \to \Omega ^{\log }_{{\widehat {X}}/{\cal O}_K}$
defines
$d\colon {\cal O}_{\widehat {X}} \to \Omega ^{\log }_{{\widehat {X}}/{\cal O}_K}$
defines
![]() $\mathbb {A}_{\mathrm {inf}}$
-linear connections
$\mathbb {A}_{\mathrm {inf}}$
-linear connections
and
where
![]() $\Omega ^{\mathrm { unr}}_{\mathcal {X}_{{\mathrm {pke}}}}:=w^{-1}\bigl (\Omega ^{\log }_{{\widehat {X}}/{\cal O}_K}\bigr )$
is the inverse image of the logarithmic differentials on
$\Omega ^{\mathrm { unr}}_{\mathcal {X}_{{\mathrm {pke}}}}:=w^{-1}\bigl (\Omega ^{\log }_{{\widehat {X}}/{\cal O}_K}\bigr )$
is the inverse image of the logarithmic differentials on
![]() $\widehat {X}$
.
$\widehat {X}$
.
Remark 6.1. On the complement of the cusps, where the log structure is trivial, the sheaf
![]() ${\cal O} \mathbb {A}_{\mathrm {log}}$
is the p-adic completion of the DP envelope of
${\cal O} \mathbb {A}_{\mathrm {log}}$
is the p-adic completion of the DP envelope of
![]() ${\cal O} \mathbb {A}_{\mathrm {inf}}$
with respect to the kernel of
${\cal O} \mathbb {A}_{\mathrm {inf}}$
with respect to the kernel of
![]() $\vartheta _{\mathcal {X}}$
; it is the sheaf denoted
$\vartheta _{\mathcal {X}}$
; it is the sheaf denoted
![]() ${\cal O} \mathbb {A}_{\mathrm {cris}}$
in [Reference Tan and Tong25, Def. 2.9].
${\cal O} \mathbb {A}_{\mathrm {cris}}$
in [Reference Tan and Tong25, Def. 2.9].
Take an affine open neighbourhood
![]() $\widehat {U}_0\subset \widehat {X}$
of a cusp, with local coordinate Y at the given cusp. Define
$\widehat {U}_0\subset \widehat {X}$
of a cusp, with local coordinate Y at the given cusp. Define
![]() $U_0\subset \mathcal {X}$
to be the associated affinoid with induced log structure. Take
$U_0\subset \mathcal {X}$
to be the associated affinoid with induced log structure. Take
![]() $U=\lim _i U_i$
with
$U=\lim _i U_i$
with
![]() $U_i=\bigl (\mathrm {Spa}(R_i,R_i^+),{\cal M}_i\bigr )$
to be a log affinoid perfectoid with initial object
$U_i=\bigl (\mathrm {Spa}(R_i,R_i^+),{\cal M}_i\bigr )$
to be a log affinoid perfectoid with initial object
![]() $U_0$
, and let
$U_0$
, and let
![]() $(R,R^+)$
be the p-adic completion of
$(R,R^+)$
be the p-adic completion of
![]() $\lim _i (R_i,R_i^+)$
. By assumption, we have a compatible system of
$\lim _i (R_i,R_i^+)$
. By assumption, we have a compatible system of
![]() $p^n$
-th roots
$p^n$
-th roots
![]() $Y_n$
of Y so that the system
$Y_n$
of Y so that the system
![]() $\underline {Y}:=[Y,Y_1,Y_2,\cdots ]\in \alpha ^{\flat ,+}\bigl ({\cal M}^{\flat ,+}\bigr )(U)$
. As shown in [Reference Andreatta and Iovita1, Lemma 3.25], we have
$\underline {Y}:=[Y,Y_1,Y_2,\cdots ]\in \alpha ^{\flat ,+}\bigl ({\cal M}^{\flat ,+}\bigr )(U)$
. As shown in [Reference Andreatta and Iovita1, Lemma 3.25], we have
![]() ${\cal O} \mathbb {A}_{\mathrm {log}}(U)= \mathbb {A}_{\mathrm {cris}}(R,R^+) \{\langle w-1 \rangle \}$
, which is the p-adic completion of the DP algebra
${\cal O} \mathbb {A}_{\mathrm {log}}(U)= \mathbb {A}_{\mathrm {cris}}(R,R^+) \{\langle w-1 \rangle \}$
, which is the p-adic completion of the DP algebra
![]() $\mathbb {A}_{\mathrm {cris}}(R,R^+) \langle w-1 \rangle $
. The structure as
$\mathbb {A}_{\mathrm {cris}}(R,R^+) \langle w-1 \rangle $
. The structure as
![]() $R_0$
-algebra is provided by sending
$R_0$
-algebra is provided by sending
![]() $Y\mapsto [\underline {Y}] w$
. Here,
$Y\mapsto [\underline {Y}] w$
. Here,
![]() $\mathbb {A}_{\mathrm {cris}}$
is the p-adic completion of the DP envelope of
$\mathbb {A}_{\mathrm {cris}}$
is the p-adic completion of the DP envelope of
![]() $ \mathbb {A}_{\mathrm {inf}}$
with respect to the kernel of
$ \mathbb {A}_{\mathrm {inf}}$
with respect to the kernel of
![]() $\vartheta $
. There is a similar description for
$\vartheta $
. There is a similar description for
![]() ${\cal O} \mathbb {A}_{\max ,n}^{\log }(U)$
.
${\cal O} \mathbb {A}_{\max ,n}^{\log }(U)$
.
There are also the geometric de Rham sheaves
![]() ${\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
and
${\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
and
![]() ${\cal O}\mathbb {B}_{\mathrm {dR, log}}$
defined in [Reference Diao, Lan, Liu and Zhu16, Def. 2.2.10], with a map
${\cal O}\mathbb {B}_{\mathrm {dR, log}}$
defined in [Reference Diao, Lan, Liu and Zhu16, Def. 2.2.10], with a map
![]() $\vartheta _{\mathrm {dR,log}}\colon {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+ \to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
and logarithmic connection
$\vartheta _{\mathrm {dR,log}}\colon {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+ \to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
and logarithmic connection
![]() ${\cal O}\mathbb {B}_{\mathrm {dR, log}}^+\longrightarrow {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+ \otimes _{{\cal O}^{\mathrm {unr,+}}_{\mathcal {X}_{{\mathrm {pke}}}}} \Omega ^{\mathrm {unr}}_{\mathcal {X}_{{\mathrm {pke}}}}$
(see [Reference Diao, Lan, Liu and Zhu16, §2.2]). As
${\cal O}\mathbb {B}_{\mathrm {dR, log}}^+\longrightarrow {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+ \otimes _{{\cal O}^{\mathrm {unr,+}}_{\mathcal {X}_{{\mathrm {pke}}}}} \Omega ^{\mathrm {unr}}_{\mathcal {X}_{{\mathrm {pke}}}}$
(see [Reference Diao, Lan, Liu and Zhu16, §2.2]). As
![]() ${\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
is an
${\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
is an
![]() $ {\cal O}_{{\mathcal {X}}_{\mathrm {pke}}}\otimes \mathbb {A}_{\mathrm {inf}}$
-algebra by construction, there is a natural map of sheaves
$ {\cal O}_{{\mathcal {X}}_{\mathrm {pke}}}\otimes \mathbb {A}_{\mathrm {inf}}$
-algebra by construction, there is a natural map of sheaves
![]() ${\cal O} \mathbb {A}_{\mathrm {inf}}\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
whose composite with
${\cal O} \mathbb {A}_{\mathrm {inf}}\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
whose composite with
![]() $\vartheta _{\mathrm {dR,log}}$
is
$\vartheta _{\mathrm {dR,log}}$
is
![]() $\vartheta _{\mathcal {X}}$
.
$\vartheta _{\mathcal {X}}$
.
Lemma 6.2. The map
![]() ${\cal O} \mathbb {A}_{\mathrm {inf}}\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
extends to morphisms
${\cal O} \mathbb {A}_{\mathrm {inf}}\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
extends to morphisms
![]() ${\cal O} \mathbb {A}_{\log }\to {\cal O}\mathbb {A}_{\max ,n}^{\log }\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
, for every n, such that the composite with
${\cal O} \mathbb {A}_{\log }\to {\cal O}\mathbb {A}_{\max ,n}^{\log }\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
, for every n, such that the composite with
![]() $\vartheta _{\mathrm {dR,log}}$
is the map
$\vartheta _{\mathrm {dR,log}}$
is the map
![]() $\vartheta _{\max ,n}$
and it is compatible with connections.
$\vartheta _{\max ,n}$
and it is compatible with connections.
Proof. First of all, we show how to get a map
![]() ${\cal O} \mathbb {A}_{\mathrm {inf}}'\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
of
${\cal O} \mathbb {A}_{\mathrm {inf}}'\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
of
![]() ${\cal O} \mathbb {A}_{\mathrm {inf}}$
-algebras.
${\cal O} \mathbb {A}_{\mathrm {inf}}$
-algebras.
It suffices to construct this for log affinoid perfectoid objects of
![]() $\mathcal {X}_{{\mathrm {pke}}}$
arising from toric charts, as those form a basis of
$\mathcal {X}_{{\mathrm {pke}}}$
arising from toric charts, as those form a basis of
![]() $\mathcal {X}_{{\mathrm {pke}}}$
. Take any such object that we denote by U. It follows from [Reference Diao, Lan, Liu and Zhu16, Lemma 2.3.12] that there exists a morphism of monoids
$\mathcal {X}_{{\mathrm {pke}}}$
. Take any such object that we denote by U. It follows from [Reference Diao, Lan, Liu and Zhu16, Lemma 2.3.12] that there exists a morphism of monoids
![]() $ \beta \colon {\cal M}^{\flat ,+}(U)^{\ast }\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+(U)$
such that for every
$ \beta \colon {\cal M}^{\flat ,+}(U)^{\ast }\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+(U)$
such that for every
![]() $a \in {\cal M}^{\flat ,+}(U)$
we have
$a \in {\cal M}^{\flat ,+}(U)$
we have
![]() $\alpha ^+(a^{\sharp })=\bigl [\alpha ^{\flat ,+}(a)\bigr ]\beta (a)$
. Since the map
$\alpha ^+(a^{\sharp })=\bigl [\alpha ^{\flat ,+}(a)\bigr ]\beta (a)$
. Since the map
![]() ${\cal M}^{\flat ,+}(U)\to {\cal M}^+(U)$
is an isomorphism, any element in the kernel H of
${\cal M}^{\flat ,+}(U)\to {\cal M}^+(U)$
is an isomorphism, any element in the kernel H of
![]() $(\alpha ^{\mathrm {unr}})^{\mathrm {gp}}(U)\times ( \alpha _{\mathrm {inf}})^{\mathrm {gp}}(U)\colon ({\cal M}^{\mathrm {unr, +}})^{\mathrm {gp}}(U) \times ({\cal M}^{\flat ,+})^{\mathrm {gp}}(U)\to ({\cal M}^+)^{\mathrm {gp}}(U)$
is of the form
$(\alpha ^{\mathrm {unr}})^{\mathrm {gp}}(U)\times ( \alpha _{\mathrm {inf}})^{\mathrm {gp}}(U)\colon ({\cal M}^{\mathrm {unr, +}})^{\mathrm {gp}}(U) \times ({\cal M}^{\flat ,+})^{\mathrm {gp}}(U)\to ({\cal M}^+)^{\mathrm {gp}}(U)$
is of the form
![]() $\bigl (a^{\sharp } (b^{\sharp })^{-1}, a b^{-1}\bigr )$
with
$\bigl (a^{\sharp } (b^{\sharp })^{-1}, a b^{-1}\bigr )$
with
![]() $a,b\in {\cal M}^{\flat }(U)$
such that
$a,b\in {\cal M}^{\flat }(U)$
such that
![]() $a^{\sharp }, b^{\sharp }\in {\cal M}^{\mathrm {unr, +}}(U)$
. Any such element can be sent to
$a^{\sharp }, b^{\sharp }\in {\cal M}^{\mathrm {unr, +}}(U)$
. Any such element can be sent to
![]() $\beta (a)\beta (b)^{-1}$
, and this defines a group homomorphism
$\beta (a)\beta (b)^{-1}$
, and this defines a group homomorphism
![]() $\beta \colon H\to {\cal M}^{\flat ,+}(U)^{\ast }$
. As
$\beta \colon H\to {\cal M}^{\flat ,+}(U)^{\ast }$
. As
![]() ${\cal M}'(U)= H \cdot \bigl ({\cal M}^{\mathrm {unr, +}}(U) \times {\cal M}^{\flat , +} (U)\bigr )\subset ({\cal M}^{\mathrm {unr, +}})^{\mathrm {gp}}(U) \times ({\cal M}^{\flat ,+})^{\mathrm { gp}}(U)\to ({\cal M}^+)^{\mathrm {gp}}(U)$
, such map extends to a map of monoids
${\cal M}'(U)= H \cdot \bigl ({\cal M}^{\mathrm {unr, +}}(U) \times {\cal M}^{\flat , +} (U)\bigr )\subset ({\cal M}^{\mathrm {unr, +}})^{\mathrm {gp}}(U) \times ({\cal M}^{\flat ,+})^{\mathrm { gp}}(U)\to ({\cal M}^+)^{\mathrm {gp}}(U)$
, such map extends to a map of monoids
![]() $\beta \colon {\cal M}'(U)\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+(U)$
which is compatible with the map
$\beta \colon {\cal M}'(U)\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+(U)$
which is compatible with the map
![]() $\alpha ^{\mathrm {unr}}(U)\times \alpha _{\mathrm {inf}}(U)\colon {\cal M}^{\mathrm {unr, +}}(U) \times {\cal M}^{\flat ,+}\to {\cal O} \mathbb {A}_{\mathrm {inf}}(U) \to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+(U)$
. Using this we get a unique morphism
$\alpha ^{\mathrm {unr}}(U)\times \alpha _{\mathrm {inf}}(U)\colon {\cal M}^{\mathrm {unr, +}}(U) \times {\cal M}^{\flat ,+}\to {\cal O} \mathbb {A}_{\mathrm {inf}}(U) \to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+(U)$
. Using this we get a unique morphism
![]() ${\cal O} \mathbb {A}_{\mathrm {inf}}'(U) \to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+(U)$
of
${\cal O} \mathbb {A}_{\mathrm {inf}}'(U) \to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+(U)$
of
![]() ${\cal O} \mathbb {A}_{\mathrm {inf}}(U)$
-algebras which coincides with
${\cal O} \mathbb {A}_{\mathrm {inf}}(U)$
-algebras which coincides with
![]() $\beta $
on
$\beta $
on
![]() ${\cal M}'(U)$
.
${\cal M}'(U)$
.
In this way, we get the claimed morphism
![]() ${\cal O} \mathbb {A}_{\mathrm {inf}}'\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
whose composite with
${\cal O} \mathbb {A}_{\mathrm {inf}}'\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
whose composite with
![]() $\vartheta _{\mathrm {dR,log}}$
is
$\vartheta _{\mathrm {dR,log}}$
is
![]() $\vartheta _{\mathcal {X}}'$
. In particular, the kernel
$\vartheta _{\mathcal {X}}'$
. In particular, the kernel
![]() $\mathcal {I}$
of
$\mathcal {I}$
of
![]() $\vartheta _{\mathcal {X}}'$
is mapped to the kernel of
$\vartheta _{\mathcal {X}}'$
is mapped to the kernel of
![]() $\vartheta _{\mathrm {dR,log}}$
. As p is invertible in
$\vartheta _{\mathrm {dR,log}}$
. As p is invertible in
![]() ${\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
, it also extends to a morphism
${\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
, it also extends to a morphism
![]() $\displaystyle {\cal O} \mathbb {A}_{\mathrm {inf}}' \bigl [\frac {\mathcal {I}}{p^n}\bigr ]\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
and
$\displaystyle {\cal O} \mathbb {A}_{\mathrm {inf}}' \bigl [\frac {\mathcal {I}}{p^n}\bigr ]\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
and
![]() $\displaystyle \frac {\mathcal {I}}{p^n}$
maps to the kernel of
$\displaystyle \frac {\mathcal {I}}{p^n}$
maps to the kernel of
![]() $\vartheta _{\mathrm {dR,log}}$
. Passing to log affinoid perfectoid objects of
$\vartheta _{\mathrm {dR,log}}$
. Passing to log affinoid perfectoid objects of
![]() $\mathcal {X}_{{\mathrm {pke}}}$
one shows that such map extends to the p-adic completion
$\mathcal {X}_{{\mathrm {pke}}}$
one shows that such map extends to the p-adic completion
![]() $\displaystyle {\cal O} \mathbb {A}_{\max ,n}^{\log }$
of
$\displaystyle {\cal O} \mathbb {A}_{\max ,n}^{\log }$
of
![]() $\displaystyle {\cal O} \mathbb {A}_{\mathrm {inf}}' \bigl [\frac {\mathcal {I}}{p^n}\bigr ] \to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
. The compatibility with
$\displaystyle {\cal O} \mathbb {A}_{\mathrm {inf}}' \bigl [\frac {\mathcal {I}}{p^n}\bigr ] \to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
. The compatibility with
![]() $\vartheta _{\max ,n}$
is clear. The compatibility of the connections is also clear as both are defined using the derivation
$\vartheta _{\max ,n}$
is clear. The compatibility of the connections is also clear as both are defined using the derivation
![]() $d\colon {\cal O}_{\widehat {X}} \to \Omega ^{\log }_{{\widehat {X}}/{\cal O}_K}$
.
$d\colon {\cal O}_{\widehat {X}} \to \Omega ^{\log }_{{\widehat {X}}/{\cal O}_K}$
.
6.2 Crystalline comparison morphisms
We have a crystalline comparison morphism over
![]() $\mathcal {X}_{{\mathrm {pke}}}$
:
$\mathcal {X}_{{\mathrm {pke}}}$
:
where
![]() $(T_p (E))^{\vee }$
is the
$(T_p (E))^{\vee }$
is the
![]() ${\mathbb Z}_p$
-dual of
${\mathbb Z}_p$
-dual of
![]() $T_p (E)$
and
$T_p (E)$
and
![]() $\nabla '$
is the natural connection on
$\nabla '$
is the natural connection on
![]() $\mathrm {H}^1_{\mathrm {crys}}\bigl (E_0/\widehat {X}\bigr )\otimes {\cal O}\mathbb {A}_{\mathrm {log}}$
determined by the connections on the factors. We also write
$\mathrm {H}^1_{\mathrm {crys}}\bigl (E_0/\widehat {X}\bigr )\otimes {\cal O}\mathbb {A}_{\mathrm {log}}$
determined by the connections on the factors. We also write
to ease the notation.
We describe
![]() $\alpha _{\mathrm {log}}$
for a log affinoid perfectoid open cover of
$\alpha _{\mathrm {log}}$
for a log affinoid perfectoid open cover of
![]() $\mathcal {X}$
. Consider an étale open
$\mathcal {X}$
. Consider an étale open
![]() $U=\mathrm {Spf}(S)\subset \widehat {X}$
. Let
$U=\mathrm {Spf}(S)\subset \widehat {X}$
. Let
![]() $W=\mathrm {Spa}(R,R^+)$
be a log affinoid perfectoid cover of
$W=\mathrm {Spa}(R,R^+)$
be a log affinoid perfectoid cover of
![]() $U_{\overline {{\mathbb Q}}_p}$
, the adic geometric generic fibre of U. We assume that the universal elliptic curve extends to a (generalised) elliptic curve
$U_{\overline {{\mathbb Q}}_p}$
, the adic geometric generic fibre of U. We assume that the universal elliptic curve extends to a (generalised) elliptic curve
![]() $\widetilde {E}$
over
$\widetilde {E}$
over
![]() $\mbox {Spec} (S)$
and that
$\mbox {Spec} (S)$
and that
![]() $T_p(E)$
is trivialized over W. Consider the rings
$T_p(E)$
is trivialized over W. Consider the rings
![]() $A_{\mathrm {cris}}(R^+)$
(resp.
$A_{\mathrm {cris}}(R^+)$
(resp.
![]() $A_{\mathrm {log}}(R^+)$
) defined by taking the p-adic completion of the DP envelope (resp. the log DP envelope) of
$A_{\mathrm {log}}(R^+)$
) defined by taking the p-adic completion of the DP envelope (resp. the log DP envelope) of
![]() $S\otimes \mathbb {A}_{\mathrm {inf}}(W)$
with respect to the kernel of the map
$S\otimes \mathbb {A}_{\mathrm {inf}}(W)$
with respect to the kernel of the map
![]() $1\otimes \vartheta (W)\colon S\otimes \mathbb {A}_{\mathrm {inf}}(W)\to \widehat {{\cal O}}_{\mathcal {X}}^+(W)=R^+$
. It naturally maps to
$1\otimes \vartheta (W)\colon S\otimes \mathbb {A}_{\mathrm {inf}}(W)\to \widehat {{\cal O}}_{\mathcal {X}}^+(W)=R^+$
. It naturally maps to
![]() ${\cal O} \mathbb {A}_{\mathrm { log}}(W)$
. We define
${\cal O} \mathbb {A}_{\mathrm { log}}(W)$
. We define
![]() $\alpha _{\mathrm {log}}(W)$
with values in
$\alpha _{\mathrm {log}}(W)$
with values in
![]() $\mathrm {H}^1_{\mathrm {crys}}\bigl (\widetilde {E}_0/S\bigr ) \otimes _S A_{\mathrm {log}}(R^+)$
as follows.
$\mathrm {H}^1_{\mathrm {crys}}\bigl (\widetilde {E}_0/S\bigr ) \otimes _S A_{\mathrm {log}}(R^+)$
as follows.
Away from the cusps: Assume first that
![]() $\widetilde {E}$
is an elliptic curve so that
$\widetilde {E}$
is an elliptic curve so that
![]() $\widetilde {E}[p^n](R^+)=E[p^n](R)$
for every
$\widetilde {E}[p^n](R^+)=E[p^n](R)$
for every
![]() $n\in \ N$
and
$n\in \ N$
and
![]() $T_p (\widetilde {E})(R^+)=T_p(E)(R)$
. Equivalently, the log structure is trivial and
$T_p (\widetilde {E})(R^+)=T_p(E)(R)$
. Equivalently, the log structure is trivial and
![]() $A_{\mathrm {log}}(R^+)=A_{\mathrm {cris}}(R^+)$
. Then to give
$A_{\mathrm {log}}(R^+)=A_{\mathrm {cris}}(R^+)$
. Then to give
![]() $a \in T_p(E^{\vee })(R)=T_p \bigl (E\bigr )^{\vee }(R^+)(1)$
is equivalent to give a map of p-divisible groups
$a \in T_p(E^{\vee })(R)=T_p \bigl (E\bigr )^{\vee }(R^+)(1)$
is equivalent to give a map of p-divisible groups
![]() $\gamma _a\colon {\mathbb Q}_p/{\mathbb Z}_p \to E^{\vee }[ p^{\infty }]$
over
$\gamma _a\colon {\mathbb Q}_p/{\mathbb Z}_p \to E^{\vee }[ p^{\infty }]$
over
![]() $R^+$
and
$R^+$
and
![]() $\gamma _a$
defines a map of covariant Dieudonné modules
$\gamma _a$
defines a map of covariant Dieudonné modules
Note that
![]() $A_{\mathrm { cris}}(R^+)=\textbf {D}_{\mathrm {cris}}({\mathbb Q}_p/{\mathbb Z}_p )\bigl (A_{\mathrm {cris}}(R^+)\bigr )$
and
$A_{\mathrm { cris}}(R^+)=\textbf {D}_{\mathrm {cris}}({\mathbb Q}_p/{\mathbb Z}_p )\bigl (A_{\mathrm {cris}}(R^+)\bigr )$
and
![]() $\textbf {D}_{\mathrm { cris}}\bigl (\widetilde {E}^{\vee }[ p^{\infty }]\bigr )\bigl (A_{\mathrm {cris}}(R^+)\bigr )=\mathrm {H}^1_{\mathrm {crys}}\bigl (E^{\vee }_0/S\bigr )^{\vee }\otimes _S A_{\mathrm {cris}}(R^+) $
, where
$\textbf {D}_{\mathrm { cris}}\bigl (\widetilde {E}^{\vee }[ p^{\infty }]\bigr )\bigl (A_{\mathrm {cris}}(R^+)\bigr )=\mathrm {H}^1_{\mathrm {crys}}\bigl (E^{\vee }_0/S\bigr )^{\vee }\otimes _S A_{\mathrm {cris}}(R^+) $
, where
![]() $E^{\vee }_0$
is the modulo p reduction of
$E^{\vee }_0$
is the modulo p reduction of
![]() $E^{\vee }$
. Thus
$E^{\vee }$
. Thus
![]() $\textbf {D}_{\mathrm {cris}}(\gamma _a)$
defines a map
$\textbf {D}_{\mathrm {cris}}(\gamma _a)$
defines a map
and setting
(see [Reference Scholze and Weinstein24]§3.5) and using Weil, respectively Poincaré dualities gives the map
As
![]() $\textbf {D}_{\mathrm {cris}}(\gamma _a)$
is a map of crystals; therefore, it is compatible with connections. Since
$\textbf {D}_{\mathrm {cris}}(\gamma _a)$
is a map of crystals; therefore, it is compatible with connections. Since
![]() $\nabla (1)=0$
for
$\nabla (1)=0$
for
![]() $1\in A_{\mathrm { cris}}(R^+)$
, then
$1\in A_{\mathrm { cris}}(R^+)$
, then
![]() $\nabla '\Bigl ( \mathrm {Im}\bigl (\alpha _{\mathrm {cris}}(W)\bigr )\Bigr )=0$
.
$\nabla '\Bigl ( \mathrm {Im}\bigl (\alpha _{\mathrm {cris}}(W)\bigr )\Bigr )=0$
.
Around the cusps: Assume next that U does not contain supersingular points. Then the connected part
![]() $\widetilde {E}[p^{\infty }]^0$
of
$\widetilde {E}[p^{\infty }]^0$
of
![]() $\widetilde {E}[p^{\infty }]$
is a p-divisble group of multiplicative type. Let
$\widetilde {E}[p^{\infty }]$
is a p-divisble group of multiplicative type. Let
![]() $\widetilde {E}[p^{\infty }]^{0,\vee }$
be its Cartier dual; it is an étale p-divisible group over U. We write
$\widetilde {E}[p^{\infty }]^{0,\vee }$
be its Cartier dual; it is an étale p-divisible group over U. We write
![]() $\mathrm {H}^1_{\mathrm {crys}}(E_0/S)$
for the direct sum of
$\mathrm {H}^1_{\mathrm {crys}}(E_0/S)$
for the direct sum of
![]() $\omega _{E/S}\cong \textbf {D}_{\mathrm { cris}}\bigl (\widetilde {E}[ p^{\infty }]^{0}\bigr )(S)^{\vee }$
and
$\omega _{E/S}\cong \textbf {D}_{\mathrm { cris}}\bigl (\widetilde {E}[ p^{\infty }]^{0}\bigr )(S)^{\vee }$
and
![]() $\omega _{E/S}^{-1} \cong \textbf {D}_{\mathrm {cris}}\bigl (\widetilde {E}[ p^{\infty }]^{0,\vee }\bigr )(S)^{\vee }$
. The connection
$\omega _{E/S}^{-1} \cong \textbf {D}_{\mathrm {cris}}\bigl (\widetilde {E}[ p^{\infty }]^{0,\vee }\bigr )(S)^{\vee }$
. The connection
![]() $\mathrm {H}^1_{\mathrm {crys}}(E_0/S)\to \mathrm {H}^1_{\mathrm {crys}}(E_0/S)\otimes _S \Omega ^{1,\log }_{S/{\cal O}_K}$
is the sum of the connections induced from those on
$\mathrm {H}^1_{\mathrm {crys}}(E_0/S)\to \mathrm {H}^1_{\mathrm {crys}}(E_0/S)\otimes _S \Omega ^{1,\log }_{S/{\cal O}_K}$
is the sum of the connections induced from those on
![]() $\textbf {D}_{\mathrm {cris}}\bigl (\widetilde {E}[ p^{\infty }]^0\bigr )(S)^{\vee }$
and
$\textbf {D}_{\mathrm {cris}}\bigl (\widetilde {E}[ p^{\infty }]^0\bigr )(S)^{\vee }$
and
![]() $\textbf {D}_{\mathrm {cris}}\bigl (\widetilde {E}[ p^{\infty }]^{0,\vee }\bigr )(S)^{\vee }$
plus the S-linear isomorphism
$\textbf {D}_{\mathrm {cris}}\bigl (\widetilde {E}[ p^{\infty }]^{0,\vee }\bigr )(S)^{\vee }$
plus the S-linear isomorphism
![]() $\omega _{E/S} \cong \omega _{E/S}^{-1} \otimes _S \Omega ^{1,\log }_{S/{\cal O}_{K}}$
provided by the Kodaira–Spencer isomorphism, which we denote
$\omega _{E/S} \cong \omega _{E/S}^{-1} \otimes _S \Omega ^{1,\log }_{S/{\cal O}_{K}}$
provided by the Kodaira–Spencer isomorphism, which we denote
![]() $\mathrm {KS}$
. In other words, as a module
$\mathrm {KS}$
. In other words, as a module
![]() $\textbf {D}_{\mathrm {cris}}(\widetilde {E}[p^{\infty }])$
is isomorphic to the direct sum
$\textbf {D}_{\mathrm {cris}}(\widetilde {E}[p^{\infty }])$
is isomorphic to the direct sum
![]() $\textbf {D}_{\mathrm { cris}}(\widetilde {E}[p^{\infty }]^{0})(S)^{\vee }\oplus \textbf {D}_{\mathrm {cris}}(\widetilde {E}[p^{\infty }]^{0,\vee })(S)^{\vee }\cong \omega _{E/S}\oplus \omega ^{-1}_{E/S}$
, while the logarithmic connection
$\textbf {D}_{\mathrm { cris}}(\widetilde {E}[p^{\infty }]^{0})(S)^{\vee }\oplus \textbf {D}_{\mathrm {cris}}(\widetilde {E}[p^{\infty }]^{0,\vee })(S)^{\vee }\cong \omega _{E/S}\oplus \omega ^{-1}_{E/S}$
, while the logarithmic connection
![]() $\nabla _{\widetilde {E}[p^{\infty }]}$
is given with respect to this decomposition by
$\nabla _{\widetilde {E}[p^{\infty }]}$
is given with respect to this decomposition by
 $$ \begin{align*} \left( \begin{array}{cc} \nabla_{\widetilde{E}[p^{\infty}]^0} & 0 \\ \mathrm{KS} & \nabla_{\widetilde{E}[p^{\infty}]^{0,\vee}}\end{array}\right). \end{align*} $$
$$ \begin{align*} \left( \begin{array}{cc} \nabla_{\widetilde{E}[p^{\infty}]^0} & 0 \\ \mathrm{KS} & \nabla_{\widetilde{E}[p^{\infty}]^{0,\vee}}\end{array}\right). \end{align*} $$
Lemma 6.3. If U does not contain supersingular points and
![]() $\widetilde {E}$
is an elliptic curve, the two definitions of
$\widetilde {E}$
is an elliptic curve, the two definitions of
![]() $\mathrm {H}^1_{\mathrm {crys}}(E_0/S)$
coincide. Moreover, a splitting of the Tate module
$\mathrm {H}^1_{\mathrm {crys}}(E_0/S)$
coincide. Moreover, a splitting of the Tate module
![]() $T_p\big (\widetilde {E}[p^{\infty }])(R)=T_p\bigl (\widetilde {E}[p^{\infty }]^{0}\bigr )(R^+)\oplus T_p\bigl (\widetilde {E}[p^{\infty }]^{0,\vee }\bigr )(R^+)$
uniquely defines
$T_p\big (\widetilde {E}[p^{\infty }])(R)=T_p\bigl (\widetilde {E}[p^{\infty }]^{0}\bigr )(R^+)\oplus T_p\bigl (\widetilde {E}[p^{\infty }]^{0,\vee }\bigr )(R^+)$
uniquely defines
-
(1) a splitting
 $\widetilde {E}[p^{\infty }]_{R^+}=\widetilde {E}[p^{\infty }]^{0,\vee }_{R^+}\oplus \widetilde {E}[p^{\infty }]^{0}_{R^+}$
of the connected-étale sequence for
$\widetilde {E}[p^{\infty }]_{R^+}=\widetilde {E}[p^{\infty }]^{0,\vee }_{R^+}\oplus \widetilde {E}[p^{\infty }]^{0}_{R^+}$
of the connected-étale sequence for
 $\widetilde {E}[p^{\infty }]_{R^+}$
;
$\widetilde {E}[p^{\infty }]_{R^+}$
; -
(2) a splitting of
 $\textbf {D}_{\mathrm {cris}}\bigl (\widetilde {E}^{\vee }[ p^{\infty }]\bigr )\bigl (A_{\mathrm {cris}}(R^+)\bigr )^{\vee }\cong \mathrm {H}^1_{\mathrm { crys}}\bigl (E_0/S\bigr )^{\vee }\otimes _S A_{\mathrm {cris}}(R^+) $
;
$\textbf {D}_{\mathrm {cris}}\bigl (\widetilde {E}^{\vee }[ p^{\infty }]\bigr )\bigl (A_{\mathrm {cris}}(R^+)\bigr )^{\vee }\cong \mathrm {H}^1_{\mathrm { crys}}\bigl (E_0/S\bigr )^{\vee }\otimes _S A_{\mathrm {cris}}(R^+) $
; -
(3) a splitting of
 $\alpha _{\mathrm {log}}(W)$
as the direct sum of the crystalline comparison maps for the p-divisible groups
$\alpha _{\mathrm {log}}(W)$
as the direct sum of the crystalline comparison maps for the p-divisible groups
 $\widetilde {E}[p^{\infty }]^0_{R^+}$
and
$\widetilde {E}[p^{\infty }]^0_{R^+}$
and
 $\widetilde {E}[p^{\infty }]^{0,\vee }_{R^+}$
, compatibly with (1) ad (2).
$\widetilde {E}[p^{\infty }]^{0,\vee }_{R^+}$
, compatibly with (1) ad (2).
Proof. Notice that the quotient map
![]() $\widetilde {E}^{\vee }[p^{\infty }] \to \widetilde {E}^{\vee }[p^{\infty }]^{\mathrm {et}} $
onto the étale part induces a map from
$\widetilde {E}^{\vee }[p^{\infty }] \to \widetilde {E}^{\vee }[p^{\infty }]^{\mathrm {et}} $
onto the étale part induces a map from
![]() $\mathrm {H}^1_{\mathrm {crys}}\bigl (\widetilde {E}_0/S\bigr )$
to the Dieudonné module of
$\mathrm {H}^1_{\mathrm {crys}}\bigl (\widetilde {E}_0/S\bigr )$
to the Dieudonné module of
![]() $\widetilde {E}^{\vee }[p^{\infty }]^{\mathrm { et}}(S)$
which splits canonically via the unit root decomposition. As
$\widetilde {E}^{\vee }[p^{\infty }]^{\mathrm { et}}(S)$
which splits canonically via the unit root decomposition. As
![]() $\widetilde {E}^{\vee }[p^{\infty }]^{\mathrm {et}}\cong \widetilde {E}[p^{\infty }]^{0,\vee }$
and similarly
$\widetilde {E}^{\vee }[p^{\infty }]^{\mathrm {et}}\cong \widetilde {E}[p^{\infty }]^{0,\vee }$
and similarly
![]() $\widetilde {E}^{\vee }[p^{\infty }]^{0}\cong \widetilde {E}[p^{\infty }]^{\mathrm {et,\vee }}\cong \widetilde {E}[p^{\infty }]^0$
we conclude that
$\widetilde {E}^{\vee }[p^{\infty }]^{0}\cong \widetilde {E}[p^{\infty }]^{\mathrm {et,\vee }}\cong \widetilde {E}[p^{\infty }]^0$
we conclude that
![]() $\mathrm {H}^1_{\mathrm {crys}}\bigl (\widetilde {E}_0/S\bigr )$
splits canonically, as a module, as the direct sum of
$\mathrm {H}^1_{\mathrm {crys}}\bigl (\widetilde {E}_0/S\bigr )$
splits canonically, as a module, as the direct sum of
![]() $\omega _{E/S}\cong \textbf {D}_{\mathrm {cris}}\bigl (\widetilde {E}[ p^{\infty }]^{0}\bigr )(S)^{\vee }$
and
$\omega _{E/S}\cong \textbf {D}_{\mathrm {cris}}\bigl (\widetilde {E}[ p^{\infty }]^{0}\bigr )(S)^{\vee }$
and
![]() $\omega _{E/S}^{-1}\cong \textbf {D}_{\mathrm {cris}}\bigl (\widetilde {E}[ p^{\infty }]^{0,\vee }\bigr )(S)^{\vee }$
, with connection given by the connection on each factor plus the Kodaira–Spencer isomorphism. Thus, the two descriptions of
$\omega _{E/S}^{-1}\cong \textbf {D}_{\mathrm {cris}}\bigl (\widetilde {E}[ p^{\infty }]^{0,\vee }\bigr )(S)^{\vee }$
, with connection given by the connection on each factor plus the Kodaira–Spencer isomorphism. Thus, the two descriptions of
![]() $\mathrm {H}^1_{\mathrm {crys}}\bigl (\widetilde {E}_0/S\bigr )$
coincide. Claims (2) and (3) follow from the functoriality of
$\mathrm {H}^1_{\mathrm {crys}}\bigl (\widetilde {E}_0/S\bigr )$
coincide. Claims (2) and (3) follow from the functoriality of
![]() $\textbf {D}_{\mathrm {cris}}$
and of
$\textbf {D}_{\mathrm {cris}}$
and of
![]() $\alpha _{\mathrm {log}}$
.
$\alpha _{\mathrm {log}}$
.
Lemma 6.3 suggests how to define
![]() $\alpha _{\mathrm {log}}(W)$
in the case that U does not contain supersingular points but can possibly contain the cusps. Namely, we write
$\alpha _{\mathrm {log}}(W)$
in the case that U does not contain supersingular points but can possibly contain the cusps. Namely, we write
![]() $T_p\big (\widetilde {E}[p^{\infty }])(R)$
as a split extension of
$T_p\big (\widetilde {E}[p^{\infty }])(R)$
as a split extension of
![]() $T_p\bigl (\widetilde {E}[p^{\infty }]^{0,\vee }\bigr )(R^+)$
by
$T_p\bigl (\widetilde {E}[p^{\infty }]^{0,\vee }\bigr )(R^+)$
by
![]() $T_p\bigl (\widetilde {E}[p^{\infty }]^{0}\bigr )(R^+)$
and
$T_p\bigl (\widetilde {E}[p^{\infty }]^{0}\bigr )(R^+)$
and
![]() $\alpha _{\mathrm {log}}(W)$
as the direct sum of the crystalline comparison maps for the p-divisible groups
$\alpha _{\mathrm {log}}(W)$
as the direct sum of the crystalline comparison maps for the p-divisible groups
![]() $\widetilde {E}[p^{\infty }]^0_{R^+}$
and
$\widetilde {E}[p^{\infty }]^0_{R^+}$
and
![]() $\widetilde {E}[p^{\infty }]^{0,\vee }_{R^+}$
. Then Lemma 6.3 implies that this definition agreed with the definition given away from the cusps. Thus,
$\widetilde {E}[p^{\infty }]^{0,\vee }_{R^+}$
. Then Lemma 6.3 implies that this definition agreed with the definition given away from the cusps. Thus,
![]() $\alpha _{\mathrm {log}}(W)$
are functorial in the pair
$\alpha _{\mathrm {log}}(W)$
are functorial in the pair
![]() $(U,W)$
, and hence, they glue to a morphism
$(U,W)$
, and hence, they glue to a morphism
![]() $\alpha _{\mathrm {log }}$
on
$\alpha _{\mathrm {log }}$
on
![]() $\mathcal {X}_{{\mathrm {pke}}}$
. We also consider the composite map of sheaves
$\mathcal {X}_{{\mathrm {pke}}}$
. We also consider the composite map of sheaves
induced by composing
![]() $\alpha _{\mathrm {log}}$
with the map of sheaves
$\alpha _{\mathrm {log}}$
with the map of sheaves
![]() ${\cal O} \mathbb {A}_{\mathrm { log}} \to {\cal O} \mathbb {A}_{\mathrm {max, n}}^{\mathrm {log}}$
described at the beginning of the section.
${\cal O} \mathbb {A}_{\mathrm { log}} \to {\cal O} \mathbb {A}_{\mathrm {max, n}}^{\mathrm {log}}$
described at the beginning of the section.
6.3 The sheaves
 $\mathbf {W}_{k, \mathrm {dR}}$
$\mathbf {W}_{k, \mathrm {dR}}$
We consider strict neighbourhoods
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
of the ordinary locus in
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
of the ordinary locus in
![]() $\mathcal {X}$
, where
$\mathcal {X}$
, where
![]() $\mathrm {Ha}$
is a (any) local lift of the Hasse invariant. It follows from [Reference Scholze23, Lemma 3.3.8 & Lemma 3.3.15] that the neighbourhoods
$\mathrm {Ha}$
is a (any) local lift of the Hasse invariant. It follows from [Reference Scholze23, Lemma 3.3.8 & Lemma 3.3.15] that the neighbourhoods
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )\otimes _{K} {\mathbb C}_p$
and
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )\otimes _{K} {\mathbb C}_p$
and
![]() $\mathcal {X}_{\infty }^{(m)}$
of §4.2 for varying s, respectively m, are fundamental systems of open neighbourhoods of the ordinary locus of
$\mathcal {X}_{\infty }^{(m)}$
of §4.2 for varying s, respectively m, are fundamental systems of open neighbourhoods of the ordinary locus of
![]() $\mathcal {X}_{{\mathbb C}_p}$
. We then take s and m large enough so that the conclusions of Proposition 4.5 hold for
$\mathcal {X}_{{\mathbb C}_p}$
. We then take s and m large enough so that the conclusions of Proposition 4.5 hold for
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
and for
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
and for
![]() $\mathcal {X}_{\infty }^{(m)}$
. Namely, we require that a canonical subgroup
$\mathcal {X}_{\infty }^{(m)}$
. Namely, we require that a canonical subgroup
![]() $C_n$
of order
$C_n$
of order
![]() $p^n$
exists, and this defines a section
$p^n$
exists, and this defines a section
of the natural forgetful map
![]() $\mathcal {X}_0(p^n,N)\bigl (p/\mathrm {Ha}^{p^s}\bigr )\longrightarrow \mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
. Write
$\mathcal {X}_0(p^n,N)\bigl (p/\mathrm {Ha}^{p^s}\bigr )\longrightarrow \mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
. Write
for the
![]() $({\mathbb Z}/p^n{\mathbb Z})^{\ast }$
-Galois cover classifying trivializations of
$({\mathbb Z}/p^n{\mathbb Z})^{\ast }$
-Galois cover classifying trivializations of
![]() $C_n^{\vee }$
.
$C_n^{\vee }$
.
Let E be the universal elliptic curve over the normalization of
![]() $\widehat {X}$
in
$\widehat {X}$
in
![]() ${{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
. Its invariant differentials
${{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
. Its invariant differentials
![]() $\omega _E$
and relative de Rham cohomology
$\omega _E$
and relative de Rham cohomology
![]() $\mathrm {H}_E$
define locally free
$\mathrm {H}_E$
define locally free
![]() ${\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
-modules with the Hodge filtration
${\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
-modules with the Hodge filtration
![]() $\omega _E\subset \mathrm {H}_E$
. Write
$\omega _E\subset \mathrm {H}_E$
. Write
![]() $\underline {\delta }$
for the invertible
$\underline {\delta }$
for the invertible
![]() ${\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
-module defined by
${\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
-module defined by
![]() $\underline {\delta }:=\omega _E(\omega _E^{\mathrm {mod}})^{-1}$
. Note that
$\underline {\delta }:=\omega _E(\omega _E^{\mathrm {mod}})^{-1}$
. Note that
![]() $\underline {\delta }^{p-1}= \nu ^{\ast }(\mathrm {Hdg})$
, where
$\underline {\delta }^{p-1}= \nu ^{\ast }(\mathrm {Hdg})$
, where
![]() $\mathrm {Hdg}$
is the ideal of
$\mathrm {Hdg}$
is the ideal of
![]() ${\cal O}_{\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
generated by the local lifts
${\cal O}_{\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
generated by the local lifts
![]() $\mathrm {Ha}$
of the Hasse invariant (due to the blowup, it does not depend on the choice of the local lifts).
$\mathrm {Ha}$
of the Hasse invariant (due to the blowup, it does not depend on the choice of the local lifts).
From the tautological section P of
![]() $C_n^{\vee }$
, we get a canonical section t of
$C_n^{\vee }$
, we get a canonical section t of
![]() $\omega _E^{\mathrm {mod}}/p^r \omega _E^{\mathrm {mod}}$
generating it as
$\omega _E^{\mathrm {mod}}/p^r \omega _E^{\mathrm {mod}}$
generating it as
![]() ${\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
-module. Recall that
${\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
-module. Recall that
![]() $k\colon {\mathbb Z}_p^{\ast } \to B^{\ast }$
is an r-analytic character for
$k\colon {\mathbb Z}_p^{\ast } \to B^{\ast }$
is an r-analytic character for
![]() $r\leq n$
, where B is a ring as in definition 3.6. We denote by
$r\leq n$
, where B is a ring as in definition 3.6. We denote by
![]() $\mathrm {H}_E^{\#}$
the pushout in the category of
$\mathrm {H}_E^{\#}$
the pushout in the category of
![]() ${\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
-modules of the diagram
${\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
-modules of the diagram
 $$ \begin{align*} \begin{array}{cccccccccc} \underline{\delta}^p\omega_E&\longrightarrow&\underline{\delta}^p\mathrm{H}_{E}\\ \cap\\ \omega_{E}^{\mathrm{mod}}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{cccccccccc} \underline{\delta}^p\omega_E&\longrightarrow&\underline{\delta}^p\mathrm{H}_{E}\\ \cap\\ \omega_{E}^{\mathrm{mod}}. \end{array} \end{align*} $$
We then have the following commutative diagram of sheaves with exact rows:
 $$ \begin{align*} \begin{array}{ccccccccc} 0&\longrightarrow&\underline{\delta}^p\omega_E&\longrightarrow&\underline{\delta}^p\mathrm{H}_{E}&\longrightarrow&\underline{\delta}^p\omega_{E}^{-1}&\longrightarrow&0\\ &&\cap&&\downarrow&&||\\ 0&\longrightarrow&\omega_{E}^{\mathrm{mod}}&\longrightarrow&\mathrm{H}_{E}^{\#}&\longrightarrow&\underline{\delta}^p\omega_{E}^{-1}&\longrightarrow&0\\ &&\cap&&\cap&&\cap\\ 0&\longrightarrow&\omega_{E}&\longrightarrow&\mathrm{H}_{E}&\longrightarrow&\omega_E^{-1}&\longrightarrow&0. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ccccccccc} 0&\longrightarrow&\underline{\delta}^p\omega_E&\longrightarrow&\underline{\delta}^p\mathrm{H}_{E}&\longrightarrow&\underline{\delta}^p\omega_{E}^{-1}&\longrightarrow&0\\ &&\cap&&\downarrow&&||\\ 0&\longrightarrow&\omega_{E}^{\mathrm{mod}}&\longrightarrow&\mathrm{H}_{E}^{\#}&\longrightarrow&\underline{\delta}^p\omega_{E}^{-1}&\longrightarrow&0\\ &&\cap&&\cap&&\cap\\ 0&\longrightarrow&\omega_{E}&\longrightarrow&\mathrm{H}_{E}&\longrightarrow&\omega_E^{-1}&\longrightarrow&0. \end{array} \end{align*} $$
It follows that
![]() $\mathrm {H}_E^{\#}$
is a locally free
$\mathrm {H}_E^{\#}$
is a locally free
![]() ${\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^r}\bigr )}^+$
-module of rank two and
${\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^r}\bigr )}^+$
-module of rank two and
![]() $(\omega _E^{\mathrm {mod}}, t)\subset (\mathrm {H}_E^{\#}, t)$
is a compatible inclusion of locally free sheaves with marked sections.
$(\omega _E^{\mathrm {mod}}, t)\subset (\mathrm {H}_E^{\#}, t)$
is a compatible inclusion of locally free sheaves with marked sections.
Using the formalism of the dual VBMS (see §3.3), we get sheaves of
![]() ${\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+\widehat {\otimes } B$
-modules
${\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+\widehat {\otimes } B$
-modules
![]() $\omega _E^k \subset \mathbf {W}_{k, \mathrm {dR}}$
. We have a residual action of the Galois group
$\omega _E^k \subset \mathbf {W}_{k, \mathrm {dR}}$
. We have a residual action of the Galois group
![]() $({\mathbb Z}/p^n{\mathbb Z})^{\ast }$
of
$({\mathbb Z}/p^n{\mathbb Z})^{\ast }$
of
![]() $j_n\colon {{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )\to \mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
on
$j_n\colon {{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )\to \mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
on
![]() $(\omega _E^{\mathrm {mod}}, t)$
and
$(\omega _E^{\mathrm {mod}}, t)$
and
![]() $ (\mathrm {H}_E^{\#}, t)$
on which it acts by scalar multiplication. We then get sheaves
$ (\mathrm {H}_E^{\#}, t)$
on which it acts by scalar multiplication. We then get sheaves
![]() $\omega _E^k\subset \mathbf {W}_{k, \mathrm {dR}}$
of
$\omega _E^k\subset \mathbf {W}_{k, \mathrm {dR}}$
of
![]() ${\cal O}_{\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )}\widehat {\otimes } B$
-modules by taking the subsheaves of
${\cal O}_{\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )}\widehat {\otimes } B$
-modules by taking the subsheaves of
![]() $j_{n,\ast }(\omega _E^k)\subset j_{n,\ast }(\mathbf {W}_{k, \mathrm {dR}})$
on which
$j_{n,\ast }(\omega _E^k)\subset j_{n,\ast }(\mathbf {W}_{k, \mathrm {dR}})$
on which
![]() ${\mathbb Z}_p^{\ast }$
acts via k. We refer to [Reference Andreatta and Iovita2, §3.2& 3.3] for details.
${\mathbb Z}_p^{\ast }$
acts via k. We refer to [Reference Andreatta and Iovita2, §3.2& 3.3] for details.
Proposition 6.4. The base change of
![]() $\omega _E^k[1/p]$
to
$\omega _E^k[1/p]$
to
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )_{{\mathbb C}_p}$
coincides with the restriction of the sheaf
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )_{{\mathbb C}_p}$
coincides with the restriction of the sheaf
![]() $\omega _E^k[1/p]$
defined in §4.4 over
$\omega _E^k[1/p]$
defined in §4.4 over
![]() $\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
.
$\mathcal {X}_0(p^n,N)_{\infty }^{(m)}$
.
The sheaf
![]() $\mathbf {W}_{k, \mathrm {dR}}$
has a natural, increasing filtration
$\mathbf {W}_{k, \mathrm {dR}}$
has a natural, increasing filtration
![]() $\bigl (\mathrm {Fil}_n\mathbf {W}_{k, \mathrm {dR}} \bigr )_{n\ge 0}$
such that
$\bigl (\mathrm {Fil}_n\mathbf {W}_{k, \mathrm {dR}} \bigr )_{n\ge 0}$
such that
![]() $\omega _E^k[1/p]=\mathrm {Fil}_0\mathbf {W}_{k, \mathrm {dR}}[1/p] $
. The Gauss–Manin connection
$\omega _E^k[1/p]=\mathrm {Fil}_0\mathbf {W}_{k, \mathrm {dR}}[1/p] $
. The Gauss–Manin connection
![]() $\nabla \colon \mathrm {H}_E\to \mathrm {H}_E\otimes \Omega ^{\log }_{\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )/K}$
induces a connection
$\nabla \colon \mathrm {H}_E\to \mathrm {H}_E\otimes \Omega ^{\log }_{\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )/K}$
induces a connection
satisfying Griffiths’ transversality, that is,
![]() $\nabla _k\bigl (\mathrm {Fil}_n\mathbf {W}_{k, \mathrm {dR}}[1/p] \bigr )\subset \mathrm {Fil}_{n+1} \mathbf {W}_{k, \mathrm {dR}}[1/p] \widehat {\otimes } \Omega ^{\log }_{\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )/K}$
.
$\nabla _k\bigl (\mathrm {Fil}_n\mathbf {W}_{k, \mathrm {dR}}[1/p] \bigr )\subset \mathrm {Fil}_{n+1} \mathbf {W}_{k, \mathrm {dR}}[1/p] \widehat {\otimes } \Omega ^{\log }_{\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )/K}$
.
The cohomology groups
![]() $\mathrm {H}^0\bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr ), \mathbf {W}_{k, \mathrm {dR}}\bigr )$
and
$\mathrm {H}^0\bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr ), \mathbf {W}_{k, \mathrm {dR}}\bigr )$
and
![]() $\mathrm {H}^0\bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr ), \mathrm {Fil}_n\mathbf {W}_{k, \mathrm {dR}}\bigr )$
are endowed with an action of the
$\mathrm {H}^0\bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr ), \mathrm {Fil}_n\mathbf {W}_{k, \mathrm {dR}}\bigr )$
are endowed with an action of the
![]() $U_p$
-operator, and for every integer h they admit slope
$U_p$
-operator, and for every integer h they admit slope
![]() $\leq h$
decompositions. Furthermore, we have
$\leq h$
decompositions. Furthermore, we have
![]() $p \nabla _k \circ U_p=U_p \circ \nabla _k$
, and for
$p \nabla _k \circ U_p=U_p \circ \nabla _k$
, and for
![]() $n\gg 0$
we have
$n\gg 0$
we have
Proof. The first statement follows from the fact that the two constructions coincide on
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )_{{\mathbb C}_p}$
. The other statements are proven in [Reference Andreatta and Iovita2]. Namely, the filtration is constructed in Theorem 3.11, the connection in Theorem 3.18, the
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )_{{\mathbb C}_p}$
. The other statements are proven in [Reference Andreatta and Iovita2]. Namely, the filtration is constructed in Theorem 3.11, the connection in Theorem 3.18, the
![]() $U_p$
-operator is defined in §3.6 and the statements about the slope decomposition follow from Correlation 3.26.
$U_p$
-operator is defined in §3.6 and the statements about the slope decomposition follow from Correlation 3.26.
Using the Kodaira–Spencer isomorphism
![]() $\omega _E^2\vert _{\mathcal {X}\big (p/\mathrm {Ha}^{p^s}} \Omega ^{\log }_{\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )/K}$
, we can and will view the connection
$\omega _E^2\vert _{\mathcal {X}\big (p/\mathrm {Ha}^{p^s}} \Omega ^{\log }_{\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )/K}$
, we can and will view the connection
![]() $\nabla _k$
as a map
$\nabla _k$
as a map
![]() $ \nabla _k\colon \mathbf {W}_{k, \mathrm {dR}}[p^{-1}] \to \mathbf {W}_{k+2, \mathrm {dR}}[p^{-1}]$
.
$ \nabla _k\colon \mathbf {W}_{k, \mathrm {dR}}[p^{-1}] \to \mathbf {W}_{k+2, \mathrm {dR}}[p^{-1}]$
.
6.4 The de Rham comparison map
Fix an r-analytic weight
![]() $k\colon {\mathbb Z}_p^{\ast } \to B^{\ast }$
as in definition 3.6. Let
$k\colon {\mathbb Z}_p^{\ast } \to B^{\ast }$
as in definition 3.6. Let
![]() $B_{\mathrm {dR}}^+$
and
$B_{\mathrm {dR}}^+$
and
![]() $B_{\mathrm {dR}}=B_{\mathrm {dR}}^+[t^{-1}]$
be the classical period rings of Fontaine with the canonical topology so that, for example, the quotient topology on
$B_{\mathrm {dR}}=B_{\mathrm {dR}}^+[t^{-1}]$
be the classical period rings of Fontaine with the canonical topology so that, for example, the quotient topology on
![]() $B^+_{\mathrm {dR}}/t B^+_{\mathrm {dR}}={\mathbb C}_p$
is the p-adic topology on
$B^+_{\mathrm {dR}}/t B^+_{\mathrm {dR}}={\mathbb C}_p$
is the p-adic topology on
![]() ${\mathbb C}_p$
. They are endowed with filtrations such that
${\mathbb C}_p$
. They are endowed with filtrations such that
![]() $\mathrm {Fil}^i B_{\mathrm {dR}}=t^i B_{\mathrm {dR}}^+$
for every
$\mathrm {Fil}^i B_{\mathrm {dR}}=t^i B_{\mathrm {dR}}^+$
for every
![]() $i\in {\mathbb Z}$
. We write
$i\in {\mathbb Z}$
. We write
![]() $\mathbf {W}_{k, \mathrm {dR},\bullet }$
for the complex
$\mathbf {W}_{k, \mathrm {dR},\bullet }$
for the complex
![]() $ \mathbf {W}_{k, \mathrm {dR}}[p^{-1}] \to \mathbf {W}_{k+2, \mathrm {dR}}[p^{-1}]$
, where the map is defined by
$ \mathbf {W}_{k, \mathrm {dR}}[p^{-1}] \to \mathbf {W}_{k+2, \mathrm {dR}}[p^{-1}]$
, where the map is defined by
![]() $\nabla _k$
and
$\nabla _k$
and
![]() $\mathrm {Fil}_m \mathbf {W}_{k, \mathrm {dR},\bullet }$
for the subcomplex
$\mathrm {Fil}_m \mathbf {W}_{k, \mathrm {dR},\bullet }$
for the subcomplex
![]() $\mathrm {Fil}_m \mathbf {W}_{k, \mathrm {dR}}[p^{-1}] \to \mathrm {Fil}_{m+1} \mathbf {W}_{k+2, \mathrm {dR}}[p^{-1}]$
. In this section, we use the map
$\mathrm {Fil}_m \mathbf {W}_{k, \mathrm {dR}}[p^{-1}] \to \mathrm {Fil}_{m+1} \mathbf {W}_{k+2, \mathrm {dR}}[p^{-1}]$
. In this section, we use the map
![]() $\alpha _{\mathrm {log}}$
to get the following result.
$\alpha _{\mathrm {log}}$
to get the following result.
Theorem 6.5. We have a Hecke equivariant,
![]() $B\widehat {\otimes } B_{\mathrm {dR}}^+$
-linear,
$B\widehat {\otimes } B_{\mathrm {dR}}^+$
-linear,
![]() $\mathrm {Gal}(\overline {K}/K)$
-equivariant map
$\mathrm {Gal}(\overline {K}/K)$
-equivariant map
where the completed tensor product is taken considering the canonical topology on
![]() $B_{\mathrm {dR}}^+$
. Moreover,
$B_{\mathrm {dR}}^+$
. Moreover,
 $$ \begin{align*} \mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}\bigr)^{(h)}\cong \frac{\mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) ,\mathbf{W}_{k+2, \mathrm{dR}}[1/p]\bigr)^{(h)}}{\nabla_k\left(\mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) ,\mathbf{W}_{k, \mathrm{dR}}[1/p]\bigr)^{ (h-1)}\right)}. \end{align*} $$
$$ \begin{align*} \mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}\bigr)^{(h)}\cong \frac{\mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) ,\mathbf{W}_{k+2, \mathrm{dR}}[1/p]\bigr)^{(h)}}{\nabla_k\left(\mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) ,\mathbf{W}_{k, \mathrm{dR}}[1/p]\bigr)^{ (h-1)}\right)}. \end{align*} $$
Furthermore:
-
i. If
 $u_k (u_k-1) \cdots (u_k-h+1)$
is invertible in
$u_k (u_k-1) \cdots (u_k-h+1)$
is invertible in
 $B[1/p]$
the map
$B[1/p]$
the map
 $\rho _k$
is surjective;
$\rho _k$
is surjective; -
ii. The map
 $\omega _E^{k+2}\to \mathbf {W}_{k+2, \mathrm {dR}}$
induces a surjective map, which is an isomorphism if (i) above holds:
$\omega _E^{k+2}\to \mathbf {W}_{k+2, \mathrm {dR}}$
induces a surjective map, which is an isomorphism if (i) above holds:  $$ \begin{align*} \mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) , \omega^{k+2}_E[1/p]\bigr)^{(h)} \longrightarrow \mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}[1/p]\bigr)^{(h)}. \end{align*} $$
$$ \begin{align*} \mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) , \omega^{k+2}_E[1/p]\bigr)^{(h)} \longrightarrow \mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}[1/p]\bigr)^{(h)}. \end{align*} $$
-
iii. For specializations,
 $B[1/p]\to {\mathbb Q}_p$
so that the composite weight
$B[1/p]\to {\mathbb Q}_p$
so that the composite weight
 $k_0$
is classical,
$k_0$
is classical,
 $\rho _k$
is compatible with the classical de Rham comparison map via the map induced by taking on the left-hand side the pro-Kummer étale cohomology via the projection
$\rho _k$
is compatible with the classical de Rham comparison map via the map induced by taking on the left-hand side the pro-Kummer étale cohomology via the projection $$ \begin{align*} \mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, \mathrm{Sym}^{k_0}(T_p(E)^{\vee})\bigr)\otimes B_{\mathrm{dR}} \cong \mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}, \mathrm{Sym}^{k_0}(\mathrm{H}_E)\bigr) \otimes_{K} B_{\mathrm{dR}} \end{align*} $$
$$ \begin{align*} \mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, \mathrm{Sym}^{k_0}(T_p(E)^{\vee})\bigr)\otimes B_{\mathrm{dR}} \cong \mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}, \mathrm{Sym}^{k_0}(\mathrm{H}_E)\bigr) \otimes_{K} B_{\mathrm{dR}} \end{align*} $$
 ${\mathbb D}_k^o(T_0^{\vee })[n]\to {\mathbb D}_{k_0}^o(T_0^{\vee })[n] \to \mathrm {Sym}^{k_0}(T_p(E)^{\vee })$
and on the right-hand side the restriction map to the open
${\mathbb D}_k^o(T_0^{\vee })[n]\to {\mathbb D}_{k_0}^o(T_0^{\vee })[n] \to \mathrm {Sym}^{k_0}(T_p(E)^{\vee })$
and on the right-hand side the restriction map to the open
 $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
(Here,
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
(Here, $$ \begin{align*} &\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}, \mathrm{Sym}^{k_0}(\mathrm{H}_E)\bigr)\longrightarrow \mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) , \omega^{k_0+2}_E[1/p]\bigr)/\vartheta^{k_0+1}\\ &\quad \times \mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \omega^{-k_0}_E[1/p]\bigr). \end{align*} $$
$$ \begin{align*} &\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}, \mathrm{Sym}^{k_0}(\mathrm{H}_E)\bigr)\longrightarrow \mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) , \omega^{k_0+2}_E[1/p]\bigr)/\vartheta^{k_0+1}\\ &\quad \times \mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \omega^{-k_0}_E[1/p]\bigr). \end{align*} $$
 $\vartheta $
is the classical theta operator on modular forms.)
$\vartheta $
is the classical theta operator on modular forms.)
The proof of Theorem 6.5 will be given in Section §6.4.2.
We now consider the Galois cohomology for the group
![]() $G:=\mathrm {Gal}(\overline {K}/K)$
. Recall that
$G:=\mathrm {Gal}(\overline {K}/K)$
. Recall that
![]() $\mathrm {H}^1\left (G,\mathrm {Fil}^{-1}B_{\mathrm {dR}}(1)\right )=K [\log \chi ]$
, where
$\mathrm {H}^1\left (G,\mathrm {Fil}^{-1}B_{\mathrm {dR}}(1)\right )=K [\log \chi ]$
, where
![]() $\chi $
is the cyclotomic character. More precisely, we see
$\chi $
is the cyclotomic character. More precisely, we see
![]() $\log \chi $
as a
$\log \chi $
as a
![]() $1$
-cocycle
$1$
-cocycle
![]() $\log \chi \colon G\longrightarrow {\mathbb Z}_p\subset \mathrm {Fil}^{-1}B_{\mathrm {dR}}(1)=t(t^{-1}B^+_{\mathrm { dR}})=B^+_{\mathrm {dR}},$
and we denoted
$\log \chi \colon G\longrightarrow {\mathbb Z}_p\subset \mathrm {Fil}^{-1}B_{\mathrm {dR}}(1)=t(t^{-1}B^+_{\mathrm { dR}})=B^+_{\mathrm {dR}},$
and we denoted
![]() $[\log \chi ]$
its cohomology class. We then obtain from Theorem 6.5 the following corollary:
$[\log \chi ]$
its cohomology class. We then obtain from Theorem 6.5 the following corollary:
Corollary 6.6. We have a Hecke equivariant, B-linear map
called the big dual exponential map. It has the property that for every classical weight specialization
![]() $k_0$
it is compatible with the classical dual exponential map as follows:
$k_0$
it is compatible with the classical dual exponential map as follows:
a) If
![]() $k_0>h-1$
, that is,
$k_0>h-1$
, that is,
![]() $k_0$
is a noncritical weight for the slope h, then we have the following commutative diagram with horizontal isomorphisms. Here, we denoted by
$k_0$
is a noncritical weight for the slope h, then we have the following commutative diagram with horizontal isomorphisms. Here, we denoted by
![]() $\exp ^{\ast }_{k_0}$
the Kato dual exponential map associated to weight
$\exp ^{\ast }_{k_0}$
the Kato dual exponential map associated to weight
![]() $k_0$
modular forms.
$k_0$
modular forms.
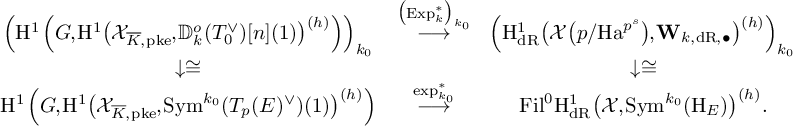 $$ \begin{align*}\begin{array}{ccccccccc} \Bigl(\mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k^o(T_0^{\vee})[n](1) \bigr)^{(h)}\right)\Bigr)_{k_0}&\stackrel{\bigl(\mathrm{Exp}^{\ast}_k\bigr)_{k_0}}{\longrightarrow} &\!\Bigl(\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}\bigr)^{ (h)}\Bigr)_{k_0}\\ \downarrow \cong&&\downarrow\cong\\ \mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, \mathrm{Sym}^{k_0}(T_p(E)^{\vee})(1)\bigr)^{(h)}\right)&\stackrel{\exp^{\ast}_{k_0}}{\longrightarrow} &\mathrm{Fil}^0\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}, \mathrm{Sym}^{k_0}(\mathrm{H}_E)\bigr)^{(h)}. \end{array}\\[-9pt] \end{align*} $$
$$ \begin{align*}\begin{array}{ccccccccc} \Bigl(\mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k^o(T_0^{\vee})[n](1) \bigr)^{(h)}\right)\Bigr)_{k_0}&\stackrel{\bigl(\mathrm{Exp}^{\ast}_k\bigr)_{k_0}}{\longrightarrow} &\!\Bigl(\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}\bigr)^{ (h)}\Bigr)_{k_0}\\ \downarrow \cong&&\downarrow\cong\\ \mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, \mathrm{Sym}^{k_0}(T_p(E)^{\vee})(1)\bigr)^{(h)}\right)&\stackrel{\exp^{\ast}_{k_0}}{\longrightarrow} &\mathrm{Fil}^0\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}, \mathrm{Sym}^{k_0}(\mathrm{H}_E)\bigr)^{(h)}. \end{array}\\[-9pt] \end{align*} $$
b) If
![]() $0\le k_0\le h+1$
, that is,
$0\le k_0\le h+1$
, that is,
![]() $k_0$
is critical with respect to h, we only have a commutative diagram of the form
$k_0$
is critical with respect to h, we only have a commutative diagram of the form
 $$ \begin{align*} \begin{array}{ccccccccc} \Bigl(\mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k^o(T_0^{\vee})[n](1) \bigr)^{(h)}\right)\Bigr)_{k_0}&\stackrel{\bigl(\mathrm{Exp}^{\ast}_k\bigr)_{k_0}}{\longrightarrow} &\!\Bigl(\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}\bigr)^{ (h)}\Bigr)_{k_0}\\ \downarrow &&\uparrow\\ \mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, \mathrm{Sym}^{k_0}(T_p(E)^{\vee})(1)\bigr)^{(h)}\right)&\stackrel{\exp^{\ast}_{k_0}}{\longrightarrow} &\mathrm{Fil}^0\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}, \mathrm{Sym}^{k_0}(\mathrm{H}_E)\bigr)^{(h)}, \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ccccccccc} \Bigl(\mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k^o(T_0^{\vee})[n](1) \bigr)^{(h)}\right)\Bigr)_{k_0}&\stackrel{\bigl(\mathrm{Exp}^{\ast}_k\bigr)_{k_0}}{\longrightarrow} &\!\Bigl(\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}\bigr)^{ (h)}\Bigr)_{k_0}\\ \downarrow &&\uparrow\\ \mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, \mathrm{Sym}^{k_0}(T_p(E)^{\vee})(1)\bigr)^{(h)}\right)&\stackrel{\exp^{\ast}_{k_0}}{\longrightarrow} &\mathrm{Fil}^0\mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}, \mathrm{Sym}^{k_0}(\mathrm{H}_E)\bigr)^{(h)}, \end{array} \end{align*} $$
where the right vertical arrow is induced by restriction.
Proof. Granted Theorem 6.5, we have the following natural B-linear and G-equivariant maps:
whose composition we denote by
![]() $f_k$
. Then we define
$f_k$
. Then we define
![]() $\mathrm {Exp}^{\ast }_k$
as the map induced by composing
$\mathrm {Exp}^{\ast }_k$
as the map induced by composing
![]() $f_k$
in Galois cohomology with the natural isomorphism:
$f_k$
in Galois cohomology with the natural isomorphism:
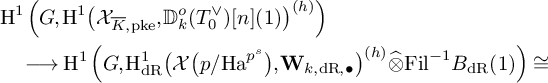 $$ \begin{align*} &\mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k^o(T_0^{\vee})[n](1) \bigr)^{(h)}\right)\\&\quad \longrightarrow \mathrm{H}^1\left(G, \mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}\bigr)^{ (h)}\widehat{\otimes}\mathrm{Fil}^{-1}B_{\mathrm{dR}}(1)\right)\cong \end{align*} $$
$$ \begin{align*} &\mathrm{H}^1\left(G,\mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k^o(T_0^{\vee})[n](1) \bigr)^{(h)}\right)\\&\quad \longrightarrow \mathrm{H}^1\left(G, \mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}\bigr)^{ (h)}\widehat{\otimes}\mathrm{Fil}^{-1}B_{\mathrm{dR}}(1)\right)\cong \end{align*} $$
The vertical maps on the left-hand side of the diagrams in (a) and (b) are induced by the quotient map
![]() ${\mathbb D}_k^o(T_0^{\vee })[n]\vert _{k_0} \to \mathrm { Sym}^{k_0}(T_p(E)^{\vee }$
. The fact that the induced map on the slope
${\mathbb D}_k^o(T_0^{\vee })[n]\vert _{k_0} \to \mathrm { Sym}^{k_0}(T_p(E)^{\vee }$
. The fact that the induced map on the slope
![]() $\leq h$
-part of
$\leq h$
-part of
![]() $\mathrm {H}^1\bigl (\mathcal {X}_{\overline {K},{\mathrm {pke}}}, {\_}\bigr )$
is an isomorphism upon specialization in weight
$\mathrm {H}^1\bigl (\mathcal {X}_{\overline {K},{\mathrm {pke}}}, {\_}\bigr )$
is an isomorphism upon specialization in weight
![]() $k_0$
follows identifying
$k_0$
follows identifying
![]() $\mathrm {H}^1\bigl (\mathcal {X}_{\overline {K},{\mathrm {pke}}},{\_}\bigr )$
with the group cohomology
$\mathrm {H}^1\bigl (\mathcal {X}_{\overline {K},{\mathrm {pke}}},{\_}\bigr )$
with the group cohomology
![]() $ \mathrm {H}^1\bigl (\Gamma _0(p^n)\cap \Gamma (N),{\_}\bigr )$
, arguing as in [Reference Andreatta, Iovita and Stevens5, Prop. 3.18] and using Glenn Stevens’ classicality result of modular symbols; see [Reference Andreatta, Iovita and Stevens5, Thm. 3.16 & Thm. 3.17]. The vertical maps on the right-hand side of the diagrams in (a) and (b) are induced by the inclusion
$ \mathrm {H}^1\bigl (\Gamma _0(p^n)\cap \Gamma (N),{\_}\bigr )$
, arguing as in [Reference Andreatta, Iovita and Stevens5, Prop. 3.18] and using Glenn Stevens’ classicality result of modular symbols; see [Reference Andreatta, Iovita and Stevens5, Thm. 3.16 & Thm. 3.17]. The vertical maps on the right-hand side of the diagrams in (a) and (b) are induced by the inclusion
![]() $ \mathrm {H}^0\bigl (\mathcal {X}, \omega ^{k_0+2}_E\bigr )=\mathrm {Fil}^0\mathrm {H}^1_{\mathrm {dR}}\bigl (\mathcal {X}, \mathrm { Sym}^{k_0}(\mathrm {H}_E)\bigr )\subset \mathrm {H}^1_{\mathrm {dR}}\bigl (\mathcal {X}, \mathrm {Sym}^{k_0}(\mathrm {H}_E)\bigr )$
. The induced map on slope
$ \mathrm {H}^0\bigl (\mathcal {X}, \omega ^{k_0+2}_E\bigr )=\mathrm {Fil}^0\mathrm {H}^1_{\mathrm {dR}}\bigl (\mathcal {X}, \mathrm { Sym}^{k_0}(\mathrm {H}_E)\bigr )\subset \mathrm {H}^1_{\mathrm {dR}}\bigl (\mathcal {X}, \mathrm {Sym}^{k_0}(\mathrm {H}_E)\bigr )$
. The induced map on slope
![]() $\leq h$
-part in (a) is an isomorphism thanks to Theorem 5.1.
$\leq h$
-part in (a) is an isomorphism thanks to Theorem 5.1.
Remark 6.7. The main reason we twist by
![]() $1$
the pro-Kummer étale sheaves
$1$
the pro-Kummer étale sheaves
![]() ${\mathbb D}_k^o(T_0^{\vee })[n]$
and
${\mathbb D}_k^o(T_0^{\vee })[n]$
and
![]() $\mathrm { Sym}^{k_0}\bigl ((T_p(E)^{\vee }\bigr )$
in the corollary above is because the Galois representations attached to overconvergent eigenforms, respectively classical ones are quotients of pro-Kumer étale cohomology of such sheaves (with the twist, that is).
$\mathrm { Sym}^{k_0}\bigl ((T_p(E)^{\vee }\bigr )$
in the corollary above is because the Galois representations attached to overconvergent eigenforms, respectively classical ones are quotients of pro-Kumer étale cohomology of such sheaves (with the twist, that is).
6.4.1 A refinement of the map
 $\alpha _{\mathrm {log}}$
$\alpha _{\mathrm {log}}$
Consider the étale cover
![]() $j_n\colon {{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )\to \mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
given by choosing a generator of
$j_n\colon {{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )\to \mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
given by choosing a generator of
![]() $C_n^{\vee }$
. It is Galois with groups
$C_n^{\vee }$
. It is Galois with groups
![]() $\Delta _n\cong ({\mathbb Z}/p^n{\mathbb Z})^{\ast }$
. Let
$\Delta _n\cong ({\mathbb Z}/p^n{\mathbb Z})^{\ast }$
. Let
![]() $D_n:=(T_p(E)/p^n)/C_n$
. Then we get an exact sequence
$D_n:=(T_p(E)/p^n)/C_n$
. Then we get an exact sequence
![]() $0 \to D_n^{\vee } \to T_p(E)^{\vee }/p^n T_p(E)^{\vee } \to C_n^{\vee } \to 0$
with a marked section s of
$0 \to D_n^{\vee } \to T_p(E)^{\vee }/p^n T_p(E)^{\vee } \to C_n^{\vee } \to 0$
with a marked section s of
![]() $C_n^{\vee }$
.
$C_n^{\vee }$
.
Proposition 6.8. The restriction to
![]() ${{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
of the map
${{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
of the map
![]() $\alpha _{\mathrm {max,n+1}}^{\mathrm {log}}$
factors via the submodule
$\alpha _{\mathrm {max,n+1}}^{\mathrm {log}}$
factors via the submodule
 $\mathrm {H}_E^{\#} \otimes _{{\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+} {\cal O} \mathbb {A}_{\mathrm {max,n+1}}^{\mathrm {log}}\vert _{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}$
. The induced map
$\mathrm {H}_E^{\#} \otimes _{{\cal O}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+} {\cal O} \mathbb {A}_{\mathrm {max,n+1}}^{\mathrm {log}}\vert _{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}$
. The induced map
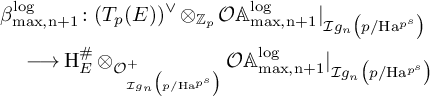 $$ \begin{align*} &\beta_{\mathrm{max,n+1}}^{\mathrm{log}}\colon (T_p (E))^{\vee} \otimes_{{\mathbb Z}_p} {\cal O} \mathbb{A}_{\mathrm{ max,n+1}}^{\mathrm{log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)} \\&\quad \longrightarrow \mathrm{H}_E^{\#} \otimes_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)} \end{align*} $$
$$ \begin{align*} &\beta_{\mathrm{max,n+1}}^{\mathrm{log}}\colon (T_p (E))^{\vee} \otimes_{{\mathbb Z}_p} {\cal O} \mathbb{A}_{\mathrm{ max,n+1}}^{\mathrm{log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)} \\&\quad \longrightarrow \mathrm{H}_E^{\#} \otimes_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)} \end{align*} $$
sends the tautological section P of
![]() $C_n^{\vee }$
to the marked section t of
$C_n^{\vee }$
to the marked section t of
![]() $\mathrm {H}_E^{\#}/p^r \mathrm {H}_E^{\#}$
and sends
$\mathrm {H}_E^{\#}/p^r \mathrm {H}_E^{\#}$
and sends
![]() $D_n^{\vee }$
to
$D_n^{\vee }$
to
![]() $0$
modulo
$0$
modulo
![]() $p^r$
. In particular,
$p^r$
. In particular,
![]() $j_{n,\ast }(\beta _{\mathrm {max,n+1}}^{\mathrm {log}})$
is equivariant for the action of
$j_{n,\ast }(\beta _{\mathrm {max,n+1}}^{\mathrm {log}})$
is equivariant for the action of
![]() $\Delta _n$
.
$\Delta _n$
.
Proof. Let
![]() $\mathcal {J}$
be the kernel of the map
$\mathcal {J}$
be the kernel of the map
![]() ${\cal O} \mathbb {A}_{\mathrm {log}}\to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
. By construction of
${\cal O} \mathbb {A}_{\mathrm {log}}\to \widehat {{\cal O}}_{\mathcal {X}_{{\mathrm {pke}}}}^+$
. By construction of
![]() $\mathbb {A}_{\mathrm {max,n+1}}$
, the ideal
$\mathbb {A}_{\mathrm {max,n+1}}$
, the ideal
![]() $\mathcal {J} $
maps to
$\mathcal {J} $
maps to
![]() $\frac {\mathcal {I}}{p} {\cal O} \mathbb {A}_{\mathrm {max,n+1}}^{\mathrm { log}} \subset p^n {\cal O} \mathbb {A}_{\mathrm {max,n+1}}^{\mathrm {log}}$
via the map
$\frac {\mathcal {I}}{p} {\cal O} \mathbb {A}_{\mathrm {max,n+1}}^{\mathrm { log}} \subset p^n {\cal O} \mathbb {A}_{\mathrm {max,n+1}}^{\mathrm {log}}$
via the map
![]() ${\cal O} \mathbb {A}_{\mathrm {log}} \longrightarrow {\cal O} \mathbb {A}_{\mathrm {max,n+1}}^{\mathrm {log}}$
.
${\cal O} \mathbb {A}_{\mathrm {log}} \longrightarrow {\cal O} \mathbb {A}_{\mathrm {max,n+1}}^{\mathrm {log}}$
.
The map
![]() $\alpha _{\mathrm {log}}$
modulo
$\alpha _{\mathrm {log}}$
modulo
![]() $\mathcal {J}$
coincides with the map
$\mathcal {J}$
coincides with the map
![]() $\mathrm {d log}$
of equation (2) and thanks to Proposition 4.5, its image coincides with
$\mathrm {d log}$
of equation (2) and thanks to Proposition 4.5, its image coincides with
![]() $\omega _E^{\mathrm {mod}} \otimes \widehat {{\cal O}}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+ \subset \mathrm {H}_E^{\#} \otimes \widehat {{\cal O}}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+ \subset \mathrm {H}_E \otimes \widehat {{\cal O}}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
. Also,
$\omega _E^{\mathrm {mod}} \otimes \widehat {{\cal O}}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+ \subset \mathrm {H}_E^{\#} \otimes \widehat {{\cal O}}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+ \subset \mathrm {H}_E \otimes \widehat {{\cal O}}_{{{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
. Also,
![]() $\mathrm {Ha}^p \cdot \mathrm {H}_E\subset \mathrm {H}_E^{\#}$
. As
$\mathrm {Ha}^p \cdot \mathrm {H}_E\subset \mathrm {H}_E^{\#}$
. As
![]() $p/\mathrm {Ha}^p$
is a section of
$p/\mathrm {Ha}^p$
is a section of
![]() ${\cal O}_{ \mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
, we conclude that
${\cal O}_{ \mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )}^+$
, we conclude that
![]() $p \mathrm {H}_E\subset \mathrm {H}_E^{\#}$
. We deduce that the image of
$p \mathrm {H}_E\subset \mathrm {H}_E^{\#}$
. We deduce that the image of
![]() $\alpha _{\mathrm {max,n+1}}^{\mathrm {log}}$
is contained in
$\alpha _{\mathrm {max,n+1}}^{\mathrm {log}}$
is contained in
 $$ \begin{align*} \mathrm{H}_E^{\#} \otimes_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{ log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)} + \mathcal{J} \, \mathrm{H}_E \otimes_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)} \subset\end{align*} $$
$$ \begin{align*} \mathrm{H}_E^{\#} \otimes_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{ log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)} + \mathcal{J} \, \mathrm{H}_E \otimes_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)} \subset\end{align*} $$
 $$ \begin{align*} \subset \!\mathrm{H}_E^{\#} \otimes_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} \!{\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}} \vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\!\bigr)}\! + p\,\mathrm{H}_E \otimes_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+}\! {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)} \subset \end{align*} $$
$$ \begin{align*} \subset \!\mathrm{H}_E^{\#} \otimes_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} \!{\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}} \vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\!\bigr)}\! + p\,\mathrm{H}_E \otimes_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+}\! {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)} \subset \end{align*} $$
 $$ \begin{align*}\subset \mathrm{H}_E^{\#} \otimes_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)} \end{align*} $$
$$ \begin{align*}\subset \mathrm{H}_E^{\#} \otimes_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)} \end{align*} $$
as claimed. We also know that
![]() $\alpha _{\mathrm {log}}$
maps the tautological section P of
$\alpha _{\mathrm {log}}$
maps the tautological section P of
![]() $C_n^{\vee }$
to the marked section t of
$C_n^{\vee }$
to the marked section t of
![]() $\mathrm {H}_E^{\#}/p^r \mathrm {H}_E^{\#}$
modulo
$\mathrm {H}_E^{\#}/p^r \mathrm {H}_E^{\#}$
modulo
![]() $p^r{\cal O} \mathbb {A}_{\mathrm {log}}+ \mathcal {J}$
and sends
$p^r{\cal O} \mathbb {A}_{\mathrm {log}}+ \mathcal {J}$
and sends
![]() $D_n^{\vee }$
to
$D_n^{\vee }$
to
![]() $0$
modulo
$0$
modulo
![]() $p^r {\cal O}\mathbb {A}_{\mathrm {log}}+\mathcal {J}$
. As
$p^r {\cal O}\mathbb {A}_{\mathrm {log}}+\mathcal {J}$
. As
![]() $\mathcal {J}\subset p^n {\cal O} \mathbb {A}_{\mathrm {max,n+1}}$
, the conclusion follows.
$\mathcal {J}\subset p^n {\cal O} \mathbb {A}_{\mathrm {max,n+1}}$
, the conclusion follows.
The equivariance of
![]() $j_{n,\ast }(\beta _{\mathrm {max,n+1}}^{\mathrm {log}})$
follows from the fact that after composing with the inclusion
$j_{n,\ast }(\beta _{\mathrm {max,n+1}}^{\mathrm {log}})$
follows from the fact that after composing with the inclusion
![]() $\mathrm {H}_E^{\#} \subset j_n^{\ast }\bigl (\mathrm {H}_E\bigr )$
, it coincides with
$\mathrm {H}_E^{\#} \subset j_n^{\ast }\bigl (\mathrm {H}_E\bigr )$
, it coincides with
![]() $\alpha _{\mathrm {max,n+1}}^{\mathrm {log}}$
restricted to
$\alpha _{\mathrm {max,n+1}}^{\mathrm {log}}$
restricted to
![]() ${{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
and
${{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
and
![]() $\alpha _{\mathrm {max,n+1}}^{\mathrm {log}}$
is defined over
$\alpha _{\mathrm {max,n+1}}^{\mathrm {log}}$
is defined over
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
.
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
.
Corollary 6.9. Applying the formalism of VBMS to
![]() $\beta _{\mathrm {max,n+1}}^{\mathrm {log}}$
, we get map
$\beta _{\mathrm {max,n+1}}^{\mathrm {log}}$
, we get map
 $$ \begin{align*} &\delta\colon {\mathbb W}_k^D\bigl((T_p(E))^{\vee},D_n^{\vee}, t\bigr)\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)_{\mathrm{pke}}} \\&\quad \longrightarrow \left( \mathbf{W}_{k, \mathrm{dR}} \widehat{\otimes}_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} {\cal O}\mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{ log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}\right)^{\nabla=0} \end{align*} $$
$$ \begin{align*} &\delta\colon {\mathbb W}_k^D\bigl((T_p(E))^{\vee},D_n^{\vee}, t\bigr)\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)_{\mathrm{pke}}} \\&\quad \longrightarrow \left( \mathbf{W}_{k, \mathrm{dR}} \widehat{\otimes}_{{\cal O}_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} {\cal O}\mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{ log}}\vert_{{{\cal I}}g_n\bigl(p/\mathrm{Ha}^{p^s}\bigr)}\right)^{\nabla=0} \end{align*} $$
of sheaves over
![]() ${{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )_{\mathrm {pke}}$
such that
${{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )_{\mathrm {pke}}$
such that
![]() $j_{n,\ast }(\delta )$
is
$j_{n,\ast }(\delta )$
is
![]() $\Delta _n$
-equivariant.
$\Delta _n$
-equivariant.
Composing with the map defined in Corollary 3.9, we get a map of sheaves on
![]() $\mathcal {X} \bigl (p/\mathrm {Ha}^{p^s}\bigr )_{\mathrm {pke}}$
:
$\mathcal {X} \bigl (p/\mathrm {Ha}^{p^s}\bigr )_{\mathrm {pke}}$
:
 $$ \begin{align*} \zeta_k\colon {\mathbb D}_k^o(T_0^{\vee})[n] \longrightarrow \left(\mathbf{W}_{k, \mathrm{dR}} \widehat{\otimes}_{{\cal O}_{\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}[p^{-1}]\right)^{\nabla=0} \end{align*} $$
$$ \begin{align*} \zeta_k\colon {\mathbb D}_k^o(T_0^{\vee})[n] \longrightarrow \left(\mathbf{W}_{k, \mathrm{dR}} \widehat{\otimes}_{{\cal O}_{\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr)}^+} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}[p^{-1}]\right)^{\nabla=0} \end{align*} $$
that is functorial with respect to isogenies
![]() $E\to E'$
inducing an isomorphism on canonical subgroups.
$E\to E'$
inducing an isomorphism on canonical subgroups.
Proof. We define
![]() $\delta $
for a log affinoid perfectoid open W of
$\delta $
for a log affinoid perfectoid open W of
![]() ${{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )_{\mathrm {pke}}$
over an open affinoid
${{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )_{\mathrm {pke}}$
over an open affinoid
![]() $U=\mathrm {Spa}(R,R^+)$
of
$U=\mathrm {Spa}(R,R^+)$
of
![]() ${{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
. We assume that
${{\cal I}}g_n\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
. We assume that
![]() $T_p(E)(W)$
is trivial and that
$T_p(E)(W)$
is trivial and that
![]() $H^{\#}_E(U)$
is a free of rank two
$H^{\#}_E(U)$
is a free of rank two
![]() $R^+$
-module. It is easy to see that we have isomorphisms
$R^+$
-module. It is easy to see that we have isomorphisms
 $$ \begin{align*} &{\mathbb V}_0^D\bigl((T_p(E))^{\vee},D_n^{\vee}, t\bigr) \widehat{\otimes}_{{\mathbb Z}_p} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}(W)\\&\quad \cong {\mathbb V}_0^D\bigl((T_p(E)\otimes_{{\mathbb Z}_p}{\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}(W))^{\vee},D_n^{\vee}\otimes_{\mathbb Z} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}(W), t\bigr) \end{align*} $$
$$ \begin{align*} &{\mathbb V}_0^D\bigl((T_p(E))^{\vee},D_n^{\vee}, t\bigr) \widehat{\otimes}_{{\mathbb Z}_p} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}(W)\\&\quad \cong {\mathbb V}_0^D\bigl((T_p(E)\otimes_{{\mathbb Z}_p}{\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}(W))^{\vee},D_n^{\vee}\otimes_{\mathbb Z} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}(W), t\bigr) \end{align*} $$
and that
Thanks to Proposition 6.8, the map
![]() $\beta _{\mathrm {max,n+1}}^{\mathrm {log}}$
induces a map
$\beta _{\mathrm {max,n+1}}^{\mathrm {log}}$
induces a map
 $$ \begin{align*} &{\mathbb V}_0\bigl(\mathrm{H}_E^{\#}\widehat{\otimes}_{R^+} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}(W), t\bigr)\\ &\quad \to {\mathbb V}_0^D\bigl((T_p(E)\otimes_{{\mathbb Z}_p}{\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}(W))^{\vee},D_n^{\vee}\otimes_{\mathbb Z} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}(W), t\bigr). \end{align*} $$
$$ \begin{align*} &{\mathbb V}_0\bigl(\mathrm{H}_E^{\#}\widehat{\otimes}_{R^+} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}(W), t\bigr)\\ &\quad \to {\mathbb V}_0^D\bigl((T_p(E)\otimes_{{\mathbb Z}_p}{\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}(W))^{\vee},D_n^{\vee}\otimes_{\mathbb Z} {\cal O} \mathbb{A}_{\mathrm{max,n+1}}^{\mathrm{log}}(W), t\bigr). \end{align*} $$
In conclusion, we get a map
This induces the claimed map
![]() $\delta (W)$
. As
$\delta (W)$
. As
![]() $j_{n,\ast }(\beta _{\mathrm {max,n+1}}^{\mathrm {log}})$
is
$j_{n,\ast }(\beta _{\mathrm {max,n+1}}^{\mathrm {log}})$
is
![]() $\Delta _n$
-equivariant due to Proposition 6.8, also
$\Delta _n$
-equivariant due to Proposition 6.8, also
![]() $\delta $
is.
$\delta $
is.
The formalism of VBMS implies that these maps are functorial with respect to isogenies and base change. The connection on
![]() $\mathbf {W}_{k, \mathrm {dR}}$
is defined in [Reference Andreatta and Iovita2] using Grothendieck’s approach: Passing to the base-change over the first infinitesimal neighbourhood of the diagonal of
$\mathbf {W}_{k, \mathrm {dR}}$
is defined in [Reference Andreatta and Iovita2] using Grothendieck’s approach: Passing to the base-change over the first infinitesimal neighbourhood of the diagonal of
![]() $\mathcal {X} \bigl (p/\mathrm {Ha}^{p^s}\bigr )$
, it is realized as an isomorphism between the pullback via the two projections to
$\mathcal {X} \bigl (p/\mathrm {Ha}^{p^s}\bigr )$
, it is realized as an isomorphism between the pullback via the two projections to
![]() $\mathcal {X} \bigl (p/\mathrm {Ha}^{p^s}\bigr )$
using the functoriality of the VBMS formalism. The fact that
$\mathcal {X} \bigl (p/\mathrm {Ha}^{p^s}\bigr )$
using the functoriality of the VBMS formalism. The fact that
![]() $\beta _{\mathrm {max,n+1}}^{\mathrm {log}}$
has image annihilated by
$\beta _{\mathrm {max,n+1}}^{\mathrm {log}}$
has image annihilated by
![]() $\nabla $
implies that the image of
$\nabla $
implies that the image of
![]() $\delta (W)$
is also annihilated by the connection.
$\delta (W)$
is also annihilated by the connection.
Recall that
![]() $\mathrm {H}^1\bigl (\mathcal {X}_{\overline {K},{\mathrm {pke}}}, {\mathbb D}_k^o(T_0^{\vee })[n] \bigr )$
admits slope decompositions for the
$\mathrm {H}^1\bigl (\mathcal {X}_{\overline {K},{\mathrm {pke}}}, {\mathbb D}_k^o(T_0^{\vee })[n] \bigr )$
admits slope decompositions for the
![]() $U_p$
-operator thanks to Proposition 4.13.
$U_p$
-operator thanks to Proposition 4.13.
Lemma 6.10. For every h, there exists m such the map
induced by
![]() $\zeta _k$
, factors via
$\zeta _k$
, factors via
Proof. Consider the complex
![]() $\mathbf {W}_{k, \mathrm {dR},\bullet }/\mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR},\bullet }$
. We claim that for
$\mathbf {W}_{k, \mathrm {dR},\bullet }/\mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR},\bullet }$
. We claim that for
![]() $i=0$
and
$i=0$
and
![]() $1$
$1$
admits a slope h-decomposition and the
![]() $\leq h$
-part is zero, for
$\leq h$
-part is zero, for
![]() $m\gg 0$
. The claim of the lemma then follows upon taking long exact sequences in cohomology associated to the short exact sequences
$m\gg 0$
. The claim of the lemma then follows upon taking long exact sequences in cohomology associated to the short exact sequences
![]() $0\to \mathrm { Fil}_m\mathbf {W}_{k, \mathrm {dR},\bullet } \to \mathbf {W}_{k, \mathrm {dR},\bullet } \to \mathbf {W}_{k, \mathrm {dR},\bullet }/\mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR},\bullet } \to 0$
and using that the slope h-decomposition is an exact operation.
$0\to \mathrm { Fil}_m\mathbf {W}_{k, \mathrm {dR},\bullet } \to \mathbf {W}_{k, \mathrm {dR},\bullet } \to \mathbf {W}_{k, \mathrm {dR},\bullet }/\mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR},\bullet } \to 0$
and using that the slope h-decomposition is an exact operation.
It follows from [Reference Andreatta and Iovita2, Lemma 3.33] that the operator
![]() $U_p$
on
$U_p$
on
is integrally defined and can be written as
![]() $p^{h+1} U^{\prime }_p$
for some operator
$p^{h+1} U^{\prime }_p$
for some operator
![]() $U^{\prime }_p$
for
$U^{\prime }_p$
for
![]() $m\gg 0$
. The proof then follows from [Reference Andreatta, Iovita and Stevens6], Lemma 5.8 and the subsequent claim: One shows that for every polynomial P of slope
$m\gg 0$
. The proof then follows from [Reference Andreatta, Iovita and Stevens6], Lemma 5.8 and the subsequent claim: One shows that for every polynomial P of slope
![]() $\leq h$
,
$\leq h$
,
![]() $P(U_p)$
is invertible on this space after inverting p.
$P(U_p)$
is invertible on this space after inverting p.
6.4.2 Proof of Theorem 6.5
Consider the map
![]() $\mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR},\bullet } \otimes _{{\cal O}_{\mathcal {Y}(p/\mathrm {Ha}^{p^s})}^+} {\cal O}\mathbb {A}_{\mathrm {max,n+1}}[p^{-1}]\to \mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR},\bullet } \otimes _{{\cal O}_{\mathcal {Y}(p/\mathrm {Ha}^{p^s})}^+} \mathrm {Fil}^0 {\cal O}\mathbb {B}_{\mathrm {dR,log}}$
obtained from the morphism
$\mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR},\bullet } \otimes _{{\cal O}_{\mathcal {Y}(p/\mathrm {Ha}^{p^s})}^+} {\cal O}\mathbb {A}_{\mathrm {max,n+1}}[p^{-1}]\to \mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR},\bullet } \otimes _{{\cal O}_{\mathcal {Y}(p/\mathrm {Ha}^{p^s})}^+} \mathrm {Fil}^0 {\cal O}\mathbb {B}_{\mathrm {dR,log}}$
obtained from the morphism
![]() ${\cal O}\mathbb {A}_{\max ,n+1}^{\log }\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
of Lemma 6.2. We recall that the connection
${\cal O}\mathbb {A}_{\max ,n+1}^{\log }\to {\cal O}\mathbb {B}_{\mathrm {dR, log}}^+$
of Lemma 6.2. We recall that the connection
![]() $\nabla ':\mathbf {W}_{k, \mathrm {dR}}\widehat {\otimes }{\cal O}\mathbb {B}_{\mathrm {dR}}\longrightarrow \mathbf {W}_{k+2,\mathrm {dR}}\widehat {\otimes }{\cal O}\mathbb {B}_{\mathrm {dR}}$
has the form
$\nabla ':\mathbf {W}_{k, \mathrm {dR}}\widehat {\otimes }{\cal O}\mathbb {B}_{\mathrm {dR}}\longrightarrow \mathbf {W}_{k+2,\mathrm {dR}}\widehat {\otimes }{\cal O}\mathbb {B}_{\mathrm {dR}}$
has the form
![]() $\nabla '=\nabla _k\widehat {\otimes } 1+1\widehat {\otimes } \nabla _{\mathrm {dR}}$
, where
$\nabla '=\nabla _k\widehat {\otimes } 1+1\widehat {\otimes } \nabla _{\mathrm {dR}}$
, where
![]() $\nabla _k$
is the connection on
$\nabla _k$
is the connection on
![]() $\mathbf {W}_{k, \mathrm {dR}}$
and
$\mathbf {W}_{k, \mathrm {dR}}$
and
![]() $\nabla _{\mathrm {dR}}$
the one on
$\nabla _{\mathrm {dR}}$
the one on
![]() ${\cal O}\mathbb {B}_{\mathrm {dR}}$
. Moreover, both
${\cal O}\mathbb {B}_{\mathrm {dR}}$
. Moreover, both
![]() $\nabla _k$
and
$\nabla _k$
and
![]() $\nabla _{\mathrm {dR}}$
satisfy the Griffith-transversality property with respect to the respective filtrations of
$\nabla _{\mathrm {dR}}$
satisfy the Griffith-transversality property with respect to the respective filtrations of
![]() $\mathbf {W}_{k, \mathrm {dR}}$
and respectively
$\mathbf {W}_{k, \mathrm {dR}}$
and respectively
![]() ${\cal O}\mathbb {B}_{\mathrm {dR}}$
, where let us recall that the first sheaf has an increasing filtration
${\cal O}\mathbb {B}_{\mathrm {dR}}$
, where let us recall that the first sheaf has an increasing filtration
![]() $\mathrm {Fil}_{\bullet }\mathbf {W}_{k, \mathrm {dR}}$
while the second has a decreasing filtration
$\mathrm {Fil}_{\bullet }\mathbf {W}_{k, \mathrm {dR}}$
while the second has a decreasing filtration
![]() $\mathrm {Fil}^{\bullet } {\cal O}\mathbb {B}_{\mathrm {dR}}$
.
$\mathrm {Fil}^{\bullet } {\cal O}\mathbb {B}_{\mathrm {dR}}$
.
For every
![]() $s\ge 1$
, we consider the composition, which we still denote
$s\ge 1$
, we consider the composition, which we still denote
![]() $\nabla '$
:
$\nabla '$
:
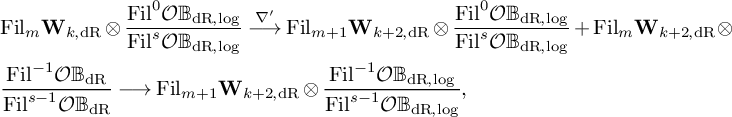 $$ \begin{align*} &\displaystyle \mathrm{Fil}_m\mathbf{W}_{k, \mathrm{dR}} \otimes \frac{ \mathrm{Fil}^0 {\cal O}\mathbb{B}_{\mathrm{dR,log}}}{\mathrm{Fil}^s {\cal O}\mathbb{B}_{\mathrm{dR,log}}}\stackrel{\nabla'}{\longrightarrow} \mathrm{ Fil}_{m+1}\mathbf{W}_{k+2, \mathrm{dR}} \otimes \frac{\mathrm{Fil}^0{\cal O}\mathbb{B}_{\mathrm{dR,log}}}{\mathrm{Fil}^s {\cal O}\mathbb{B}_{\mathrm{dR,log}}}+\mathrm{Fil}_m\mathbf{W}_{k+2,\mathrm{dR}}\otimes \\ &\frac{\mathrm{Fil}^{-1}{\cal O}\mathbb{B}_{\mathrm{dR}}}{\mathrm{Fil}^{s-1}{\cal O}\mathbb{B}_{\mathrm{dR}}}\longrightarrow \mathrm{Fil}_{m+1}\mathbf{W}_{k+2, \mathrm{dR}} \otimes \frac{\mathrm{Fil}^{-1}{\cal O}\mathbb{B}_{\mathrm{dR,log}}}{\mathrm{Fil}^{s-1} {\cal O}\mathbb{B}_{\mathrm{dR,log}}}, \end{align*} $$
$$ \begin{align*} &\displaystyle \mathrm{Fil}_m\mathbf{W}_{k, \mathrm{dR}} \otimes \frac{ \mathrm{Fil}^0 {\cal O}\mathbb{B}_{\mathrm{dR,log}}}{\mathrm{Fil}^s {\cal O}\mathbb{B}_{\mathrm{dR,log}}}\stackrel{\nabla'}{\longrightarrow} \mathrm{ Fil}_{m+1}\mathbf{W}_{k+2, \mathrm{dR}} \otimes \frac{\mathrm{Fil}^0{\cal O}\mathbb{B}_{\mathrm{dR,log}}}{\mathrm{Fil}^s {\cal O}\mathbb{B}_{\mathrm{dR,log}}}+\mathrm{Fil}_m\mathbf{W}_{k+2,\mathrm{dR}}\otimes \\ &\frac{\mathrm{Fil}^{-1}{\cal O}\mathbb{B}_{\mathrm{dR}}}{\mathrm{Fil}^{s-1}{\cal O}\mathbb{B}_{\mathrm{dR}}}\longrightarrow \mathrm{Fil}_{m+1}\mathbf{W}_{k+2, \mathrm{dR}} \otimes \frac{\mathrm{Fil}^{-1}{\cal O}\mathbb{B}_{\mathrm{dR,log}}}{\mathrm{Fil}^{s-1} {\cal O}\mathbb{B}_{\mathrm{dR,log}}}, \end{align*} $$
and we have:
Lemma 6.11. For every
![]() $u\ge 1$
, the natural map of complexes
$u\ge 1$
, the natural map of complexes
 $$ \begin{align*}\begin{array}{cccccccccc} \mathrm{H}^0\Bigl(\mathcal{X}\bigl(\frac{p}{\mathrm{Ha}^{p^rs}}\bigr)_{\overline{K}}, \mathrm{Fil}_m \mathbf{W}_{k, \mathrm{dR}}\Bigr)\widehat{\otimes} \frac{\mathrm{Fil}^0 B_{\mathrm{dR}}}{\mathrm{Fil}^u B_{\mathrm{dR}}} & \stackrel{\nabla}{\longrightarrow} & \mathrm{H}^0\Bigl(\mathcal{X}\bigl(\frac{p}{\mathrm{Ha}^{p^s}}\bigr)_{\overline{K}}, \mathrm{Fil}_{m+1}\mathbf{W}_{k+2, \mathrm{dR}}\Bigr) \\ &&\displaystyle\widehat{\otimes} \frac{ \mathrm{Fil}^{-1} B_{\mathrm{dR}}}{\mathrm{Fil}^{u-1} B_{\mathrm{dR}}}\\\downarrow & & \downarrow \\ \mathrm{H}^0\Bigl(\mathcal{X}\bigl(\frac{p}{\mathrm{Ha}^{p^s}}\bigr)_{\overline{K}}, \mathrm{Fil}_m\mathbf{W}_{k, \mathrm{dR}} \otimes \frac{ \mathrm{Fil}^0 {\cal O}\mathbb{B}_{\mathrm{dR,log}}}{\mathrm{Fil}^u {\cal O}\mathbb{B}_{\mathrm{dR,log}}}\Bigr) & \stackrel{\nabla'}{\longrightarrow}& \mathrm{H}^0\Bigl(\mathcal{X}\bigl(\frac{p}{\mathrm{Ha}^{p^s}}\bigr)_{\overline{K}}, \ \mathrm{Fil}_{m+1}\mathbf{W}_{k+2, \mathrm{dR}}\\ &&\displaystyle\otimes \frac{\mathrm{Fil}^{-1}{\cal O}\mathbb{B}_{\mathrm{dR,log}}}{\mathrm{Fil}^{u-1} {\cal O}\mathbb{B}_{\mathrm{dR,log}}}\Bigr), \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{cccccccccc} \mathrm{H}^0\Bigl(\mathcal{X}\bigl(\frac{p}{\mathrm{Ha}^{p^rs}}\bigr)_{\overline{K}}, \mathrm{Fil}_m \mathbf{W}_{k, \mathrm{dR}}\Bigr)\widehat{\otimes} \frac{\mathrm{Fil}^0 B_{\mathrm{dR}}}{\mathrm{Fil}^u B_{\mathrm{dR}}} & \stackrel{\nabla}{\longrightarrow} & \mathrm{H}^0\Bigl(\mathcal{X}\bigl(\frac{p}{\mathrm{Ha}^{p^s}}\bigr)_{\overline{K}}, \mathrm{Fil}_{m+1}\mathbf{W}_{k+2, \mathrm{dR}}\Bigr) \\ &&\displaystyle\widehat{\otimes} \frac{ \mathrm{Fil}^{-1} B_{\mathrm{dR}}}{\mathrm{Fil}^{u-1} B_{\mathrm{dR}}}\\\downarrow & & \downarrow \\ \mathrm{H}^0\Bigl(\mathcal{X}\bigl(\frac{p}{\mathrm{Ha}^{p^s}}\bigr)_{\overline{K}}, \mathrm{Fil}_m\mathbf{W}_{k, \mathrm{dR}} \otimes \frac{ \mathrm{Fil}^0 {\cal O}\mathbb{B}_{\mathrm{dR,log}}}{\mathrm{Fil}^u {\cal O}\mathbb{B}_{\mathrm{dR,log}}}\Bigr) & \stackrel{\nabla'}{\longrightarrow}& \mathrm{H}^0\Bigl(\mathcal{X}\bigl(\frac{p}{\mathrm{Ha}^{p^s}}\bigr)_{\overline{K}}, \ \mathrm{Fil}_{m+1}\mathbf{W}_{k+2, \mathrm{dR}}\\ &&\displaystyle\otimes \frac{\mathrm{Fil}^{-1}{\cal O}\mathbb{B}_{\mathrm{dR,log}}}{\mathrm{Fil}^{u-1} {\cal O}\mathbb{B}_{\mathrm{dR,log}}}\Bigr), \end{array} \end{align*} $$
where the cohomology is taken with respect to the pro-Kummer étale topology, is an isomorphism.
In the above diagram,
![]() $B_{\mathrm {dR}}$
denotes Fontaine’s classical period ring. Furthermore, this complex represents the cohomology
$B_{\mathrm {dR}}$
denotes Fontaine’s classical period ring. Furthermore, this complex represents the cohomology
![]() $\mathrm {R}\Gamma \bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )_{\overline {K},{\mathrm {pke}}}, \mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR},\bullet } \otimes _{{\cal O}_{\mathcal {X}(p/\mathrm {Ha}^{p^s})}^+} \frac {\mathrm {Fil}^0{\cal O}\mathbb {B}_{\mathrm {dR}}}{\mathrm {Fil}^u {\cal O}\mathbb {B}_{\mathrm {dR}}}\bigr ) $
.
$\mathrm {R}\Gamma \bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )_{\overline {K},{\mathrm {pke}}}, \mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR},\bullet } \otimes _{{\cal O}_{\mathcal {X}(p/\mathrm {Ha}^{p^s})}^+} \frac {\mathrm {Fil}^0{\cal O}\mathbb {B}_{\mathrm {dR}}}{\mathrm {Fil}^u {\cal O}\mathbb {B}_{\mathrm {dR}}}\bigr ) $
.
Proof. Recall that
![]() $ \mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR}}[1/p] $
is a locally free
$ \mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR}}[1/p] $
is a locally free
![]() ${\cal O}_{\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )}$
-module for every m. We prove the result restricting to an affinoid cover
${\cal O}_{\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )}$
-module for every m. We prove the result restricting to an affinoid cover
![]() $\{{\cal U}_i\}_{i\in I}$
, where
$\{{\cal U}_i\}_{i\in I}$
, where
![]() $\mathrm {Fil}_m$
and
$\mathrm {Fil}_m$
and
![]() $\mathrm {Fil}_{m+1}$
are free. Since
$\mathrm {Fil}_{m+1}$
are free. Since
![]() $\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
is affinoid, the Chech complex for
$\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr )$
is affinoid, the Chech complex for
![]() $\mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR}}[1/p]$
w.r.t. the
$\mathrm {Fil}_m\mathbf {W}_{k, \mathrm {dR}}[1/p]$
w.r.t. the
![]() ${\cal U}_i$
’s is exact. As
${\cal U}_i$
’s is exact. As
![]() $\mathrm {Fil}^0 B_{\mathrm {dR}}/\mathrm { Fil}^u B_{\mathrm {dR}}$
is an iterated extension of
$\mathrm {Fil}^0 B_{\mathrm {dR}}/\mathrm { Fil}^u B_{\mathrm {dR}}$
is an iterated extension of
![]() ${\mathbb C}_p$
-vector spaces for every h, the Chech complex remains exact also after taking
${\mathbb C}_p$
-vector spaces for every h, the Chech complex remains exact also after taking
![]() $\widehat {\otimes } \mathrm {Fil}^0 B_{\mathrm {dR}}/\mathrm {Fil}^u B_{\mathrm {dR}}$
. From the result for the
$\widehat {\otimes } \mathrm {Fil}^0 B_{\mathrm {dR}}/\mathrm {Fil}^u B_{\mathrm {dR}}$
. From the result for the
![]() ${\cal U}_i$
’s, we then deduce the lemma.
${\cal U}_i$
’s, we then deduce the lemma.
We are left to show the claim for each
![]() ${\cal U}_i=\mathrm {Spa}(R_i,R_i^+)$
. Then [Reference Diao, Lan, Liu and Zhu16, Lemma 3.3.2] implies that the group
${\cal U}_i=\mathrm {Spa}(R_i,R_i^+)$
. Then [Reference Diao, Lan, Liu and Zhu16, Lemma 3.3.2] implies that the group
![]() $\mathrm {H}^j\bigl ({\cal U}_{i,\overline {K},{\mathrm {pke}}},\mathrm {Fil}^{n}{\cal O}\mathbb {B}_{\mathrm {dR,log}}/\mathrm {Fil}^{n+u} {\cal O}\mathbb {B}_{\mathrm {dR,log}}\bigr )=0$
for
$\mathrm {H}^j\bigl ({\cal U}_{i,\overline {K},{\mathrm {pke}}},\mathrm {Fil}^{n}{\cal O}\mathbb {B}_{\mathrm {dR,log}}/\mathrm {Fil}^{n+u} {\cal O}\mathbb {B}_{\mathrm {dR,log}}\bigr )=0$
for
![]() $j\geq 1$
and coincides with
$j\geq 1$
and coincides with
![]() $\mathrm {Fil}^{n}\left (R_i^+\widehat {\otimes } B_{\mathrm { dR}}\right )/\mathrm {Fil}^{u+n} \left (R_i^+\widehat {\otimes } B_{\mathrm {dR}} \right )$
for
$\mathrm {Fil}^{n}\left (R_i^+\widehat {\otimes } B_{\mathrm { dR}}\right )/\mathrm {Fil}^{u+n} \left (R_i^+\widehat {\otimes } B_{\mathrm {dR}} \right )$
for
![]() $i=0$
, for
$i=0$
, for
![]() $n=0, -1$
. As the latter coincides with
$n=0, -1$
. As the latter coincides with
![]() $R_i^+\widehat {\otimes } \bigl (\mathrm {Fil}^n B_{\mathrm {dR}}/\mathrm {Fil}^{u+n} B_{\mathrm {dR}}\bigr )$
by [Reference Diao, Lan, Liu and Zhu16, Def. 3.1.1], the conclusion follows.
$R_i^+\widehat {\otimes } \bigl (\mathrm {Fil}^n B_{\mathrm {dR}}/\mathrm {Fil}^{u+n} B_{\mathrm {dR}}\bigr )$
by [Reference Diao, Lan, Liu and Zhu16, Def. 3.1.1], the conclusion follows.
We deduce from Lemma 6.10 and Lemma 6.11 that for every positive integer u we have a natural map
 $$ \begin{align*} \mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k^o(T_0^{\vee})[n] \bigr)^{(h)}&\widehat{\otimes} \frac{\mathrm{Fil}^0B_{\mathrm{dR}}}{\mathrm{Fil}^uB_{\mathrm{dR}}}\\&\quad \to\!\frac{ \mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) , \mathrm{Fil}_{m+1} \mathbf{W}_{k+2, \mathrm{dR}}\bigr) \widehat{\otimes} ( \mathrm{Fil}^{-1} B_{\mathrm{dR}}/\mathrm{Fil}^{u-1} B_{\mathrm{dR}}) }{\nabla_k\left( \mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) , \mathrm{Fil}_m \mathbf{W}_{k, \mathrm{dR}}\bigr)\right) \widehat{\otimes} ( \mathrm{Fil}^0 B_{\mathrm{dR}}/\mathrm{Fil}^u B_{\mathrm{dR}})}. \end{align*} $$
$$ \begin{align*} \mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k^o(T_0^{\vee})[n] \bigr)^{(h)}&\widehat{\otimes} \frac{\mathrm{Fil}^0B_{\mathrm{dR}}}{\mathrm{Fil}^uB_{\mathrm{dR}}}\\&\quad \to\!\frac{ \mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) , \mathrm{Fil}_{m+1} \mathbf{W}_{k+2, \mathrm{dR}}\bigr) \widehat{\otimes} ( \mathrm{Fil}^{-1} B_{\mathrm{dR}}/\mathrm{Fil}^{u-1} B_{\mathrm{dR}}) }{\nabla_k\left( \mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) , \mathrm{Fil}_m \mathbf{W}_{k, \mathrm{dR}}\bigr)\right) \widehat{\otimes} ( \mathrm{Fil}^0 B_{\mathrm{dR}}/\mathrm{Fil}^u B_{\mathrm{dR}})}. \end{align*} $$
Recall from Proposition 6.4 that
![]() $\mathrm {H}^0\bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr ) , \mathrm {Fil}_{m} \mathbf {W}_{k, \mathrm {dR}}[1/p]\bigr )$
admits a slope
$\mathrm {H}^0\bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr ) , \mathrm {Fil}_{m} \mathbf {W}_{k, \mathrm {dR}}[1/p]\bigr )$
admits a slope
![]() $\leq {h-1}$
decomposition and
$\leq {h-1}$
decomposition and
![]() $\mathrm {H}^0\bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr ) , \mathrm {Fil}_{m+1} \mathbf {W}_{k+2, \mathrm {dR}}[1/p]\bigr )$
admits a slope
$\mathrm {H}^0\bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr ) , \mathrm {Fil}_{m+1} \mathbf {W}_{k+2, \mathrm {dR}}[1/p]\bigr )$
admits a slope
![]() $\leq h$
decomposition and the slope
$\leq h$
decomposition and the slope
![]() $\leq h-1$
part, resp.
$\leq h-1$
part, resp.
![]() $\leq h$
part, coincides with
$\leq h$
part, coincides with
![]() $\mathrm {H}^0\bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr ) , \mathbf {W}_{k, \mathrm {dR}}[1/p]\bigr )^{(h-1)}$
, resp.
$\mathrm {H}^0\bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr ) , \mathbf {W}_{k, \mathrm {dR}}[1/p]\bigr )^{(h-1)}$
, resp.
![]() $\mathrm {H}^0\bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr ) , \mathbf {W}_{k+2, \mathrm {dR}}[1/p]\bigr )^{(h)}$
.
$\mathrm {H}^0\bigl (\mathcal {X}\bigl (p/\mathrm {Ha}^{p^s}\bigr ) , \mathbf {W}_{k+2, \mathrm {dR}}[1/p]\bigr )^{(h)}$
.
The same then holds after
![]() $\widehat {\otimes }\mathrm {Fil}^0B_{\mathrm {dR}}/\mathrm {Fil}^uB_{\mathrm {dR}}$
, respectively
$\widehat {\otimes }\mathrm {Fil}^0B_{\mathrm {dR}}/\mathrm {Fil}^uB_{\mathrm {dR}}$
, respectively
![]() $\widehat {\otimes } \mathrm {Fil}^{-1}, B_{\mathrm {dR}}/\mathrm {Fil}^{u-1} B_{\mathrm {dR}}$
, and for their quotient via
$\widehat {\otimes } \mathrm {Fil}^{-1}, B_{\mathrm {dR}}/\mathrm {Fil}^{u-1} B_{\mathrm {dR}}$
, and for their quotient via
![]() $\nabla $
(by the five lemma for slope decompositions cf. [Reference Andreatta, Iovita and Stevens6, Thm. 5.7]). As
$\nabla $
(by the five lemma for slope decompositions cf. [Reference Andreatta, Iovita and Stevens6, Thm. 5.7]). As
![]() $\mathrm {Fil}^0B_{\mathrm {dR}}=B_{\mathrm {dR}}^+$
,
$\mathrm {Fil}^0B_{\mathrm {dR}}=B_{\mathrm {dR}}^+$
,
![]() $\mathrm {Fil}^{-1} B_{\mathrm {dR}}=t^{-1}B_{\mathrm {dR}}^+$
and
$\mathrm {Fil}^{-1} B_{\mathrm {dR}}=t^{-1}B_{\mathrm {dR}}^+$
and
![]() $\mathrm {Fil}^{n+u} B_{\mathrm {dR}}=t^{n+u} B_{\mathrm {dR}}^+$
for
$\mathrm {Fil}^{n+u} B_{\mathrm {dR}}=t^{n+u} B_{\mathrm {dR}}^+$
for
![]() $n\in \{-1, 0\}$
, we get maps
$n\in \{-1, 0\}$
, we get maps
 $$ \begin{align*} \mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k^o(T_0^{\vee})[n] \bigr)^{(h)}\widehat{\otimes} \frac{B_{\mathrm{dR}}^+}{t^uB_{\mathrm{dR}}^+}\longrightarrow \mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}[1/p]\bigr)^{(h)}\widehat{\otimes} \frac{ t^{-1}B_{\mathrm{dR}}^+}{t^{u-1} B_{\mathrm{dR}}^+} \end{align*} $$
$$ \begin{align*} \mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k^o(T_0^{\vee})[n] \bigr)^{(h)}\widehat{\otimes} \frac{B_{\mathrm{dR}}^+}{t^uB_{\mathrm{dR}}^+}\longrightarrow \mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}[1/p]\bigr)^{(h)}\widehat{\otimes} \frac{ t^{-1}B_{\mathrm{dR}}^+}{t^{u-1} B_{\mathrm{dR}}^+} \end{align*} $$
with
 $$ \begin{align*} \mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}[1/p]\bigr)^{(h)}\cong \frac{\mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) ,\mathbf{W}_{k+2, \mathrm{dR}}[1/p]\bigr)^{(h)}}{\nabla_k\left(\mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) ,\mathbf{W}_{k, \mathrm{dR}}[1/p]\bigr)^{(h-1)}\right)} \end{align*} $$
$$ \begin{align*} \mathrm{H}^1_{\mathrm{dR}}\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \mathbf{W}_{k, \mathrm{dR},\bullet}[1/p]\bigr)^{(h)}\cong \frac{\mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) ,\mathbf{W}_{k+2, \mathrm{dR}}[1/p]\bigr)^{(h)}}{\nabla_k\left(\mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr) ,\mathbf{W}_{k, \mathrm{dR}}[1/p]\bigr)^{(h-1)}\right)} \end{align*} $$
by [Reference Andreatta and Iovita2, Lemma 3.33 & Eq. (6)]. As they are obtained from maps of sheaves on
![]() $\mathcal {X}_{\mathrm {pke}}$
, the equivariance for the
$\mathcal {X}_{\mathrm {pke}}$
, the equivariance for the
![]() $\mathrm {Gal}(\overline {K}/K)$
-action is clear. The compatibility with Hecke operators follows from the fact that
$\mathrm {Gal}(\overline {K}/K)$
-action is clear. The compatibility with Hecke operators follows from the fact that
![]() $\zeta _k$
is compatible with the map induced by isogenies preserving the canonical subgroup that are used to define the Hecke operators
$\zeta _k$
is compatible with the map induced by isogenies preserving the canonical subgroup that are used to define the Hecke operators
![]() $T_{\ell }$
, for
$T_{\ell }$
, for
![]() $\ell \not \vert pN$
, and the Hecke operator
$\ell \not \vert pN$
, and the Hecke operator
![]() $U_p$
. It is compatible with weight specializations as the map
$U_p$
. It is compatible with weight specializations as the map
![]() $\zeta _k$
is. Taking the inverse limits for
$\zeta _k$
is. Taking the inverse limits for
![]() $u\to \infty $
, we get the statement of Theorem 6.5, except for (i) and (ii). Claim (ii) follows from [Reference Andreatta and Iovita2, section §3.9]. Using (ii), we get a map
$u\to \infty $
, we get the statement of Theorem 6.5, except for (i) and (ii). Claim (ii) follows from [Reference Andreatta and Iovita2, section §3.9]. Using (ii), we get a map
 $$ \begin{align*} \mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k^o(T_0^{\vee})[n] \bigr)^{(h)}\widehat{\otimes} \frac{B_{\mathrm{dR}}^+}{t^uB_{\mathrm{dR}}^+}\longrightarrow \mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \omega_E^k\bigr)^{(h)}\widehat{\otimes} \frac{ t^{-1} B_{\mathrm{dR}}^+}{t^{u-1} B_{\mathrm{dR}}^+}, \end{align*} $$
$$ \begin{align*} \mathrm{H}^1\bigl(\mathcal{X}_{\overline{K},{\mathrm{pke}}}, {\mathbb D}_k^o(T_0^{\vee})[n] \bigr)^{(h)}\widehat{\otimes} \frac{B_{\mathrm{dR}}^+}{t^uB_{\mathrm{dR}}^+}\longrightarrow \mathrm{H}^0\bigl(\mathcal{X}\bigl(p/\mathrm{Ha}^{p^s}\bigr), \omega_E^k\bigr)^{(h)}\widehat{\otimes} \frac{ t^{-1} B_{\mathrm{dR}}^+}{t^{u-1} B_{\mathrm{dR}}^+}, \end{align*} $$
which we’d like to prove is surjective under the hypothesis of i). By devissage it suffices to prove surjectivity for
![]() $u=1$
. As
$u=1$
. As
![]() $t^{-1}B_{\mathrm {dR}}^+/B_{\mathrm {dR}}^+ \cong \mathbb {C}_p(-1)$
, the surjectivity follows from Theorem 5.1.
$t^{-1}B_{\mathrm {dR}}^+/B_{\mathrm {dR}}^+ \cong \mathbb {C}_p(-1)$
, the surjectivity follows from Theorem 5.1.
7 Appendix: Integral slope decomposition
Let us start by formulating the following general property.
We let R be a p-torsion-free
![]() ${\mathbb Z}_p$
-algebra and T an R-module equipped with an R-linear operator
${\mathbb Z}_p$
-algebra and T an R-module equipped with an R-linear operator
![]() $v:T\rightarrow T$
and let
$v:T\rightarrow T$
and let
![]() $\alpha \in R$
be an element such that there is
$\alpha \in R$
be an element such that there is
![]() $r\in {\mathbb N}$
and
$r\in {\mathbb N}$
and
![]() $\gamma \in R$
with
$\gamma \in R$
with
![]() $\alpha \gamma =p^r$
. We denote by
$\alpha \gamma =p^r$
. We denote by
![]() $\rho \colon T\longrightarrow T[1/p]:=T\otimes _RR[1/p]$
and denote by
$\rho \colon T\longrightarrow T[1/p]:=T\otimes _RR[1/p]$
and denote by
![]() $ T^{\mathrm {tors}}:=\mathrm {Ker}(\rho )$
,
$ T^{\mathrm {tors}}:=\mathrm {Ker}(\rho )$
,
![]() $T^{\mathrm {tf}}:=T/T^{\mathrm {tors}}=\mathrm {Im}(\rho )$
and remark that
$T^{\mathrm {tf}}:=T/T^{\mathrm {tors}}=\mathrm {Im}(\rho )$
and remark that
![]() $v-\alpha $
respects the submodule
$v-\alpha $
respects the submodule
![]() $T^{\mathrm {tors}}$
and therefore induces an R-linear map on
$T^{\mathrm {tors}}$
and therefore induces an R-linear map on
![]() $T^{\mathrm {tf}}$
.
$T^{\mathrm {tf}}$
.
Definition 7.1. We say that the triple
![]() $(T,v,\alpha )$
has property
$(T,v,\alpha )$
has property
![]() $(*)$
if
$(*)$
if
-
1) There is
 $w\in {\mathbb N}$
such that
$w\in {\mathbb N}$
such that
 $p^w\bigl (T^{\mathrm {tors}} \bigr )^{v=\alpha }=0.$
$p^w\bigl (T^{\mathrm {tors}} \bigr )^{v=\alpha }=0.$
-
2) There is a
 $\eta \in {\mathbb N}$
, which depends only on
$\eta \in {\mathbb N}$
, which depends only on
 $\alpha $
, such that for every
$\alpha $
, such that for every
 $x\in \bigl (T^{\mathrm {tf}}\bigr )^{v=\alpha } $
there is
$x\in \bigl (T^{\mathrm {tf}}\bigr )^{v=\alpha } $
there is
 $\tilde {x}\in T^{v=\alpha }$
such that
$\tilde {x}\in T^{v=\alpha }$
such that
 $(\tilde {x})^{\mathrm {tf}}=p^{\eta } x$
, where we denoted
$(\tilde {x})^{\mathrm {tf}}=p^{\eta } x$
, where we denoted
 $(\tilde {x})^{\mathrm {tf}}$
the image of
$(\tilde {x})^{\mathrm {tf}}$
the image of
 $\tilde {x}$
in
$\tilde {x}$
in
 $T^{\mathrm {tf}}$
.
$T^{\mathrm {tf}}$
.
The main result of this appendix is the following. Let B denote a ring, and let
![]() $k\colon {\mathbb Z}_p^{\ast }\longrightarrow B^{\ast }$
be a B-valued weight as in Definition 3.6, which is s-analytic. Let
$k\colon {\mathbb Z}_p^{\ast }\longrightarrow B^{\ast }$
be a B-valued weight as in Definition 3.6, which is s-analytic. Let
![]() $\mathcal {X}_{\infty }^{(u)}$
be the adic subspace of the adic modular curve
$\mathcal {X}_{\infty }^{(u)}$
be the adic subspace of the adic modular curve
![]() $\mathcal {X}:=\mathcal {X}_0(p^n,N)$
for
$\mathcal {X}:=\mathcal {X}_0(p^n,N)$
for
![]() $n\geq u$
as in Proposition 4.5. Let
$n\geq u$
as in Proposition 4.5. Let
![]() ${\mathbb D}_k(T_0^{\vee })[n]$
denote the pro-Kummer étale sheaf of weight k distributions, for
${\mathbb D}_k(T_0^{\vee })[n]$
denote the pro-Kummer étale sheaf of weight k distributions, for
![]() $n\geq s$
, over
$n\geq s$
, over
![]() $\mathcal {X}_{\infty }^{(u)}$
and
$\mathcal {X}_{\infty }^{(u)}$
and
![]() $\mathfrak {D}_{k,\infty }^{o,(m)}[n]:={\mathbb D}_k(T_0^{\vee })[n]\widehat {\otimes }{\cal O}_{(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}}^+$
, where we have denoted
$\mathfrak {D}_{k,\infty }^{o,(m)}[n]:={\mathbb D}_k(T_0^{\vee })[n]\widehat {\otimes }{\cal O}_{(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}}^+$
, where we have denoted
![]() ${\cal O}_{(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}}^+$
the structure sheaf of the pro-Kummer étale site of
${\cal O}_{(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}}^+$
the structure sheaf of the pro-Kummer étale site of
![]() $\mathcal {X}_{\infty }^{(u)}$
. We write
$\mathcal {X}_{\infty }^{(u)}$
. We write
![]() $R:={\cal O}^+_{\mathcal {X}_{\infty }^{(u)}}(\mathcal {X}_{\infty }^{(u)})\widehat {\otimes }_{{\mathbb Z}_p}B$
and
$R:={\cal O}^+_{\mathcal {X}_{\infty }^{(u)}}(\mathcal {X}_{\infty }^{(u)})\widehat {\otimes }_{{\mathbb Z}_p}B$
and
![]() $T:=\mathrm {H}^1\bigl ((\mathcal {X}^{(u)}_{\infty } )_{\mathrm {pke}}, \mathfrak {D}_{k,\infty }^{o,(m)}[n]\bigr )$
. On
$T:=\mathrm {H}^1\bigl ((\mathcal {X}^{(u)}_{\infty } )_{\mathrm {pke}}, \mathfrak {D}_{k,\infty }^{o,(m)}[n]\bigr )$
. On
![]() $T[1/p]$
, we have a
$T[1/p]$
, we have a
![]() $B[1/p]$
-linear operator
$B[1/p]$
-linear operator
![]() $U_p$
which has finite slope decompositions by Proposition 4.15.
$U_p$
which has finite slope decompositions by Proposition 4.15.
Let
![]() $Q(X)\in \bigl (B\widehat {\otimes }{\cal O}_{{\mathbb C}_p}\bigr )[X]$
be the polynomial with the property that
$Q(X)\in \bigl (B\widehat {\otimes }{\cal O}_{{\mathbb C}_p}\bigr )[X]$
be the polynomial with the property that
![]() $T[1/p]^{(b)}$
, for some
$T[1/p]^{(b)}$
, for some
![]() $b\in {\mathbb N}$
is the subset of elements
$b\in {\mathbb N}$
is the subset of elements
![]() $x\in T[1/p]$
such that
$x\in T[1/p]$
such that
![]() $Q(U_p)x=0$
. Such a polynomial exists as
$Q(U_p)x=0$
. Such a polynomial exists as
![]() $T[1/p]^{(b)}\cong \mathrm { H}^0\bigl (\mathcal {X}_{\infty }^{(u)}, \omega _E^{k+2} \bigr )[1/p]^{(b)}$
by Proposition 4.15, and on
$T[1/p]^{(b)}\cong \mathrm { H}^0\bigl (\mathcal {X}_{\infty }^{(u)}, \omega _E^{k+2} \bigr )[1/p]^{(b)}$
by Proposition 4.15, and on
![]() $\mathrm { H}^0\bigl (\mathcal {X}_{\infty }^{(u)}, \omega _E^{k+2} \bigr )$
the
$\mathrm { H}^0\bigl (\mathcal {X}_{\infty }^{(u)}, \omega _E^{k+2} \bigr )$
the
![]() $U_p$
operator is compact and has a Fredholm determinant. Then
$U_p$
operator is compact and has a Fredholm determinant. Then
![]() $\alpha :=-Q(0)\in p^a(B\widehat {\otimes }{\cal O}_{{\mathbb C}_p})^{\ast }$
with
$\alpha :=-Q(0)\in p^a(B\widehat {\otimes }{\cal O}_{{\mathbb C}_p})^{\ast }$
with
![]() $a\le b\cdot \mathrm {deg}(Q(X))$
. We write
$a\le b\cdot \mathrm {deg}(Q(X))$
. We write
![]() $Q(X)=P(X)-\alpha $
, with
$Q(X)=P(X)-\alpha $
, with
![]() $P(X)=XR(X)$
and
$P(X)=XR(X)$
and
![]() $P(X), R(X)\in \bigl (B\widehat {\otimes }{\cal O}_{{\mathbb C}_p}\bigr )[X]$
. We denote
$P(X), R(X)\in \bigl (B\widehat {\otimes }{\cal O}_{{\mathbb C}_p}\bigr )[X]$
. We denote
![]() $v:=P(U_p)$
and remark that
$v:=P(U_p)$
and remark that
![]() $x\in T[1/p]^{(b)}$
if and only if
$x\in T[1/p]^{(b)}$
if and only if
![]() $v(x)=\alpha x$
. We have
$v(x)=\alpha x$
. We have
Theorem 7.2. After localizing B to a new p-adically complete ring which we denote by
![]() $B'$
and replacing R by
$B'$
and replacing R by
![]() $R':={\cal O}^+_{\mathcal {X}_{\infty }^{(u)}}(\mathcal {X}_{\infty }^{(u)})\widehat {\otimes }_{{\mathbb Z}_p}B'$
and T by
$R':={\cal O}^+_{\mathcal {X}_{\infty }^{(u)}}(\mathcal {X}_{\infty }^{(u)})\widehat {\otimes }_{{\mathbb Z}_p}B'$
and T by
![]() $T':=T\otimes _RR'$
the triple
$T':=T\otimes _RR'$
the triple
![]() $(T',v\otimes 1_{R'},\alpha )$
above satisfies property
$(T',v\otimes 1_{R'},\alpha )$
above satisfies property
![]() $(\ast )$
of definition 7.1.
$(\ast )$
of definition 7.1.
Before we start on the proof of this theorem, we need a few lemmas. We remind the reader that the sheaf
![]() $\mathfrak {D}_{k,\infty }^{o,(m)}[n] $
has a decreasing filtration
$\mathfrak {D}_{k,\infty }^{o,(m)}[n] $
has a decreasing filtration
![]() $\bigl ({\mathfrak {Fil}}^{\nu }\bigr )_{\nu \ge 0}$
by subsheaves with the property (see Proposition 4.15): For all
$\bigl ({\mathfrak {Fil}}^{\nu }\bigr )_{\nu \ge 0}$
by subsheaves with the property (see Proposition 4.15): For all
![]() $\nu \ge 0$
and
$\nu \ge 0$
and
![]() $i\ge 0$
we have
$i\ge 0$
we have
Moreover, we have
![]() ${\mathfrak {Fil}}^{\nu }/{\mathfrak {Fil}}^{\nu +1}\cong \omega _E^{k-2\nu -2}\widehat {\otimes }{\cal O}_{\mathcal {X}_{\infty }^{(u)}}(\nu +1)$
by equation (5). With these notations we have:
${\mathfrak {Fil}}^{\nu }/{\mathfrak {Fil}}^{\nu +1}\cong \omega _E^{k-2\nu -2}\widehat {\otimes }{\cal O}_{\mathcal {X}_{\infty }^{(u)}}(\nu +1)$
by equation (5). With these notations we have:
Lemma 7.3. For every
![]() $\nu \in {\mathbb N}$
large enough and
$\nu \in {\mathbb N}$
large enough and
![]() $i\ge 0$
the triple
$i\ge 0$
the triple
![]() $\Bigl (T_i^{\nu }:=\mathrm {H}^i\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {Fil}}^{\nu }\bigr ), v=P(U_p), \alpha \Bigr )$
satisfies property
$\Bigl (T_i^{\nu }:=\mathrm {H}^i\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {Fil}}^{\nu }\bigr ), v=P(U_p), \alpha \Bigr )$
satisfies property
![]() $(\ast )$
of definition 7.1.
$(\ast )$
of definition 7.1.
Proof. We have the following commutative diagram with exact rows:
 $$ \begin{align*}\begin{array}{llllllllllll} 0&\longrightarrow&\bigl(T_i^{\nu}\bigr)^{\mathrm{tors}}&\longrightarrow & T_i^{\nu} &\longrightarrow &\bigl(T_i^{\nu} \bigr)^{\mathrm{, tf}} &\longrightarrow &0\\ & &\downarrow v-\alpha & &\downarrow v-\alpha & &\downarrow v-\alpha\\ 0 &\longrightarrow &\bigl(T_i^{\nu}\bigr)^{\mathrm{tors}} &\longrightarrow &T_i^{\nu} &\longrightarrow &\bigl(T_i^{\nu} \bigr)^{\mathrm{, tf}} &\longrightarrow &0. \\ \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{llllllllllll} 0&\longrightarrow&\bigl(T_i^{\nu}\bigr)^{\mathrm{tors}}&\longrightarrow & T_i^{\nu} &\longrightarrow &\bigl(T_i^{\nu} \bigr)^{\mathrm{, tf}} &\longrightarrow &0\\ & &\downarrow v-\alpha & &\downarrow v-\alpha & &\downarrow v-\alpha\\ 0 &\longrightarrow &\bigl(T_i^{\nu}\bigr)^{\mathrm{tors}} &\longrightarrow &T_i^{\nu} &\longrightarrow &\bigl(T_i^{\nu} \bigr)^{\mathrm{, tf}} &\longrightarrow &0. \\ \end{array} \end{align*} $$
We remark that the above property about the behavior of
![]() $U_p$
with respect to the cohomology of the filtration and the fact that v is the composition of
$U_p$
with respect to the cohomology of the filtration and the fact that v is the composition of
![]() $U_p$
, with an endomorphism of
$U_p$
, with an endomorphism of
![]() $T_i^{\nu }$
which commutes with
$T_i^{\nu }$
which commutes with
![]() $U_p$
, implies that there is
$U_p$
, implies that there is
![]() $\nu _0$
such that for all
$\nu _0$
such that for all
![]() $\nu \ge \nu _0$
we have
$\nu \ge \nu _0$
we have
![]() $(v-\alpha \cdot \mathrm {Id}_{T^{\nu }_i})=\alpha U^{\prime }_i$
, where
$(v-\alpha \cdot \mathrm {Id}_{T^{\nu }_i})=\alpha U^{\prime }_i$
, where
![]() $U^{\prime }_i:T^{\nu }_i\longrightarrow T^{\nu }_i$
is an isomorphism. Therefore,
$U^{\prime }_i:T^{\nu }_i\longrightarrow T^{\nu }_i$
is an isomorphism. Therefore,
![]() $\bigl (T_i^{\nu })\bigr )^{v=\alpha }=T^{\nu }_i[\alpha ]=\bigl (T^{\nu }_i\bigr )^{\mathrm {tors}}[\alpha ]$
and
$\bigl (T_i^{\nu })\bigr )^{v=\alpha }=T^{\nu }_i[\alpha ]=\bigl (T^{\nu }_i\bigr )^{\mathrm {tors}}[\alpha ]$
and
![]() $\bigl (T^{\nu }_i\bigr )^{\mathrm {tf}}[\alpha ]=0$
. Therefore, 1) of property
$\bigl (T^{\nu }_i\bigr )^{\mathrm {tf}}[\alpha ]=0$
. Therefore, 1) of property
![]() $(*)$
follows:
$(*)$
follows:
![]() $\alpha \Bigl (\bigl (T^{\nu }_i\bigr )^{\mathrm {tors}}\Bigr )^{v=\alpha }= \alpha (T^{\nu }_i[\alpha ])=0$
. For property 2), let
$\alpha \Bigl (\bigl (T^{\nu }_i\bigr )^{\mathrm {tors}}\Bigr )^{v=\alpha }= \alpha (T^{\nu }_i[\alpha ])=0$
. For property 2), let
![]() $x\in \Bigl (\bigl (T^{\nu }_i \bigr )^{\mathrm {tf}}\Bigr )^{v=\alpha }=0$
. For every
$x\in \Bigl (\bigl (T^{\nu }_i \bigr )^{\mathrm {tf}}\Bigr )^{v=\alpha }=0$
. For every
![]() $y\in \bigl (T^{\nu }_i\bigr )^{v=\alpha }=T^{\nu }_i[\alpha ]$
, we have
$y\in \bigl (T^{\nu }_i\bigr )^{v=\alpha }=T^{\nu }_i[\alpha ]$
, we have
![]() $\alpha y=0=x$
.
$\alpha y=0=x$
.
Lemma 7.4. For every
![]() $\nu \in {\mathbb N}$
, the triple
$\nu \in {\mathbb N}$
, the triple
![]() $\Bigl (T_{\nu }:=\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o/{\mathfrak {Fil}}^{\nu }\bigr ), u= P(U_p), \alpha \Bigr )$
satisfies the property
$\Bigl (T_{\nu }:=\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {D}}_k^o/{\mathfrak {Fil}}^{\nu }\bigr ), u= P(U_p), \alpha \Bigr )$
satisfies the property
![]() $(\ast )$
of Definition 7.1.
$(\ast )$
of Definition 7.1.
Proof. In order to prove the lemma, we’ll use induction on
![]() $\nu \ge 0$
. For
$\nu \ge 0$
. For
![]() $\nu =0$
, we have
$\nu =0$
, we have
![]() ${\mathfrak {D}}_k/{\mathfrak {Fil}}^0\cong \omega _E^k\widehat {\otimes }{\cal O}^+_{\mathcal {X}_{\infty }^{(u)}}$
; therefore, we have:
${\mathfrak {D}}_k/{\mathfrak {Fil}}^0\cong \omega _E^k\widehat {\otimes }{\cal O}^+_{\mathcal {X}_{\infty }^{(u)}}$
; therefore, we have:
1)
![]() $p^{1/(p-1)}(T_0)^{\mathrm {tors}}=p^{1/(p-1)}\mathrm {H}^1\bigl ( (\mathcal {X}^{(u)}_{\infty })_{\mathrm {pke}}, \widehat {{\cal O}}^+_{\mathcal {X}_{\infty }^{(u)}}\bigr )^{\mathrm {tors}}\widehat {\otimes }\mathrm { H}^0(\mathcal {X}_{\infty }^{(u)}, \omega _E^k)=0$
as computed by Faltings; see [Reference Scholze22, Lemma 5.5 & 5.6] when the log structure is trivial and their analogues [Reference Diao, Lan, Liu and Zhu15, Lemma 6.1.7 & 6.1.11] in the general case;
$p^{1/(p-1)}(T_0)^{\mathrm {tors}}=p^{1/(p-1)}\mathrm {H}^1\bigl ( (\mathcal {X}^{(u)}_{\infty })_{\mathrm {pke}}, \widehat {{\cal O}}^+_{\mathcal {X}_{\infty }^{(u)}}\bigr )^{\mathrm {tors}}\widehat {\otimes }\mathrm { H}^0(\mathcal {X}_{\infty }^{(u)}, \omega _E^k)=0$
as computed by Faltings; see [Reference Scholze22, Lemma 5.5 & 5.6] when the log structure is trivial and their analogues [Reference Diao, Lan, Liu and Zhu15, Lemma 6.1.7 & 6.1.11] in the general case;
and
2) If
![]() $x\in (T_0)^{\mathrm {tf}}$
is such that
$x\in (T_0)^{\mathrm {tf}}$
is such that
![]() $(v-\alpha )x=0$
, let
$(v-\alpha )x=0$
, let
![]() $y\in T_0$
be any lift of x. Then
$y\in T_0$
be any lift of x. Then
![]() $(v-\alpha )(y)\in T_0^{\mathrm {tors}}$
; therefore,
$(v-\alpha )(y)\in T_0^{\mathrm {tors}}$
; therefore,
![]() $z:=p^{1/(p-1)}y\in T_0$
satisfies:
$z:=p^{1/(p-1)}y\in T_0$
satisfies:
![]() $(v-\alpha )(z)=0$
and
$(v-\alpha )(z)=0$
and
![]() $z^{\mathrm {tf}}=p^{1/(p-1)}x$
, where we wrote
$z^{\mathrm {tf}}=p^{1/(p-1)}x$
, where we wrote
![]() $z^{\mathrm {tf}}$
for the image of z in
$z^{\mathrm {tf}}$
for the image of z in
![]() $T_0^{\mathrm {tf}}$
. Let us observe that we proved more then 1) of property
$T_0^{\mathrm {tf}}$
. Let us observe that we proved more then 1) of property
![]() $(\ast )$
; namely, we showed that there is
$(\ast )$
; namely, we showed that there is
![]() $r\ge 0$
such that
$r\ge 0$
such that
![]() $p^rT_0^{\mathrm {tors}}=0$
. We’ll prove the same property, call it
$p^rT_0^{\mathrm {tors}}=0$
. We’ll prove the same property, call it
![]() $(\ast \ast )$
for all
$(\ast \ast )$
for all
![]() $\nu \ge 0$
.
$\nu \ge 0$
.
Suppose now that
![]() $(\ast \ast )$
is true for
$(\ast \ast )$
is true for
![]() $T_{\nu }$
,
$T_{\nu }$
,
![]() $\nu \ge 1$
, and let us prove it for
$\nu \ge 1$
, and let us prove it for
![]() $T_{\nu +1}$
. We have an exact sequence of pro-Kumer étale sheaves on the site
$T_{\nu +1}$
. We have an exact sequence of pro-Kumer étale sheaves on the site
![]() ${\cal V}:=(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}$
:
${\cal V}:=(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}$
:
therefore a long exact cohomology sequence:
 $$ \begin{align*}{\cal A}&:=\mathrm{H}^0({\cal V}, {\mathfrak{D}}_k/{\mathfrak{Fil}}^{\nu})\stackrel{\beta}{\rightarrow}\mathcal{B}:=\mathrm{H}^1({\cal V}, {\mathfrak{Fil}}^{\nu}/{\mathfrak{Fil}}^{\nu+1})\stackrel{\gamma}{\rightarrow}\\{\cal C}&:=\mathrm{H}^1({\cal V}, {\mathfrak{D}}/{\mathfrak{Fil}}^{\nu+1})\stackrel{\delta}{\rightarrow}{\cal D}:=\mathrm{H}^1({\cal V}, {\mathfrak{D}}/{\mathfrak{Fil}}^{\nu})\rightarrow 0. \end{align*} $$
$$ \begin{align*}{\cal A}&:=\mathrm{H}^0({\cal V}, {\mathfrak{D}}_k/{\mathfrak{Fil}}^{\nu})\stackrel{\beta}{\rightarrow}\mathcal{B}:=\mathrm{H}^1({\cal V}, {\mathfrak{Fil}}^{\nu}/{\mathfrak{Fil}}^{\nu+1})\stackrel{\gamma}{\rightarrow}\\{\cal C}&:=\mathrm{H}^1({\cal V}, {\mathfrak{D}}/{\mathfrak{Fil}}^{\nu+1})\stackrel{\delta}{\rightarrow}{\cal D}:=\mathrm{H}^1({\cal V}, {\mathfrak{D}}/{\mathfrak{Fil}}^{\nu})\rightarrow 0. \end{align*} $$
By the induction hypothesis, there is r such that
![]() $p^r{\cal A}^{\mathrm {tors}}=p^r\mathcal {B}^{\mathrm {tors}}=p^r{\cal D}^{\mathrm {tors}}=0$
. We have the commutative diagram with the middle row exact:
$p^r{\cal A}^{\mathrm {tors}}=p^r\mathcal {B}^{\mathrm {tors}}=p^r{\cal D}^{\mathrm {tors}}=0$
. We have the commutative diagram with the middle row exact:
 $$ \begin{align*}\begin{array}{cccccccccccccc} &{\cal A}^{\mathrm{tors}}&\stackrel{\beta}{\longrightarrow}&\mathcal{B}^{\mathrm{tors}}&\stackrel{\gamma}{\longrightarrow}&{\cal C}^{\mathrm{tors}}&\stackrel{\delta}{\longrightarrow}&{\cal D}^{\mathrm{tors}}\\ &\downarrow&&\downarrow&&\downarrow&&\downarrow\\ (1)\quad& {\cal A}&\stackrel{\beta}{\longrightarrow}&\mathcal{B}&\stackrel{\gamma}{\longrightarrow}&{\cal C}&\stackrel{\delta}{\longrightarrow}&{\cal D}&\longrightarrow 0\\ &\downarrow&&\downarrow&&\downarrow&&\downarrow\\ &{\cal A}^{\mathrm{tf}}&\stackrel{\beta}{\longrightarrow}&\mathcal{B}^{\mathrm{tf}}&\stackrel{\gamma}{\longrightarrow}&{\cal C}^{\mathrm{tf}}&\stackrel{\delta}{\longrightarrow}&{\cal D}^{\mathrm{tf}}. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{cccccccccccccc} &{\cal A}^{\mathrm{tors}}&\stackrel{\beta}{\longrightarrow}&\mathcal{B}^{\mathrm{tors}}&\stackrel{\gamma}{\longrightarrow}&{\cal C}^{\mathrm{tors}}&\stackrel{\delta}{\longrightarrow}&{\cal D}^{\mathrm{tors}}\\ &\downarrow&&\downarrow&&\downarrow&&\downarrow\\ (1)\quad& {\cal A}&\stackrel{\beta}{\longrightarrow}&\mathcal{B}&\stackrel{\gamma}{\longrightarrow}&{\cal C}&\stackrel{\delta}{\longrightarrow}&{\cal D}&\longrightarrow 0\\ &\downarrow&&\downarrow&&\downarrow&&\downarrow\\ &{\cal A}^{\mathrm{tf}}&\stackrel{\beta}{\longrightarrow}&\mathcal{B}^{\mathrm{tf}}&\stackrel{\gamma}{\longrightarrow}&{\cal C}^{\mathrm{tf}}&\stackrel{\delta}{\longrightarrow}&{\cal D}^{\mathrm{tf}}. \end{array} \end{align*} $$
Let us suppose that there is
![]() $s\ge 0$
such that
$s\ge 0$
such that
![]() $p^s\Bigl (\mathcal {B}^{\mathrm {tf}}/\beta ({\cal A}^{\mathrm {tf}}) \Bigr )^{\mathrm {tors}}=0$
. Then we claim that
$p^s\Bigl (\mathcal {B}^{\mathrm {tf}}/\beta ({\cal A}^{\mathrm {tf}}) \Bigr )^{\mathrm {tors}}=0$
. Then we claim that
![]() $p^{2r+s}{\cal C}^{\mathrm {tors}}=0$
. To see it, let
$p^{2r+s}{\cal C}^{\mathrm {tors}}=0$
. To see it, let
![]() $c\in {\cal C}^{\mathrm {tors}}$
, then
$c\in {\cal C}^{\mathrm {tors}}$
, then
![]() $p^rx=\gamma (y)$
,
$p^rx=\gamma (y)$
,
![]() $y\in B$
. We denote by
$y\in B$
. We denote by
![]() $[y]$
the image of y in
$[y]$
the image of y in
![]() $\mathcal {B}^{\mathrm {tf}}/\beta ({\cal A}^{\mathrm {tf}})$
. As
$\mathcal {B}^{\mathrm {tf}}/\beta ({\cal A}^{\mathrm {tf}})$
. As
![]() $p^Nx=0$
for some
$p^Nx=0$
for some
![]() $N\ge 0$
we have that
$N\ge 0$
we have that
![]() $p^N[y]=0$
, therefore
$p^N[y]=0$
, therefore
![]() $[y]\in \Big (\mathcal {B}^{\mathrm {tf}}/\beta ({\cal A}^{\mathrm {tf}} \Big )^{\mathrm {tors}}$
and so by the above assumption
$[y]\in \Big (\mathcal {B}^{\mathrm {tf}}/\beta ({\cal A}^{\mathrm {tf}} \Big )^{\mathrm {tors}}$
and so by the above assumption
![]() $p^s[y]=0$
. Let
$p^s[y]=0$
. Let
![]() $z\in {\cal A}$
be such that
$z\in {\cal A}$
be such that
![]() $\beta (z^{\mathrm {tf}})=p^sy^{\mathrm {tf}}$
in
$\beta (z^{\mathrm {tf}})=p^sy^{\mathrm {tf}}$
in
![]() $\mathcal {B}^{\mathrm {tf}}$
. It follows that
$\mathcal {B}^{\mathrm {tf}}$
. It follows that
![]() $\beta (z)-p^sy\in \mathcal {B}^{\mathrm {tors}}$
which implies that
$\beta (z)-p^sy\in \mathcal {B}^{\mathrm {tors}}$
which implies that
![]() $p^{r+s}y=p^r\beta (z)$
. Therefore,
$p^{r+s}y=p^r\beta (z)$
. Therefore,
![]() $p^{s+2r}x=0$
.
$p^{s+2r}x=0$
.
Let us now prove the remaining claim, namely that there is
![]() $s\ge 0$
such that
$s\ge 0$
such that
![]() $p^s\Big (\mathcal {B}^{\mathrm {tf}}/\beta ({\cal A}^{\mathrm {tf}} \Big )^{\mathrm {tors}}=0$
. For this, let us recall [Reference Andreatta, Iovita and Stevens6] that we have a commutative diagram with exact rows
$p^s\Big (\mathcal {B}^{\mathrm {tf}}/\beta ({\cal A}^{\mathrm {tf}} \Big )^{\mathrm {tors}}=0$
. For this, let us recall [Reference Andreatta, Iovita and Stevens6] that we have a commutative diagram with exact rows
 $$ \begin{align*}\begin{array}{ccccccccccc} && \mathrm{H}^0(\mathcal{X}_{\infty}^{(u)}, \omega^{k-2\nu}_E)&\stackrel{\tilde{\beta}}{\longrightarrow}&\mathrm{H}^0(\mathcal{X}_{\infty}^{(u)}, \omega_E^{k-2\nu})&\longrightarrow&\mathrm{Coker}(\tilde{\beta})&\longrightarrow&0\\ &&\downarrow i&&\downarrow j&&\downarrow u\\ &&A^{\mathrm{tf}}&\stackrel{\beta}{\longrightarrow}&\mathcal{B}^{\mathrm{tf}}&\longrightarrow&\mathcal{B}^{\mathrm{tf}}/\beta({\cal A}^{\mathrm{tf}})&\longrightarrow&0, \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccccccccccc} && \mathrm{H}^0(\mathcal{X}_{\infty}^{(u)}, \omega^{k-2\nu}_E)&\stackrel{\tilde{\beta}}{\longrightarrow}&\mathrm{H}^0(\mathcal{X}_{\infty}^{(u)}, \omega_E^{k-2\nu})&\longrightarrow&\mathrm{Coker}(\tilde{\beta})&\longrightarrow&0\\ &&\downarrow i&&\downarrow j&&\downarrow u\\ &&A^{\mathrm{tf}}&\stackrel{\beta}{\longrightarrow}&\mathcal{B}^{\mathrm{tf}}&\longrightarrow&\mathcal{B}^{\mathrm{tf}}/\beta({\cal A}^{\mathrm{tf}})&\longrightarrow&0, \end{array} \end{align*} $$
where i and j are injective with cokernels killed by
![]() $p^{\nu /(p-1)}$
and
$p^{\nu /(p-1)}$
and
![]() $p^{1/(p-1)}$
, respectively. Moreover, it follows using the explicit basis of the filtration described in Proposition 4.14 and [Reference Andreatta, Iovita and Stevens6, Prop. 5.2] that
$p^{1/(p-1)}$
, respectively. Moreover, it follows using the explicit basis of the filtration described in Proposition 4.14 and [Reference Andreatta, Iovita and Stevens6, Prop. 5.2] that
![]() $\tilde {\beta }=\bigl (\prod _{n=0}^{\nu } (u_k-n)\bigr )\beta '$
, with
$\tilde {\beta }=\bigl (\prod _{n=0}^{\nu } (u_k-n)\bigr )\beta '$
, with
![]() $\beta '$
an isomorphism. As
$\beta '$
an isomorphism. As
![]() $p^{1/(p-1)}$
kills
$p^{1/(p-1)}$
kills
![]() $\mathrm {Coker}(j)$
, it also kills
$\mathrm {Coker}(j)$
, it also kills
![]() $\mathrm {Coker}(u)$
. Therefore, it is enough to prove the claim for
$\mathrm {Coker}(u)$
. Therefore, it is enough to prove the claim for
![]() $\mathrm {Coker}(\tilde {\beta })^{\mathrm {tors}}$
. We have two possibilities. Either
$\mathrm {Coker}(\tilde {\beta })^{\mathrm {tors}}$
. We have two possibilities. Either
![]() $u_k=n$
for some
$u_k=n$
for some
![]() $0\leq n\leq \nu $
and then
$0\leq n\leq \nu $
and then
![]() $\mathcal {B}^{\mathrm { tf}}/\beta ({\cal A}^{\mathrm {tf}})=\mathcal {B}^{\mathrm {tf}}$
so that the claim is obvious. Else
$\mathcal {B}^{\mathrm { tf}}/\beta ({\cal A}^{\mathrm {tf}})=\mathcal {B}^{\mathrm {tf}}$
so that the claim is obvious. Else
![]() $\prod _{n=0}^{\nu } (u_k-n)\in (B[1/p])^{\ast }$
due to our assumption on B in Definition 3.6, that is, there exists
$\prod _{n=0}^{\nu } (u_k-n)\in (B[1/p])^{\ast }$
due to our assumption on B in Definition 3.6, that is, there exists
![]() $s\in {\mathbb N}$
and
$s\in {\mathbb N}$
and
![]() $v\in B$
such that
$v\in B$
such that
![]() $ \prod _{n=0}^{\nu } (u_k-n) \cdot v=p^s$
. Then
$ \prod _{n=0}^{\nu } (u_k-n) \cdot v=p^s$
. Then
![]() $ \tilde {\beta }$
is injective with the cokernel annihilated by
$ \tilde {\beta }$
is injective with the cokernel annihilated by
![]() $p^s$
and the claim is proven also in this case.
$p^s$
and the claim is proven also in this case.
So we have proved that the property
![]() $(\ast \ast )$
holds for triples
$(\ast \ast )$
holds for triples
![]() $(T_{\nu }, v=P(U_p), \alpha )$
for all
$(T_{\nu }, v=P(U_p), \alpha )$
for all
![]() $\nu \ge 0$
, which implies 1) of property
$\nu \ge 0$
, which implies 1) of property
![]() $(\ast )$
.
$(\ast )$
.
Let us prove 2) of property
![]() $(\ast )$
for
$(\ast )$
for
![]() ${\cal C}$
, supposing that it holds for
${\cal C}$
, supposing that it holds for
![]() ${\cal D}$
. We recall our diagram
${\cal D}$
. We recall our diagram
![]() $(1)$
and let
$(1)$
and let
![]() $x\in {\cal C}^{\mathrm {tf}}$
be such that
$x\in {\cal C}^{\mathrm {tf}}$
be such that
![]() $(v-\alpha )(x)=0$
. Then
$(v-\alpha )(x)=0$
. Then
![]() $\delta (x)\in {\cal D}^{\mathrm {tf}}$
is such that
$\delta (x)\in {\cal D}^{\mathrm {tf}}$
is such that
![]() $(v-\alpha )(\delta (x))=0$
; therefore, by the induction hypothesis there is
$(v-\alpha )(\delta (x))=0$
; therefore, by the induction hypothesis there is
![]() $m\ge 0$
and
$m\ge 0$
and
![]() $y\in {\cal D}^{v=\alpha }$
such that
$y\in {\cal D}^{v=\alpha }$
such that
![]() $y^{\mathrm {tf}}=p^m\delta (x)$
. Let
$y^{\mathrm {tf}}=p^m\delta (x)$
. Let
![]() $z\in {\cal C}$
be such that
$z\in {\cal C}$
be such that
![]() $\delta (z)=y$
and let
$\delta (z)=y$
and let
![]() $\tilde {x}\in {\cal C}$
be such that
$\tilde {x}\in {\cal C}$
be such that
![]() $\tilde {x}^{\mathrm {tf}}=x$
. Then there is
$\tilde {x}^{\mathrm {tf}}=x$
. Then there is
![]() $q\in \mathcal {B}$
such that
$q\in \mathcal {B}$
such that
![]() $\gamma (p^{m}q)-z+p^m\tilde {x}\in {\cal C}^{\mathrm {tors}}$
and so
$\gamma (p^{m}q)-z+p^m\tilde {x}\in {\cal C}^{\mathrm {tors}}$
and so
![]() $p^mz-p^{m+r}\gamma (q)=p^{m+r}\tilde {x}$
. Let
$p^mz-p^{m+r}\gamma (q)=p^{m+r}\tilde {x}$
. Let
![]() $t=p^mz-p^{m+r}\gamma (q)\in {\cal C}$
. It has the property that
$t=p^mz-p^{m+r}\gamma (q)\in {\cal C}$
. It has the property that
![]() $(v-\alpha )(t)=(v-\alpha )p^{m+r}(\tilde {x})$
and so
$(v-\alpha )(t)=(v-\alpha )p^{m+r}(\tilde {x})$
and so
![]() $(v-\alpha )(t)^{\mathrm {tf}}=0$
, that is,
$(v-\alpha )(t)^{\mathrm {tf}}=0$
, that is,
![]() $(v-\alpha )(t)\in {\cal C}^{\mathrm {tors}}$
. Therefore,
$(v-\alpha )(t)\in {\cal C}^{\mathrm {tors}}$
. Therefore,
![]() $(v-\alpha )(p^rt)=0$
and
$(v-\alpha )(p^rt)=0$
and
![]() $(p^rt)^{\mathrm {tf}}=p^{m+2r}x.$
$(p^rt)^{\mathrm {tf}}=p^{m+2r}x.$
Proof. (of Theorem 7.2) Let
![]() $\nu \in {\mathbb N}$
be large enough so that Lemma 7.3 is satisfied for the triple
$\nu \in {\mathbb N}$
be large enough so that Lemma 7.3 is satisfied for the triple
![]() $\Bigl (\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {Fil}}^{\nu }\bigr ), v=P(U_p), \alpha \Bigr )$
, and consider the exact sequence of sheaves on the pro-Kummer étale site
$\Bigl (\mathrm {H}^1\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, {\mathfrak {Fil}}^{\nu }\bigr ), v=P(U_p), \alpha \Bigr )$
, and consider the exact sequence of sheaves on the pro-Kummer étale site
![]() $\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}$
:
$\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}$
:
where we use the notations introduced before Lemma 7.4. It induces the long exact sequence of pro-Kummer étale cohomology groups which, in order to simplify notations, we write
![]() $\mathrm {H}^{\bullet }(F)$
instead of
$\mathrm {H}^{\bullet }(F)$
instead of
![]() $\mathrm {H}^{\bullet }\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, F\bigr )$
, where F is a sheaf on
$\mathrm {H}^{\bullet }\bigl ((\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}, F\bigr )$
, where F is a sheaf on
![]() $(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}$
.
$(\mathcal {X}_{\infty }^{(u)})_{\mathrm {pke}}$
.
 $$ \begin{align*}\begin{array}{ccccccccc} {\cal A}=\mathrm{H}^0({\mathfrak{D}}_k/{\mathfrak{Fil}}^{\nu})&\stackrel{\beta}{\rightarrow}&\mathcal{B}=\mathrm{ H}^1({\mathfrak{Fil}}^{\nu})&\stackrel{\gamma}{\rightarrow} &{\cal C}=\mathrm{H}^1({\mathfrak{D}}_k)\\&\stackrel{\delta}{\rightarrow} &{\cal D}=\mathrm{ H}^1({\mathfrak{D}}_k/{\mathfrak{Fil}}^{\nu})&\stackrel{\epsilon}{\rightarrow}&{\cal E}=\mathrm{H}^2({\mathfrak{Fil}}^{\nu}). \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccccccccc} {\cal A}=\mathrm{H}^0({\mathfrak{D}}_k/{\mathfrak{Fil}}^{\nu})&\stackrel{\beta}{\rightarrow}&\mathcal{B}=\mathrm{ H}^1({\mathfrak{Fil}}^{\nu})&\stackrel{\gamma}{\rightarrow} &{\cal C}=\mathrm{H}^1({\mathfrak{D}}_k)\\&\stackrel{\delta}{\rightarrow} &{\cal D}=\mathrm{ H}^1({\mathfrak{D}}_k/{\mathfrak{Fil}}^{\nu})&\stackrel{\epsilon}{\rightarrow}&{\cal E}=\mathrm{H}^2({\mathfrak{Fil}}^{\nu}). \end{array} \end{align*} $$
We’d like to show the v-module
![]() ${\cal C}$
satisfies the property
${\cal C}$
satisfies the property
![]() $(\ast )$
.
$(\ast )$
.
1) Let
![]() $x\in {\cal C}^{v=\alpha }$
such that x is a p-power torsion element. Then
$x\in {\cal C}^{v=\alpha }$
such that x is a p-power torsion element. Then
![]() $\delta (x)\in {\cal D}^{v=\alpha }$
is a p-power torsion element, and let
$\delta (x)\in {\cal D}^{v=\alpha }$
is a p-power torsion element, and let
![]() $s=s({\cal D})\in {\mathbb N}$
be such that
$s=s({\cal D})\in {\mathbb N}$
be such that
![]() $p^s\delta (x)=0$
. Then let
$p^s\delta (x)=0$
. Then let
![]() $y\in \mathcal {B}$
be such that
$y\in \mathcal {B}$
be such that
![]() $\gamma (y)=p^sx$
. We also have
$\gamma (y)=p^sx$
. We also have
![]() $\gamma \bigl ((v-\alpha )y\bigr )=(v-\alpha )\gamma (y)= (v-\alpha )(p^sx)=0$
. Therefore, let
$\gamma \bigl ((v-\alpha )y\bigr )=(v-\alpha )\gamma (y)= (v-\alpha )(p^sx)=0$
. Therefore, let
![]() $z\in {\cal A}$
be such that
$z\in {\cal A}$
be such that
![]() $\beta (z)=(v-\alpha )(y)$
.
$\beta (z)=(v-\alpha )(y)$
.
At this point, we recall the following result from [Reference Serre21], Proposition 12, and [Reference Coleman13], Propositions A.4.2 and A.4.3: As
![]() ${\cal A}[1/p]$
is a finitely generated, free
${\cal A}[1/p]$
is a finitely generated, free
![]() $R[1/p]$
-module and
$R[1/p]$
-module and
![]() $U_p$
is completely continuous on it, after localizing B to
$U_p$
is completely continuous on it, after localizing B to
![]() $B'$
and replacing R by
$B'$
and replacing R by
![]() $R'$
, there are
$R'$
, there are
![]() $d=d({\cal A},\alpha ), e=e({\cal A},\alpha )\in {\mathbb N}$
and
$d=d({\cal A},\alpha ), e=e({\cal A},\alpha )\in {\mathbb N}$
and
![]() $e_{\alpha }=p^dP_{\alpha }(U_p)$
, with
$e_{\alpha }=p^dP_{\alpha }(U_p)$
, with
![]() $p^dP_{\alpha }(T)$
a series with integral coefficients such that for every
$p^dP_{\alpha }(T)$
a series with integral coefficients such that for every
![]() $z\in {\cal A}$
we denote by
$z\in {\cal A}$
we denote by
![]() $z_{\alpha }:=e_{\alpha } z\in {\cal A}$
and by
$z_{\alpha }:=e_{\alpha } z\in {\cal A}$
and by
![]() $z^{\perp }:=p^dz-z_{\alpha }\in {\cal A}$
. Then
$z^{\perp }:=p^dz-z_{\alpha }\in {\cal A}$
. Then
![]() $(v-\alpha )(z_{\alpha })=0$
. Moreover there is a
$(v-\alpha )(z_{\alpha })=0$
. Moreover there is a
![]() $w_{\alpha }\in {\cal A}$
with
$w_{\alpha }\in {\cal A}$
with
![]() $(v-\alpha )(w_{\alpha })=p^ez_{\alpha }^{\perp }$
.
$(v-\alpha )(w_{\alpha })=p^ez_{\alpha }^{\perp }$
.
Let now
![]() $e,d$
be as above, then
$e,d$
be as above, then
![]() $p^{d+e}z=p^ez_{\alpha }+(v-\alpha )(w_{\alpha })$
. Therefore, we have:
$p^{d+e}z=p^ez_{\alpha }+(v-\alpha )(w_{\alpha })$
. Therefore, we have:
If we set
![]() $m:=p^{d+e}y-\beta (w_{\alpha })$
, we have
$m:=p^{d+e}y-\beta (w_{\alpha })$
, we have
![]() $(v-\alpha )^{2}(m)=0$
and
$(v-\alpha )^{2}(m)=0$
and
![]() $\gamma (m)=p^{d+e}\gamma (y)=p^{d+e+s}x$
. As
$\gamma (m)=p^{d+e}\gamma (y)=p^{d+e+s}x$
. As
![]() $(v-\alpha )^{2}m=0$
, we have
$(v-\alpha )^{2}m=0$
, we have
![]() $\alpha ^{2}m=0$
; therefore,
$\alpha ^{2}m=0$
; therefore,
![]() $\alpha ^{2}p^{d+e+s}x=0$
. This concludes 1) of property
$\alpha ^{2}p^{d+e+s}x=0$
. This concludes 1) of property
![]() $(\ast )$
for
$(\ast )$
for
![]() ${\cal C}$
.
${\cal C}$
.
2) Let
![]() $x\in \bigl ({\cal C}^{\mathrm {tf}}\bigr )^{v=\alpha }$
. Then there is
$x\in \bigl ({\cal C}^{\mathrm {tf}}\bigr )^{v=\alpha }$
. Then there is
![]() $r:=r({\cal D},\alpha )$
and
$r:=r({\cal D},\alpha )$
and
![]() $y\in {\cal D}^{v=\alpha }$
such that
$y\in {\cal D}^{v=\alpha }$
such that
![]() $y^{\mathrm { tf}}=p^r\delta (x)$
, where we denoted
$y^{\mathrm { tf}}=p^r\delta (x)$
, where we denoted
![]() $y^{\mathrm {tf}}$
the image of y in
$y^{\mathrm {tf}}$
the image of y in
![]() ${\cal D}^{\mathrm {tf}}$
. The image
${\cal D}^{\mathrm {tf}}$
. The image
![]() $\epsilon (y)\in {\cal E}^{v=\alpha }$
is annihilated by
$\epsilon (y)\in {\cal E}^{v=\alpha }$
is annihilated by
![]() $\alpha $
, and therefore, there is
$\alpha $
, and therefore, there is
![]() $z\in {\cal C}$
such that
$z\in {\cal C}$
such that
![]() $\delta (z)=\alpha y$
. There is
$\delta (z)=\alpha y$
. There is
![]() $w\in {\cal D}$
such that
$w\in {\cal D}$
such that
![]() $(v-\alpha )(z)=\gamma (w)$
and let
$(v-\alpha )(z)=\gamma (w)$
and let
![]() $q\in \mathcal {B}$
be such that
$q\in \mathcal {B}$
be such that
![]() $\alpha w=(v-\alpha )(q)$
. Therefore,
$\alpha w=(v-\alpha )(q)$
. Therefore,
![]() $(v-\alpha )(\alpha z-\gamma (q))=0$
. Let
$(v-\alpha )(\alpha z-\gamma (q))=0$
. Let
![]() $\tilde {x}:=\alpha z-\gamma (q)\in {\cal C}^{v=\alpha }$
. Then
$\tilde {x}:=\alpha z-\gamma (q)\in {\cal C}^{v=\alpha }$
. Then
![]() $\delta (\tilde {x})=\delta (\alpha z)=\alpha ^2 y$
. The image
$\delta (\tilde {x})=\delta (\alpha z)=\alpha ^2 y$
. The image
![]() $\alpha ^2 y^{\mathrm {tf}}$
of
$\alpha ^2 y^{\mathrm {tf}}$
of
![]() $\alpha ^2 y$
in
$\alpha ^2 y$
in
![]() $({\cal D}[1/p])^{v=\alpha }$
is
$({\cal D}[1/p])^{v=\alpha }$
is
![]() $\alpha ^2 p^r \delta (x)$
. But
$\alpha ^2 p^r \delta (x)$
. But
![]() $\delta $
induces an isomorphism
$\delta $
induces an isomorphism
![]() $\displaystyle \bigl ({\cal C}[1/p] \bigr )^{v=\alpha }\stackrel {\delta }{\cong } \bigl ({\cal D}[1/p] \bigr )^{v=\alpha }$
(see [Reference Andreatta, Iovita and Stevens6]). Therefore, the image
$\displaystyle \bigl ({\cal C}[1/p] \bigr )^{v=\alpha }\stackrel {\delta }{\cong } \bigl ({\cal D}[1/p] \bigr )^{v=\alpha }$
(see [Reference Andreatta, Iovita and Stevens6]). Therefore, the image
![]() $(\tilde {x})^{\mathrm {tf}}$
of
$(\tilde {x})^{\mathrm {tf}}$
of
![]() $\tilde {x}$
in
$\tilde {x}$
in
![]() $\bigl ({\cal C}[1/p] \bigr )^{v=\alpha }$
is
$\bigl ({\cal C}[1/p] \bigr )^{v=\alpha }$
is
![]() $\alpha ^2p^r x$
which proves the claim.
$\alpha ^2p^r x$
which proves the claim.







