Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T19:49:04.824Z Has data issue: false hasContentIssue false
  • English
  • Français

TATE’S CONJECTURE AND THE TATE–SHAFAREVICH GROUP OVER GLOBAL FUNCTION FIELDS

Part of: Surfaces and higher-dimensional varieties Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  17 September 2019

Thomas H. Geisser Open the ORCID record for Thomas H. Geisser [Opens in a new window]
Thomas H. Geisser*
Affiliation:
Rikkyo University, Ikebukuro, Tokyo, Japan (geisser@rikkyo.ac.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 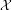${\mathcal{X}}$ be a regular variety, flat and proper over a complete regular curve over a finite field such that the generic fiber 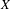$X$ is smooth and geometrically connected. We prove that the Brauer group of 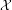${\mathcal{X}}$ is finite if and only Tate’s conjecture for divisors on 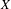$X$ holds and the Tate–Shafarevich group of the Albanese variety of 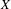$X$ is finite, generalizing a theorem of Artin and Grothendieck for surfaces to arbitrary relative dimension. We also give a formula relating the orders of the group under the assumption that they are finite, generalizing the known formula for a surface.

Keywords

Brauer groupTate–Shafarevich groupTate’s conjecture

MSC classification

Primary: 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Secondary: 14G17: Positive characteristic ground fields 14J20: Arithmetic ground fields 11G25: Varieties over finite and local fields 11G35: Varieties over global fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 3 , May 2021 , pp. 1001 - 1022
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported by JSPS Grant-in-Aid (A) 15H02048-1, (C) 18K03258

References

Beilinson, A. A., Height pairings between algebraic cycles, in K-theory, Arithmetic and Geometry (Moscow, 1984–1986), Lecture Notes in Mathematics, Volume 1289, pp. 1–25 (Springer, Berlin, 1987).Google Scholar
Colliot-Thélène, J. L., Cycles algébriques de torsion et K-théorie algébrique, in Arithmetic Algebraic Geometry (Trento, 1991), Lecture Notes in Mathematics, Volume 1553, pp. 1–49 (Springer, Berlin, 1993).CrossRefGoogle Scholar
Colliot-Thélène, J. L., Groupe de Chow des zéro-cycles sur les variétés p-adiques (d’après S. Saito, K. Sato et al.). Séminaire Bourbaki. Vol. 2009/2010. Exposés 1012–1026. Astérisque No. 339 (2011), Exp. No. 1012, vii, 1–30.Google Scholar
de Jong, J. A., Smoothness, semi-stability and alterations, Inst. Hautes Études Sci. Publ. Math. 83 (1996), 51–93.CrossRefGoogle Scholar
Deligne, P., La formule de dualite globale, in Théorie des topos et cohomologie étale des schémas. Tome 3. Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (ed. Artin, Dirigé par M., Grothendieck, A. and Verdier, J. L.), Lecture Notes in Mathematics, Volume 305, p. vi+640 (Springer, Berlin–New York, 1973).Google Scholar
Gabber, O., Sur la torsion dans la cohomologie l-adique d’une variétè, C. R. Acad. Sci. Paris Sér. I Math. 297(3) (1983), 179–182.Google Scholar
Geisser, T., Motivic cohomology over Dedekind rings, Math. Z. 248(4) (2004), 773–794.CrossRefGoogle Scholar
Geisser, T., Duality via cycle complexes, Ann. of Math. (2) 172(2) (2010), 1095–1126.CrossRefGoogle Scholar
Geisser, T., On the structure of etale motivic cohomology, J. Pure Appl. Algebra 221(7) (2017), 1614–1628.10.1016/j.jpaa.2016.12.019CrossRefGoogle Scholar
Geisser, T., Duality of integral étale motivic cohomology, in K-Theory-Proceedings of the International Colloquium, Mumbai, 2016, pp. 195–209 (Hindustan Book Agency, New Delhi, 2018).Google Scholar
Geisser, T., Comparing the Brauer group and the Tate–Shafarevich group, J. Inst. Math. Jussieu. to appear, doi:10.1017/S1474748018000294.Google Scholar
Geisser, T. and Levine, M., The Bloch–Kato conjecture and a theorem of Suslin-Voevodsky, J. Reine Angew. Math. 530 (2001), 55–103.Google Scholar
González-Avilés, C. D. and Tan, K.-S., A generalization of the Cassels-Tate dual exact sequence, Math. Res. Lett. 14(2) (2007), 295–302.CrossRefGoogle Scholar
Grothendieck, A., Le groupe de Brauer. III, in Exemples et compléments. Dix exposés sur la cohomologie des schémas, 88–188, Advanced Studies in Pure Mathematics, Volume 3 (North-Holland, Amsterdam, 1968).Google Scholar
Illusie, L., Laszlo, Y. and Orgogozo, F., Travaux de Gabber sur l’uniformisation locale et la cohomologie étale des schémas quasi-excellents, in Séminaire à l’École Polytechnique 2006–2008, Astérisque No. 363–364 (Société Mathématique de France, Paris, 2014).Google Scholar
Jannsen, U., On the l-adic cohomology of varieties over number fields and its Galois cohomology, in Galois Groups Over ℚ (Berkeley, CA, 1987), Mathematical Sciences Research Institute Publications, Volume 16, pp. 315–360 (Springer, New York, 1989).CrossRefGoogle Scholar
Jannsen, U., Saito, S. and Sato, K., Étale duality for constructible sheaves on arithmetic schemes, J. Reine Angew. Math. 688 (2014), 1–65.CrossRefGoogle Scholar
Kahn, B., Algebraic K-theory, algebraic cycles and arithmetic geometry, in Handbook of K-theory, Volume 1, 2, pp. 351–428 (Springer, Berlin, 2005).CrossRefGoogle Scholar
Kato, K. and Trihan, F., On the conjectures of Birch and Swinnerton–Dyer in characteristic p > 0, Invent. Math. 153(3) (2003), 537–592.CrossRefGoogle Scholar
Kerz, M. and Saito, S., Cohomological Hasse principle and motivic cohomology for arithmetic schemes, Publ. Math. Inst. Hautes Études Sci. 115 (2012), 123–183.CrossRefGoogle Scholar
Lang, S., Abelian varieties, in Interscience Tracts in Pure and Applied Mathematics p. xii+256 (No. 7 Interscience Publishers, Inc., New York, 1959). Interscience Publishers Ltd., London.Google Scholar
Levine, M., K-theory and motivic cohomology of schemes, https://faculty.math.illinois.edu/K-theory/0336/mot.pdf.Google Scholar
Lichtenbaum, S., Duality theorems for curves over p-adic fields, Invent. Math. 7 (1969), 120–136.CrossRefGoogle Scholar
Liu, Q., Lorenzini, D. and Raynaud, M., On the Brauer group of a surface, Invent. Math. 159(3) (2005), 673–676.CrossRefGoogle Scholar
Milne, J. S., Jacobian varieties, in Arithmetic Geometry (Storrs, Conn., 1984), pp. 167–212 (Springer, New York, 1986).CrossRefGoogle Scholar
Milne, J., Values of zeta functions of varieties over finite fields, Amer. J. Math. 108(2) (1986), 297–360.CrossRefGoogle Scholar
Milne, J. S., Arithmetic Duality Theorems, Second Edition p. viii+339 (BookSurge, LLC, Charleston, SC, 2006). ISBN: 1-4196-4274-X.Google Scholar
Morrow, M., A Variational Tate Conjecture in crystalline cohomology, J. Eur. Math. Soc., to appear, https://arxiv.org/pdf/1408.6783.pdf.Google Scholar
Saito, S. and Sato, K., A finiteness theorem for zero-cycles over p-adic fields. With an appendix by Uwe Jannsen, Ann. of Math. (2) 172(3) (2010), 1593–1639.CrossRefGoogle Scholar
Saito, S. and Sato, K., Zero-cycles on varieties over p-adic fields and Brauer groups, Ann. Sci. Éc. Norm. Supér. (4) 47(3) (2014), 505–537.CrossRefGoogle Scholar
Sato, K., p-adic étale Tate twists and arithmetic duality, Ann. Sci. Éc. Norm. Supér. (4) 40(4) (2007), 519–588. With an appendix by Kei Hagihara.CrossRefGoogle Scholar
Spaltenstein, N., Resolutions of unbounded complexes, Compos. Math. 65(2) (1988), 121–154.Google Scholar
Thomason, R. W., Algebraic K-theory and étale cohomology, Ann. Sci. Éc. Norm. Supér. (4) 18(3) (1985), 437–552.CrossRefGoogle Scholar
Zhong, C., Comparison of dualizing complexes, J. Reine Angew. Math. 695 (2014), 1–39.CrossRefGoogle Scholar