Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T13:59:09.174Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic cycles on the relative symmetric powers and on the relative Jacobian of a family of curves. II

Part of: Cycles and subschemes

Published online by Cambridge University Press:  23 March 2010

Ben Moonen  and
Alexander Polishchuk
Ben Moonen
Affiliation:
Department of Mathematics, University of Amsterdam, PO Box 94248, 1090 GE Amsterdam, The Netherlands, (b.j.j.moonen@uva.nl)
Alexander Polishchuk
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR 97403, USA, (apolish@uoregon.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let C be a family of curves over a non-singular variety S. We study algebraic cycles on the relative symmetric powers C[n] and on the relative Jacobian J. We consider the Chow homology CH*(C[∙]/S) := ⊕n CH*(C[n]/S) as a ring using the Pontryagin product. We prove that CH*(C[∙]/S) is isomorphic to CH*(J/S)[t]〈u〉, the PD-polynomial algebra (variable: u) over the usual polynomial ring (variable: t) over CH*(J/S). We give two such isomorphisms that over a general base are different. Further we give precise results on how CH*(J/S) sits embedded in CH*(C[∙]/S) and we give an explicit geometric description of how the operators 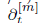and ∂u act. This builds upon the study of certain geometrically defined operators Pi,j (a) that was undertaken by one of us.

Our results give rise to a new grading on CH*(J/S). The associated descending filtration is stable under all operators [N]*, and [N]* acts on 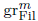as multiplication by Nm. Hence, after − ⊗ ℚ this filtration coincides with the one coming from Beauville's decomposition. The grading we obtain is in general different from Beauville's.

Finally, we give a version of our main result for tautological classes, and we show how our methods give a simple geometric proof of some relations obtained by Herbaut and van der Geer–Kouvidakis, as later refined by one of us.

Keywords

symmetric products of curvesJacobiansChow ringsalgebraic cyclesmotives

MSC classification

Secondary: 14C15: (Equivariant) Chow groups and rings; motives 14C25: Algebraic cycles
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 9 , Issue 4 , October 2010 , pp. 799 - 846
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Beauville, A. and Voisin, C., On the Chow ring of a K3 surface, J. Alg. Geom. 13 (2004), 417–426.Google Scholar
2.Colombo, E. and van Geemen, B., Note on curves in a Jacobian, Compositio Math. 88 (1993), 333–353.Google Scholar
3.Deninger, C. and Murre, J., Motivic decomposition of abelian schemes and the Fourier transform, J. Reine Angew. Math. 422 (1991), 201–219.Google Scholar
4.Fulton, W., Intersection theory, 2nd edn, Ergebnisse der Mathematik und ihrer Grenzgebiete, 3 Folge, Volume 2 (Springer, 1998).Google Scholar
5.Gross, B. and Schoen, C., The modified diagonal cycle on the triple product of a pointed curve, Annales Inst. Fourier 45(3) (1995), 649–679.CrossRefGoogle Scholar
6.Herbaut, F., Algebraic cycles on the Jacobian of a curve with a linear system of given dimension, Compositio Math. 143 (2007), 883–899.CrossRefGoogle Scholar
7.Jannsen, U., Motivic sheaves and filtrations on Chow groups, in Motives (Seattle, WA, 1991), Proceedings of Symposia in Pure Mathematics, Volume 55, Part 1, pp. 245–302 (American Mathematical Society, Providence, RI, 1994).Google Scholar
8.Kimura, S.-I. and Vistoli, A., Chow rings of infinite symmetric products, Duke Math. J. 85(2) (1996), 411–430.CrossRefGoogle Scholar
9.Künnemann, K., On the Chow motive of an abelian scheme, in Motives (Seattle, WA, 1991), Proceedings of Symposia in Pure Mathematics, Volume 55, Part 1, pp. 189–205 (American Mathematical Society, Providence, RI, 1994).Google Scholar
10.Looijenga, E., On the tautological ring of M g, Invent. Math. 121(2) (1995), 411–419.CrossRefGoogle Scholar
11.Milne, J. S., Zero cycles on algebraic varieties in nonzero characteristic: Rojtman's theorem, Compositio Math. 47(3) (1982), 271–287.Google Scholar
12.Moonen, B., Relations between tautological cycles on Jacobians, Comment. Math. Helv. 84(3) (2009), 471–502.Google Scholar
13.Moonen, B. and Polishchuk, A., Divided powers in Chow rings and integral Fourier transforms, Adv. Math., in press (doi:10.1016/j.aim.2009.12.025).CrossRefGoogle Scholar
14.Murre, J., On a conjectural filtration on the Chow groups of an algebraic variety, I, The general conjectures and some examples, Indagationes Math. 4 (1993), 177–188.CrossRefGoogle Scholar
15.Polishchuk, A., Lie symmetries of the Chow group of a Jacobian and the tautological subring, J. Alg. Geom. 16(3) (2007), 459–476.Google Scholar
16.Polishchuk, A., Algebraic cycles on the relative symmetric powers and on the relative Jacobian of a family of curves, I, Selecta Math. 13 (2007), 531–569.Google Scholar
17.Rojtman, A. A., The torsion of the group of 0-cycles modulo rational equivalence, Annals Math. (2) 111(3) (1980), 553–569.CrossRefGoogle Scholar
18.Scholl, A. J., Classical motives, in Motives (Seattle, WA, 1991), Proceedings of Symposia in Pure Mathematics, Volume 55, Part 1, pp. 163–187 (American Mathematical Society, Providence, RI, 1994).Google Scholar
19.Shermenev, A. M., Motif of an Abelian variety, Funct. Analysis Applic. 8 (1974), 47–53.CrossRefGoogle Scholar
20.van der Geer, G. and Kouvidakis, A., Cycle relations on Jacobian varieties (with an appendix by Don Zagier), Compositio Math. 143 (2007), 900–908.CrossRefGoogle Scholar