Electrical Properties of Oxygen Doped GaN Grown by Metalorganic Vapor Phase Epitaxy

Abstract

Deliberate oxygen doping of GaN grown by MOVPE has been studied. The electron concentration increased as the square root of the oxygen partial pressure. Oxygen is a shallow donor with a thermal ionization energy of 27 ±2 meV. A compensation ratio of Θ = 0.3-0.4 was determined from Hall effect measurements. The formation energy of O_N of E^F = 1.3 eV, determined from the experimental data, is lower than the theoretically predicted value.

Introduction

The origin of n-type conductivity in epitaxial GaN is of continuing interest. Residual electron concentration of undoped epitaxial GaN typically ranges from 10¹⁶ to 10¹⁹ cm⁻³. Although the n-type conductivity was initially attributed to nitrogen vacancies, residual impurities such as oxygen and silicon are believed to be at least partially responsible for the high conductivity [1]. Oxygen substitutes for nitrogen behaving as a donor in GaN [1]. Several secondary ion mass spectroscopy (SIMS) studies of unintentionally doped GaN have observed large concentrations of O and Si [2-3,6]. The source of oxygen is believed to be in the ammonia used for metalorganic vapor phase epitaxial (MOVPE) growth. These observations are consistent with recent total energy calculations of van de Walle et al [1] that indicated that the solubility of O_N is relatively high in wurtzite GaN. Despite its importance, the nature of oxygen donors in GaN remains controversial [3,8]. Initial work on the deliberately oxygen doped GaN indicated that oxygen is a “shallow” deep donor with apparent activation energy of 78 meV as determined by optical measurements from the position of the donor bound exciton [4]. Since then, several groups have studied the electrical properties of both deliberate [3,5] and unintentionally oxygen doped materials [2,6-8,18]. Temperature dependent Hall effect measurements indicated that oxygen donors are shallow with a thermal ionization energy ranging from: 4-29 meV [2-3,6,7]. In contrast to these measurements, Chen et al subsequently indicated that substitutional oxygen is a deep donor with an activation energy close to 0.9 eV [8]. This was based on the observation of an infra-red photoluminescence (PL) emission band on an unintentionally doped GaN. In this paper we present results of the study of deliberate oxygen doping of high purity epitaxial GaN. Upon doping the electron concentration increased from 1×10¹⁷ to 3×10¹⁹ cm⁻³. Oxygen is shown to behave as a simple donor in GaN. From defect equilibria studies, the formation energy of substitutional oxygen is calculated and compared to recent total energy calculations.

Experimental

Epitaxial GaN layers were grown by MOVPE onto the c-plane of sapphire substrates in an atmospheric pressure horizontal flow reactor using the reactants: trimethylgallium and ammonia. A Nanochem purifier was utilized to eliminate residual moisture and oxygen from the ammonia gas. Undoped as-grown GaN layers had free electron concentrations and mobilities of 0.9-1×10¹⁷ cm⁻³ and 420-500 cm²V⁻¹s⁻¹, respectively. Two oxygen-nitrogen gas mixtures were used as a dopant source (20 and 520 ppm of oxygen in nitrogen, respectively). The epitaxial layer consisted of a 20 nm GaN nucleation layer, a thin 50 nm undoped layer, and a two micron thick oxygen doped layer. Doped layers were grown at 1060°C. Hall measurements were performed using the van der Pauw geometry over the temperature range of 77-330 K. The ohmicity of the indium contacts were verified over all temperatures.

Dependence of Carrier Concentration on Oxygen Partial Pressure

For substitution of oxygen on a nitrogen site the defect equilibrium equation is given by:

(1)

where K₀ is the equilibrium constant and is given by exp[- G^F/kT] . The free energy G^F = E^F- TS^F for oxygen substitution can be obtained using first principles, total energy calculations. The value of E^F is given by [17]:

(2)

where E_tot is the energy of the neutral defect, μ_O and μ_N are the chemical potentials of oxygen and nitrogen , q is a charge state of defect and E_F is the Fermi energy. The chemical potential of oxygen is given by μ_O = kTlnf_O= kTln(K₀P(O₂)^1/2). The O_N concentration is thus given by:

(3)

where N_site is the substitional oxygen site density and T is the growth temperature. The entropy contribution is assumed to be small. The carrier concentration and its dependence on oxygen partial pressure can be obtained from the charge neutrality condition:

(4)

-where Θ is the compensation ratio N_A/N_D. Since the oxygen donor is shallow, n ≈ N_D - N_A. The carrier concentration can be calculated once the compensation ratio Θ is known. It has been shown for n-type GaN the compensation ratio is nearly independent of donor concentration and is of the order of 0.4 [10]. The theoretical expression of the free electron concentration versus oxygen partial pressure can be calculated at growth temperature [9-10] using Eqns. 1-4, where the site density N_site= 4.4×10²² cm⁻³ and the effective density of states is given by N_c = 4.98×10¹⁴T^3/2.

Fig. 1 shows the dependence of carrier concentration on oxygen dopant partial pressure. The carrier concentration increases as the square root of oxygen partial pressure up to 7×10¹⁸ cm⁻³. The solid line is the calculated dependence of the free electron concentration on oxygen partial pressure using the formation energy as a fitting parameter. There is good agreement between theory and experimental data up to 7×10¹⁸ cm⁻³, as seen in Fig. 1 for a formation energy of 1.3 eV. Since the measured electron concentration is directly proportional to the square root of the oxygen partial pressure and proportional to the oxygen donor concentration, it can be concluded that oxygen is a simple donor in GaN. The measured oxygen solubility, however, differs from theoretical prediction. According to calculations of Van de Walle et al the oxygen concentration should not exceed 10¹⁸ cm⁻³ for Ga rich growth conditions and 3×10¹⁶ cm⁻³ for N-rich conditions where E^F = 1.8 and 2.2 eV, respectively [1,17]. The calculated formation energy is the lowest under Ga-rich conditions. For these conditions the solubility of oxygen is limited by the formation of Ga₂O₃: 2μ_Ga + 3μ_O < μ(Ga₂O₃). Since oxygen doped GaN epitaxial layers, however, are grown under N rich conditions, [21] the experimentally determined formation energy and the calculated value are not in good agreement. They differ by 0.9 eV. The theory underestimates the solubility of oxygen by two orders of magnitude.

The results of our oxygen doping experiments are, nevertheless, consistent with existing data on oxygen doping of GaN. Niebuhr et al [5] using N₂O as an oxygen dopant source showed that the electron concentration increased with N₂O partial pressure and saturated at a level of 4×10¹⁸ cm⁻³. SIMS studies on oxygen contaminated epitaxial GaN by Forte-Poisson et al [2] indicated that the electron concentration is directly proportional to the amount of incorporated oxygen up to a concentration level of 6×10¹⁹ cm⁻³, which is consistent with oxygen behaving as a simple shallow donor.

Compensation of Oxygen Doped thin Films

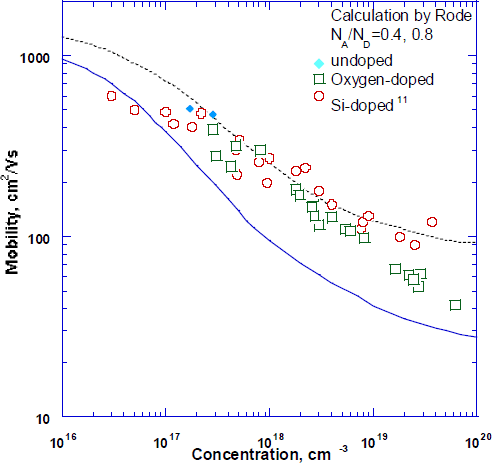
To determine the compensation ratio the electron mobility of oxygen doped GaN was measured and plotted as a function of carrier concentration as shown in Fig. 2. For comparison, the Hall mobilities of undoped and oxygen and Si [11] doped samples are also presented. The theoretical calculation of mobility by Rode [10] is also shown for compensation ratios of Θ = 0.4, 0.8. It can be seen from the plot that the O-doped samples have Θ = 0.4 for concentration up to 8×10¹⁸ cm⁻³. The compensation ratio increases however, from 0.4 to 0.6 for dopant concentrations in excess of 8×10¹⁸ cm⁻³. The compensation ratio of 0.4 for oxygen doped samples is comparable to that of Si-doped and Se-doped material suggesting the same defect is compensating the films [11,16].

Fig. 1 Electron concentration versus partial pressure for oxygen-doped GaN

Fig. 2 Mobility versus carrier concentration for undoped, O and Si-doped films. Calculated mobilities of Rode are given

Determination of Ionization Energy of O_N

The temperature dependence of the Hall effect was measured to obtain the thermal ionization energy of the donors in both undoped and doped films. Analysis of the donor activation energy in GaN is complicated by the presence of a large contribution by impurity band conduction [6,18-19]. Typically, impurity band conduction in semiconductors is observed at low temperature (T < 10 K) when donor freezeout occurs. However the large unintentional doping and compensation in GaN, decrease electron mobility resulting in conduction via impurity bands even at 77 K. To determine the donor activation energy several techniques have been utilized to account for impurity band conduction at low temperature [2,12-13]. However, all these methods which are used to eliminate the effects of the low temperature tail of the impurity band can potentially lead to a large variation in the calculated activation energy. For the present study a single donor model was used for oxygen doped films, whereas a two donor, one compensating acceptor model was used for the undoped films.

The activation energy of the oxygen donors was determined from temperature dependent Hall effect measurements. The data is shown in Fig. 3. The carrier concentration for undoped samples was corrected for the Hall factor r = <τ(E)²>/<τ>² found from the mobility data [9] . The activation energy and free electron concentration for the donor is calculated using the following equation [13]:

(6)

- where φ = g₀/g₁N_cT ^3/2exp(-E_D/kT), with the degeneracy of the unoccupied donor state g₀ = 1, the degeneracy of the occupied state g₁ = 2 and E_D is the activation energy of the donor. The acceptor concentration for undoped samples was found from mobility data. The measured electron concentration and activation energies are reported in Table 1. For undoped samples using a two-donor model, the activation energy of shallow and deep donors are 10 ± 2 and 52 ± 2 meV, respectively. Similar activation energies were obtained previously for the undoped samples [7,12]. A donor activation energy of less than 20 meV in GaN is attributed to a hydrogenic donor in the presence of screening [12]. The donor ionization energy in oxygen doped samples had an activation energy of 27 ± 2 meV. With increase in oxygen donor concentration impurity conductivity plays an ever more important role at low temperature, as seen in Fig. 3. At electron concentration ∼ 10¹⁹cm⁻³ the slope of the carrier concentration versus reciprocal temperature decreases, suggesting that at this concentration GaN becomes degenerate.

To determine the concentration of compensating acceptors, the temperature dependent mobility was analyzed for undoped samples based on the approach taken by D. C. Look [10]. The mobility is calculated by solving the Boltzmann equation using the relaxation-time approximation. The mobility is given by μ_H = e<τ(E)²>/m*<τ(E)>, where the brackets denote the average of relaxation time over electron energy E. The relaxation time τ(E) is given as:

(7)

where the relaxation times τ_acτ_poτ_peτ_ii are due to an acoustic, polar-optical modes and piezoelectric, ionized scattering, respectively. The constants utilized in calculations are given in Ref. [12,20].

Fig. 3 Free electron concentration with respect to temperature data for doped and undoped * GaN. The caculated dependece is shown with solid lines

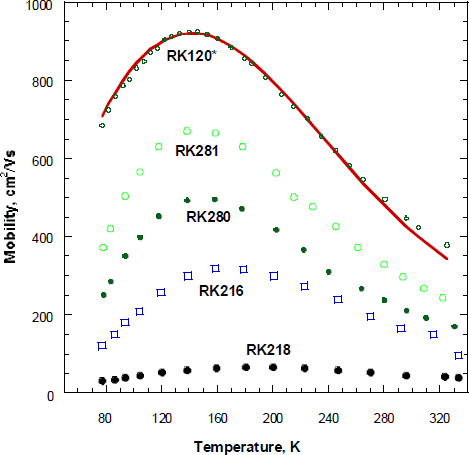
Fig.4 Mobility versus temperature for undoped * and doped GaN film. Theoretical curve is given by solid line

Table 1. Electronic characteristics of oxygen doped * and undoped samples calculated using Eqn.6-7.

From the fit, shown in Fig. 4 the acceptor concentration, and compensation ratio,θ ∼ 0.3 were determined and are reported in Table 1. At low temperature the calculated mobility of oxygen doped samples differed significantly from the measured mobility due to large impurity band conduction.

Conclusions

The doping of GaN by oxygen prepared by MOVPE was studied. The free electron concentration increases as the square root of oxygen partial pressure up to a concentration of 7×10¹⁸ cm⁻³. From the dependence of carrier concentration on oxygen partial pressure, it is concluded that oxygen behaves as a simple donor. The donor ionization energy is 27 ± 2 meV. Temperature dependent mobility and Hall measurements of O-doped samples indicate a constant compensation ratio of Θ = 0.3-0.4. Based on the experimental data the calculated formation energy of O_N in GaN is 1.3 eV.