No CrossRef data available.
Article contents
New pancake series for π
Published online by Cambridge University Press: 18 June 2020
Extract
In [1], Dalzell proved that 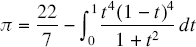 $\pi = \frac{{22}}{7} - \int_0^1 {\frac{{{t^4}{{(1 - t)}^4}}}{{1 + {t^2}}}}$
. He then used this equation to derive a new series converging to π. In [2], Backhouse studied the general case of integrals of the form
$\pi = \frac{{22}}{7} - \int_0^1 {\frac{{{t^4}{{(1 - t)}^4}}}{{1 + {t^2}}}}$
. He then used this equation to derive a new series converging to π. In [2], Backhouse studied the general case of integrals of the form 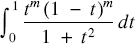 $\int_0^1 {\frac{{{t^m}{{(1 - t)}^m}}}{{1 + {t^2}}}dt}$
and derived conditions on m and n so that they could be used to evaluate π. As a sequel, he derived accurate rational approximations of π. This work was extended in [3] where new rational approximations of π are obtained. Some related integrals of the forms
$\int_0^1 {\frac{{{t^m}{{(1 - t)}^m}}}{{1 + {t^2}}}dt}$
and derived conditions on m and n so that they could be used to evaluate π. As a sequel, he derived accurate rational approximations of π. This work was extended in [3] where new rational approximations of π are obtained. Some related integrals of the forms 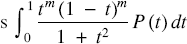 $\int_0^1 {\frac{{{t^m}{{(1 - t)}^m}}}{{1 + {t^2}}}P(t)\,dt}$
and
$\int_0^1 {\frac{{{t^m}{{(1 - t)}^m}}}{{1 + {t^2}}}P(t)\,dt}$
and 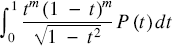 $\int_0^1 {\frac{{{t^m}{{(1 - t)}^m}}}{{\sqrt {1 - {t^2}} }}P(t)dt}$
with P(t) being of polynomial form are also investigated. In [4] the author gives more new approximations and new series for the case m = n = 4k. In [5] new series for π are obtained with the integral
$\int_0^1 {\frac{{{t^m}{{(1 - t)}^m}}}{{\sqrt {1 - {t^2}} }}P(t)dt}$
with P(t) being of polynomial form are also investigated. In [4] the author gives more new approximations and new series for the case m = n = 4k. In [5] new series for π are obtained with the integral 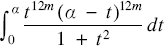 $\int_0^a {\frac{{{t^{12m}}{{(a - t)}^{12m}}}}{{1 + {t^2}}}dt}$
where
$\int_0^a {\frac{{{t^{12m}}{{(a - t)}^{12m}}}}{{1 + {t^2}}}dt}$
where 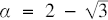 $a = 2 - \sqrt 3$
. The general problem of improving the convergence speed of the arctan series by transformation of the argument has also been considered in [6, 7]. In the present work the author considers an alternative form for the denominators in integrals. As a result, new series are obtained for multiples of π by some algebraic numbers.
$a = 2 - \sqrt 3$
. The general problem of improving the convergence speed of the arctan series by transformation of the argument has also been considered in [6, 7]. In the present work the author considers an alternative form for the denominators in integrals. As a result, new series are obtained for multiples of π by some algebraic numbers.
- Type
- Articles
- Information
- Copyright
- © Mathematical Association 2020



