Addenda to processes defined on a finite Markov chain
Published online by Cambridge University Press: 24 October 2008
Extract
Introduction. Two previous papers (1,2) have dealt with additive processes defined on finite Markov chains. Such a process in discrete time may be treated as a bivariate Markov process {R(k), X(k)}. The process R(k) is an irreducible Markov chain on states r = 1, 2, …, R governed by a stochastic transition matrix B0 with components brs. The marginal process X(k) ‘defined’ on the chain R(k) is a sum 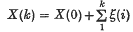 of random increments ξ(i) dependent on the chain, i.e. if the ith transition takes the chain from state r to state s, ξ,(i) is chosen from a distribution function Drs(x) indexed by r and s. The distribution of the bivariate process may be represented by a vector F(x, k) with components
of random increments ξ(i) dependent on the chain, i.e. if the ith transition takes the chain from state r to state s, ξ,(i) is chosen from a distribution function Drs(x) indexed by r and s. The distribution of the bivariate process may be represented by a vector F(x, k) with components
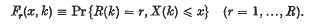
These are generated recursively by the relation
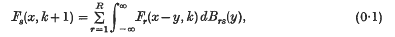
where the increment matrix distribution B(x) has components brsDrs(x). We denote the nth moment of B(x) by Bn = ∫xndB(x), so that B0 = B(∞).
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 63 , Issue 1 , January 1967 , pp. 187 - 193
- Copyright
- Copyright © Cambridge Philosophical Society 1967
References
REFERENCES
- 15
- Cited by

