Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hoppen, Carlos
Lefmann, Hanno
and
Odermann, Knut
2017.
A Rainbow Erdös--Rothschild Problem.
SIAM Journal on Discrete Mathematics,
Vol. 31,
Issue. 4,
p.
2647.
Hoppen, Carlos
Lefmann, Hanno
and
Odermann, Knut
2017.
On graphs with a large number of edge-colorings avoiding a rainbow triangle.
European Journal of Combinatorics,
Vol. 66,
Issue. ,
p.
168.
Hoppen, Carlos
Lefmann, Hanno
Odermann, Knut
and
Sanches, Juliana
2018.
Edge‐colorings avoiding rainbow stars.
Journal of Graph Theory,
Vol. 87,
Issue. 4,
p.
399.
Clemens, Dennis
Das, Shagnik
and
Tran, Tuan
2018.
Colourings without monochromatic disjoint pairs.
European Journal of Combinatorics,
Vol. 70,
Issue. ,
p.
99.
Hoppen, Carlos
and
Lefmann, Hanno
2019.
Remarks on an Edge-coloring Problem.
Electronic Notes in Theoretical Computer Science,
Vol. 346,
Issue. ,
p.
511.
Das, Shagnik
Glebov, Roman
Sudakov, Benny
and
Tran, Tuan
2019.
Colouring set families without monochromatic k-chains.
Journal of Combinatorial Theory, Series A,
Vol. 168,
Issue. ,
p.
84.
Falgas‐Ravry, Victor
O'Connell, Kelly
and
Uzzell, Andrew
2019.
Multicolor containers, extremal entropy, and counting.
Random Structures & Algorithms,
Vol. 54,
Issue. 4,
p.
676.
Hoppen, Carlos
Lefmann, Hanno
and
Nolibos, Denilson
2021.
An extension of the rainbow Erdős-Rothschild problem.
Discrete Mathematics,
Vol. 344,
Issue. 8,
p.
112443.
Hoppen, Carlos
Lefmann, Hanno
and
Nolibos, Denilson Amaral
2021.
Extended Abstracts EuroComb 2021.
Vol. 14,
Issue. ,
p.
533.
de Oliveira Contiero, Lucas
Hoppen, Carlos
Lefmann, Hanno
and
Odermann, Knut
2021.
Rainbow Erdös--Rothschild Problem for the Fano Plane.
SIAM Journal on Discrete Mathematics,
Vol. 35,
Issue. 3,
p.
1927.
Botler, Fábio
Hoppen, Carlos
and
Mota, Guilherme Oliveira
2022.
Counting orientations of graphs with no strongly connected tournaments.
Discrete Mathematics,
Vol. 345,
Issue. 12,
p.
113024.
Lin, Hao
Wang, Guanghui
and
Zhou, Wenling
2022.
Integer colorings with no rainbow k-term arithmetic progression.
European Journal of Combinatorics,
Vol. 104,
Issue. ,
p.
103547.
Pikhurko, Oleg
and
Staden, Katherine
2023.
Stability for the Erdős-Rothschild problem.
Forum of Mathematics, Sigma,
Vol. 11,
Issue. ,
BUCIĆ, MATIJA
JANZER, OLIVER
and
SUDAKOV, BENNY
2023.
Counting H-free orientations of graphs.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 174,
Issue. 1,
p.
79.
Conlon, David
Fox, Jacob
He, Xiaoyu
Mubayi, Dhruv
Suk, Andrew
and
Verstraëte, Jacques
2024.
Set-Coloring Ramsey Numbers via Codes.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 61,
Issue. 1,
p.
1.
Pikhurko, Oleg
and
Staden, Katherine
2024.
Exact solutions to the Erdős-Rothschild problem.
Forum of Mathematics, Sigma,
Vol. 12,
Issue. ,
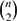 ${n\choose 2}$ as n tends to infinity. Our final result is a stability theorem for complete multipartite graphs G, describing the asymptotic structure of such G with F(G;k) = F(n;k) · 2o(n2) in terms of solutions to the optimisation problem.
${n\choose 2}$ as n tends to infinity. Our final result is a stability theorem for complete multipartite graphs G, describing the asymptotic structure of such G with F(G;k) = F(n;k) · 2o(n2) in terms of solutions to the optimisation problem.