Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-15T01:42:11.494Z Has data issue: false hasContentIssue false
  • English
  • Français

On the K-theory of the extended power construction

Published online by Cambridge University Press:  24 October 2008

J. E. McClure  and
V. P. Snaith
J. E. McClure
Affiliation:
Johns Hopkins University, University of Western Ontario
V. P. Snaith
Affiliation:
Johns Hopkins University, University of Western Ontario
Get access Rights & Permissions [Opens in a new window]

Extract

The construction of Dyer-Lashof operations in K-theory outlined in (6) and refined in (12) depends in an essential way on the descriptions of the mod-p K-theory of EZp, ×ZpXp and EΣ ×σ p Xp given there. Unfortunately, these descriptions are incorrect when p is odd except in the case where the Bockstein β is identically zero in K*(X; Zp), and even in this case the methods of proof used in (6) and (12) are not strong enough to show that the answer given there is correct. In this paper we repair this difficulty, obtaining a complete corrected description of K*(EZp ×ZpXp; Zp) and K*(EΣp) (theorem 3·1 below, which should be compared with ((12); theorems 3·8 and 3·9) and ((6); theorem 3)). Because of the error, the method used in (6) and (12) to construct Dyer-Lashof operations fails to go through for odd primes when non-zero Bocksteins occur, and it is not clear that this method can be repaired. We shall not deal with the construction of Dyer-Lashof operations in this paper. Instead, the first author will give a complete treatment of these operations in (5), using our present results and the theory of H∞-ring spectra to obtain strengthened versions of the results originally claimed in ((12); theorem 5·1). There is also a minor error in the mod-2 results of (12) (namely, the second formula in (12), theorem 3·8 (a) (ii)) should read

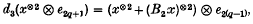
where B2 is the second mod-2 Bockstein, and a similar change is necessary in the second formula of ((12), theorem 3·8(b) (ii)). The correction of this error requires the methods of (5) and will not be dealt with here; fortunately, the mod-2 calculations of ((12), §6–9), (10) and (11) are unaffected and remain true as stated.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 92 , Issue 2 , September 1982 , pp. 263 - 274
Copyright
Copyright © Cambridge Philosophical Society 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Adams, J. F.Stable homotopy and generalized homology (University of Chicago Press, 1974).Google Scholar
(2)Araki, S. and Toda, H.Multiplicative structures in mod-q cohomology theories. I: Osaka Journal of Mathematics 2 (1965), 71–115.Google Scholar
Araki, S. and Toda, H.Multiplicative structures in mod-q cohomology theories. III: Osaka Journal of Mathematics 3 (1966), 81–120.Google Scholar
(3)Atiyah, M. F.Characters and cohomology of finite groups. Publ. Math. IHES 9 (1961), 23–64.CrossRefGoogle Scholar
(4)Atiyah, M. F. and Tall, D. O.Group representations, λ-rings and the J-homomorphism. Topology 8 (1969), 253–297.CrossRefGoogle Scholar
(5)Bruner, B., Lewis, L. G., May, J. P., McClure, J. E. and Steinberger, M.H ∞ ring spectra and their applications. To appear in Lecture Notes in Mathematics (Springer).Google Scholar
(6)Hodgkin, L.Dyer-Lashof operations in K-theory. London Math. Society Lecture Notes 11 (1974), 27–32.Google Scholar
(7)Maunder, C. R. F.Stable operations in mod-p K-theory. Proc. Camb. Phil. Soc. 63 (1967), 631–646.CrossRefGoogle Scholar
(8)May, J. P.A general algebraic approach to Steenrod operations. Lecture Notes in Mathematics, no. 168 (Springer, 1970), pp. 153–231.Google Scholar
(9)May, J. P.H ∞ ring spectra and their applications. Proc. Symp. Pure Math., no. 32 (American Mathematical Society, 1978), part 2, pp. 229–244.CrossRefGoogle Scholar
(10)Miller, H. and Snaith, V. P.On the K-theory of the Kahn-Priddy map. J. London Math. Soc. (2) 20 (1979), 339–342.CrossRefGoogle Scholar
(11)Miller, H. and Snaith, V. P. On K *(QRPn; Z 2). (To appear.)Google Scholar
(12)Snaith, V. P. Dyer-Lashof operations in K-theory. Lecture Notes in Mathematics, no. 496 (Springer, 1975), pp. 103–294.Google Scholar
(13)Hodgkin, L.On the K-theory of Lie groups. Topology 6 (1967), 1–36.CrossRefGoogle Scholar
(14)Nishida, G.Cohomology operations in iterated loop spaces. Proc. Japan Acad. 44 (1968), 104–109.Google Scholar