No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Reade[10] has recently improved Weyl's classical estimate λn = o(n−3/2) for the eigenvalues of a symmetric kernel K∈C1 by relaxing the Cl hypothesis to the assumptions that K∈L2[0, 2π]2, that K is absolutely continuous in each variable separately, and that both ∂K/∂s and ∂K/t belong to L2[0, 2π]2. The conclusion of his theorem, that 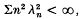 is, of course, stronger than λn = o(n−3/2).
is, of course, stronger than λn = o(n−3/2).