Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kirby, D.
1982.
Subrings of the first neighbourhood ring: II.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 92,
Issue. 1,
p.
35.


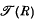 of ideals
of ideals 