No CrossRef data available.
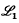 -group
-groupPublished online by Cambridge University Press: 24 October 2008
Let 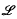 be the class of groups possessing a subgroup of index n for each divisor n of the group order. McLain (7) initiated the formal investigation of
be the class of groups possessing a subgroup of index n for each divisor n of the group order. McLain (7) initiated the formal investigation of 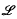 and observed that every solvable group is a direct factor of an
and observed that every solvable group is a direct factor of an 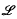 -group. However, subclasses of
-group. However, subclasses of 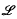 provide some interesting problems. Various subclasses of
provide some interesting problems. Various subclasses of 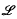 which satisfy other properties were studied by McLain; the upshot being that these classes approach supersolvability. This program was pursued by Humphreys (3) and Humphreys and Johnson (4), among others. In particular,
which satisfy other properties were studied by McLain; the upshot being that these classes approach supersolvability. This program was pursued by Humphreys (3) and Humphreys and Johnson (4), among others. In particular, 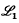 , the largest quotient closed subclass of
, the largest quotient closed subclass of 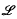 , was considered in (3) and (4). Humphreys (3) has shown an odd order
, was considered in (3) and (4). Humphreys (3) has shown an odd order 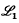 -group is supersolvable, but provides some non-supersolvable
-group is supersolvable, but provides some non-supersolvable 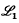 groups. Our motivation is that if S ∈ QR0(S3), the formation generated by S3, and V is a faithful irreducible GF(2) [S]-module, the semidirect product VS ∈
groups. Our motivation is that if S ∈ QR0(S3), the formation generated by S3, and V is a faithful irreducible GF(2) [S]-module, the semidirect product VS ∈ 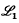 .
.