Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Han-lin
Chui, Charles K.
and
Micchelli, Charles A.
1989.
Multivariate Approximation Theory IV.
p.
73.


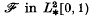 , the space of
, the space of 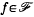 give optimal information for approximation? To make this question precise, we introduce the quantity
give optimal information for approximation? To make this question precise, we introduce the quantity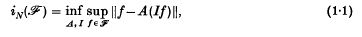
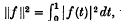 , where
, where 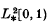 and
and 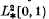 into ℝ
into ℝ