Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mattila, Pertti
2014.
Geometry and Analysis of Fractals.
Vol. 88,
Issue. ,
p.
283.
Orponen, Tuomas
2015.
Hausdorff dimension estimates for restricted families of projections in R3.
Advances in Mathematics,
Vol. 275,
Issue. ,
p.
147.
Dąbrowski, Damian
Orponen, Tuomas
and
Villa, Michele
2022.
Integrability of orthogonal projections, and applications to Furstenberg sets.
Advances in Mathematics,
Vol. 407,
Issue. ,
p.
108567.
Héra, Kornélia
Keleti, Tamás
and
Máthé, András
2024.
A Fubini-type theorem for Hausdorff dimension.
Journal d'Analyse Mathématique,
Vol. 152,
Issue. 2,
p.
471.


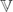 =
= 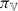 : ℝ
: ℝ