Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Levine, Howard Allen
1970.
On a theorem of Knops and Payne in dynamical linear thermo-elasticity.
Archive for Rational Mechanics and Analysis,
Vol. 38,
Issue. 4,
p.
290.
Horgan, Cornelius O.
1972.
A note on the displacement boundary-value problem of linearized elastodynamics.
Journal of Elasticity,
Vol. 2,
Issue. 4,
p.
357.
Murray, Amy C.
1972.
Uniqueness and continuous dependence for the equations of elastodynamics without strain energy function.
Archive for Rational Mechanics and Analysis,
Vol. 47,
Issue. 3,
p.
195.
Knops, R. J.
and
Wilkes, E. W.
1973.
Mechanics of Solids.
p.
125.
Knops, R. J.
1973.
Symposium on Non-Well-Posed Problems and Logarithmic Convexity.
Vol. 316,
Issue. ,
p.
31.
Hills, R. N.
1973.
On the stability of a linear dipolar fluid.
Acta Mechanica,
Vol. 17,
Issue. 3-4,
p.
255.
Payne, L. E.
1973.
Symposium on Non-Well-Posed Problems and Logarithmic Convexity.
Vol. 316,
Issue. ,
p.
1.
Bloom, Frederick
1975.
On continuous dependence for a class of dynamical problems in linear thermoelasticity.
ZAMP Zeitschrift für angewandte Mathematik und Physik,
Vol. 26,
Issue. 5,
p.
569.
Bloom, Frederick
1976.
On bounds for solutions to nonlinear wave equations in Hilbert space with applications to nonlinear elastodynamics.
Zeitschrift für angewandte Mathematik und Physik ZAMP,
Vol. 27,
Issue. 6,
p.
853.
Beevers, C. E.
1976.
Some stability results in the linear theory of anisotropic elastodynamics.
Journal of Elasticity,
Vol. 6,
Issue. 4,
p.
419.
Leslie, A. S.
1976.
Idealized Optical Fibre Mode Conversion (R. W. Allen).
SIAM Review,
Vol. 18,
Issue. 2,
p.
298.
Beevers, C. E.
and
Engelbrecht, J.
1977.
Energy arguments in linear thermoelasticity.
Acta Mechanica,
Vol. 28,
Issue. 1-4,
p.
201.
Hughes, Thomas J. R.
Kato, Tosio
and
Marsden, Jerrold E.
1977.
Well-posed quasi-linear second-order hyperbolic systems with applications to nonlinear elastodynamics and general relativity.
Archive for Rational Mechanics and Analysis,
Vol. 63,
Issue. 3,
p.
273.
Hughes, Thomas J. R.
and
Marsden, Jerrold E.
1978.
Classical elastodynamics as a linear symmetric hyperbolic system.
Journal of Elasticity,
Vol. 8,
Issue. 1,
p.
97.
Chiritǎ, S.
1982.
UNIQUENESS AND CONTINUOUS DEPENDENCE RESULTS FOR THE INCREMENTAL THERMOELASTICITY.
Journal of Thermal Stresses,
Vol. 5,
Issue. 2,
p.
161.
Galdi, Giovanni P.
and
Rionero, Salvatore
1983.
Continuous data dependence in linear elastodynamics on unbounded domains without definiteness conditions on the elasticities.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 93,
Issue. 3-4,
p.
299.
Crooke, P. S.
and
Payne, L. E.
1984.
Continuous dependence on geometry for the backward heat equation.
Mathematical Methods in the Applied Sciences,
Vol. 6,
Issue. 1,
p.
433.
Payne, L.E.
1987.
Inverse and Ill-Posed Problems.
p.
399.
Knops, R. J.
1987.
Existence of weak solutions to linear indefinite systems of differential equations.
Archive for Rational Mechanics and Analysis,
Vol. 98,
Issue. 2,
p.
179.
Knops, R. J.
1987.
Analysis and Thermomechanics.
p.
525.
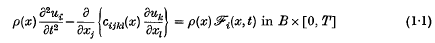
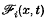 i(x, t) are the Cartesian components of body force per unit mass, and cijkl(x) are the non-homogeneous elasticities, which apart from certain smoothness conditions stated later, are assumed to possess the symmetry
i(x, t) are the Cartesian components of body force per unit mass, and cijkl(x) are the non-homogeneous elasticities, which apart from certain smoothness conditions stated later, are assumed to possess the symmetry