No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let {Xi. i ≥1} be a sequence of independent exponential random variables with mean 1. Setting S(n) = X1 +…+ Xn, S(0) = 0, we define
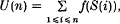
where f is a real-valued, measurable function satisfying
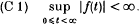 .
.