Published online by Cambridge University Press: 24 October 2008
Let Kr denote the set of r-tuples n = (n1, n2, …, nr), r ≥ 1, where the components ni are positive integers. Let {X, Xn, n ∈ Kr} be a family of independent and identically distributed random variables with positive mean EX = μ < + ∞ and finite variance VX = σ2 < + ∞. In a recent work, M. Maejima and T. Mori [2] have shown that, if X is integer valued, aperiodic and E∣X∣3 < + ∞, then, for r = 2 or 3,
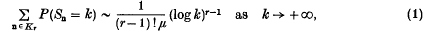
where

the summation being extended over all members j = (j1,j2, …, jr) of Kr that satisfy jt ≤ nt for all 1 ≤ t ≤ r.