Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Naylor, D.
Choo, F. C.
and
Barclay, D. W.
1973.
On an eigenfunction expansion associated with a condition of radiation. II.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 74,
Issue. 3,
p.
485.
Naylor, D.
1975.
On an integral transform associated with a condition of radiation, part 2.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 77,
Issue. 1,
p.
189.
Naylor, D.
1978.
On a Nonself Adjoint Eigenfunction Expansion.
SIAM Journal on Mathematical Analysis,
Vol. 9,
Issue. 5,
p.
967.
Naylor, D.
1979.
On an integral transform.
Glasgow Mathematical Journal,
Vol. 20,
Issue. 1,
p.
1.
Sundar, R.S
Kutty, T.R.G
and
Sastry, D.H
2000.
Hot hardness and creep of Fe3Al-based alloys.
Intermetallics,
Vol. 8,
Issue. 4,
p.
427.


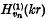 where υ
where υ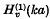 regarded as a function of its order. Here
regarded as a function of its order. Here