Published online by Cambridge University Press: 24 October 2008
In this paper we calculate part of the integral cohomology ring of the sporadic simple group J4; this group has order 221.33.5.7. 113.23.29.31.37.43. More precisely, we obtain all of the cohomology ring except for the 2-primary part. As the cohomology has already been written down [9] at the primes which divide the group order only once, we concentrate here on the primes 3 and 11. In both of these cases the Sylow p-subgroups are extraspecial of order p3 and exponent p. We use the method which identifies the p-primary cohomology with the ring of stable classes in the cohomology of a Sylow p-subgroup. The stable classes are all invariant under the action of the Sylow p-normalizer; and some time is spent finding invariant classes in the cohomology ring of 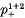 , the extraspecial group. Section 2 studies the prime 11: the invariant classes are the stable classes, because the Sylow 11-subgroups have the Trivial Intersection (T.I.) property. In Section 3 we study the prime 3, and see that all conditions for invariant classes to be stable reduce to one condition.
, the extraspecial group. Section 2 studies the prime 11: the invariant classes are the stable classes, because the Sylow 11-subgroups have the Trivial Intersection (T.I.) property. In Section 3 we study the prime 3, and see that all conditions for invariant classes to be stable reduce to one condition.