Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Riley, Robert
1975.
Discrete parabolic representations of link groups.
Mathematika,
Vol. 22,
Issue. 2,
p.
141.
Harvey, William James
1978.
Séminaire Bourbaki vol. 1976/77 Exposés 489–506.
Vol. 677,
Issue. ,
p.
30.
Riley, Robert
1979.
Topology of Low-Dimensional Manifolds.
Vol. 722,
Issue. ,
p.
99.
Schwermer, Joachim
1980.
A note on link complements and arithmetic groups.
Mathematische Annalen,
Vol. 249,
Issue. 2,
p.
107.
Magnus, W.
1981.
The uses of 2 by 2 matrices in combinatorial group theory. A survey.
Results in Mathematics,
Vol. 4,
Issue. 1-2,
p.
171.
Grunewald, Fritz
and
Schwermer, Joachim
1981.
A nonvanishing theorem for the cuspidal cohomology of SL2 over imaginary quadratic integers.
Mathematische Annalen,
Vol. 258,
Issue. 2,
p.
183.
Grunewald, Fritz J.
and
Schwermer, Joachim
1981.
Arithmetic quotients of hyperbolic 3-space, cusp forms and link complements.
Duke Mathematical Journal,
Vol. 48,
Issue. 2,
Milnor, John W.
1982.
Hyperbolic geometry: The first 150 years.
Bulletin of the American Mathematical Society,
Vol. 6,
Issue. 1,
p.
9.
Brooks , Robert
and
Matelski, J. Peter
1982.
Collars in Kleinian groups.
Duke Mathematical Journal,
Vol. 49,
Issue. 1,
Schwermer, Joachim
and
Vogtmann, Karen
1983.
The integral homology ofSL 2 andPSL 2 of euclidean imaginary quadratic integers.
Commentarii Mathematici Helvetici,
Vol. 58,
Issue. 1,
p.
573.
Riley, Robert
1983.
Applications of a computer implementation of Poincaré’s theorem on fundamental polyhedra.
Mathematics of Computation,
Vol. 40,
Issue. 162,
p.
607.
Wagoner, J. B.
1984.
A 𝑝-adic regulator problem in algebraic 𝐾-theory and group cohomology.
Bulletin of the American Mathematical Society,
Vol. 10,
Issue. 1,
p.
101.
Lee, Youn W.
1985.
Abelian rank of normal torsion-free finite index subgroups of polyhedral groups.
Transactions of the American Mathematical Society,
Vol. 290,
Issue. 2,
p.
735.
Nicas, Andrew J.
1986.
An infinite family of non-Haken hyperbolic 3-manifolds with vanishing Whitehead groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 99,
Issue. 2,
p.
239.
Tsau, Chichen M.
1986.
Algebraic meridians of knot groups.
Transactions of the American Mathematical Society,
Vol. 294,
Issue. 2,
p.
733.
Chinburg, Ted
1987.
A small arithmetic hyperbolic three-manifold.
Proceedings of the American Mathematical Society,
Vol. 100,
Issue. 1,
p.
140.
Humphries, S. P.
and
Long, D. D.
1987.
On the Mal'cev quotients of certain hyperbolic link groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 102,
Issue. 3,
p.
475.
Baker, Mark D.
1988.
The virtual 𝑍-representability of certain 3-manifold groups.
Proceedings of the American Mathematical Society,
Vol. 103,
Issue. 3,
p.
996.
Lee, Youn W.
1989.
On normal torsion-free finite index subgroups of polyhedral groups.
Topology and its Applications,
Vol. 32,
Issue. 1,
p.
25.
Reid, Alan W.
1991.
Totally geodesic surfaces in hyperbolic 3-manifolds.
Proceedings of the Edinburgh Mathematical Society,
Vol. 34,
Issue. 1,
p.
77.
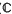 ): = PSL(2,
): = PSL(2, 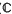 ). The most obvious problem that this suggests is the determination of a presentation for an image group πKθ. We shall settle the easiest outstanding case in section 2 below, viz. k the figure-eight knot 41, which has the 2-bridge normal form (5, 3). We shall prove that the (two equivalent) p-reps θ for this knot are isomorphisms of πK on πKθ. Furthermore, the universal covering space of S3\k can be realized as Poincaré's upper half space
). The most obvious problem that this suggests is the determination of a presentation for an image group πKθ. We shall settle the easiest outstanding case in section 2 below, viz. k the figure-eight knot 41, which has the 2-bridge normal form (5, 3). We shall prove that the (two equivalent) p-reps θ for this knot are isomorphisms of πK on πKθ. Furthermore, the universal covering space of S3\k can be realized as Poincaré's upper half space 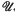 3, and πKθ is a group of hyperbolic isometries of
3, and πKθ is a group of hyperbolic isometries of 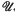 3 which is also the deck transformation group of the covering
3 which is also the deck transformation group of the covering 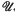 3 → S3\k. The group πKθ is a subgroup of two closely related groups that we study in section 3. We shall give fundamental domains, presentations, and other information for all these groups.
3 → S3\k. The group πKθ is a subgroup of two closely related groups that we study in section 3. We shall give fundamental domains, presentations, and other information for all these groups.