No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let G be a metrizable non-discrete locally compact group. Let M(G) be the convolution measure algebra of G. We shall denote by Lx and Rx, x β G, the left and the right translation operation on M(G), respectively. A measure μ β M(G) has strongly independent powers or μ is a s.i.p. measure, if, for x β G and n, m β N,
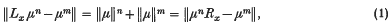
whenever n ≠ m or x ≠ e, where e is the identity of G. If a measure μ satisfies (1) for x = e and n + m, we say that μ has independent powers, or μ is an i.p. measure. Notice that the powers μn and μm of μ are convolution powers.